一类两阶段肿瘤-免疫模型的确定性与随机分析*

李孟阳 李伟 黄冬梅 杨贵东

（西安电子科技大学数学与统计学院，西安 710071）

引言

癌症作为一种恶性肿瘤，正严重威胁人类的健康.根据国际癌症研究机构（IARC）发布的《全球癌症研究报告》，2018年全球新增癌症病例近1800万，且致死率正在逐年增加[1].众所周知，尽管临床上对癌症可以进行手术、放疗、化疗等治疗，但不可预期的复发和再次扩散，使得攻克癌症依然是目前医学上最大的难题之一.而生物实验需要大量的人力、物力、实验设备和实验技术，各种局限性使得生物数学模型以及机理分析极其重要，成为不可或缺的用来理解肿瘤发生、演化和扩散的重要工具[2].

免疫系统是人体自我保护的重要组织之一，具有识别和消灭恶性肿瘤的功能[3].一般来说，如果肿瘤细胞在某一组织中产生，人体对肿瘤的免疫反应就会被激活，同时，效应细胞等多种免疫细胞会刺激淋巴细胞在肿瘤表面进行分裂、协调，并放置抗体来防御肿瘤.

目前关于肿瘤-免疫系统相互作用的模型[4-10]主要有两类.一类是根据肿瘤细胞的生化反应特征，建立确定性动力学模型，集中讨论肿瘤免疫系统解的存在性、稳定性、参数估计和分岔等[11-16].另一类是考虑细胞生长的内外微环境，将随机因素引起的随机涨落模型化为噪声，建立随机动力学模型，讨论随机因素对肿瘤发生、发展以及消亡的影响[17-23].

不同类型的模型作用不同，对理解肿瘤与免疫系统之间的竞争都各有帮助.相对确定性模型而言，随机肿瘤-免疫模型的动力学讨论文献积累比较少，变量主要局限于一维或二维情形.这是因为随机项和非线性项的引入，增加了随机肿瘤-免疫模型的理论与数值求解的难度，特别是噪声的存在，其分布类型更是直接关系到随机肿瘤-免疫模型是否能够求解.然而，在肿瘤与免疫系统的斗争中，对肿瘤具有抑制作用的效应细胞通常有多种，如巨噬细胞、细胞毒性T细胞、NK细胞等，它们与肿瘤细胞之间的相互作用也极其复杂，三维及更高维的随机肿瘤-免疫模型才更符合实际的肿瘤-免疫关系.

基于淋巴细胞在免疫应答中的生化特点以及肿瘤免疫实验结果，DeLisi等[26]提出：只有发育成熟的淋巴细胞才能有效杀死肿瘤细胞，免疫系统对肿瘤的消除应该对淋巴细胞按成熟与未成熟两阶段分别进行考虑.之后，Liu等[27]对这一见解给予了肯定，并在文献[26]的基础上对两阶段确定性肿瘤-免疫模型的退化平衡点进行了定性分岔分析.再后，庞留勇等[28]对该模型进行了简化，重点从理论上研究了Hopf分岔的条件公式.蒙玉倩等[29]进一步将该模型进行了改进，考虑了在分数阶情形下该确定性肿瘤-免疫模型的稳定性，分析了两阶段淋巴细胞的动态演变情况.

本文将基于文献[26-29]的工作，将淋巴细胞抵御肿瘤的过程分为两个阶段，即被激活的未成熟淋巴细胞的生长阶段和能有效消除肿瘤细胞的成熟淋巴细胞的防御阶段.同时，本文将在这些确定性模型基础上继续深入探讨该模型的相关性质，并将细胞微环境产生的随机涨落也考虑在内，在理论上研究肿瘤细胞、未成熟淋巴细胞以及成熟淋巴细胞之间的三维随机模型，探讨随机涨落对肿瘤生成以及演变过程的影响.

1 确定性肿瘤-免疫模型

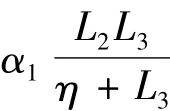
基于上述分析，下面利用Runge-Kutta方法对确定性模型（2）进行数值模拟来验证结论的正确性.假设肿瘤已经生成，淋巴细胞已经被激活并进行防御，可设初始点为 P（1，1，1），若参数值分别为 a=0.9，b=0.6，c=0.6，k=0.8 ，则系统响应将渐进趋近于一个稳定的无肿瘤平衡点E1（0，1，0），如图1所示.说明即使肿瘤细胞的增殖率达到0.8，免疫系统的60%杀死率也足以清除所有的肿瘤细胞，最终病人将被治愈，成为无肿瘤的状态.未成熟的淋巴细胞在发育成熟后，不再被激活.

图 1 E1的相图，取 a=0.9，b=0.6，c=0.6，k=0.8Fig.1 Phase diagram of E1 for a=0.9，b=0.6，c=0.6，k=0.8

对于第二个平衡点E2，与E1的分析过程类似，当参数满足条件：

图2给出了条件（8）下的E2稳定性区域划分.注意到现实中任何时候并不期望肿瘤出现或长期存在，也就意味着E2的稳定性对人类健康没有好处，它的不稳定才会带来治疗与控制的机会.因此，图3考查了初始点为 P（1，1，1）时不同杀死率下的三类细胞演化情况.

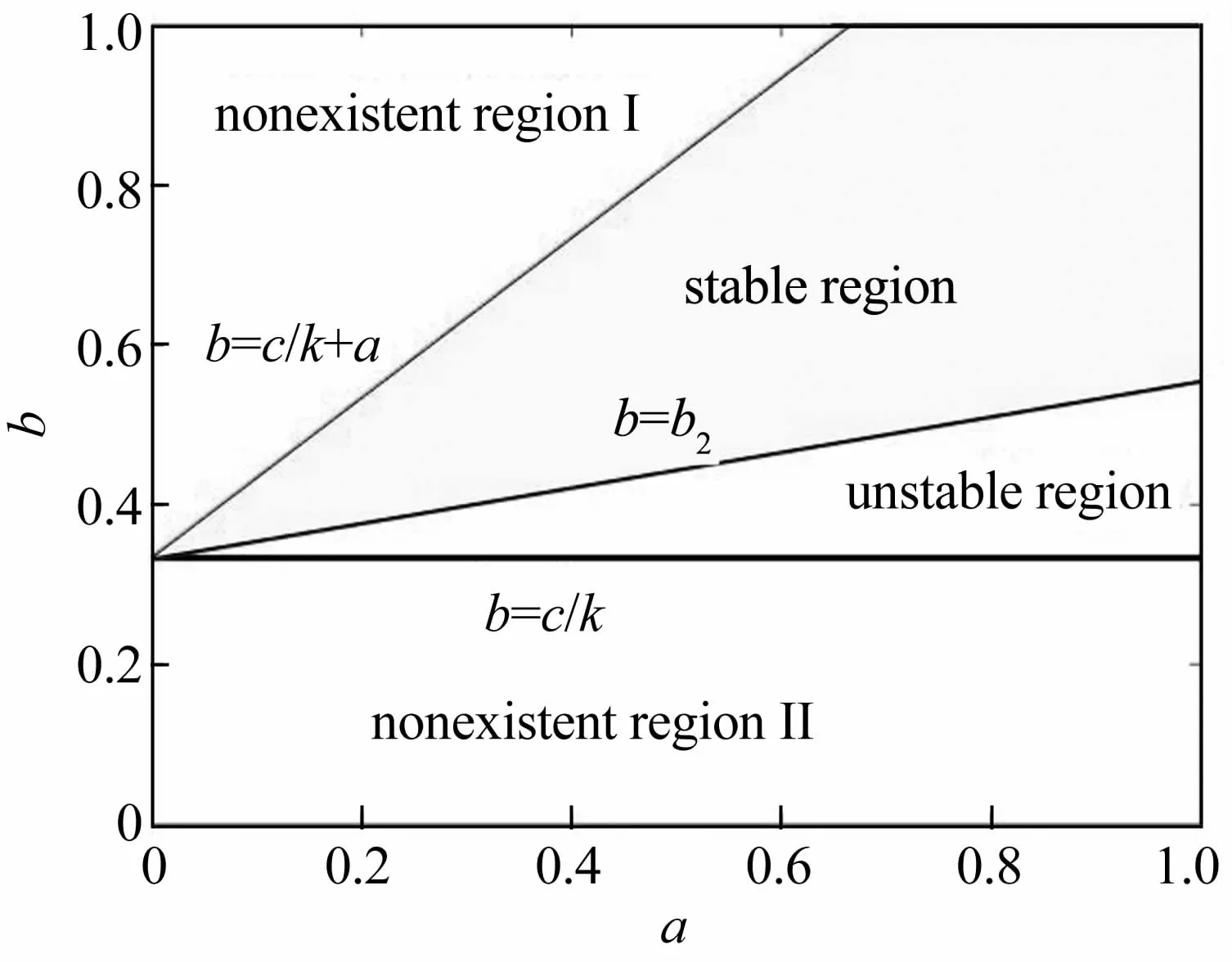
图2 E2的稳定区域，取c=0.2，k=0.6Fig.2 The stable region of E2 for c=0.2，k=0.6

显然，若保持成熟淋巴细胞和肿瘤的增殖率不变，即a=0.9，b=0.6，k=0.8，随着杀死率的逐渐减小，系统（2）从（a）和（b）中的稳定状态转变为（c）中的不稳定状态.此外，（a）中的稳定点逐渐变成一个不稳定的极限环.这说明免疫系统对肿瘤的抵抗能力较弱，不能杀死全部的肿瘤细胞，免疫细胞与肿瘤细胞一直处于此起彼伏的较量之中.图3中z轴为肿瘤细胞密度.可以看到，随着参数c的减小，肿瘤细胞密度不断增加，说明肿瘤细胞一直存在于人体，并正在发展和恶化.

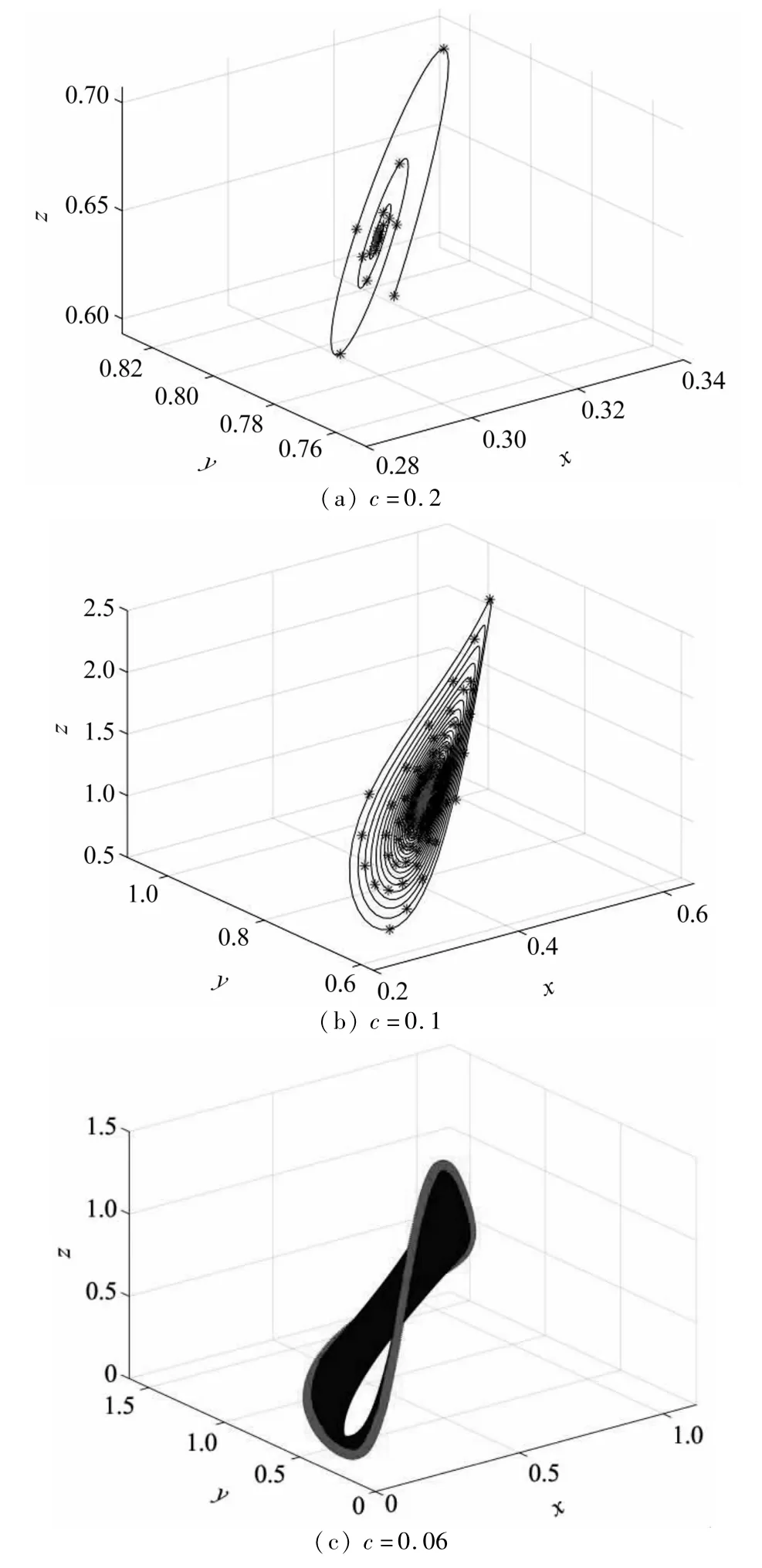
图 3 E2的相图，取 a=0.9，b=0.6，k=0.8Fig.3 Phase diagram of E2 for a=0.9，b=0.6，k=0.8

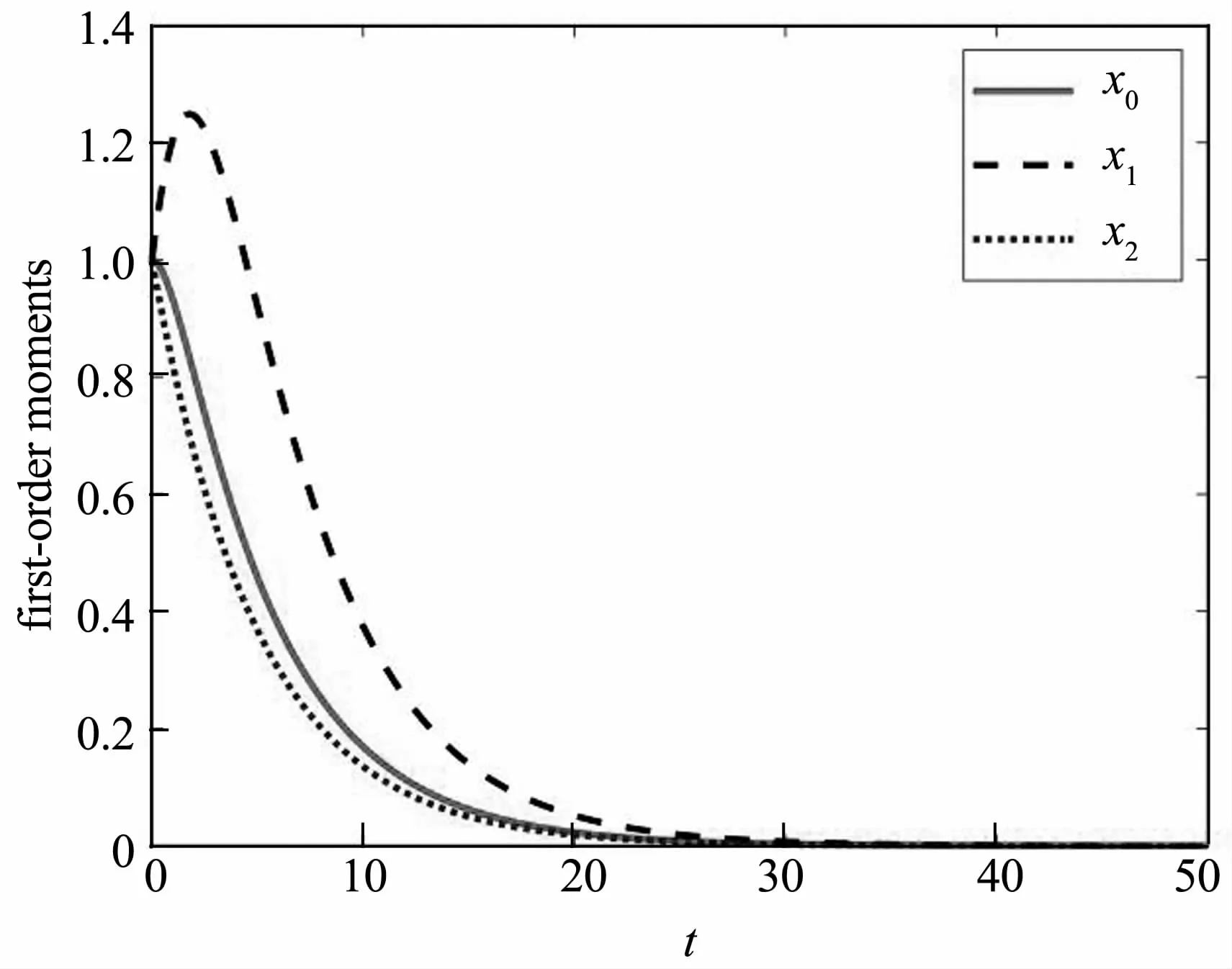
图 4 E1的一阶矩，取 a=0.9，b=0.6，c=0.6，k=0.8Fig.4 The first-order moments of E1 for a=0.9，b=0.6，c=0.6，k=0.8

2 随机肿瘤-免疫模型

细胞生成的内外环境极其复杂，肿瘤细胞和免疫细胞难免也会受到环境随机因素的影响，如外部的化学药剂、温度、供氧量和辐射线等，内部的温度、压力、细胞大小以及细胞浓度等.因此，构建肿瘤-免疫系统模型时不可避免地需要考虑随机噪声[31].按照噪声来源，细胞内微环境形成的随机涨落为加性噪声，而外部因素形成的噪声为乘性噪声.

本节在确定性肿瘤-免疫系统的基础上，将微环境产生的随机扰动模型化为相互独立的高斯白噪声，考虑如下随机情形时的三维肿瘤-免疫系统：

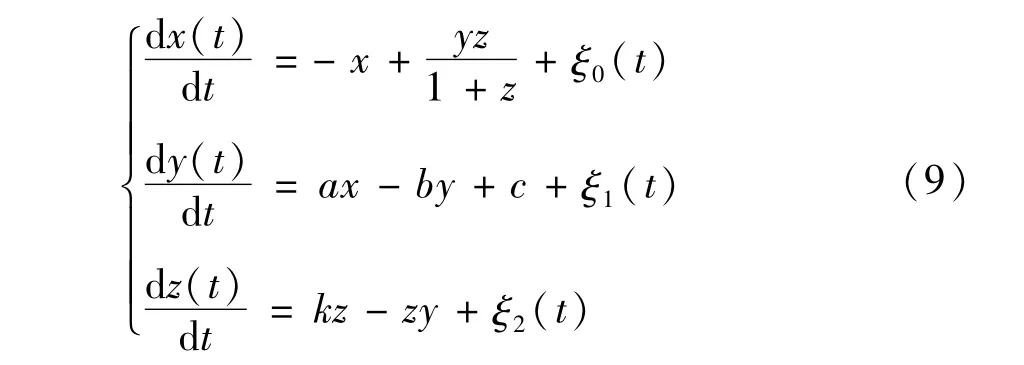
其中，高斯白噪声 ξi（t）（i=0，1，2） 满足均值函数为 〈ξi（t）〉 =0 ， 相关函数为 〈ξi（t）ξi（t′）〉 =2Diiδ（t-t′） ，这里 Dii为 ξi（t） 的噪声强度.

显然，随机噪声的存在，使得三类细胞密度在时间的演化过程中也具有随机性，只能通过概率统计的方法确定它们的性质和规律.另外，由于随机性的存在，本文将主要关注确定性系统中的两个平衡态，观察平衡态附近细胞密度的随机涨落.

2.1 统计分析

这是一个三维的确定性偏微分方程，描述了三类细胞在空间中的联合概率分布情况.无论是瞬态解还是稳态解，方程（11）的求解一般来说都是相当困难的.下面将主要讨论细胞变量的统计矩.

文献[32]已经证明，系统变量xi及其导数的统计矩可以分别利用FP方程计算得出，即

均值函数以 P（1，1，1）为初始值的解曲线如图4所示.图中可以看出，未成熟免疫细胞与肿瘤细胞在有肿瘤的初始条件下随时间单调递减到0，但成熟免疫细胞先增后减并随时间逐渐减小到0.显然在拐点前，未成熟的淋巴细胞逐渐成熟，加入抵御肿瘤细胞的大军，成熟细胞数量增加是必然的.然而在拐点后，单调的减少与确定性情形截然不同，没有渐近趋于数值1.说明噪声即微环境改变了成熟淋巴细胞原有的演变规律，说明此处微环境有利于肿瘤的生存和生长.成熟的免疫细胞在微环境作用下逐渐死亡并退出防御系统.

考虑细胞变量的二阶矩，取n=2，则得到一个关于细胞密度方差和协方差的6个常微分方程：

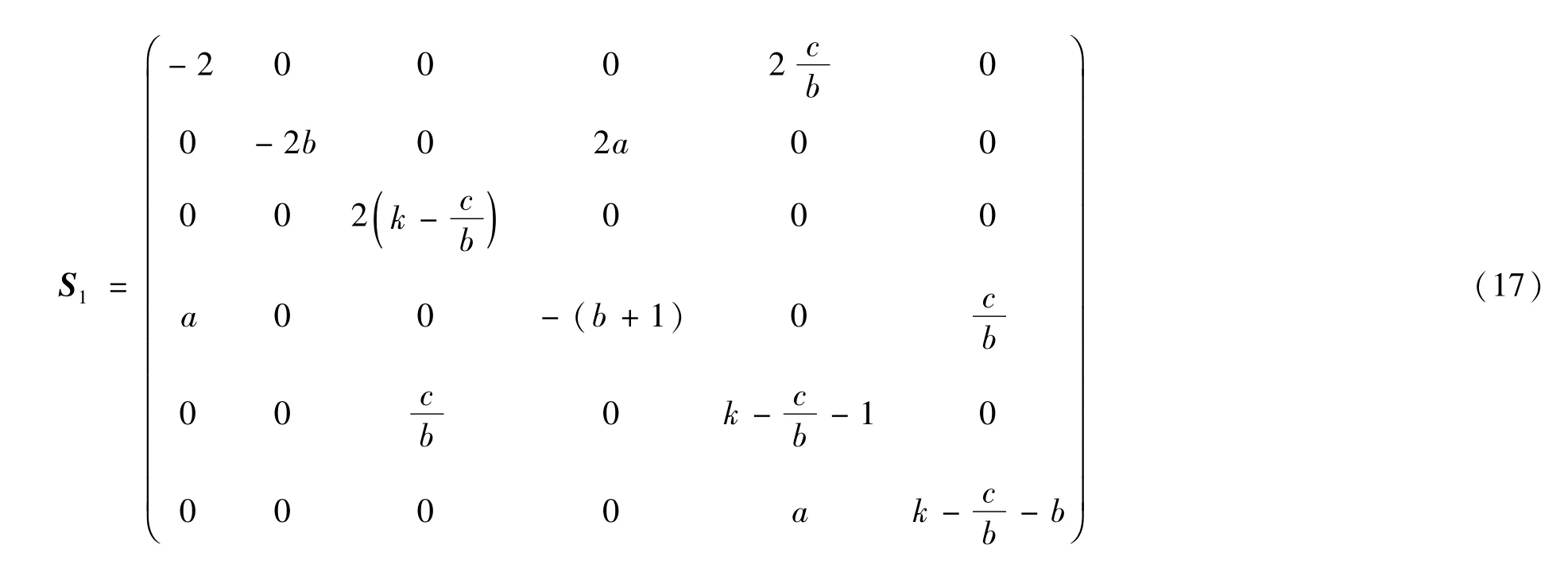
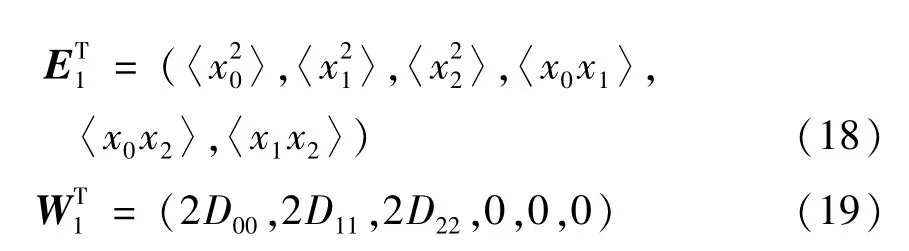
求解该方程组，则细胞密度 xi（i=0，1，2） 的方差和协方差如图5所示.

图5 不同噪声强度D22时E1的二阶矩.a=0.9，b=0.6，c=0.6，k=0.8，D00=0.001，D11=0.001Fig.5 The second-order moments of E1 with different noise intensities D22.a=0.9，b=0.6，c=0.6，k=0.8，D00=0.001，D11=0.001

图5给出了三种细胞的六个二阶矩在肿瘤细胞微环境噪声强度下的时间演变情况.可以看出，当噪声强度较小时，比较而言，成熟的淋巴细胞前期波动较大，但随着肿瘤-免疫系统的不断演化，三类细胞的数量波动逐渐减缓，趋于平缓到一个较小的值.然而，当肿瘤细胞微环境的噪声强度较大时，三类细胞波动不断持续增大，肿瘤与免疫细胞之间的斗争更加激烈，并始终保持较大的数值.说明微环境此时严重影响细胞间的演变，肿瘤与免疫系统间的竞争此起彼伏，一直处于胶着的状态.

均值函数解曲线如图6所示.参数值相同时，三种细胞的均值函数前期呈现出较大的振荡，随着时间的增加最终趋于0.其中，肿瘤细胞受微环境影响产生的振幅较大，它更易受到微环境的干扰.

图 6 E2的一阶矩，取 a=0.9，b=0.6，c=0.2，k=0.8Fig.6 The first-order moments of E2 for a=0.9，b=0.6，c=0.2，k=0.8

将方程（21）代入式（13）得到变量 yi（i=0，1，2）的6个二阶矩的微分方程组：

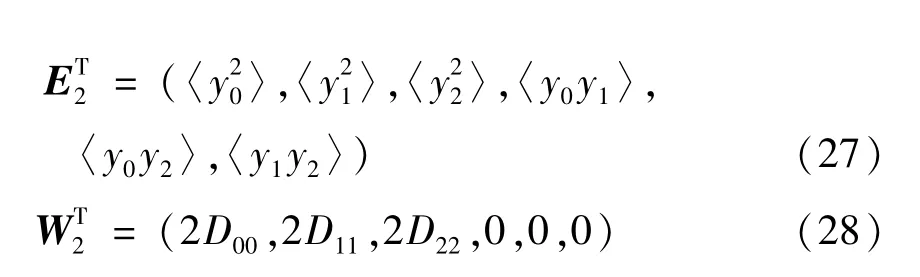
图7给出了E2附近的二阶矩随噪声强度的变化.这里出现一个非常有趣的结果，即肿瘤细胞无论噪声强度大小，始终呈现出很大的波动，而免疫细胞几乎没有波动.这种情况说明，在肿瘤一直存在的状态下，细胞与免疫细胞长期处于竞争状态，微环境对细胞间的演变影响较小.

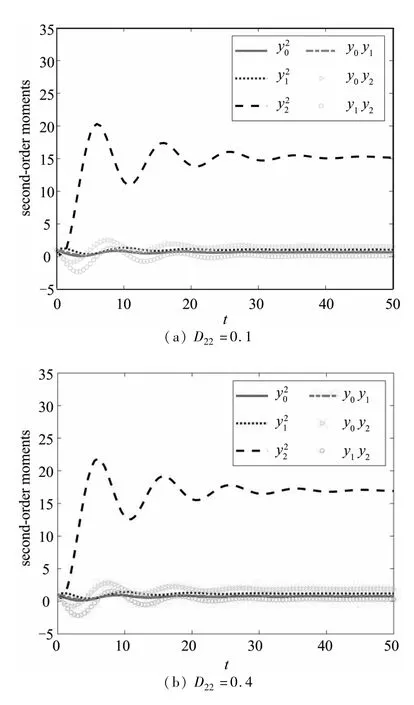
图 7 E2的二阶矩，取 a=0.9，b=0.6，c=0.08，k=0.8，D00=0.001，D11=0.001Fig.7 The second-order moments of E2 for a=0.9，b=0.6，c=0.08，k=0.8，D00=0.001，D11=0.001

注意到当 bk-c=0时，平衡点 E2（x2*，y2*，z2*）的x2*与z2*均变为0.此时，未成熟的免疫细胞与肿瘤细胞都不存在，平衡点E2可转化为E1.因此，接下来主要研究有肿瘤平衡点E2的有关性质.

2.2 敏感性分析

显然，免疫系统对肿瘤细胞的杀死率、肿瘤细胞的自我增殖率来说都是十分重要的参数，它们的取值将直接影响到肿瘤是否能够得到控制.因此这部分将引入敏感系数的概念，来讨论肿瘤-免疫系统中各类细胞的稳态值对参数取值的敏感依赖性.敏感系数定义如下：

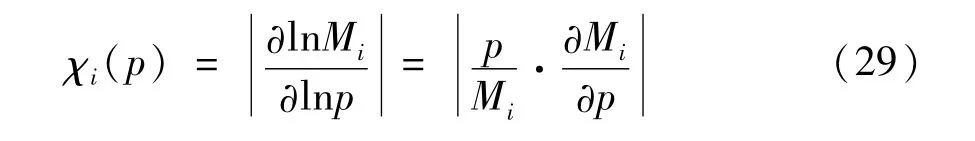
其中，Mi（i=0，1，2） 表示肿瘤 -免疫系统中第 i种细胞的稳态值，p表示系统中某参数.

在肿瘤与免疫系统的竞争关系中，成熟淋巴细胞的杀死率大小是一个至关重要的参数，决定了免疫系统是否能够有效清除肿瘤细胞，并控制肿瘤的发展和扩散.因此，这里主要考查杀死率参数c对第二个稳态值E2的影响，即M0=x*2，M1=y*2，M2=z*2.由公式（29）有

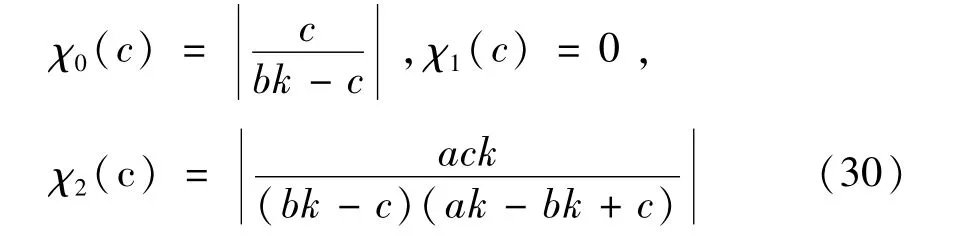
因此，图8给出了第二个稳态值E2附近三种细胞表型对杀死率的敏感性曲线.可以看出，当参数a，b，k固定时，随着c的增加，第一阶段免疫细胞和肿瘤细胞都敏感依赖于参数c，并呈非线性增加.第二阶段免疫细胞的敏感系数为0，即对成熟淋巴细胞的密度没有影响.观察敏感系数曲线的发展趋势，不难判断，当杀死率进一步增大时，肿瘤细胞密度和未成熟淋巴细胞的密度将强烈地依赖参数c，因为需要大量的未成熟淋巴细胞转化为具有杀伤力的成熟淋巴细胞，并保持成熟淋巴细胞的恒定，去抵抗肿瘤细胞.这个过程中，免疫细胞与肿瘤细胞在数量上变化较大，故依赖于参数c.

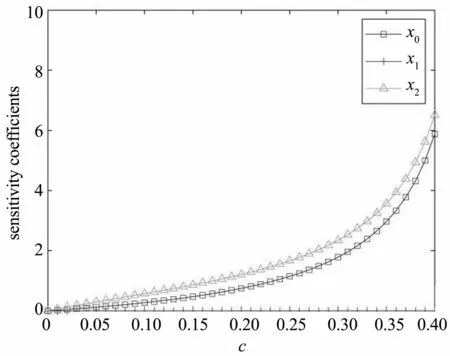
图8 三种细胞表型对杀死率c的敏感性依赖.a=0.9，b=0.6，k=0.78Fig.8 The sensitivity of three cell phenotypes on the parameter of killing rate c.a=0.9，b=0.6，k=0.78

3 结论

本文研究了高斯白噪声作用下的两阶段肿瘤-免疫细胞模型.对确定性模型中稳态解的动力学性质进行了分析和仿真.考虑到细胞微环境对系统的影响，将高斯白噪声引入模型，基于朗之万理论和FP方程给出了随机肿瘤免疫模型细胞的一阶矩和二阶矩方程，并讨论了细胞的方差和敏感系数等性质.研究表明噪声会改变免疫系统对肿瘤细胞的防御规律.当噪声强度较大时，肿瘤细胞更易受到微环境影响，其密度在短时间内发生剧烈变化，肿瘤与免疫细胞之间的斗争更加激烈.敏感系数表明肿瘤细胞对免疫系统的杀死率参数c很敏感.最后通过数值方法，验证了分析结果的准确性.