基于几何积分方法的压电岛-桥结构动力行为分析*

鲁康 王博，4† 毕皓皓 师岩 邓子辰，5†

（1.西北工业大学工程力学系，西安 710072）

（2.西北工业大学 应用数学系，西安 710072）

（3.南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

（4.大连理工大学工业装备结构分析国家重点实验室，大连 116024）

（5.西北工业大学复杂系统动力学与控制工信部重点实验室，西安 710072）

引言

柔性电子器件以其独特的延展性在生物医疗、电子设备和航空航天等领域展现出巨大的应用潜力[1].近年来，柔性电子技术发展迅速，衍生出的基于力学设计的延展柔性结构设计技术[2，3]，既能保持无机电子器件“硬而脆”的电学性能，又使其具备一定的延展性.在可延展柔性结构设计方法中，一种基于岛-桥结构的设计方法能够提升柔性电子器件的延展性至少100%，因而得到学术和工业界的广泛关注[4，5].

岛-桥结构又称非共面网格结构[6]，由刚性功能部件（“岛”）和互联导线（“桥”）共同组成.通常，“岛”和“桥”都粘接在柔性基底上，通过释放基底的预拉伸，“桥”发生面外屈曲，使得刚性功能模块保持在低应变状态，从而实现岛-桥结构的可延展性，图1给出了扫描电子显微镜拍摄的岛-桥阵列和结构示意图[7].针对屈曲岛-桥结构，Zhang等[8]对其屈曲行为展开了研究，他们给出了岛-桥结构屈曲的临界应变解析表达式，并对互联导线的设计进行了优化，提升了其拉伸延展率.压电材料具有优良的力学和电学性能，是作为岛-桥结构互联导线的理想材料[9].Huang[10]团队基于压电材料的蛇形/自相似岛-桥结构，制备出高拉伸性、高稳定性、高灵敏度的类人工皮肤.基于压电薄膜结构，Lin[11]等设计出屈曲梁阵列结构的能量采集器.然而，对于屈曲岛-桥结构的柔性电子器件，无论是在制备过程中[12]，还是在工作过程中[13]，都不可避免地受到外界复杂的温度场、电场等物理场的作用，影响其灵敏性[14].近年来，该类问题得到国内外学者们的广泛关注，郭伟国等[15]研究了温度变化对压电薄膜的压电系数的影响，理论和实验表明：压电薄膜对温度非常敏感.申胜平等[16]研究了温度对压电材料中挠曲电效应的影响，实验表明：温度对压电材料挠曲系数产生非线性影响.李世荣等[17]考虑了温度及电场的耦合作用，研究了压电层合梁的屈曲及后屈曲行为，他们发现：在屈曲和后屈曲阶段，温度对压电梁的低阶固有频率有着显著而不同的影响.Shariyat[18]研究了压电层合结构在温度场、电场以及变形场耦合作用下的动态屈曲行为，结果表明：温度梯度对结构的动态屈曲有显著的影响.

图1 岛-桥结构示意图Fig.1 Diagram of island-bridge structure

对于岛-桥结构的力学行为研究，一般将作为互联导线的压电薄膜等效成Euler-Bernoulli梁来研究.彭剑等[19]针对轴向周期载荷激励下的压电Euler梁，采用多尺度分析方法给出了压电梁的振动稳定域.Nayfeh等[20]基于Euler-Bernoulli梁理论研究了各种边界条件下梁的非线性后屈曲问题，并得到了相应的临界屈曲载荷.Wang和Feng等[21]将屈曲薄膜等效为Euler梁，研究了表面残余应力对屈曲薄膜静态和动态行为的影响.当梁是“短粗梁”时，梁的横截面剪切变形和转动惯量会对其动力学特性产生一定的影响.盛冬发等[22]采用Timoshenko梁理论，分析了具有非线性损伤的粘弹性梁的动力学响应和混沌现象.杨晓东等[23]针对两端铰支的Timoshenko梁，对其横向振动问题展开了研究，给出了其固有频率表达式.周强等[24]基于Timoshenko梁理论，针对压电纳米梁，研究了表面效应对梁振动响应的影响.

本文针对屈曲压电岛-桥结构，采用Timoshenko梁理论建立其振动控制方程.并利用几何积分方法求解相应的动力学方程.分析了温度变化和工作电压对屈曲压电岛-桥结构动力学特性的影响.

1 压电屈曲薄膜的动力学模型

在岛-桥结构柔性电子器件中，屈曲的压电梁结构被用来连接功能模块，如图1（b）所示.两端固支的压电Timoshenko梁如图2（a）所示，其中L为屈曲后长度，b为宽度，h为厚度，ρ为密度，I为面积惯性矩，A为横截面面积.

图2 岛-桥结构力学分析模型Fig.2 Mechanical analysis model of island-bridge structure

鉴于屈曲压电梁结构将发生大变形，梁的横截面剪切变形和转动惯量将会对其力学行为产生一定的影响[26].基于Timoshenko梁理论，压电梁的本构方程为[27，28]，

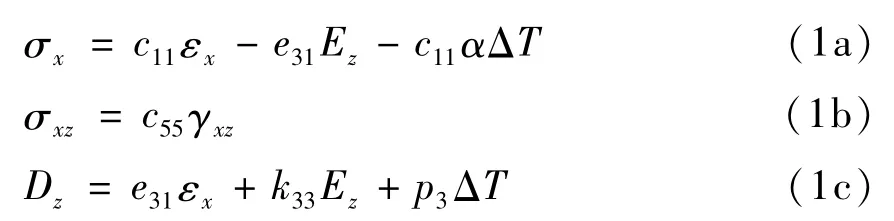
其中，σx，σxz和Dz分别为轴向应力、剪切应力和z方向上的电位移；c11，e31，k33和p3分别表示弹性模量、压电常数、介电常数以及热电常数；c55=κG为修正剪切模量，Ez为z方向上的电场强度，α为轴向热膨胀系数，ΔT为温度变化量.εx为轴向应变，γxz为剪切应变，其表达式如下：

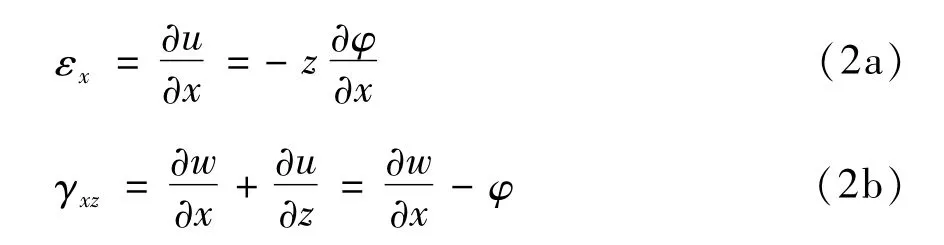
其中，u，w和φ分别表示梁的径向挠度，横向挠度和横截面转角.

由于电场的作用只在z方向上产生应变，故假设只在z方向存在电场，则电场Ez可以由电势Φ确定[28]

2 近似求解

对于偏微分方程（13）无法得到其解析解，Galerkin截断法作为一种简便有效的近似方法，可以将偏微分方程离散为常微分方程.本文采用Galerkin方法[23]分析屈曲压电岛-桥结构的动力学行为.

对于图2描述的压电梁，两端固支边界条件表述为

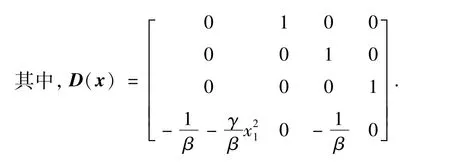
3 Magnus几何积分方法

对于非线性方程（21），无法得到解析解，只能通过数值方法进行求解.本文考虑应用Magnus几何积分方法求解非线性动力学控制方程（21）.Magnus方法几何积分方法在数值计算方面具有显著的优点：即使适当截断，数值结果依然可以保持原动力学问题的几何性质[31].

4 数值算例

4.1 几何积分方法的有效性验证

对于压电岛-桥结构，由方程（13）不难发现其将做无阻尼的自由振动，故而压电岛-桥结构的总能量应该守恒.本文将分别采用四阶Magnus方法和四阶Runge-Kutta方法计算岛-桥结构Hamilton函数.压电岛-桥结构的材料参数和几何参数在表1中给出.

图3分别采用4阶Runge-Kutta方法和4阶Magnus几何积分方法计算了压电岛-桥结构Hamilton函数的相对误差图，其初始条件为x1=0，x2=0.1，x3=0，x4=0 ，步长取0.5.由图3 结果不难发现：采用4阶Magnus几何积分方法得到的Hamilton函数相对误差一直在零附近震荡；而利用4阶Runge-Kutta方法得到Hamilton函数相对误差随着积分时间的增加而不断增长.对于保守系统（21），其能量应该守恒，图3的结果验证了几何积分方法保能量的优越性.

为了进一步验证几何积分方法的有效性，图4给出了岛-桥结构的时间历程曲线.由图4数值结果可以发现：利用几何积分方法得到的位移响应幅值x1能够长时间保持解的稳定性，可以认为该方法在较大积分范围内不会产生算法阻尼和数值耗散[31]；然而，经典的四阶Runge-Kutta方法自身存在算法阻尼，在迭代过程中，所得位移响应幅值x1经过数值耗散不断减小.图3和图4显示了Magnus几何积分方法在保守系统非线性数值计算方面的优越性.通过该方法得到的Hamilton函数相对误差一直在零附近震荡，而通过Runge-Kutta方法得到Hamilton函数相对误差随着积分时间的增加而不断增长，在算法阻尼的作用下，误差持续积累，最终必然会超过数值计算的误差限.

图3 Hamilton函数相对误差Fig.3 The relative error of Hamilton's function

图4 位移时间历程图Fig.4 Displacement time history diagram of the system

对于保守系统（21）的另一个重要性质是：在时间演化过程中，轨线在相空间中围成的体积不变.为了验证几何积分方法的保结构特性，分别采用四阶几何积分方法和经典的四阶Runge-Kutta方法给出了系统（21）的相图，如图5所示.其中，时间步长分别取τ=0.1s和τ=0.5s.

观察图5，从中可以发现：当步长增加时，采用几何积分方法得到的系统相空间面积保持不变，而采用Rung-Kutta方法得到的相空间会因为步长的增加，导致相空间面积增加.

由图3-图5可以说明几何积分方法能够保持保守系统的能量和结构.因此，在下一节的动力学分析中，考虑采用几何积分方法对方程（21）进行求解.

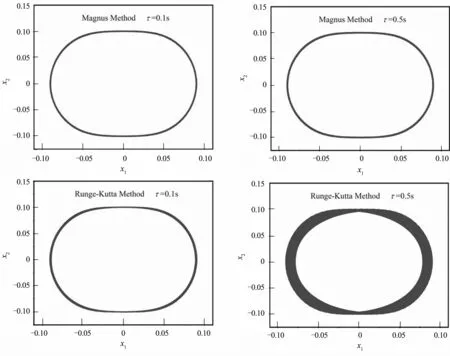
图5 不同时间步长下的相图Fig.5 Phase diagram at different time steps

4.2 岛-桥结构动力学响应

对于岛-桥结构，由振动理论可知，其无量纲固有频率为

取压电薄膜的材料为PTZ-5H，仍取表1中的材料参数和几何参数.取初值x1=0，x2=0.1，x3=0，x4=0.

表1 材料参数和几何参数[33]Table 1 Material parameters and geometric parameters[33]

为了讨论温度场和电压对压电岛-桥结构动态力学行为的影响，图6和图7给出了其对应的频谱曲线.通过数值仿真，图6和图7给出了基于压电薄膜的岛-桥结构互联导线自由振动时固有频率与温度场和膜间工作电压之间的变化曲线.

图6的数值结果讨论了温度变化量对屈曲压电结构固有频率的影响规律.从图6可以发现：当取定电压，随着温度变化量的增加，屈曲压电结构的固有频率随之增加，同时还发现其增长趋势呈线性增加趋势.对于这一现象，可以由方程（11c）进行解释：原因在于压电参数和温度参数控制的膜力N呈现线性关系.

图6 温度对压电薄膜固有频率的影响Fig.6 Effect of temperature on natural frequency of piezoelectric films

图7讨论了电压改变量对屈曲压电结构固有频率的影响规律.由图7的数值结果可以发现：随着电压的增加，系统固有频率呈线性增加，这一点仍然可以由式（11c）来解释.

图7 电压对压电薄膜固有频率的影响Fig.7 Effect of voltage on natural frequency of piezoelectric films

由图6和图7的结果，从中可以得到这样的结论：随着温度变化量和电压的增加，屈曲压电岛-桥结构的固有频率会随之增加，即说明了温度变化量和电压会使结构变“硬”.如果让岛-桥结构工作于过高的温度场和电场中，会导致该类型电子器件失稳的风险增加.

图8和图9给出了温度变化量和电压对屈曲压电岛-桥结构振动特性的影响.由图8结果可以发现：当工作电压均匀增加时，岛-桥结构振幅的峰值呈现递增趋势，而振动周期几乎没有变化，说明岛-桥结构电压对结构振动呈现正激励作用.观察图8（b），可以进一步发现：当工作电压固定时，随着温度改变量的增加，岛-桥结构的振幅会随之增加；当系统温度变化量较少时，岛-桥结构的振动幅值呈现“波动”式变化，原因在于温度场对该岛-桥结构的影响被等效成了轴向力.由方程（11）可以知道：温度变化量较小时，轴向力对原系统的影响较小，系统将会按其原固有频率振动.

图8 电压对压电薄膜振幅的影响Fig.8 The effect of voltage on the amplitude of piezoelectric film

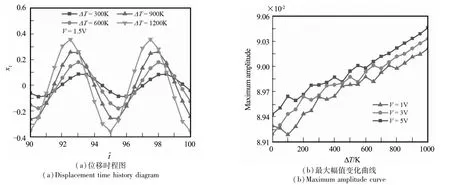
图9 温度对压电薄膜振幅的影响Fig.9 The effect of temperature on the amplitude of piezoelectric film

从图9（a）可以发现：随着温度变化量的增加，屈曲岛-桥结构振幅会随之增加；同时，岛-桥结构振动周期也发生了变化，其规律为：当温度变化量增加300K，结构振动周期将减小大约1/8，这进一步验证了图8（b）中所展示的现象—温度场能够改变岛-桥结构振动频率.由图9（b）的数值结果可以发现：当固定温度变化量时，岛-桥结构振幅会随着工作电压的升高而增加.通过对比图8（b）和图9（b），可以得到这样的规律：相比于工作电压，温度变化量对岛-桥结构振动特性的影响更大；另外，屈曲压电岛-桥结构工作于较低温度场中时，其振动呈现低幅波动振荡，而对于较高温度场作用时，结构的振动明显快速增加.因此，对于通过调整“硬”薄膜结构的振幅来实现延展性的岛-桥式柔性电子器件来说，可以通过改变工作温度和电压来提高该类电子器件的延展率及稳定性.

5 结论

针对屈曲压电岛-桥结构，本文将其等效成两端固支的梁结构.鉴于岛-桥结构的柔性电子器件会发生大变形，本文基于Timoshenko梁理论，建立屈曲压电岛 桥结构的动力学控制方程；采用Galerkin方法对原方程进行近似求解，再通过引入状态变量，将四阶常微分方程降阶为一阶常微分方程组，然后采用几何积分方法进行求解，通过数值实验，讨论了温度变化量和工作电压对屈曲岛-桥结构振动特性的影响，得到如下结论：

（1）对于保守系统，几何积分方法展现出优异的保结构，保能量特性；

（2）通过改变温度变化量和工作电压，能够改变岛-桥结构的刚度，同时，随着温度变化量和电压的增加，屈曲结构固有频率随之增加，即温度和工作电压的升高会使岛-桥结构变“硬”；

（3）在相同工作电压下，随着温度变化量的增加，屈曲结构振幅随之增加，当取定工作温度，岛桥结构的振幅也会随电压的升高而增加.另外，相比于工作电压，屈曲压电岛-桥结构更容易受温度场的影响.

本文所得结论将会为基于压电岛-桥结构的柔性电子器件设计提供理论支撑，同时，通过改变温度场和电场，能够在一定程度上改变基于压电岛桥结构的柔性电子器件的延展性和稳定性.