一类分段非线性轧机辊系系统的奇异非混沌动力学研究*
2022-08-25曾青乐源李高磊
曾青 乐源 李高磊
(西南交通大学力学与航空航天学院应用力学与结构安全四川省重点实验室,成都 610031)
引言
非光滑系统广泛存在于工程领域,近年来,由于非光滑动力系统的重要性,吸引了众多科学工作者的关注和研究[1,2],如轧机辊系系统.轧机是实现金属轧制过程的设备,一般指完成轧制材料生产全过程的设备.由放卷机、辊压系统、驱动系统、液压系统、控制系统、拆辊装置等组成.由于要适应新的产品质量要求和提高经济效益,各种特殊结构的轧机正在快速发展中.但是在钢材板带的实际生产过程中,经常会伴随各种振动的产生,其中最主要的是轧机垂直振动,垂直振动不仅会使板带精度变差,还会严重损坏机械设备,甚至制约金属轧制工艺的进一步发展.轧机辊系的振动问题一直是影响钢铁企业生产的技术难题[3].对轧机振动进行测试分析和理论分析,揭示轧机的动态运行特性,提出有效的抑振措施已成为钢铁行业的关键问题[4],因此,对此系统进行优化设计将会对实际应用带来重要意义.
奇异非混沌吸引子(SNAs)是介于拟周期运动和混沌运动之间的一种特殊的吸引子,在动力学中,这些吸引子被认为是介于规则性与混沌性之间的过渡,“奇异”指的是在相平面上动力学变量的关系并不是光滑的,而是由分形组成的,即具有几何结构上的分形;“非混沌”则是指其最大李雅普诺夫指数为负,对初值没有敏感依赖性,这也是SNAs异于混沌吸引子之处;但在相图上显示的几何性质又不同于拟周期吸引子或极限环.大量研究表明SNAs不是在一些特殊参数值上存在的退化现象,而是在拟周期激励系统中普遍存在的一种独立于混沌与周期之外的新型运动状态[5].
国内外学者对轧机辊系系统的动力学特性进行了大量的研究.孙恒[6]对六辊冷轧机垂直系统振动特性进行了分析,建立了垂直振动力学模型和数学模型,利用MATLAB计算出了系统的固有频率和主振型,获得了振型曲线,并通过仿真分析得到了上、下辊系在轧制力作用下的动态响应;马志强[7]针对轧机垂振和垂扭系统进行了特性分析和抑制振动的研究;Rigatos等[8]针对热钢轧机系统,提出了一种非线性最优控制方法.自1984年Grebogi[9]首次提出SNAs以来,奇异非混沌动力学一直是研究的热点之一,奇异非混沌的动力学现象为非混沌的复杂动力学提供了丰富的案例.Megavarna等[10]通过数值和实验方法在拟周期受迫状态控制细胞神经网络下的MLC电路中发现了通向奇异非混沌吸引子的两种路径,即Heagy-Hammel路径和分形路径,并且利用李雅普诺夫指数谱和奇异连续谱等方法进行了验证.Murali等[11]在两个正弦驱动的LCR耗散振荡器共享一个共同的分段非线性模型中,发现了SNAs的存在.通过相空间分析、庞加莱截面、李雅普诺夫指数等数值方法对所检测到的奇异非混沌现象进行了分析,并用递归量化方法对吸引子的奇异非混沌性质进行了验证.对于轧机辊系系统的奇异非混沌动力学现象,目前国内外学者尚无研究.
本文主要研究一类非线性轧机辊系系统在垂直振动情况下的奇异非混沌动力学;建立了一类轧机辊系系统垂直振动的运动微分方程,引入三维Poincaré映射;发现三类通向SNAs的途径;并运用有理数逼近以及相敏感函数验证其奇异性质.
1 动力学模型
轧机结构示意图如图1所示;从实际系统中简化出的轧机辊系动力学模型如图2所示:
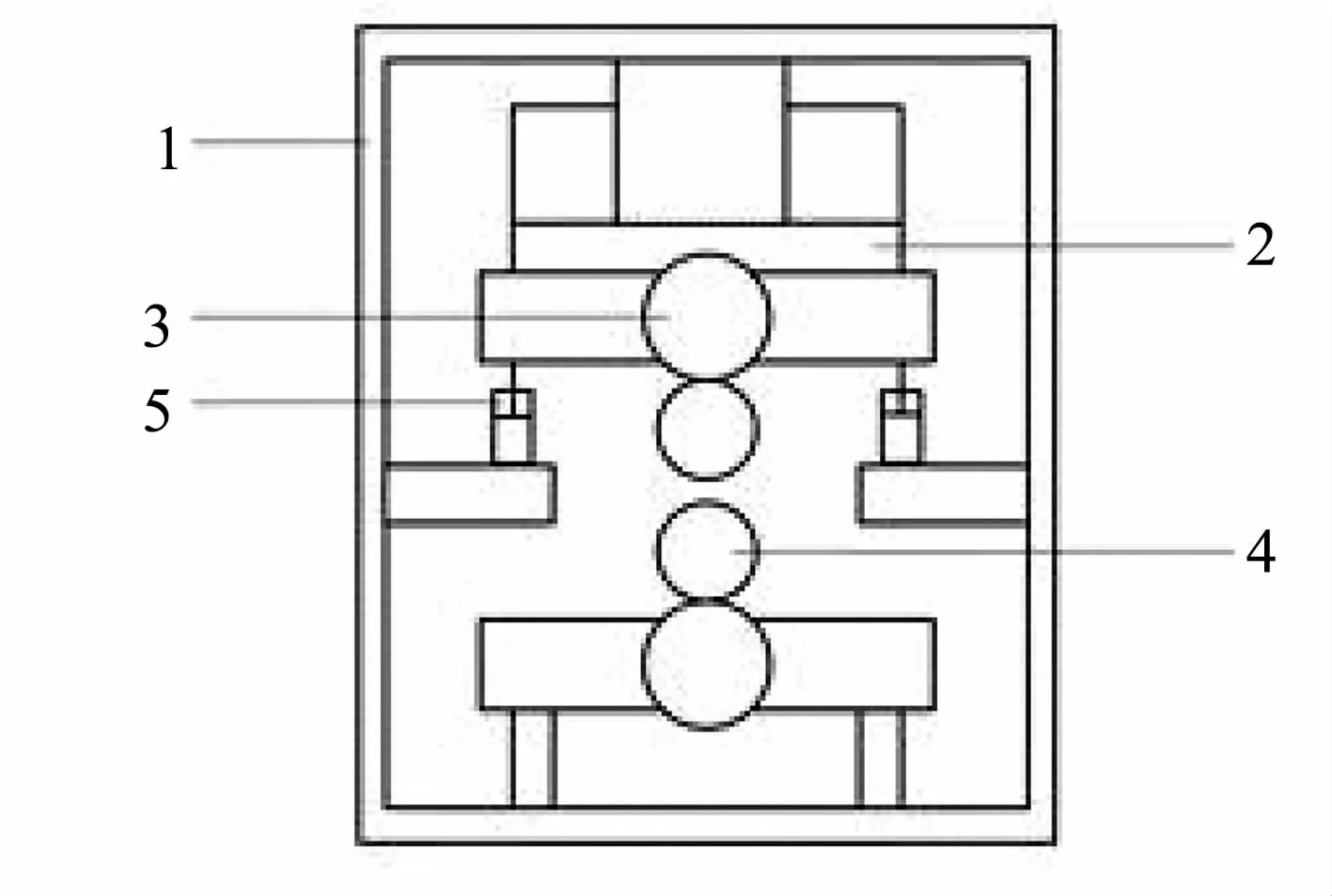
图1 轧机结构示意图Fig.1 Mill structure diagram
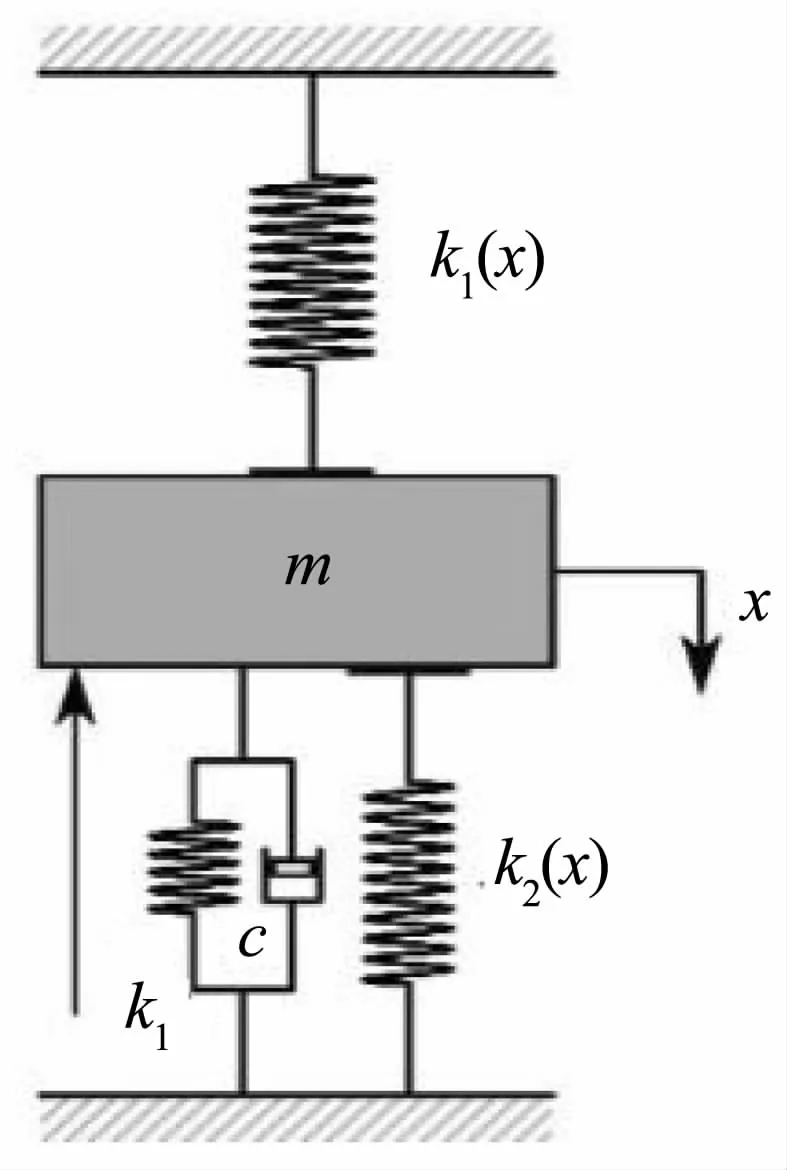
图2 轧机辊系系统动力学模型Fig.2 Dynamic model of rolling mill system
其中,m等效为上工作辊和上支承辊以及轴承座的质量;x为辊系的位移;k1和c分别为轧辊与轧件间的等效线性弹性系数和阻尼系数;K1是压下缸与辊系间的非线性弹性力;K2是平衡缸与辊系间的非线性弹性力.可表示为如下形式[12]:



2 数值模拟
2.1 吸引子的演变过程
固定参数: a1=10,a2=1,a3=1,a4=1,ξ=0.009,f=0.5,ω=1,ω0=2 时,e为控制参数,研究系统在 (θn,xn) 平面和 (xn,vn) 平面上的动力学现象.当 e=0.15 时,在 (θn,xn) 平面上存在一条不变曲线,在(xn,vn)平面上有一条不变圈,则此时系统为1个环面(1T)的拟周期吸引子,如图3所示.当控制参数e增加到0.34时,系统发生环面倍化变为2T,此时系统为2T的拟周期吸引子,如图4所示.将控制参数继续增加,当e=0.354时,出现SNAs,如图5所示;其最大李雅普诺夫指数小于零( λmax=-3.0 ×10-3),如图7(a)所示.当控制参数e继续增大到0.37时,系统将变为混沌状态,如图6所示.此时其最大李雅普诺夫指数为正(λmax=4.2 ×10-3),如图7(b)所示.

图3 1T环面,e=0.15Fig.3 1T torus,e=0.15
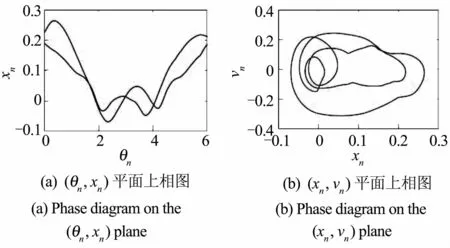
图4 2T环面,e=0.34Fig.4 2T tori,e=0.34

图5 SNAs, e=0.354Fig.5 SNAs,e=0.354
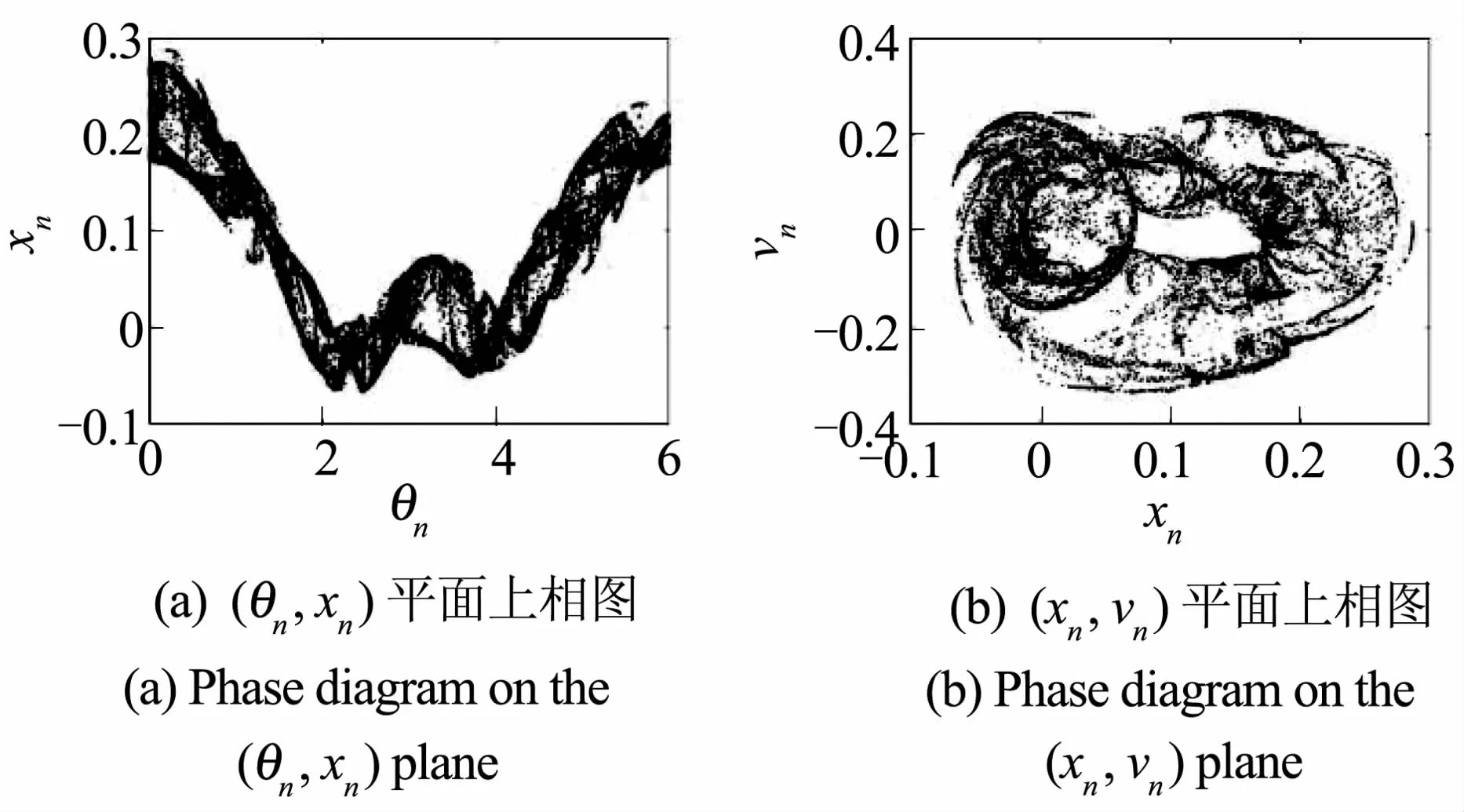
图6 e=0.37,混沌吸引子Fig.6 e=0.37,chaotic attractors
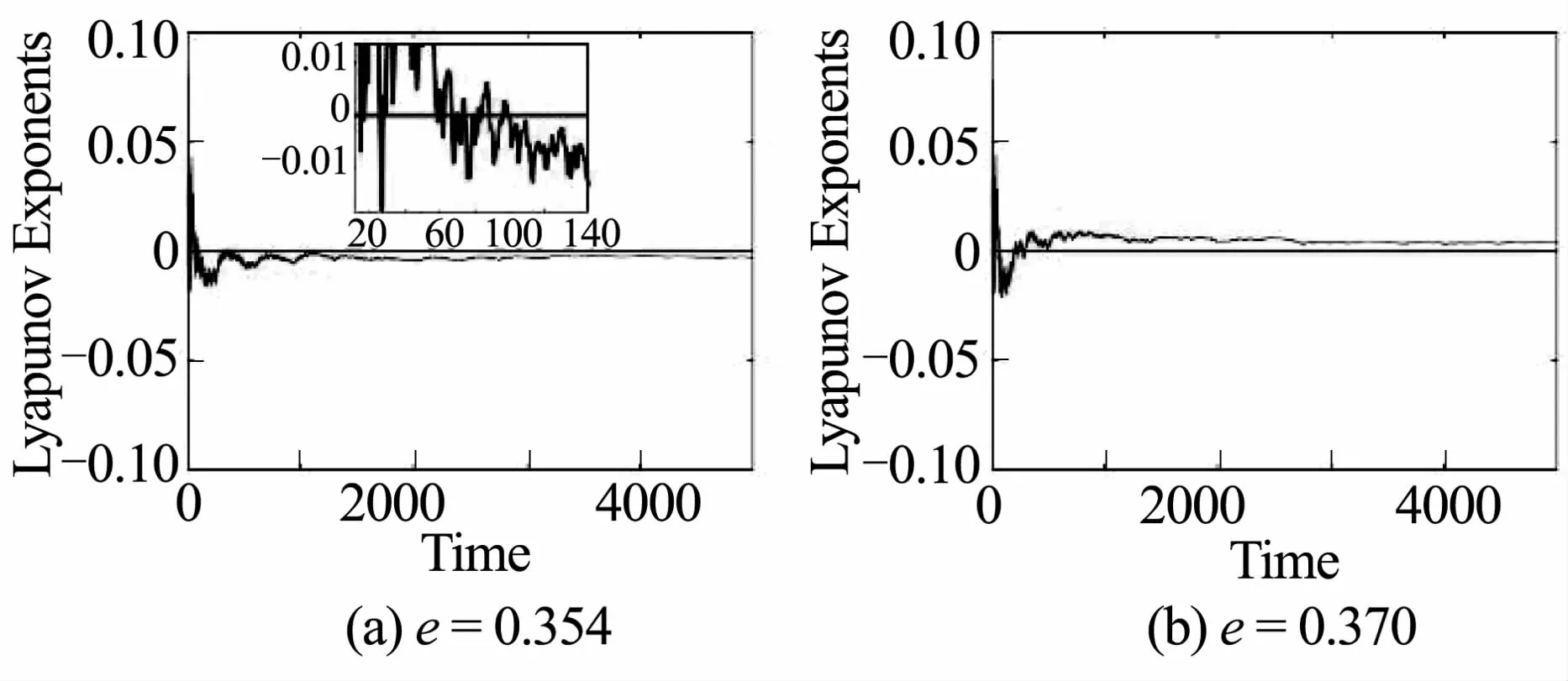
图7 最大李雅普诺夫指数图Fig.7 The largest lyapunov exponent
2.2 SNAs产生机制
2.2.1 分形路径
分形路径是指当改变系统参数时,周期环面逐渐产生褶皱,然后吸引子随参数的变化越来越不光滑,最后演变为SNAs[13].分形过程中,没有明显的不稳定集.当a1=10,a2=1,a3=1,a4=1,e=0.405,f=0.5,ω=1,ω0=2时,ξ为控制参数.当ξ=0.025时,系统为1T的拟周期吸引子,如图8所示;当ξ继续减小到ξ=0.0088时,光滑的吸引子发生变化,出现局部失稳现象,在 (θn,xn)和(xn,vn)平面上的相图均显示出明显的褶皱状态,如图9所示;当ξ减小到ξ=0.0082时,系统彻底失去光滑性,此参数下的SNAs是通过分形路径产生的,如图10所示.

图8 1T环面,ξ=0.025Fig.8 1T torus, ξ=0.025
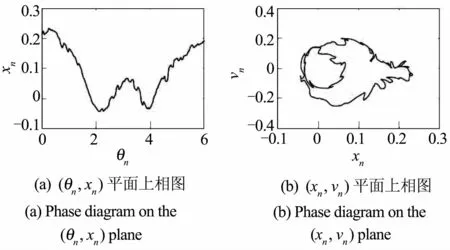
图9 1T环面,ξ=0.0088Fig.9 1T torus, ξ=0.0088

图10 SNAs,ξ=0.0082Fig.10 SNAs, ξ=0.0082
2.2.2 阵发路径
阵发-I型路径是由鞍结分岔产生的过渡到SNAs的一种路径[14].固定参数:a1=50,a2=15,a3=4,a4=10,ξ=0.0099,f=1,ω=1,ω0=2,e为控制参数.当e=0.405时,系统为1T的拟周期吸引子,如图11所示;当控制参数e增加到0.42时,系统为阵发 -I型 SNAs,如图12所示.这种路径的特点是相轨线附近有很多杂乱无序的散点聚集在其周围,但却并未出现褶皱状.
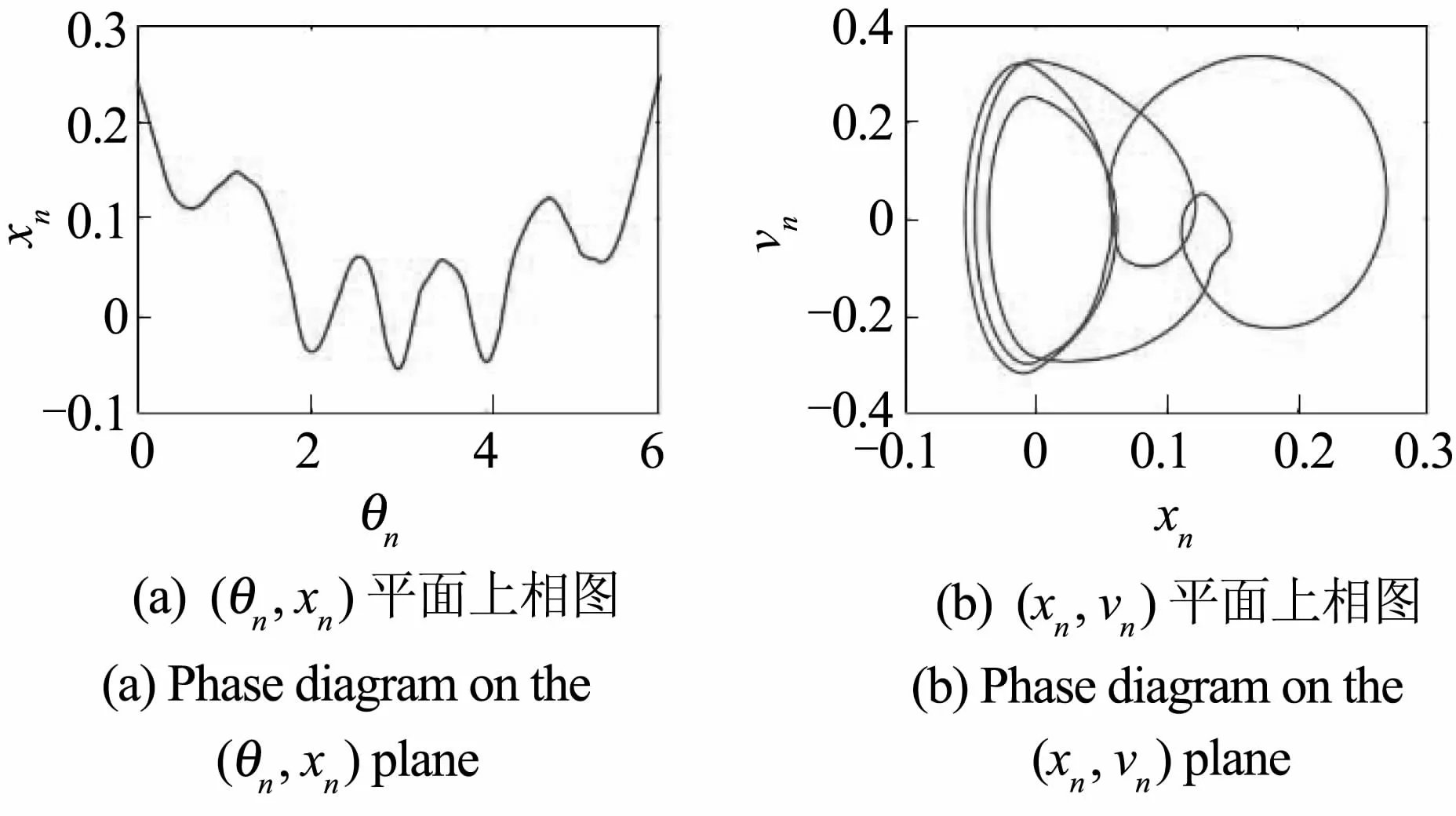
图11 1T环面,e=0.405Fig.11 1T torus,e=0.405

图12 SNAs,e=0.42Fig.12 SNAs,e=0.42
2.2.3 Heagy-Hammel路径
通常H-H路径是指一个周期加倍的拟周期环面(周期为2n环面)与它自己不稳定的母环(周期为2n-1环面)碰撞而产生的SNAs.碰撞将导致周期2n环面产生褶皱,继而产生2n+1环面.当控制参数继续增加时,此2n+1环面将与其母环2n环面碰撞.在这个过程中继续起褶,产生2n+2环面,以此类推.通过 Heagy-Hammel路径演变为SNAs已经在几类拟周期受迫非线性动力学系统中研究过[15,16].当 a1=10,a2=1,a3=1,a4=1,ξ=0.009,f=0.5,ω=1,ω0=2时,当e=0.352时,系统为2T的拟周期环面,如图13所示;当e继续增加到0.354时,2T的拟周期吸引子发生碰撞,演变为SNAs,如图14所示.
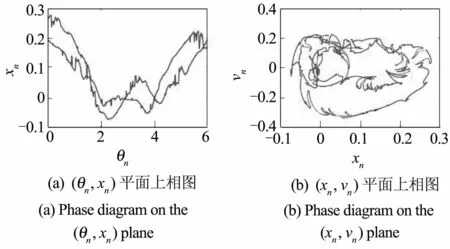
图13 2T环面,e=0.352Fig.13 2T tori,e=0.352
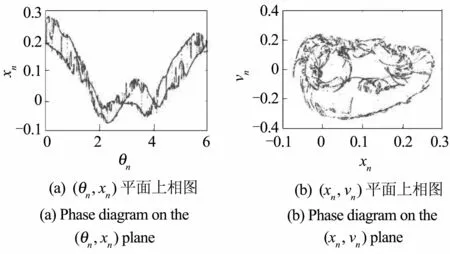
图14 SNAs,e=0.354Fig.14 SNAs,e=0.354
3 奇异性验证方法
3.1 有理数逼近
每一个无理数都可由有理数去逼近到任何想要的精度,即有理数在实数中是稠密的[17].当系统的某个参数变化时,有理数逼近无理数在研究向SNAs演变的过程中是非常有用的方法[18].利用无理数的连分式表示可得到其有理近似.使用连分数,可以表示出所有实数.对于有理数来说,可表示为有限连分数,对于无理数来说,可无限逼近.对于黄金比例值ϕ=(-1)/2的连分数可以用斐波那契数列逼近[19],具体表达式为:ϕk=Fk-1/Fk,其中, Fk=0 ,1,1,2,3,5,8,13,21,…通过有理数逼近无理数验证其奇异性,取ϕk分别为89/144,377/610,610/987,28657/46368,如图 15 所示.当ϕ13=89/144时,可以观测到在(xn,vn)平面上吸引子有稳定且可数的周期点,当k继续增加时,在(xn,vn)平面上的周期点数明显增加;ϕ25=28657/46368时,与SNAs近乎一致.当阶数k趋近于无穷时,相平面上的点也趋于无穷,且逼近的吸引集是非光滑的,不具有分段可微性,即为SNAs[20].结果表明,阶数越高,吸引子的几何特性越接近SNAs.

图15 (xn,vn)平面上有理数逼近SNAsFig.15 Rational approximation of the SNA in the(xn,vn) plane
3.2 相敏感函数
采用吸引子对相位的导数可验证奇异性质.这种方法是基于吸引子对外力相位具有敏感性[21].

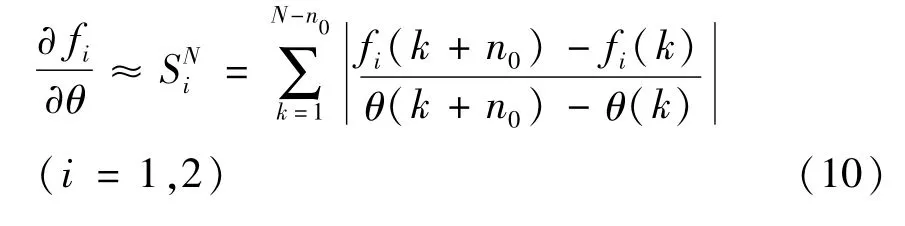
其中,k+n0≤N,fi(k)是对fi的第k次迭代.令N次迭代后的最大值为,有:

当N→∞时,几何性质表现为若γNi无穷大,则SN→∞,则说明吸引子非光滑,具有奇异性;若有界,则不具有奇异性.图16为系统分别在控制参数e=0.42和e=0.405的相敏感函数;当e=0.42时,趋于无穷大,此时系统为SNAs,当e=0.405时,不具有奇异性.

图16 相敏感函数图Fig.16 Diagram of phase sensitivity function
4 结论
本文研究了一类拟周期激励的单自由度分段非线性轧机辊系系统,发现在这类非光滑系统中存在多种路径可以产生奇异非混沌吸引子;即分形路径、阵发路径以及Heagy-Hammel路径.奇异非混沌的性质通过相图、李雅普诺夫指数、有理数逼近和相敏感函数进行验证.本文的结论可为非光滑动力学系统中的混沌控制提供理论依据,避免此系统长期工作在混沌状态,以致板带精度降低,产生巨大噪声,甚至损坏设备.
