基于ADRC的PMSM无传感器控制及参数辨识

赵凯岐，刘 洋

(哈尔滨工程大学智能科学与工程学院，哈尔滨 150000)

0 引言

永磁同步电机(permanent magnet synchronous motor,PMSM)具有损耗小、功率密度大、起动转矩大、效率高等优点，已经广泛地应用在航空航天、船舶电力推进等诸多领域，成为电力传动领域的研究热点[1-4]。在传统永磁同步电机控制策略中，矢量控制(field oriented control,FOC)是应用较为广泛的控制方式，FOC通过坐标变换将定子电流完全解耦为励磁电流和转矩电流分别控制，拥有较高的控制精度，但是需要较为精确的转子位置角，传统方法是通过机械位置传感器确定转子初始位置，这不仅增加了电机成本，还降低了电机的可靠性和稳定性[5-7]。因此PMSM的无传感器矢量控制技术应运而生[8]，如滑模观测器、自适应观测器、扩展卡尔曼滤波器、龙贝格观测器等。在电机运行过程中，不可避免存在参数的实时变化、外界不确定的干扰等问题，PI控制器对线性系统具有结构简单，稳定性好等优点，但是PMSM是非线性系统，当调速范围要求很宽时，PI控制器很难在不同负载情况下保持良好的控制精度。

彭思齐等[9]设计了自适应模糊观测器的PMSM矢量控制，虽然自适应观测器保证了转子位置的精度，解决了传统滑模观测器的抖振问题，但是整个系统还是基于PI控制，不能保证在电机运行过程中，参数变化时的控制性能，进而会引起转速超调等问题。现如今对PI控制器优化的方法有很多，如将算法与PI控制器结合并对PI参数在线整定，或者利用滑模控制器取代PI控制器。刘宗锋等[10]采用PI和内模控制相结合的方法，实现了PI参数的在线整定，提高了系统的调速性能，在一定程度上提高了控制系统的鲁棒性。王飚等[11]采用二阶滑模观测器的内嵌式永磁同步电机改进PI控制，取消了传统滑模观测器的低通滤波器和位置补偿环节，抑制了抖振及相位延迟问题，改善了系统动态性能；唐文秀等[12]采用优化扩展卡尔曼滤波器的电机参数估算方法，保证控制器电机模型电感和磁链同步跟随实际的电机电感和磁链，达到消除电流静差的目的；孙斌等[13]采用自抗扰控制代替传统的PI控制，能够提高系统的抗扰能力，抑制了转速超调，提高了系统的鲁棒性。通过对PI控制器进行优化创新或替代，在一定程度上系统抗干扰能力会提高许多，但是转子位置和转速的精度没有得到保障，在增强抗干扰能力的同时能够保证观测精度是如今的研究热点。

针对PI控制的缺陷，韩京清[14]提出了自抗扰控制(active disturbance rejection control,ADRC)。虽然ADRC相较于传统控制系统具有更好的控制性能，但是电机在实际运行过程中，随着转速的变化以及负载的改变，相应参数是时刻改变的，这使得转子位置和转速出现误差，给系统补偿干扰带来困难。扩展卡尔曼滤波器(extended Kalman filter,EKF)是一种递推算法，通过反复迭代抑制环境的未知白噪声，针对非线性系统具有良好的观测性能，能够精确观测电机参数。文中提出EKF结合ADRC引入FOC系统中，具体分析了实现方法。将ADRC替代传统PI速度调节器，利用EKF对转速和转子位置精确估计，在满足系统非线性的同时，还保证了参数估计的精度。仿真结果表明：该策略保持了FOC良好的稳定性以及EKF有效地抑制噪声能力，增大了系统的抗干扰能力，提高了系统鲁棒性，实现了PMSM的无传感器矢量控制。

1 PMSM 数学模型

FOC的基本思想是建立在旋转坐标系下，因此在d、q同步旋转坐标系下，PMSM数学模型表示为：

(1)

PMSM转矩方程表示为：

Te=Pψfiq

(2)

PMSM机械运动方程表示为：

(3)

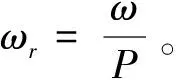
由于在α、β静止坐标系下定子电压和电流的测量值不需要通过复杂的坐标变换转换到旋转坐标系，降低了PMSM数学模型的非线性，使系统采样周期变短，系统计算时间也会减少，估算精度将得到提高，因此在α、β静止坐标系下，PMSM数学模型表示为：

(4)

式中，uα、uβ为定子电压α、β轴的分量；iα、iβ为定子电流对应α、β轴的分量；ψα、ψβ为定子磁链对应α、β轴的分量；θ为转子位置角。

2 扩展卡尔曼滤波器算法分析

2.1 EKF原理

具有随机干扰的线性离散过程的状态方程和观测方程为：

(5)

式中，xk是系统状态变量；wk为系统的随机噪声；vk为测量噪声，其协方差矩阵分别为R、Q。由于系统运行过程中，系统噪声和测量噪声时刻变化，为了方便计算，将协方差矩阵R、Q取为常数。wk和vk为未知白噪声，有p(w)～N(0,Q)，p(v)～N(0,R)成立。

预测阶段：

(6)

(7)

更新阶段：

(8)

(9)

(10)

2.2 EKF观测器设计

由式(4)电流方程，构建状态方程和输出方程，选取α、β静止坐标系下电流分量、电机转速和转子位置作为状态变量，定子电压作为输入控制量。对于EKF，状态变量一般为不可直接测量的量，而输出量为方便直接检测的量。结合PMSM特性选择如下：

x=[iαiβωθ]T

u=[uαuβ]T

则系统的非线性方程：

(11)

式中，

由于i可直接观测到，定义测量方程为：

y=h(x)+v

(12)

由上式可知PMSM为一个四阶非线性系统，一些不可直接测量的量被选作状态量时就可以借助EKF状态观测的功能得到。因此选取电流分量、电机转速和位置作为状态变量，电压作为输入。

要实现非线性系统线性化，对f(x),h(x)进行矩阵求导处理，乘以采样周期Ts离散化后得到：

扩展EKF算法因为可靠性和精度都较高，能够同时对转子位置和转速进行估计，符合FOC对参数精度的要求，在电气传动领域得到了广泛采用。

2.3 协方差矩阵参数选取策略

关于上述方程式(6)～式(10)的几个参数：Q、R、p0一般取为对角阵即可，因为相对于对角元素，非对角元素影响很小，忽略不计。EKF的核心是通过测量值与预测值的偏差对预测状态进行反馈校正，进而得到最优值，因此合理设计EKF增益矩阵是技术关键。对系统是否收敛以及稳态的观测精度影响较大的是Q、R的选取。系统噪声协方差矩阵Q反映系统噪声的影响，它代表着控制对象本身对干扰噪声的抑制能力。增大Q由式(7)和式(8)可知，便是增大系统的扰动，滤波器增益Kk变大，则修正量变大，使系统动态性变快，但是Q不可能无限增大，因为这样意味着系统不可靠。通常设置为q11=q22，调整参数时q11与q22越小，或q33越大，则估计滞后越小，系统响应越快，但是取值不当容易导致系统发散，q44对系统几乎没有影响。测量噪声协方差矩阵R，代表观测器或电流电压检测装置引入的测量误差大小，增大R表示抑制噪声干扰能力差，滤波器增益Kk会变小，与Q的调节矛盾，导致观测系统滞后严重，动态性能变差，因此通常先调节Q获得理想的动态响应速度，再调节R改善稳态性能。通常R取为2×2对角阵，为方便调试r11=r22影响不大。而估计协方差矩阵初始值p0对动态响应和稳态精度影响很小，其中p33不同会导致位置估计θ起点不同，但不影响形状。实际系统运行过程中，系统噪声和测量噪声时刻变化不可能得到精确的信息，因此协方差矩阵Q、R选择是调试过程的难点，通常根据随机特性确定。本实验中扩展EKF观测器的几个参数设置如下：

3 基于ADRC控制器设计

3.1 ADRC原理及参数分析

ADRC是由非线性跟踪微分器(TD)、扩张观测器(ESO)、非线性状态误差反馈(NLSEF)组成的[15]。TD作用是为给定信号设置过渡过程并且提取信号的微分值；ESO能实时估计出控制系统所受扰动并加以补偿；NLSEF将TD与ESO进行组合，利用非线性函数将状态误差变为初始控制量。一阶被控系统的ADRC方程可以表示为：

一阶系统非线性跟踪微分器：

(13)

式中，fal(e0,r,T)可以定义为：

式中，v1为ADRC的给定信号；v*为v1的跟踪信号；r为速度因子；T为采样周期；fal(e0,r,T)为最优综合控制函数；sgn为符号函数。

由上式可知TD中只有参数速度因子r需要整定。通过调整r的大小可以改变估计转速对转速给定值的跟踪速度，为确定其调节方向，给出不同r下的转速仿真波形。

由图1可知，随着r的增大，过渡过程达到给定转速100 r/min所需要的时间越短，但是r不可以无限增大，否则会导致转速波形超调甚至发散，本系统r取1000。

一阶系统扩张观测器：

(14)

式中，α1、α2为非线性因子；β1、β2为误差增益；δ1为滤波因子；b0为补偿因子；z1为y的跟踪信号；z2为扰动估计值。

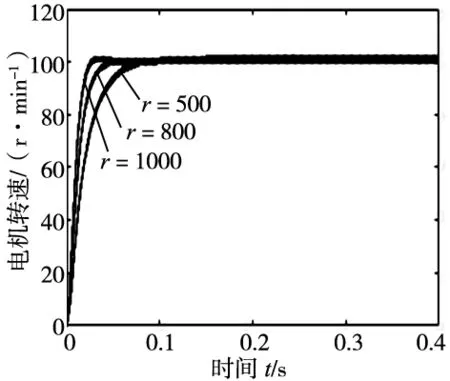
图1 不同r的电机空载转速波形

ESO中需要整定的参数有α1、α2、β1、β2以及δ1，非线性因子α1、α2为经验参数，取值范围一般为0.9～1，本系统中均取0.9；滤波因子δ1也为经验参数，取值范围一般小于0.01，本系统取0.001。误差增益β1、β2参数取值方向需要根据仿真波形具体分析，其空载转速波形如图2、图3所示。

图2 不同β1的电机空载转速波形 图3 不同β2的电机空载转速波形

由上图可知，β1、β2对转速均有相似的影响，当β1取值过大时，转速曲线左移并且出现超调，反之转速曲线右移，但是也会出现超调。当β2取值过大时，转速会出现超调，反之峰值则达不到给定转速，但并不会影响曲线的上升速度。因此在整定误差增益时，应该按照从小到大的方向整定，当转速波形出现明显超调时，再略微减小，直至取到最优值，本系统β1取值7000，β2取值100 000。

非线性状态误差反馈：

(15)

式中，β3为误差增益；δ2为滤波因子。

fal函数的表达式为：

(16)

NLSEF中需要调节的参数有δ2和β3，其中滤波因子为经验参数，本系统取0.001；β3与β1、β2的调节方式相同这里就不再赘述，本系统β3取值25 000。

3.2 基于ADRC的速度调节器设计

由PMSM的运动方程得：

(17)

从上式可以看出，转速ω受到TL、iq的影响，进而影响系统的控制精度，根据ADRC原理将以上参数视为速度环的扰动，记作w(t)。进而由ADRC观测并加以补偿，因此上式可以整理为：

(18)

式中，

设计一阶TD模型，如下：

v1=-rf(v1-ω*,r,T)

(19)

设计ESO模型，如下：

(20)

ADRC速度调节器结构图如图4所示。

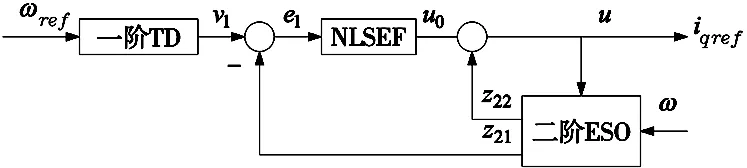
图4 基于ADRC的速度调节器结构图

4 基于EKF的PMSM矢量控制MATLAB仿真及结果分析

为验证方案的可行性，根据图5所示的系统控制框图，在MATLAB软件中的Simulink功能模块搭建系统仿真模型，对PMSM基于传统PI，基于PI-EKF，基于ADRC-EKF分别进行仿真。本模型采用固定步长2e-6，ode23tb算法。采样时周期为2 μs，仿真时间为0.4 s，进行空载和负载试验。首先给出仿真过程中PMSM模型参数设定情况，如表1所示。

图5 基于ADRC-EKF的三相PMSM无传感器矢量控制图

表1 电机仿真模型参数

给定转速为100 r/min，运行到0.1 s时转速上升为200 r/min，在0.2 s时加入1.5 N·m负载，图6、图7分别为采用基于传统PI、基于PI-EKF和基于ADRC-EKF的FOC控制转速波形。

图6 3种控制方法的电机低速波形

图7 3种控制方法的电机低速波形局部放大图

前0.1 s给定转速为100 r/min时，在基于传统PI的系统中，转速波形的超调在0.025 s时达到了120 r/min，在0.08 s系统才达到稳定的100 r/min；在基于PI-EKF的系统中，转速波形的超调已经得到明显改善，曲线平滑，但转速上升阶段的响应速度相对于另外两种控制方法较慢；在基于ADRC-EKF系统中，电机启动阶段，转速曲线上升比较平滑，无超调，在0.025 s时达到稳定的100 r/ min。0.1 s～0.2 s给定转速加至200 r/min时，和上述情况相同，这里不再赘述。0.2 s时加入1.5 N·m负载，基于传统PI的系统中，转速重新达到200 r/min用时0.1 s；在基于PI-EKF的系统中，转速重新达到200 r/min用时0.15 s；在基于ADRC-EKF系统中，转速重新达到200 r/min用时0.08 s。具体如图8～图10所示。

图8 基于传统PI的电机低速转矩波形 图9 基于PI-EKF的电机低速转矩波形

前0.1 s给定转速为100 r/min时，在基于传统PI的系统中，转矩达到稳定值用时较长，并且转矩变化出现明显的抖振。相比较而言，另外两种控制方法可以有效改善电磁转矩的抖振现象。

给定转速为1200 r/min，在0.2 s时加入5 N·m负载，图11、图12分别为采用基于传统PI、基于PI-EKF和基于ADRC-EKF的FOC控制转速波形。

图10 基于ADRC-EKF的电机低速转矩波形 图11 3种控制方法的电机高速波形

图12 3种控制方法的电机高速波形局部放大图

前0.2 s给定转速为1200 r/min电机空载运行，在基于传统PI的系统中，转速波形的超调在0.038 s时达到了1420 r/min，在0.08 s系统才达到稳定的1200 r/min；在基于PI-EKF的系统中，转速波形的超调在0.048 s达到了1280 r/min，已经得到明显改善，曲线平滑，在0.07 s系统才达到稳定的1200 r/min，但转速上升阶段的响应速度仍较慢；在基于ADRC-EKF系统中，电机启动阶段，转速曲线上升速度较快，甚至已经超过了传统PI的响应速度，无超调，在0.029 s时转速超调达到1250 r/min，相较于另外两种控制方法，转速超调已经得到明显的优化，在0.065 s时达到稳定的1200 r/min，达到稳定的时间也得到优化。0.2 s时加入5 N·m负载，基于传统PI的系统中，0.27 s时转速出现了30 r/min的明显超调，转速重新达到1200 r/min用时0.15 s；在基于PI-EKF的系统中，转速重新达到1200 r/min用时0.1 s；在基于ADRC-EKF系统中，转速重新达到1200 r/min用时0.1 s，在加入负载时出现的转速跌落更小。

图13、图14分别为转速1200 r/min时，采用基于PI-EKF和基于ADRC-EKF的FOC控制电流波形。

图13 基于PI-EKF的电流波形 图14 基于ADRC-EKF的电流波形

空载时，在基于ADRC-EKF系统中，0.05 s前电机两相静止电流的估计值和实际值就稳定在零附近，而基于PI-EKF的系统中电流稳定在零附近所用时间均大于0.05 s。负载时，在基于ADRC-EKF系统中，电流为平滑稳定的正弦波形，而基于PI-EKF的系统中存在电流超调现象，相比之下基于ADRC-EKF系统性能更优越。

由图15、图16可知在前0.012 5 s时，转子位置的估计值跟踪实际值存在一定误差，而基于ADRC-EKF的系统转子位置估计值能很好的跟踪实际值，因为电机在刚启动时转速较低，ADRC调节器具有良好的动稳态性能和补偿性能，提高了转子位置估计在动态时候的跟踪速度和精度。随着仿真时间的增加，两种控制方式误差逐渐减小，最终转子位置估计值都更接近实际值。

图15 基于PI-EKF的转子位置波形 图16 基于ADRC-EKF的转子位置波形

5 结论

本文的研究对象是PMSM，将基于EKF观测器和ADRC速度调节器相结合，从而实现无传感器设计。以PMSM数学模型为基础，完成了基于传统PI，基于PI-EKF以及基于ADRC-EKF的系统设计。通过3种控制方式的仿真结果对比，验证了基于ADRC-EKF的控制系统在转速控制、位置辨识以及参数估算精度上都有更优越的性能，具有比传统PI调节器更强的抗干扰能力和补偿能力。将ADRC与扩展EKF相结合，进一步满足了FOC对参数精度的要求，提高了系统的可靠性，该系统在工程中满足要求宽调速范围、高精度和高抗扰能力的场所。