培养学生数学建模素养的可视化教学案例
2022-08-25江苏省无锡市堰桥高级中学华燕萍
江苏省无锡市堰桥高级中学 华燕萍 胡 燮
新课标提出了高中数学的六大核心素养,数学建模就是这六个核心素养之一。教材主要通过应用题教学来培养学生的数学建模素养,高考试题也通过应用题重点考查学生的数学建模素养。另外,现代高新科技的发展几乎离不开数学建模,数学建模是用数学方法解决实际问题的第一步,它正以空前的广度和深度向一切领域渗透,成为一项重要的“数学技术”。所以,培养学生数学建模素养至关重要,它能提升学生的数学应用能力及综合能力,顺应时代发展的要求。
数学建模并不等同于解数学应用题,解应用题是数学建模的中低等层次要求,达不到数学建模的专项要求。但考虑课时安排及高中学生现有学习能力等各种因素,日常教学中以往的教材以应用题的形式来培养学生的数学建模的基本素养。不过相较于笔者执教多年的苏教版教材,新的人教A版做出了新的尝试与突破,笔者执教人教A版新教材数学必修1以后发现其在数学建模方面主要有两点突破。1.在第四章“指数函数与对数函数”后面设置了数学建模专题(P162-166),展现真正的数学建模的全过程,解决过程中需提出假设、实验获取数据等对于学生来说都是全新的挑战,专项要求很高。2.人教A版应用题对实际问题真实性的简化程度比苏教版少。实际问题的真实性往往较复杂,甚至涉及复杂的专业知识,所以教材上的应用题基本都会对真实性进行适度简化,人教A版对实际问题真实性的简化程度较小,所以相比于苏教版,人教A版应用题情境复杂、阅读量大。而解应用题的关键就在审题,建立恰当的数学模型,将问题转化为数学问题。阅读量大对学生审题建模造成很大困难,本论文就聚焦于人教A版的大阅读量应用题,采用“可视化”教学手段,教学生快速提取应用题中的关键信息、厘清它们之间的逻辑关系,从而快速建立起数学模型,解决阅读量大对学生审题建模造成的困难问题,提升学生的学生数学建模能力和素养。
选取人教A版必修1第70页的例8为例,此应用题是个纳税问题,整个题目(不包括解答)占据A4大小纸张的四分之三版面,文字量531个(一个数据统计为1个文字,如数据189600统计为1个文字,标点符号和运算符号不计)。这么大阅读量的应用题在苏教版教材上从未出现过,是一般应用题阅读量的4倍左右。这不是读一篇通俗易懂的文章,学生需要大致了解各种专业词汇,如“个税税额”“应纳税所得额”“综合所得”等,厘清各种量之间的关系,但是看到这么长的题目、这么多专业词汇,学生已经产生恐惧心理,顿时丧失解决问题的信心。鼓励学生耐下心来,多读几遍,估计也是于事无补,所以采取有效的教学手段,帮助学生真正地突破这个难点,让学生看到是有简单易行的方法可以有效解决审题困难这个问题的,才能真正提升他们审题的信心和能力,以后碰到这么大阅读量的题目,也就不会产生畏惧心理。
具体怎样进行审题建模的可视化教学呢?分为以下两个步骤。
第一步,审题整理关键信息。教师带着学生一起读题,要求:第一,边读边画出关键信息,这可以帮助学生排除次要信息的干扰,聚焦于关键;第二,边读边标注、画图、列表等,帮助理解和厘清各种量之间的关系;第三,边读边翻译一些能够很快推出的量。(见图1)
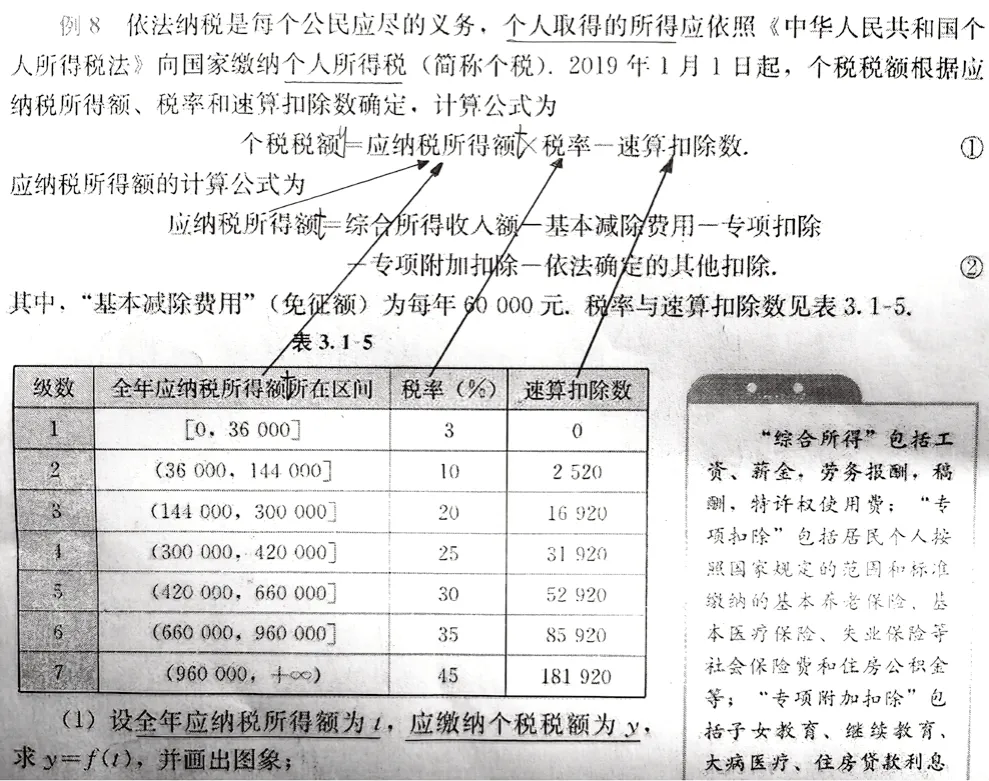
图1
第二步,建模提取相关数据,可以采用先整体后细化局部的方法,或者先局部后拼凑整体的方法,从刚才画出和标注出来的数据当中提取所需要的数据。
问题(1)建模分析:刚才审题至问题(1)时,我们立即在公式①中标注了相应的字母y和t,在表格中也标注了字母t,所以要建立这个函数模型一下子就让学生关注和意识到公式①就是此问题的函数模型y=f(x),模型的整体就建立好了,接下来要寻找和细化公式①涉及的另外两个量——税率和速算扣除数,这两个局部量根据箭头所指马上关注到表格中税率和速算扣除数,发现其有7组取值,由全年应纳税所得额t所在区间决定,于是意识到要对自变量t进行分类,建立y关于t的分段函数模型。解题过程如下:
(1)解:根据表3.1-5,可得函数 y =f(t)的解析式为

接着对第(2)问进行审题(见图2)。
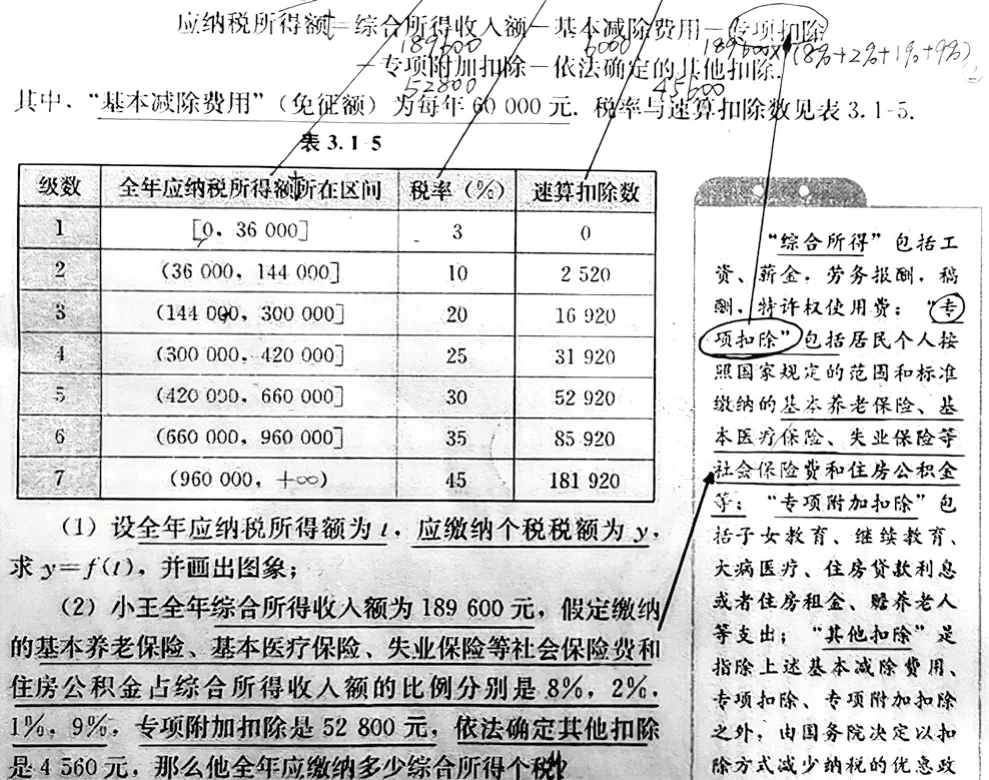
图2
画出关键信息,把相关数据标注到公式②中,发现除了条件“基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别为8%、2%、1%、9%”外,其他条件数据都能标注到公式②的相应项中,公式②还剩下“专项扣除”这一项,这时再到右侧的旁注中找“专项扣除”,就能明确第(2)问的条件“基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金”就是“专项扣除”,连用两个箭头将第(2)问、右侧旁注以及公式②中有关“专项扣除”的内容联系起来,并将数据标注到公式②的“专项扣除”下方,这时公式②中的应纳税所得额t就能翻译出来了。
对第(2)问进行建模分析,翻译目标——全年应缴纳的综合所得个税y,自然要用公式①求解,而公式①已经在第(1)问中建立起具体的函数解析式,于是目光转向第(1)问的分段函数解析式③,到底要用其中哪个表达式由t的范围决定。而刚才第一步审题时,已经边画边翻译了应纳税所得额t(见图3),计算出结果,就能知道代入③的哪个表达式了。思路清晰地可视化为:由公式②算出t→据t选择③中的相应表达式。按此两步骤操作完成如下:

图3
(2)解:根据②,小王全年应纳税所得额为
t=189600-60000-189600(8%+2%+1%+9%)-52800-4560
=0.8189600-117360
=34320.
将t的值代人③中的第一个表达式,得
y=0.0334320=1029.6.
所以,小王应缴纳的综合所得个税税额为1029.6元.
在上述可视化的审题建模方法中,第一步审题,画出关键信息排除次要信息干扰,相当于在减少阅读量,阅读量大的问题就解决了;边读边译,边读边标注、画箭头找关系等整理信息的手段帮助学生将各个量之间的关系及逻辑可视化,从而快速厘清关系理解题意。第二步建模,关注整体、细化局部就厘清了逻辑,将思路可视化,然后按图索骥提取相关数据便可。
可视化的审题建模方法关键就在于将重要信息通过恰当选取、边读边画、翻译、标注、画箭头、绘图、列表等手段,将关键信息整理分析,将关系、逻辑、思路可视化,不需要学生耐下性子多读几遍题目,通过一遍多的阅读审题就可快速建模,提升学生的数学建模信心、能力和素养。
