对人体姿态估计热图误差的再思考

杨飞宇，宋展，肖振中，莫曜阳，陈宇，潘哲，张敏，张遥，钱贝贝，汤朝伟，金武

（1.中国科学院深圳先进技术研究院，广东深圳 518055；2.奥比中光科技集团股份有限公司，广东深圳 518063；3.南京航空航天大学能源与动力学院，南京 210016）

0 引言

近年来，深度学习［1］的快速发展极大地提高了人体姿态估计算法的表现。在众多的基于深度学习的算法中，基于热图的算法取得了最佳的表现［2-6］。热图解码利用神经网络预测的热图估计人体关节点的坐标。与图像分类［7-9］、目标检测［10-12］和语义分割［13-14］等计算机视觉任务不同的是，人体姿态估计算法采用的度量指标将预测和标注的人体关节点进行点对点的比较，所以人体姿态估计任务对采用的热图解码算法的可靠性十分敏感。另外，大多数应用场景都要求进行实时的人体姿态估计，对热图解码算法的速度也提出了严格的要求。因此，开发快速、精确的热图解码算法，高效高精度地计算人体关节点的坐标具有重要意义。

现有的热图解码算法专注于消除热图的随机误差，忽略了系统误差的影响。比如，标准热图解码算法取热图上的最大响应点的坐标作为关节点的坐标，该算法简单但容易引入较大的误差。文献［15］通过将最大响应点的坐标向第二大响应点坐标移动1/4 的距离所得到的坐标作为预测的人体关节点的位置。该算法利用了热图的两个极值点，在某种程度上能减小随机误差，但效果有限。文献［16］在此基础上开展了进一步研究，通过计算热图的一阶和二阶导数来解高斯分布的平均值。这种算法利用整个热图减小随机误差，也达到了目前最佳的精度水平。但是由于需要高斯平滑前处理操作，该算法的速度较慢。从以上研究可以发现，现有的热图解码算法只处理随机误差，忽略了特定网络带来的系统误差的影响。

为了考虑系统误差的影响，本文利用神经网络在训练集上的误差表现补偿模型在推理阶段的误差。本文定义了一个最佳的误差补偿因子以描述网络的误差特性，并用于开展误差补偿。该算法可以很容易地与任意基于热图的神经网络集成，而无需更改模型设计。

本文主要工作包括：1）通过实验发现了目前基于热图的算法存在显著的系统误差，而之前的热图解码算法都忽略了系统误差的存在；2）通过理论推导给出了结合神经网络和训练集评估和补偿误差的算法。

1 相关工作

1.1 姿态估计

得益于神经网络技术的飞速发展［1］，姿态估计进入了一个快速发展的新阶段。人体姿态估计通常分为单人和多人任务。单人姿态估计只检测人体关节，无需检测关节点之间的连接关系，因此具有相对较高的精度［2-3，17-18］。多人姿态估计又分为两类：自上而下算法［4］和自下而上算法［19-21］。自上而下的算法本质上是将行人检测与单人姿态估计相结合。首先通过行人检测算法（比如YOLO（You Only Look Once）［11］和 Mask R-CNN（Mask Region-based Convolutional Neural Network）［10］等）检测出行人的外接框，然后用每一个外接框裁剪出每一个人体实例，最后用单人姿态估计网络（比如级联金字塔网络（Cascaded Pyramid Network，CPN）［4］和高分辨率网络（High-Resolution Network，HRNet）［2］等）去检测每个人体实例的骨架关节点。比如CPN［4］通过多级精细化的方法定位更精确的人体关节点位置；张小娜等［22］设计了对称空间变换网络与单人姿态估计网络相连接，实现在遮挡情况下更精确的预测；田宇［23］提出了基于沙漏网络的轻量化的自上而下的人体姿态估计网络，能够实现在复杂场景下相对快速的推理。两阶段过程通常比较耗时，需要同时使用行人检测和单人姿态估计两个神经网络，但具有较高的精度。因此，目前人体姿态估计任务精度最高的算法大多是基于自上而下框架实现的［3］。自下而上的算法在学习关节点坐标的同时，还要学习关节点之间的连接关系以达到区分不同实体的目的［19-21］。代表性的连接关系学习策略包括学习相邻关节点的连接（OpenPose）［19］，通过关联嵌入分组学习人体关节（Associative Embedding）［20］和通过概率学习连接（Pose Proposal Network）［21］。

1.2 热图解码

学术界对人体姿态的研究主要集中在设计不同的网络架构，对热图解码研究较少，然而热图解码却对最终预测的精度有显著的影响。标准解码算法是目前应用最广泛的热图解码算法，它使用高斯滤波器［24］对热图进行平滑后提取响应最大点坐标作为关节点坐标。标准解码算法速度快，但对误差极其敏感，通常精度较低。为了在一定程度上解决这一问题，Newell 等［15］提出了一种基于经验的Shifting 算法，它仅凭借一个点确定关节点位置不够可靠，因此该算法将高斯平滑后热图的最大响应点的坐标向第二最大响应点的坐标移动1/4 的距离以定位人体关节点坐标。该算法由热图的两个极大值代替一个极大值，效果优于标准算法，但由于建立在标准算法的基础上，速度比标准算法稍慢一些。Zhang等［16］提出了一种名为DARK（Distribution-Aware coordinate Representation of Keypoints）的解码算法，该算法在高斯平滑后的热图上取一阶导数和二阶导数求解高斯分布的平均值。由于用到了整个热图的信息，DARK 算法［16］能够提供更精确的预测，是目前精度最佳的热图解码算法，但由于需要进行高斯平滑和求解导数，该算法的速度较慢。以上算法都没有考虑系统误差的影响，因此不可避免地限制了算法的预测精度。

2 本文方法

本章首先回顾热图编码的过程，然后提出本文的误差补偿算法，最后给出误差补偿过程中误差补偿因子的计算方法。

2.1 热图编码

热图编码是将人体关节点坐标转换成对应的热图的过程。在基于热图的人体姿态估计中，人体关节坐标按比例编码到热图中，可以表示为：

p与p'分别对应彩色图中以及热图中的点坐标，λ为神经网络输出步长。最直接的编码方式是将关节点像素设为1，所有的非关节点像素设为0（One-hot 编码）。然而，仅用一个有效像素代表关节点容易受到误差的干扰。相比之下，采用连续的像素分布代表关节点信息更有利于神经网络的学习。用二维高斯分布编码人体关节坐标已经成为一个标准的做法。二维高斯分布可以表示为：

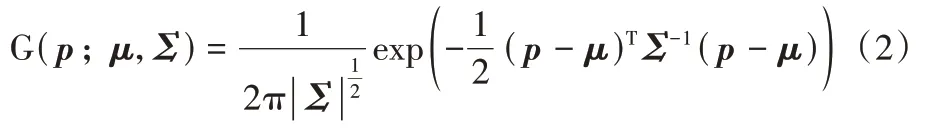
其中：μ为平均值；Σ为协方差矩阵。采用二维高斯编码过后，高斯分布的均值μ所对应的坐标即原来的人体关节点的坐标。解码的过程就是从带有误差的高斯分布中估计均值μ的坐标的过程。

2.2 误差补偿方法

从热图编码的过程可以看出，解码的过程即获得高斯分布均值的过程，标准算法通过最大值所在位置的坐标近似均值的位置，或者采用导数的方法开展更精确的估计，但是现有算法只能平均掉随机误差，无法考虑系统误差的影响。本文提出通过误差补偿的方式，不仅可以消除随机误差的影响，同时充分考虑了系统的作用，并且通过对结果进行补偿修正，能够获取更精确的热图解码。这一节将阐述本文提出的热图误差补偿算法。图1 给出了神经网络预测的热图中存在的误差。针对一维的情况进行分析，所得结论同样适用于二维的真实热图情况。首先，神经网络预测的热图可以分解为：

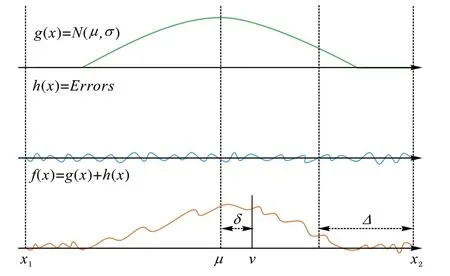
图1 热图的信号和误差函数Fig.1 Signal and error functions of heatmap

其中：g(x)表示高斯分布信号函数；h(x)表示误差函数，同时包含了随机误差和系统误差；f(x)表示神经网络预测的热图，即带误差的信号函数。为便于描述，将f(x)、g(x)和h(x)简单地表示为f、g和h。

解码的任务可以定义为：g和h均未知，f已知，求μ的估计值，下面给出了本文提出的误差补偿算法的理论推导。根据均值的定义，高斯信号g的均值μ可以表示为：

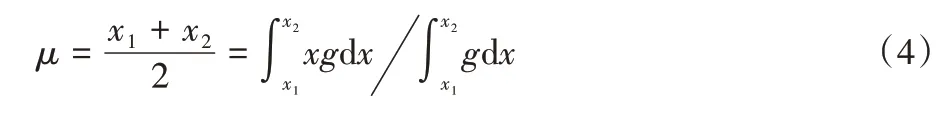
同样地，选取一个较小的偏移量Δ，带噪声的信号f在区间［x1，x2-Δ］的均值ν(Δ)可以表示为：

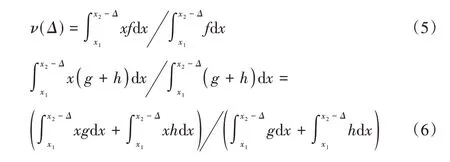
对于一个收敛较好的神经网络，应该具有较高的信噪比，因此在区间［x1，x2-Δ］上误差的积分相较于信号的积分可以忽略，即

将式（7）代入（6），可得

又由于Δ较小且信号g是均值为(x1+x2)2 的高斯分布，其主要响应位于均值附近，所以可以认为g在[x1，x2］区间上的积分远大于在［x2-Δ，x2］区间上的积分：

再由ν(Δ)的定义（5）可知，将Δopt代入式（5）可得待求量μ的一个估计值为：

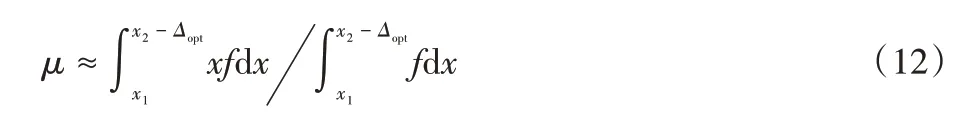
称Δopt为误差补偿因子。

2.3 误差补偿因子的计算

式（12）即本文提出的误差补偿热图解码方法，可以看出μ被近似为f在区间［x1，x2-Δopt］上的平均值，已知Δopt即可得到μ的估计值，下面将讨论如何确定Δopt。由式（10）可以得出，由于误差函数h的不确定性，理论上并不一定存在一个Δopt，使得δ(Δopt)=0 成立，因此需要寻找使δ(Δ)最接近于0 的Δ，即

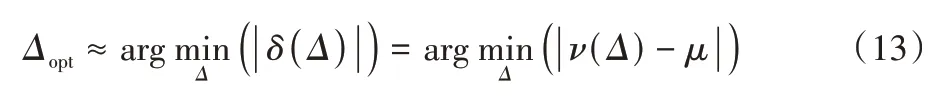
由于μ和Δopt都是待求量，因此不能通过式（13）求解。在实际情况下，可以通过数据集确定Δopt的值，假设算法的精度为A，它可以表示为ν的函数，即A(ν)，在训练集D上评估神经网络N的精度可以表示为：

那么，在理论上A在μ处取得高精度，即

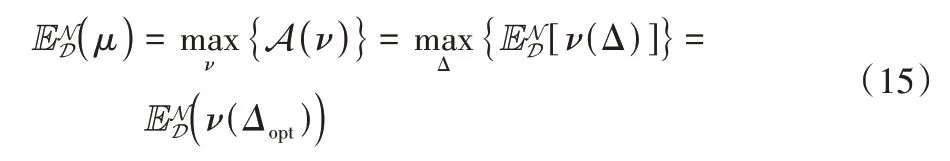
因此，Δopt可以被表示为：

对于二维真实热力图的情况，由于在数据编码、网络推理和热图解码过程中，x和y方向都采用相同处理。因此由对称性可知，x和y服从相同的误差分布，可以得出：

值得注意的是，本文算法一次性补偿所有误差包括随机误差和系统误差。此外，与以往算法不同的是，此算法无需利用高斯光滑进行预处理，因为该算法可以在任意带有噪声的热力图上开展积分运算，噪声本身可以被计算为需要补偿的对象，4.4 节进一步讨论了高斯平滑对不同算法的影响。

3 实验设置

当模型在训练集上收敛后，通过式（16）可获得最优误差补偿因子Δopt。图2 描述了确定Δopt的具体步骤：1）首先找到热图的最大值（图2 中的A 点），近似作为高斯分布的中心位置。2）将积分区域扩展到6σ+3，其中σ是高斯分布的标准差。由于高斯分布落在（［-3σ，3σ］）区域内的概率为99.7%，为了进一步覆盖整个分布，这里在两边再额外扩展一个像素，达到6σ+3。注意，也可以采用更大的区域，对结果没有影响，但是会带来额外的计算。3）将x和y轴的上限减小Δ（在图2 中仅显示x轴），并使用式（5）进行积分，获得预测的关节坐标ν(Δ)，再用式（14）评估模型精度A(ν)（例如，COCO（Common Objects in COntext）上的平均精度）。4）最后再由式（16），获得最佳模型性能的是最佳误差补偿因子Δopt，该误差补偿因子将用于模型推理。值得注意的是，x1和x2的值是由生成热图的σ大小决定的，更大的σ值需要更大的积分区域，即x1=-3σ，x2=3σ。

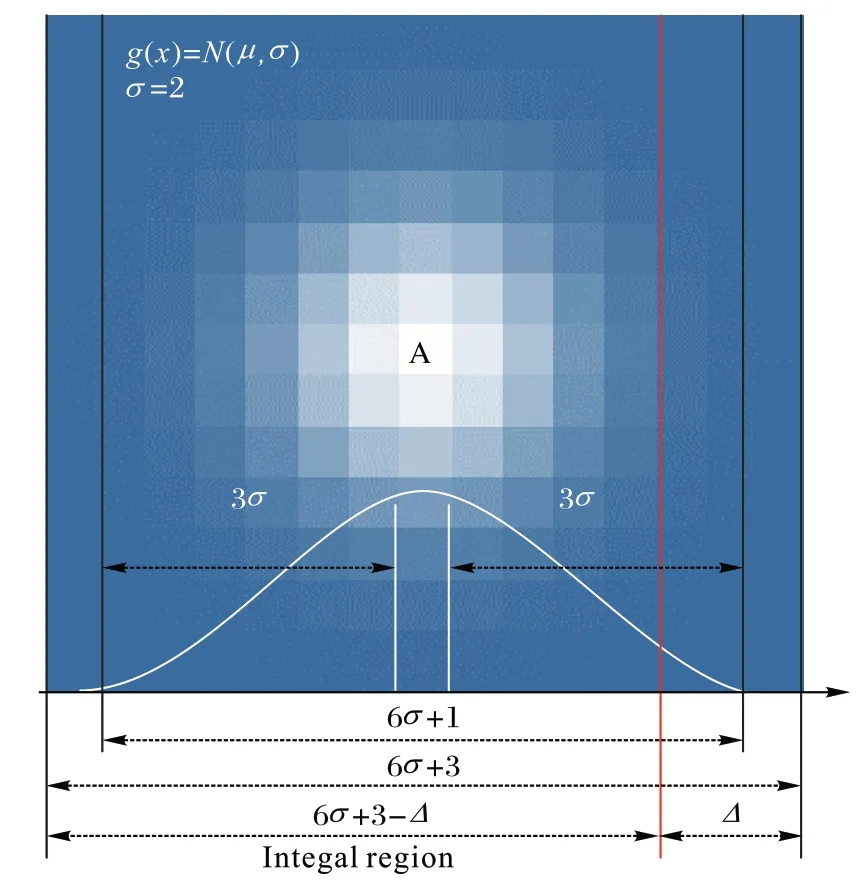
图2 计算最优补偿因子Δopt的方法Fig.2 Calculation method of optimal compensation factor Δopt

本文采用COCO-2017 和MPII（Max Planck Institute for Informatics）两个广泛使用的人体姿态估计数据集进行测试，COCO 关键点数据集［25］具有20 万张图像包含超过25 万个人像样本，这些样本具有丰富的人像尺度、背景环境和遮挡模式。每个人实例被标记为17 个关节。MPII 人体姿态数据集［26］包含2 万张图像，其中包括4 万多个人体样本，每个样本都有16 个关键点。平均精度（Average Precision，AP）和相对头部的正确点百分比（Percentage of Correct Keypoints with respect to head，PCKh）指标分别用于COCO 和MPII 数据集以评估模型性能。

为了开展充分的验证，本文采用14 个模型进行评估，包括 HRNet（High Resolution Net）模型族（HR-W32 和HR-W48）［2］和ResNet 模型族（ResNet-50、ResNet-101 和ResNet-152）［17］，模型具有具有3 种输入分辨率（256×192，256×256 和384×288）。本文使用不同的算法对它们的热图进行解码，包括标准算法、Shifting 算法［15］、DARK 算法［16］和本文算法。值得注意的是，原始的DARK 算法［16］为了提升精度，采用了flip 的策略，但是flip 策略需要进行2 次推理，在实际应用中为了达到较快的推理速度，通常并不会采用flip 策略，因此本文在模型评估中不使用flip 策略。

4 实验结果与分析

4.1 系统误差

表1 列出了各个模型在COCO 和MPII 上的Δopt值，因为在这两个数据集上具有相同的Δopt值，所以没有分别列出。

表1 各个模型的最优误差补偿因子Δopt值Tab.1 Optimal error compensation factor Δopt value of each model

这说明COCO 和MPII 数据具有较高的一致性。另外，对于所有模型都有Δopt＞0 成立，说明系统误差总是向右下角偏移，需要通过减小右下角的积分面积补偿系统误差带来的偏移。本文仅从实验结果中观察到了系统误差，并不能确定系统误差的准确来源，系统误差可能是由于神经网络中的不对称操作造成的，例如非对称pooling，非对称padding 或stride＞1 的卷积等操作，这些操作导致特征向右下角移动，从而引入系统误差。由于这些系统误差不能仅仅依靠热图本身的信息消除，因此标准算法、Shifting 算法［15］和DARK 算法［16］都无法消除系统误差，而本文算法利用了训练集和模型提供的支撑信息，可以起到消除系统误差的作用。

4.2 COCO结果

本文在COCO 数据集上对比了各个算法。表2 列出了各个模型的精度指标，包括平均精度（AP）和平均召回（AR）。可以看出，本文算法在各个指标上都优于其他算法。具体来说，本文算法使HRNet-W48-256×192 模型的平均精度相比之前最佳算法提升了2.86 个百分点。算法的精度可以排列为：本文算法＞DARK 算法［16］＞Shifting 算法［15］＞标准算法。前3 种算法建立在标准算法的基础上，所以精度更高。DARK算法［16］通过充分利用热图信息，能够比Shifting 算法［15］更好地减小随机误差；但DARK 算法［16］仍然存在显著的系统误差，因此精度不如本文算法。

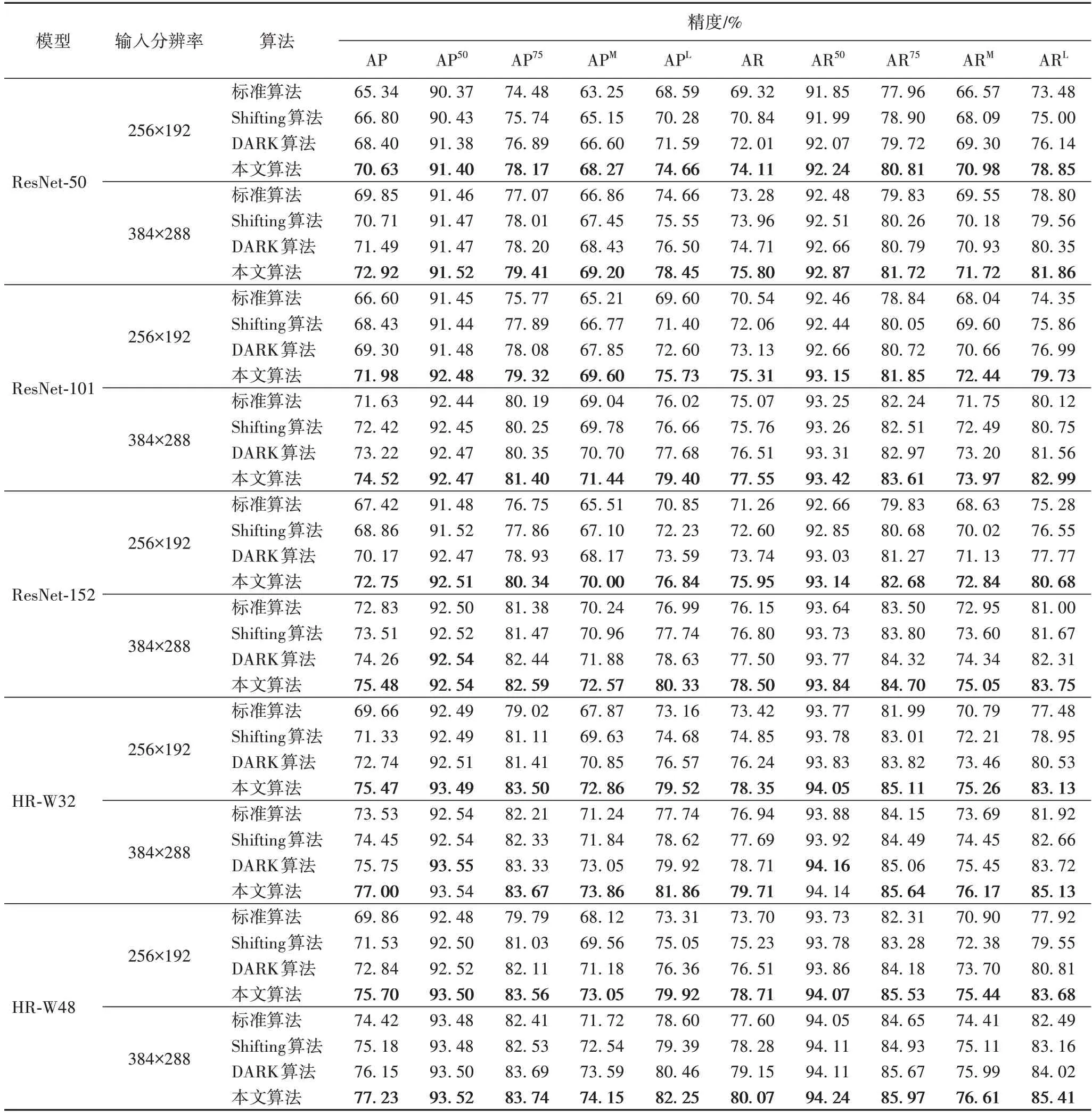
表2 COCO验证集上的精度（验证过程不采用flip策略）Tab.2 Accuracy on COCO validation dataset（validation process without flip strategy）

图3 比较了各个算法的AP 指标。可以看出，相较于对比算法，本文算法获得了较大的精度增益。比如在输入分辨率为256×192 时，本文算法使ResNet-50、ResNet-101 和ResNet-152 模型AP 较之前最先进的DARK 算法［16］分别获得2.24、2.68 和2.59 个百分点的精度提升；HR-W32 和HR-W48 模型的AP 分别提高了2.73 和2.86 个百分点。图4 给出了采用本文算法预测的人体骨架点，蓝色和红色分别表示没有误差补偿和有误差补偿的结果。可以看出通过误差补偿可以预测出更合理的关节点坐标。从热图看出，采用误差补偿修正前的关节点的位置更接近于最大响应处所对应的坐标位置，然而响应往往并非一个理想的高斯分布，而是受到周围因素，如颜色、形状等的影响而具有不规则的形态。采用了误差补偿算法通过积分修正的关节点位置，更充分地考虑全局响应的影响，预测结果更合理。

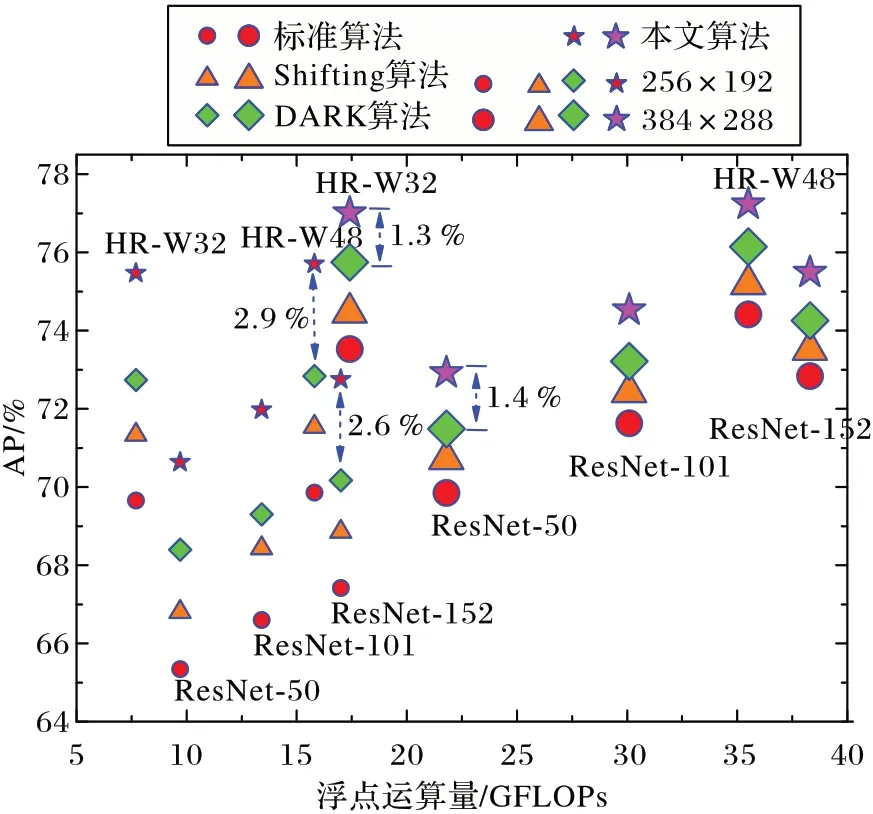
图3 不同算法在COCO验证集上的AP比较Fig.3 AP comparison of different methods on COCO validation dataset

图4 误差补偿对预测结果的影响Fig.4 Influence of error compensation on prediction results

4.3 MPII结果

表3 列出了在MPII 数据集上各个模型的PCKh 值。可以注意到，DARK 算法［16］预测的头部关节更好，本文算法对肩关节、肘关节、腕关节、髋关节和膝关节的效果优于其他算法。图5 对比了不同算法的PCKh0.1（以0.1 为阈值的PCKh指标）和PCKh0.5（以0.5 为阈值的PCKh 指标）指标，同样可以得出：本文算法＞DARK 算法［16］＞Shifting 算法［15］＞标准算法的精度顺序排序。对于PCKh0.1指标，本文算法将HR-W32-256×256 和ResNet-152-256×256 的性能分别提高了8.42 和7.79 个百分点（图5（a））。当使用更宽松的PCKh0.5指标进行评估时，精度提升了0.42 和0.47 个百分点（图5（b））。不同的神经网络结构、输入分辨率、评估指标和数据集的测试表明，本文算法均优于现有的算法，验证了本文算法的合理性和通用性。

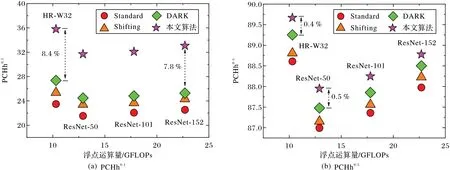
图5 不同算法在MPII数据集上的PCKh值比较Fig.5 PCKh comparison of different methods on MPII dataset

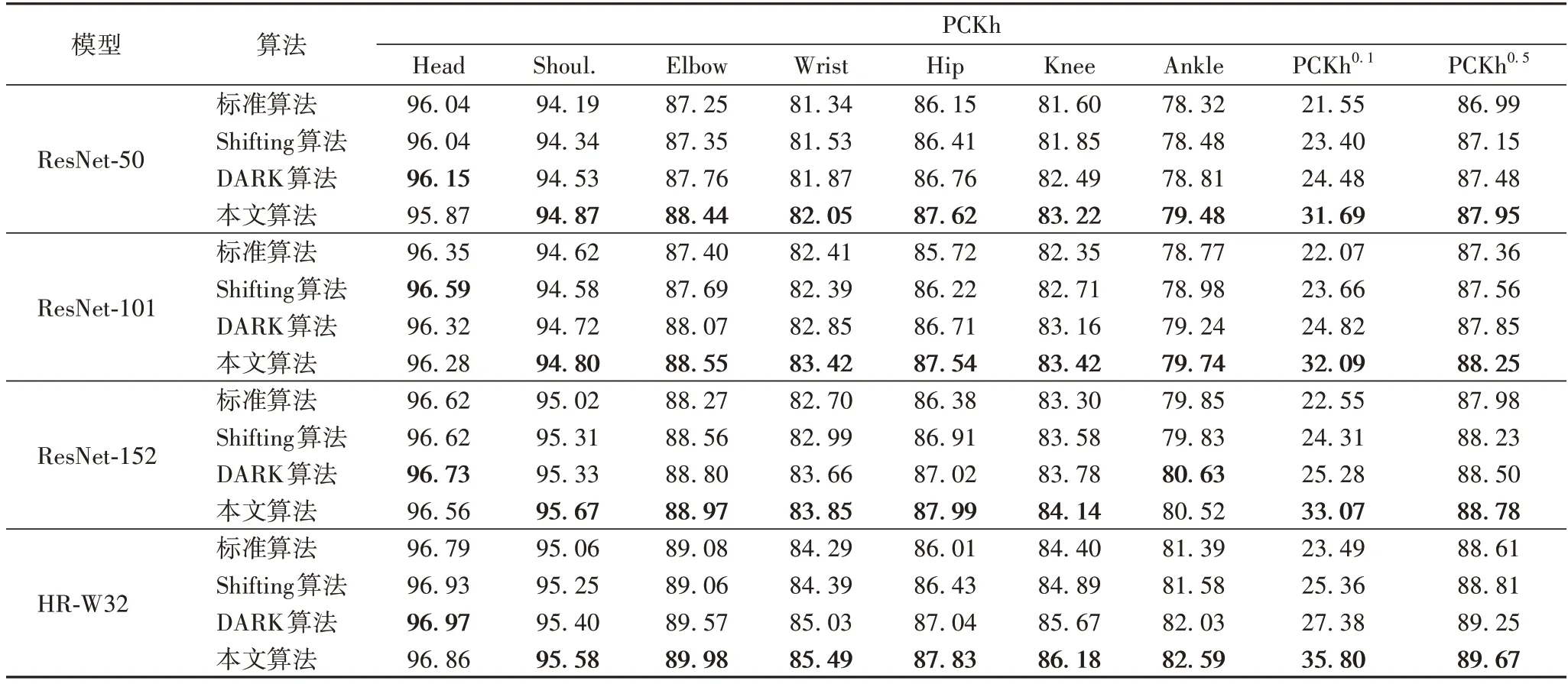
表3 MPII验证集上的PCKh精度（验证过程不采用flip策略） 单位：%Tab.3 PCKh accuracy on MPII dataset（validation process without flip strategy）unit：%

4.4 高斯平滑

以往的算法对高斯平滑有较强的依赖，比如DARK 算法［16］需要用高斯平滑对热图进行预处理，以进行后续的求导操作，不使用高斯平滑会导致明显的精度损失。相反地，本文算法对高斯平滑并没有依赖性，因为本文使用的积分操作对非光滑的表面也适用。表4 列出了高斯平滑对DARK算法［16］和本文算法的影响。可以看出，在没有高斯平滑的情况下，DARK 算法［16］的模型性能显著下降，因为此时DARK 算法［16］不能获得精确的一阶和二阶导数。而本文算法在使用和不使用高斯平滑时，精度仅出现了小幅的波动，表明本文算法并不依赖高斯平滑进行预处理，由于使用积分代替导数，本文算法更能抵抗噪声的干扰。

表4 分辨率、高斯平滑和主干网络对算法精度的影响Tab.4 Influence of resolution，Gaussian smoothing and backbone network on algorithm accuracy

4.5 速度对比

在实际的人体姿态估计应用中，通常要求快速地完成预测，因此算法的速度十分重要。Shifting 算法［15］、DARK 算法［16］和本文算法都是基于标准算法实现的，因此有必要对比各算法所引入的计算耗时。表5 列出了各算法与标准算法相比在Intel Core-i7 9700F CPU 上的额外运行时间。可以看出：Shifting 算法［15］速度最快，但精度低；精度较高的DARK算法［16］处理单张图像需要3.0 ms，这是由于DARK 算法［16］需要进行全图的高斯平滑，然后计算热图的一阶和二阶导数，计算量较大。相比之下，本文算法处理单张图片耗时1.4 ms，速度约为DARK 算法［16］的2 倍，显著地缩短了计算时间。

表5 不同算法相较于标准算法的额外运行时间单位：msTab.5 Extra running time of different methods beyond standard method unit：ms

5 结语

针对当前热图解码算法没有考虑系统误差的问题，本文提出了一种基于误差补偿的热图解码算法。该算法较当前最佳的算法具有显著的精度提升，同时由于不依赖于高斯平滑预处理，不用进行耗时的求导预算，本文算法的速度约为当前最佳算法的2 倍。大量的实验结果表明，当前的人体姿态估计算法的系统误差主要偏向于热图的右下角，可能的原因是神经网络中的非对称操作。当前并不能确定产生系统误差的根本原因，将在以后开展相关的研究。