基于多模态信息融合的时间序列预测模型
2022-08-24吴明晖张广洁金苍宏
吴明晖,张广洁,金苍宏
(1.浙大城市学院计算机与计算科学学院,杭州 310015;2.浙江大学计算机科学与技术学院,杭州 310027)
0 引言
时间序列预测问题研究变量随着时间变化而变化的规律。传统的时间序列预测模型包括移动平均法、指数平滑法、自适应过滤法、自回归模型、差分自回归移动平均模型、状态空间模型等,这些传统模型计算简单,但是对复杂模式的时间序列预测问题解决能力相对较差。比如,张碧琼等[1]使用二重向量自回归模型分析汇率对于股票价格的影响;Contreras 等[2]使用差分自回归移动平均模型预测未来电价。近年来,由于神经网络模型的建模能力更强,可以捕获时间序列内部复杂的模式,所以也逐渐被用于时间序列预测。神经网络模型主要包括前馈神经网络、卷积神经网络(Convolutional Neural Network,CNN)、长短期记忆(Long Short-Term Memory,LSTM)网络等。Gao 等[3]利用股票市场技术指标,使用LSTM 网络模型对股票序列进行拟合。姚小强等[4]提出了一种基于树结构的LSTM 模型,用于预测国际黄金现货交易走势。张栗粽等[5]使用Elman 神经网络模型并融合随机因素优化网络权重,对互联网金融风险进行评估。但是,上述模型仅使用了单因子的数据,由于数据本身的信息量有限,模型的预测结果也因此受到了限制,所以本文使用多模态数据融合的模型进行时间序列预测。
股票价格预测是时间序列预测的经典问题,本文选择股票价格序列作为研究对象。股票价格受到许多因素的影响,序列的随机性比较强,单因子模型较难取得很好的效果,需要更多的外界信息对股票价格序列的预测提供指导。多模态融合旨在提高机器理解多种来源信息的能力,研究如何融合不同模态的信息,形成统一表征,可以弥补单因子模型的缺点。多模态融合的模型不仅可以综合多模态数据中的互补信息,得到更完整的信息表示,也可以提供相同的信息,提高系统的鲁棒性。多模态融合模型包括多核学习、概率图模型、神经网络模型等,其中神经网络的融合效果在很多任务中表现更好。Gao 等[6]使用了注意力机制,提出了一种动态融合多模态特征模态内和模态间信息流的模型,在VQA 2.0视觉问答数据集上取得了当时最优的性能。孔震等[7]使用时间卷积网络(Temporal Convolutional Network,TCN)[8]对未来天气进行预测,使用双线性融合的模型提高了对特征的提取能力。Kim 等[9]使用多模态低秩双线性池化(Multimodal Low-rank Bilinear pooling,MLB)模型提取特征,在VQA 数据集的可视化问答任务中,MLB 模型比原先的双线性池化模型效率更高。Yu 等[10]提出多模态因式分解双线性池化(Multimodal Factorized Bilinear pooling,MFB)模型,MFB 模型对MLB 模型进行改进,将MFB 模型和注意力机制结合,以学习图像和问题之间的关联关系,提高模型在视觉问答问题上的性能。
由于当前的单因子模型预测能力不足,而多模态融合模型的效果仍然有提升的空间,所以本文提出了一种基于全局注意力机制和跳跃连接的多模态融合模型Skip-Fusion,对时间序列进行预测。本文模型综合考虑了股票文本和股票价格两种模态数据,并使用全局注意力机制对多个股票文本的特征进行了融合,充分利用文本中的信息以提高模型的预测结果,模型中的跳跃连接可以捕获多模态数据不同层次的信息,获得更好的多模态融合效果。在真实的股票价格数据集上进行实验,实验结果表明相较于以往的单模态和多模态特征融合模型,本文模型能在股票价格的时间序列预测任务中得到更小的损失和更高的收益。
1 本文模型框架
基于多模态信息融合的时间序列预测模型的模型框架如图1 所示。模型使用任意行业的股票研究报告的文本数据和该行业的股票价格数据两种多模态数据作为输入,训练出可迁移的股票预测模型,可以对该行业股票未来若干天的整体价格走势的均值进行预测。模型由多模态特征的提取与表示以及多模态信息融合的股票价格预测两个模块组成。

图1 本文模型框架Fig.1 Framework of the proposed model
多模态特征的提取与表示模块主要由段落级别的特征提取与表示、词级别的特征提取与表示、股票价格数值的特征提取与表示三部分组成。
多模态信息融合的股票价格预测模块包括输入层、TCN、输出层三部分。输入层和输出层具体结构为前馈神经网络,对于模块的所有层,层与层之间使用了跳跃连接的结构,用于融合多层次的多模态特征。
2 多模态特征的提取与表示
2.1 研报文本特征的提取与表示
研报文本特征包括段落级别和词级别两种特征。段落级别特征指研报文本本身,由于研报标题给出了研报的核心观点、核心事件,所以选择研报标题提取段落级别特征;词级别特征指股评人在研报中给出的股票走势的评级词汇,比如“强于大势”“中性”等。
使用词向量技术提取段落级别的特征,使用BERT(Bidirectional Encoder Representations from Transformers)预训练模型[11-12]的编码器将单个段落表示成文本向量。由于BERT 在训练词向量时,目标训练任务与本文的目标任务并不相同,为了获得泛化效果更好的文本向量,选择编码器第4 层的输出进行平均后的结果作为文本向量表示。
对于某个时间段t中获得的多个研报,形成D份段落文本,每个文本被映射成一个768 维文本向量dit∈R1×768,t时间段对应的文本向量集合表示为:
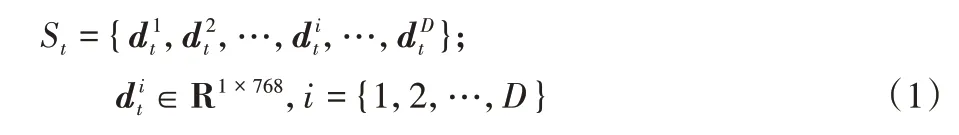
时间序列{1,2,…,t,…,T}对应的段落级别特征矩阵可以表示为文本向量集合按时间顺序拼接:

段落级别特征维度较高,而数值特征是一个简单的数字,所以需要对特征进行降维。使用主成分分析(Principal Component Analysis,PCA)降维方法保留文本特征中最重要的100个特征,单个文本向量∈R1×768被降维成向量PCA() ∈R1×100。
词级别的特征为研报评级词汇,将未指定评级也算作一类评级级别,则研报评级共28种,其他27种评级对应的具体评级词汇包括“持有”“推荐”“看好”“强烈推荐”“优于大势”“弱于大市”“中配”“标配”“增持”“买入”“强于大市”“谨慎推荐”“优异”“优于大市”“Outperform(跑赢大市)”“落后大势”“回避”“中性”“低配”“领先大市”“同步”“超配”“同步大势”“落后大市”“跟随大市”“减持”“同步大市”。
一条研报对应一个评级,对于时间段t内的D条研报,可以获得D个词级别的特征,其中为单个词向量,使用独热编码表示,则时间段t对应的研报词级别向量集合为:
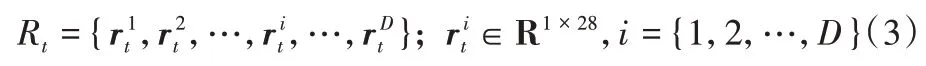
不同时间段的词级别特征序列按时间顺序拼接,得到词级别的特征矩阵:

单日有多个段落级别和词级别的特征,但只有一个股票价格数据,三者难以对齐;并且不同文本对于结果的贡献不同,需要对不同文本赋予不同权重。本文使用全局注意力机制对段落级别特征进行加权,提出全局注意力机制模块,结构如图2 所示。

图2 全局注意力机制结构Fig.2 Structure of global attention mechanism
已知某个时间段t有股票段落级别向量集合St和词级别的向量集合Rt,两者一一对应。使用词级别的评级特征对段落级别特征进行指导,如果评级看涨,则段落级别特征应该预示看涨。本文提出如下基于注意力机制的计算方法,对多个段落级别特征的权重进行计算:

首先将单日多个段落级别、词级别的向量拼接成矩阵,段落级别的特征矩阵Concat(St)维度为D× 100,词级别特征矩阵Concat(Rt)维度为D× 28。初始化一个维度为100 × 20的可训练矩阵WS和一个维度为28 × 20 的可训练矩阵WR,分别将段落级别和词级别的特征矩阵与WS、WR相乘,将相乘得到的两个矩阵进行哈达玛积,得到注意力矩阵ASR。然后对注意力矩阵进行正则化、最大池化操作,得到一个D维的权重向量,使用Softmax 操作对权重向量归一化,得到最终的权重向量ΑW={w1,w2,…,wd,…,wD}。
使用权重对单日多个段落级别向量进行加权,得到多文本融合的单一向量表示:

全局注意力矩阵的值通过预训练固定下来,预训练将文本与股价涨跌关联起来,输入某个时间段的段落级别和词级别向量,通过注意力机制加权后,以该时间段的涨跌为目标,1 表示涨,0 表示跌,训练注意力机制的权值。训练完成后,直接使用训练好的注意力矩阵获得段落级别的多文本融合的向量表示。
单日的多个词级别的特征也需要进行融合,以方便与单日的价格特征对齐,使用平均池化进行融合,得到一个28 维的向量:
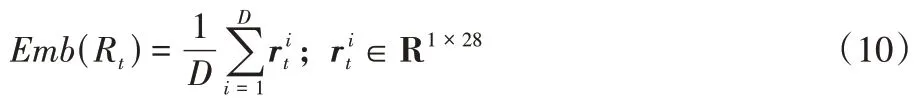
2.2 数值特征的提取与表示
对于数值数据,按时间顺序进行拼接,得到数值序列。数值特征选择股票价格的每日收盘价格,股票每日收盘价格是股票市场当日收盘前一段很短时间的交易价格的加权平均,是很常用的指示股票市场价格变化的指标。
将第t天的收盘价格表示为pt,则时间序列{1,2,…,t,…,T}对应的股票价格序列为:

使用移动平均值(Moving Average,MA)的方法进行数据平滑,减小序列中的噪声。已知对于股票价格序列PT,选择平滑窗口大小为5 个交易日,则第T天的股票价格的移动平均值为:

将不同日期的移动平均值按时间顺序相连,得到移动平均线。移动平均线是股票市场中很重要的参考指标,收盘价的移动平均线能够很好地反映股票价格变动的趋势。股票价格的移动平均线可表示为:

股票价格可能存在数据偏移的问题,比如由于股票不断上涨,导致训练时数据基本集中在20 元左右,预测时数据却集中在200 元左右;或者发生股票分割时,股票价格由200 元每股分割为10 元每股。为了消除数据偏移的影响,需要对数据去趋势化。
使用均值去趋势化解决数据偏移问题,均值去趋势化计算股票价格序列的均值,用股票价格减去均值,得到去趋势化的序列:
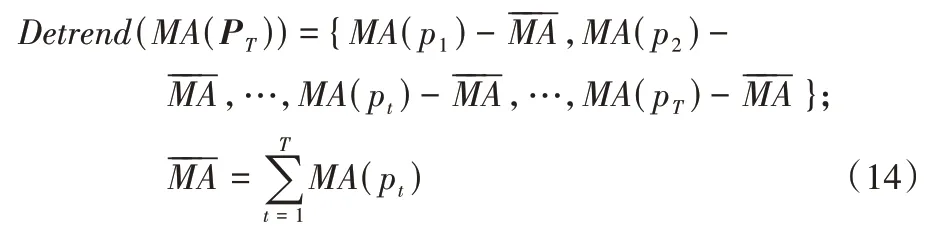
3 多模态信息融合的股票价格预测
3.1 股票价格预测模块具体结构
将段落级别向量序列、词级别向量序列、数值序列按时间对齐、拼接,得到股票价格预测模型的输入。对于序列中的某一天t,段落级别和词级别的两种文本特征进行拼接,得到文本特征Concat(Emb(St),Emb(Rt)) ∈R1×128,数值特征为pt∈R1×1,假设共有T天的数据,则文本特征按时间顺序可以拼接得到T×128维的矩阵,数值特征得到T×1维的矩阵。
本文模型的输入层由前馈层组成,用于对输入进行线性变换,对输入的浅层特征进行提取。经过变换,由Concat(Emb(St),Emb(Rt))得到向量Ct∈RC×1,由pt得到向量Vt∈RV×1。将前馈神经网络的输出、数值输入数据,按时间对齐拼接,得到后续TCN 的输入:

使用卷积神经网络的变体TCN 进行多模态特征融合。TCN 模型由若干相同的层组成,每个层包含两个相同子层,子层包含空洞因果卷积层、权重归一化、线性整流函数(Rectified Linear Unit,ReLU)、Dropout 层四部分,每个层上使用残差网络的结构。
本文对TCN 的激活函数进行了调整,将线性整流函数替换成了Sigmoid 函数。因为去趋势化后的股票价格可能为正也可能为负,而线性整流函数将负值的输入直接映射为0,相当于让负值股票价格直接失效,并不适用于股票价格预测。
TCN 的输出表示如下:
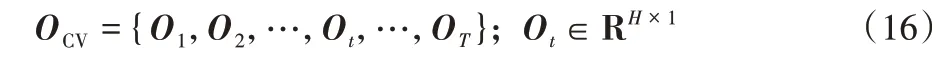
其中:H表示TCN 最后一层输出通道的大小;Ot对应时间段t经过输入层和TCN 后得到的特征。
本文模型的输出层也是一个前馈网络,用于预测结果。将数值输入、数值数据的前馈层输出、TCN 的输出按时间对齐,拼接成向量,使用前馈网络计算,WF和bF为前馈网络的权重与偏置值,计算得到维度为1 的预测值:

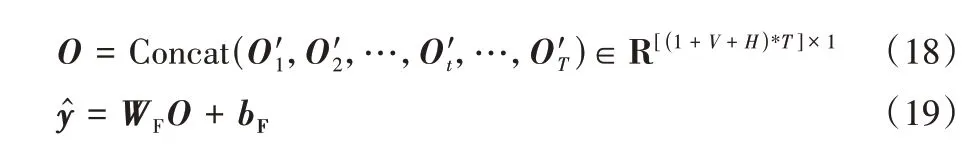
3.2 跳跃连接
由于不同模态数据的浅层特征和深层特征对结果的贡献并不相同,使用跳跃连接的结构对多模态数据不同层次的特征进行融合以达到更好的融合效果,本文的跳跃连接表示成如下数学形式:
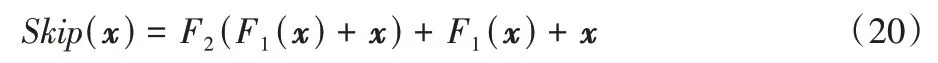
公式分为x、F1和F2三个部分:x表示输入,包含最浅层的特征;函数F1对输入进行特征提取,得到浅层特征;将前两者相加,通过函数F2处理得到更深层次的特征。将前三者相加得到跳跃连接的输出。
本文的跳跃连接和残差连接的结构相似,但是本文的跳跃连接的每一层都使用到了之前所有层的直接输出,所以是一个层与层之间前向全连接的结构。当网络深度增加时,公式可以进行递推,让每一层使用前面所有层的输出作为输入。如图3 所示,假设共有L层,每一层对应的函数为FL,Norm 表示正则化操作,则递推公式为:

图3 跳跃连接Fig.3 Skip connection
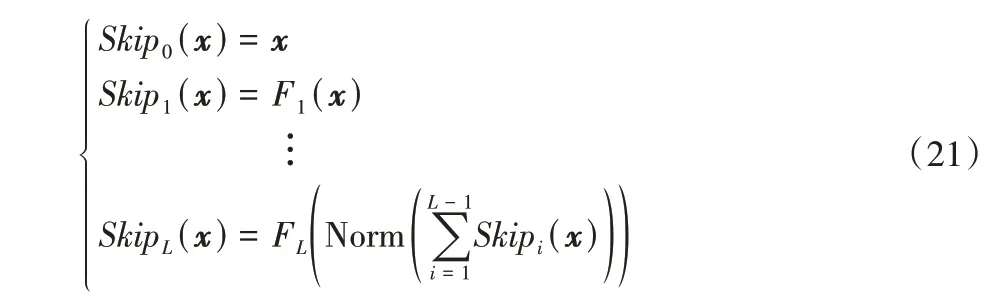
其中FL函数根据不同任务的特点选择不同的形式。比如,在图像处理中,FL通常可以取全连接层、卷积层等处理方式,在自然语言处理中,FL通常可以使用Seq2Seq(Sequence-to-Sequence)系列的模型提取特征。
4 实验与结果分析
4.1 数据获取
选择东方财富网上的医疗行业研究报告数据,以及国泰安CSMAR 数据库(China Stock Market &Accounting Research Database)中医疗行业的12 只股票每日收盘价格数据构建数据集。
在股票价格预测中,为了获得更加中立的研报数据,选择使用行业研报作为具体信息源。行业研报体现了专业人员对于某个行业发展趋势的总体把握,与具体股票无关,所以可以不受具体企业的影响,更加中立地判断。选择预测未来若干天股票价格走势的均值是由于股票波动性大,而研报内容通常和未来若干天的股票价格变化有关,所以预测未来一段时间的股票价格而非具体某一天的走势更为合理。
通过爬虫技术对东方财富网的研报进行爬取,获取到2018年10月30日至2020年10月29日共71915条研报数据,过滤非医疗行业的研报,共获得4 171 篇医疗行业研报文本,如表1 所示。由于研报标题和评级词汇能够表明研报的主题和作者态度,选用这两部分作为多模态融合的文本数据。对研报数据进行预处理与文本清洗,对标题文本删除停用词、标点,对评级词汇进行去重和统计。

表1 研报数据示例Tab.1 Examples of research report data
股票价格数值从CSMAR 数据库获取,获取了12 只医疗领域的股票的日收盘价格,时间跨度为2018 年10 月30 日至2020 年10 月29 日。12 只医疗领域的股票分别为国际医学、迪安诊断、宜华健康、创新医疗、爱尔眼科、美年健康、光正眼科、览海医疗、通策医疗、盈康生命、泰格医药、金域医学。
由于股票开盘日期和研报发布日期并不完全一致,所以对股票开盘日期和研报发布日期取交集,保证获取到的每日数据有意义。处理后剩余471 日的数据,将数据按时间顺序排序,前300 日的数据作为训练集,后171 日作为测试集。
使用滑动窗口的方法构造数据集。首先确定一个采样时间窗口T和采样时间间隔λ,然后从某个时间点起始,在之后大小为T的时间窗口内,每隔时间间隔λ采样一次,每次采样获得当时的股票收盘价格和若干份研报文本,最后得到长度为的股票价格序列和研报序列。历史序列的时间窗口T取30 日,采样时间间隔λ取1 日,使用历史序列中30日的股票价格和研报序列对未来进行预测,预测目标是未来5 个交易日股票价格的均值。
数据集包括12 只股票在471 个交易日的数据,一共有5 652 条数据,使用构造出的数据集,训练了一个可以对行业股票总体走势进行预测的股票价格预测模型。
4.2 评价指标
使用均方根误差(Root Mean Square Error,RMSE)对模型进行训练,使用均方根误差、可决系数(R-Squared)以及日收益(Daily Return,R)来评估模型。
均方根误差表示预测值与实际值之间的偏差,公式如下:
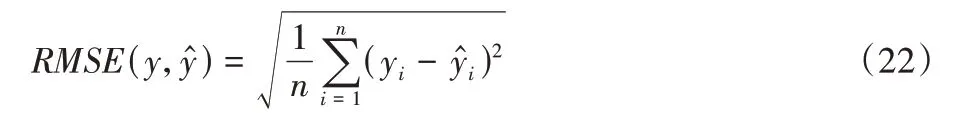
可决系数用于评估模型的拟合优度,公式如下:

日收益表示下一日相对当日能获得多少收益,它衡量了模型指导股票购买的实际盈利能力。本文对这个计算公式作出一些调整,使用未来5 日的股价均值替代下一日的股价。假设第t日股票价格为pt,未来5 日股价均值为pt+1:t+5,模型预测的未来5 日的股价均值为。当预测值比当日上涨,则买入,收益为未来5 日股价均值减去当日实际价格;反之不购买,日收益为0。计算公式为:

4.3 基准模型和参数设置
为了验证本文提出的模型的效果,将它与其他单模态和多模态融合的模型进行比较。
单模态的模型选取了6 种:1)朴素预测法(Naïve),使用当天收盘的价格作为未来的预测值;2)移动平均法(MA),使用当天及之前若干天价格的平均值作为未来的预测值;3)指数移动平均法(Exponential Moving Average,EMA),使用当天及之前若干天价格的加权平均值作为未来的预测值;4)差分自回归移动平均(AutoRegressive Integrated Moving Average,ARIMA)模型,它是自回归模型的一种,对于不平稳序列,ARIMA 会使用差分法对序列平稳化,使用移动平均法进行数据平滑,然后使用自回归模型捕获序列变化规律;5)门控循环单元(Gated Recurrent Unit,GRU)模型[13],是LSTM 模型的变体,具有重置门和更新门两个门结构,在保持LSTM 效果的同时,使得计算变得简单;6)TCN 模型[8,14],是CNN 的变体,对长序列的处理能力更强,也更适用于时间序列的预测。
多模态融合的模型选取了4 种:1)拼接(Concat),直接将多模态数据拼接来进行多模态融合;2)哈达玛(Hadamard)积,将多模态数据的特征矩阵进行哈达玛积运算,进行特征融合;3)MLB[9,15],是双线性模型的一种,使用一个矩阵Wi对两种模态的输入x和x′进行融合,使用矩阵分解的方法将Wi分解为两个维度为1 的低秩矩阵Ui和,得到一个输出特征,◦是哈达玛积,不同的矩阵Wi对x和x′融合可以得到不同输出特征,将不同输出特征拼接,得到多模态融合特征;4)MFB[10,15],类似MLB 模型,与MLB 的区别在于,分解所得的低秩矩阵的维度大于1,所以得到的输出特征为zi=,此处Ε表示一个全为1 的矩阵。
实验中,单模态模型选择调参结果最优的模型。多模态融合实验只改变多模态融合模型,不改变输入以及模型参数,多模态融合模型的参数设置见表2。
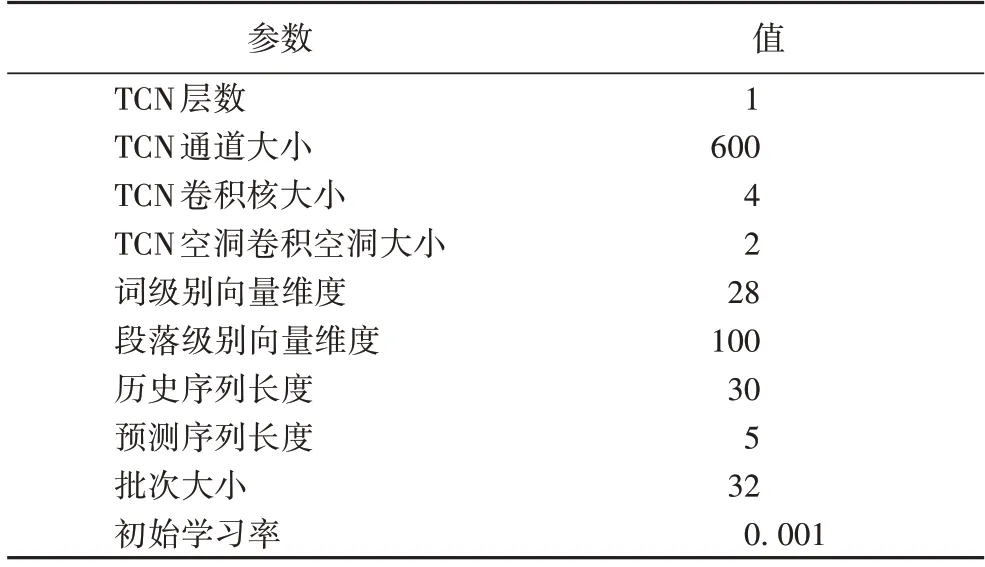
表2 多模态融合模型的参数设置Tab.2 Parameter setting of multimodal fusion model
4.4 实验与结果分析
实验得到的测试集的实验结果如表3 所示。本文提出的Skip-Fusion 模型在RMSE 上获得了最好的结果,在RSquared 上也得到了比较高的分数,尤其是在日收益(R)上获得了最好的结果,表示本模型相比其他模型能更好地指导股票交易,并获得实际收益。
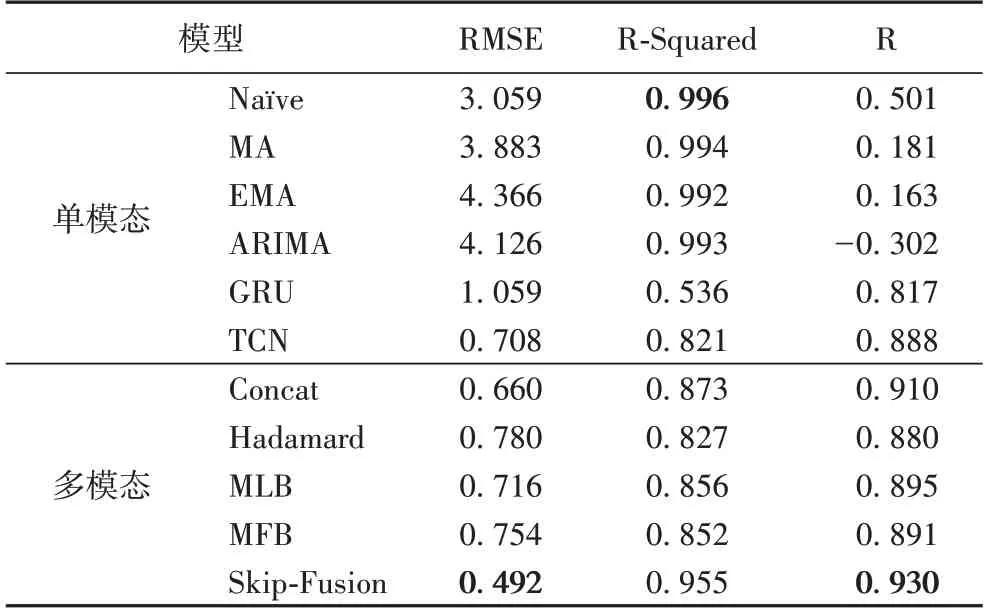
表3 单模态和多模态融合模型实验结果Tab.3 Experimental results of single-modal and multimodal fusion models
Naïve 模型、MA 模型、EMA 模型、ARIMA 模型4 个传统模型在R-Squared 上得到较高的分数,表示它们可以较好地对曲线进行拟合,但是它们的RMSE 很高,R 也很低,说明这些模型虽然可以对结果进行拟合,但是却无法指导实际的股票交易。
除了上述四个模型,GRU、TCN、Concat、Hadamard、MLB和MFB 模型在RMSE、R-Squared、R 三个指标上可以获得较低的损失,也有较高的拟合优度和日收益,可以用于指导股票交易,但是Skip-Fusion 模型与这六个模型相比,在三个指标上都获得了最好的结果,其结果更具指导价值。
本文提出的Skip-Fusion 模型与Concat 模型非常相似,在输入层对文本和数值特征都采取拼接的方式融合了浅层特征,两者的主要区别在于Skip-Fusion 增加了跳跃连接的结构对多模态数据进行多层次的信息融合,说明使用跳跃连接可以更好地利用多模态数据,提高模型预测的准确率和可靠性。
单模态的TCN 模型和所有多模态融合模型中,都使用了TCN 模型用于股票价格预测,但是相较于单模态的TCN 模型,多模态融合模型中的Concat 模型和Skip-Fusion 模型在三种评价指标上都获得更好的结果,表明多模态数据可以提升预测结果,但是仍然需要选择出合适的多模态融合模型,才能够充分利用多模态数据的信息。
本文对模型运行的时间复杂度也进行了分析。已知输入的文本特征为T× 128 维的矩阵,数值特征为T× 1 维的矩阵。GRU 与TCN 模型的层数均为1,GRU 的隐藏层单元数为HGRU,TCN 的隐藏层通道数为HTCN,MLB 和MFB 提取特征的矩阵个数都为HM,MFB 矩阵分解的秩为K,输入层的前馈网络的隐藏层单元数HF,输出层的前馈网络隐藏层单元数为1,则时间复杂度如表4 所示。
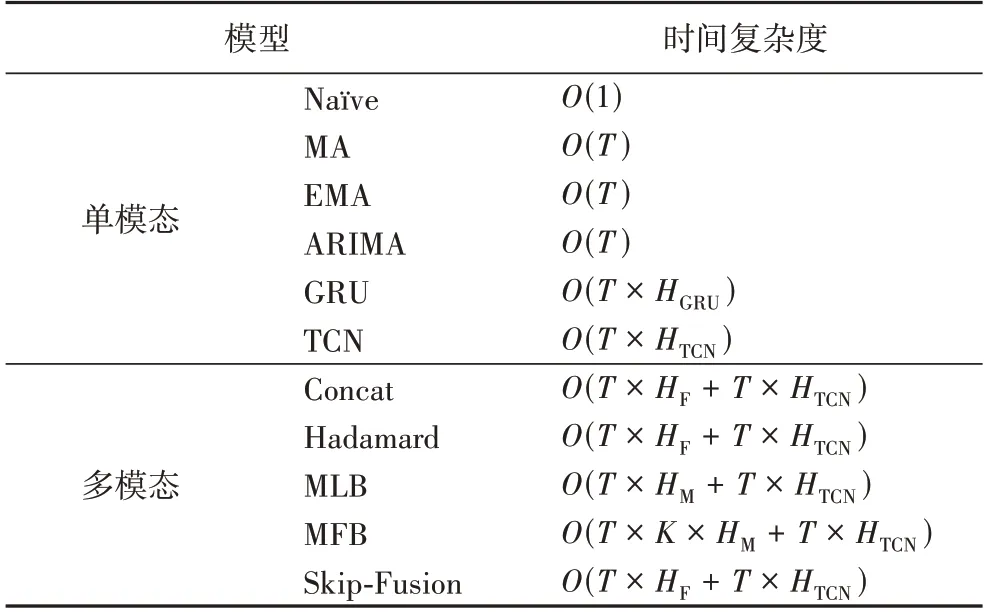
表4 时间复杂度分析Tab.4 Time complexity analysis
可以发现单模态模型的时间复杂度相对较低。由于HF、HM、K取值一般处于同一个数量级,在100 以内,所以多模态融合模型中,除了MFB 计算量相对较大,其他模型的时间复杂度并没有显著差别。可见,本文提出的多模态融合模型相较于其他多模态融合模型,可以在不提高时间复杂度的情况下改善股票价格时间序列预测的结果。
基于以上分析,在进行多模态融合的时间序列预测任务时:如果数据比较简单,不需要使用较深的网络进行建模时,使用基于拼接的多模态特征融合模型就可以得到比较好的结果;当需要使用比较深的网络时,可以使用预训练模型预先提取出数据内在关联,然后使用基于跳跃连接的多模态特征融合模型融合不同层次的数据特征,达到提高预测能力的同时不增加运算复杂度的效果。
5 结语
本文提出了一种基于多模态信息融合的时间序列预测模型Skip-Fusion。针对单因子模型预测能力不足,多模态融合模型的预测能力仍有待提升的问题,提出了全局注意力机制和跳跃连接相结合的模型框架,全局注意力机制的预训练模型对多文本特征进行融合,获取数据内部特征相关关系,跳跃连接的结构可以对多模态数据不同层次的特征进行融合。在股票价格时间序列预测问题上进行实验,相较于以往单因子和多模态融合的模型,本文模型可以在不增加时间复杂度的基础上,提高预测准确度和可靠性。
