人教版和北师大版数学教材例题设计的比较——以小学高年级为例

文∣林芝兰 伍晓琪 黄甫全

《中共中央关于制定国民经济和社会发展第十四个五年规划和二○三五年远景目标的建议》提出，“十四五”时期要全面贯彻党的教育方针，深化教育改革，建设高质量教育体系。2021年全国教材工作会议也提到，要加快建设高质量教育体系进程，以全面提高教材质量为重点，打造适应时代要求的精品教材。由此可以看出，在建设高质量教育体系进程中，全面提高课程质量尤其是教材质量显得至关重要。

小学数学教材主要由正文、例题和习题构成。其中，例题作为重要构成之一，能够向学生传递数学知识的内涵，引导学生探索数学规律，为学生演示问题解决过程，是将所学知识转化成自身能力的重要脚手架。[1]许多研究者开始关注数学教材中例题的重要地位。基于此，本文从知识领域分布、结构设置、问题表述、难度水平等四个方面对人教版和北师大版教材例题设计进行分析与比较，以期为教材例题的编写和教育教学提供参考和改进建议。

一、研究设计

(一)研究对象

小学五、六年级是学生进入初中数学学习前十分重要的过渡期，而初中数学内容对学生的逻辑思维能力和运算能力要求较高。因此，研究小学高年级数学教材的例题编排，不仅能从比较研究中得到启示，也能与初中数学学习要求相联系，更好地探究数学教材编写如何实现学生学习水平衔接的适切性。本文选取人民教育出版社、北京师范大学出版社2013年出版的小学五、六年级的数学教材共8册，以其中全部例题为研究对象。

(二)研究方法及过程

本文主要采用内容分析法，对人教版和北师大版五、六年级教材的每一道例题进行分析，按照以下三个步骤操作。

1.确定一道例题的划分标志

2.构建分析框架

在已有研究基础上，结合课程标准对教材编写的要求和建议，构建包含例题的知识领域分布、结构设置、问题表述以及难度水平等比较维度的文本分析框架，如表1所示。

表1 小学数学教材例题的比较框架

表2 数学例题综合难度模型

在例题的难度水平方面，王建磐和鲍建生在2014年提出了数学习题综合难度模型。[3]而阳宇茜在对中国、新加坡两国的初中教材例题进行比较时完善了该难度模型。她认为数学例题不能脱离情境而存在，因此将王建磐等人的数学习题综合难度模型的“背景”因素改为“情境”因素，其中的“无背景”水平改为“数学情境”水平。[4]该模型是本文比较例题难度水平的主要研究工具，修正后的数学例题综合难度模型如表2所示。

3.编码标准说明

在对例题进行编码分析过程中，首先由两位研究者依据比较框架对同一单元的例题进行独立的编码分析，对照分析结果讨论并协商。然后邀请第三位研究者对同一内容进行编码，对编码不一致的部分由三位研究员进行讨论，最终确定统一的编码标准。最后，依据确定的编码标准对8册教材的研究数据进行统计、分析，结合教师提问的课堂情境考查，得出研究结论。

二、研究结果

人教版和北师大版的五、六年级的教材中例题共计545道，其中人教版教材包含例题193道，占所研究例题的35.4%，北师大版教材包含例题352道，占全部例题的64.6%。

(一)例题所属知识领域的数量分布比较

人教版教材的例题分布在数与代数、图形与几何、统计与概率、数学思想方法等四个知识领域的数量分别为111道、65道、7道、10道，北师大版教材例题在四大知识领域的数量分布为147道、139道、27道、39道。

可见，在不同版本的数学教材中，四个知识领域的例题所占比例各不相同，人教版在“数与代数”中的例题占比高于北师大版，为57.5%；而北师大版教材在“图形与几何”“统计与概率”“数学思想方法”中的例题占比均高于人教版，分别为39.4%、7.7%和11.1%。尽管如此，人教版和北师大版不同领域的例题编排还有一些相似的特点。第一，分布在“数与代数”中的例题占比最高，在40%以上；第二，“数学思想方法”中也有一定数量的例题，占例题总数的9%；第三，“统计与概率”中的例题占比都是最低的。

(二)例题结构的比较

从例题的结构设置上看，人教版数学教材的193道例题在六大类结构中分布较为均匀，而北师大版的352道例题则在六大类结构中分布差异较大，其中出现最多的结构是“问题+解答”。北师大版的数学教材虽然例题数量多，但将近50%的例题都只采用了“问题+解答”这类较为单一简单的结构，不能很好地发挥例题的启发和示范作用。同时，北师大版的例题在LC5和LC6两类例题结构中分布较少，分别只占了北师大版例题的6.0%和12.2%，需要进行适当的变化，实现例题形式和功能上的改进。而在人教版的教材中，LC6的例题结构占比高达23.8%，尤其是利用新知识解决应用问题时多会设置LC6的例题结构，如人教版五年级上册16页例题。

在解题分析过程中，人教版的例题会将题目中的条件进行适当解释，分析已知和求解的联系，启发学生获取解决问题的思路和方法。最后通过小精灵的引导，进行解题过程的总结与反思，呈现了比较完整的例题结构。事实上，教材中不同功能的例题应该采用合适的结构，对于综合性较强的应用题解题步骤可以加入总结性内容，使学生的学习取得事半功倍的效果。

(三)例题的问题表述

例题的问题表述特征包含了“提出问题的句式”和“提出问题的类型”两个方面。不同的问题表述方式能够在一定程度上体现数学例题的设计特点。

1.例题提出问题的句式

两个版本的545道数学例题中，问题句式为陈述句的例题有165道，占例题总数的30.3%；问题句式为疑问句的例题有380道，占例题总数的69.7%。人教版和北师大版数学教材中例题提出问题的句式为疑问句的例题占比均接近70%。这表明，疑问句是教材例题设计的主要问题句式，旨在激发学生主动思考和积极探索的数学学习意识。两个版本数学教材在例题提出问题的句式设计上所占比重较为相似。例题中不同的问题句式指向相应的课堂教学活动，是教师进行教学活动设计的重要依据。多样的教学活动能让学生在小组合作中发展协作交流的能力，获得多样的数学活动经验。

2.例题提出问题的类型

在人教版和北师大版数学教材的545道例题中，有316道例题提出的问题为封闭型问题，占例题总数的58.0%；有229道例题提出的问题为开放型问题，占42.0%。其中北师大版教材的封闭型问题和开放型问题所占比例相近，分别为46.5%和53.5%；而人教版教材中，封闭型问题占例题总数的比例高达78.8%，开放型问题只占21.2%。这表明，北师大版教材在例题的设计上更注重问题的开放性，其编排更能够激发学生的学习积极性，培养学生创新思维，较好地融入了“教学活动是师生积极参与、交往互动、共同发展”的课程理念。

(四)例题难度五因素的比较

以数学例题综合难度模型为研究工具，对两个版本小学数学教材中的例题的难度五种因素进行编码，根据表2中的难度因素及划分的不同水平给予赋值；再利用下列公式进行计算得到每个因素上的加权平均值di。

①

其中，dij表示第i个难度因素中第j个水平的权重，之后采取等级权重进行赋值；nij表示的是每版教材中属于第i个难度因素中的第j个水平的例题个数，n则表示每版教材的样本总数。[11]且对于任意的i，都有②式。

∑fnij=n(i=1,2,3,4,5;j=1,2…)

②

经过统计、分析后得到的例题难度五种因素在其难度因素上的加权平均值分布如表3所示。

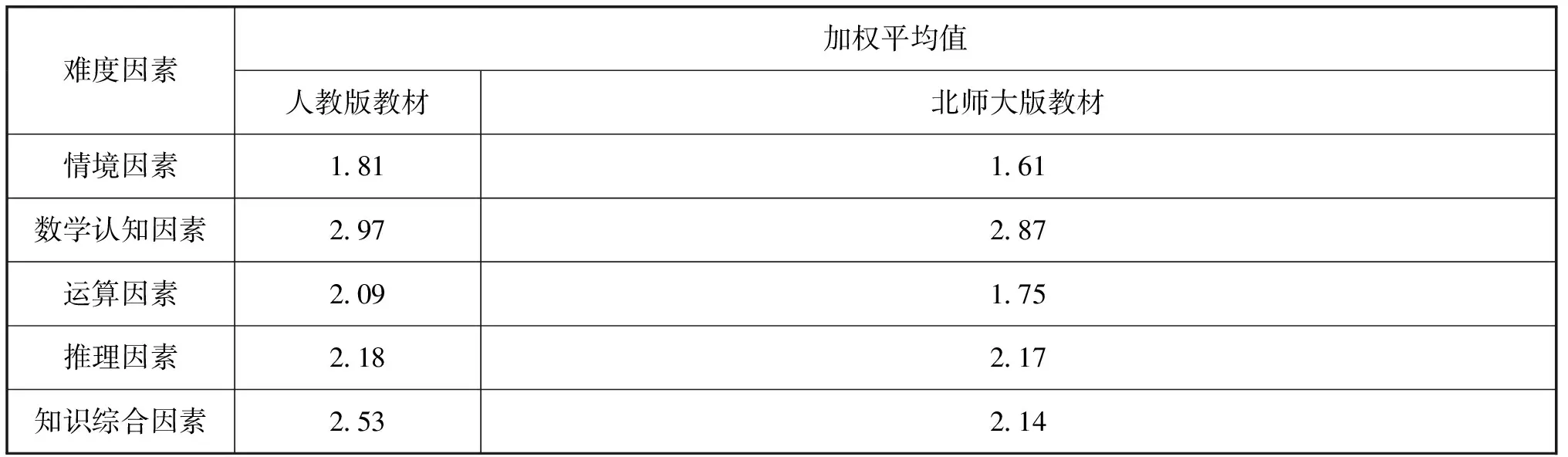
表3 两版本教材数学例题综合难度因素的量化指标统计

本研究分别对五种难度因素进行量化，对人教版和北师大版数学教材中的例题难度特征进行了比较，计算所研究的例题在各难度因素上的加权平均值，并据此作出了人教版和北师大版例题综合难度比较雷达图，如图1所示。

图1 两版本教材数学例题综合难度比较雷达图

从图1可以看出，人教版数学的教材例题在情境水平、运算水平、知识综合水平上均高于北师大版的教材例题，而在数学认知水平和推理水平上与北师大版教材例题相差不大。从图形的整体态势来看，人教版的数学例题在五个难度因素上的整体态势相对来说较为平衡，而北师大版教材例题的情境水平和运算水平偏低。不过，两个版本的教材例题对应的图形都有横向延伸的趋势，说明两版教材对学生的综合运用知识能力和认知能力发展较为重视，但是例题的情境水平都偏低。

三、研究结论与改进建议

(一)研究结论

通过对人教版和北师大版小学数学教材例题设计特点的比较研究，得出了以下结论。

1.在所属知识领域上，两版教材中数与代数领域的例题占比最多

人教版五、六年级的教材在数与代数、图形与几何、统计与概率、数学思想方法四大知识领域的分布比例分别为57.5%、33.6%、3.6%和5.1%；北师大版教材在这四个知识领域中的分布比例分别为41.7%、39.4%、7.7%和11.1%。数与代数作为方程与不等式、函数学习的基础，对学生的数学能力的发展有着重要的作用，这也是数与代数领域例题占比最多的原因之一。

2.在结构设置上，北师大版教材中多层次结构的例题占比偏低

通过对人教版和北师大版的小学数学高年级教材例题进行数据统计及对例题结构设置进行分析，发现人教版小学数学教材例题中含“问题+分析+解答+总结”(LC6)的比重稍高一些，为23.8%；而北师大版小学教材例题为多环节结构的占比偏低，其中LC6阶段最少，只占例题总数的5.9%。在例题中增加多层次的例题结构有助于学生更好地掌握数学知识，也能培养学生良好的审题解题习惯。

3.在问题表述上，都以疑问句式为主，但人教版例题的开放性偏低

研究发现，两版教材的例题提出问题的句式更多是疑问句，占例题总数的69.7%。由此看出，教材试图通过“疑问句问题”来激发学生的求知欲和学习兴趣。在问题提问类型上，北师大版教材中开放型问题所占比例为53.5%，而人教版教材中开放型问题占比只有21.2%。可见北师大版教材在问题开放性上做了更多的尝试和设计，而人教版教材的数学例题整体上开放型问题设置得较少。

4.在难度水平上，两版教材例题的情境水平偏低

通过对人教版和北师大版小学数学高年级教材例题中五种难度因素的统计与分析，我们可以发现，人教版数学教材例题在情境水平、运算水平、知识综合水平上较好，在数学认知水平和推理水平上与北师大版教材例题相差不大。不过，两个版本的教材例题相对来说更注重培养学生的综合运用知识能力和数学认知能力，设置的例题情境水平则明显偏低。

(二)改进建议

从研究结论上看，我国人教版和北师大版的教材例题在不同维度的设计上存在共同点，也有不同侧重点，具有一定的启示作用。因而本文提出以下几点小学数学教材例题编写的改进建议。

1.提高含总结环节的例题比重

在上述研究的教材例题中，两个版本教材的结构中设置有总结环节的例题占比分别为50.1%(人教版)、25.4%(北师大版)。很显然，北师大版数学教材不够重视解题后的回顾与总结。心理学研究表明，如果在呈现样例的基础上增加主要步骤，说明能够在一定程度上提高样例学习的有效性。[5]在教材例题的编排中，应该重视例题的概括和小结，帮助学生建构起较为完善的数学知识体系。将其放在解答前详细的步骤分析，能够起到把相关的信息和知识整合到一起的作用，为整合和保持更为详细的材料提供了理论支架；而在解答之后的步骤总结则回顾了材料，突出重要概念的作用，能够提供更有内聚力的组织框架。[6]

在数学课堂教学实践中，如果讲解完详细的解题过程后教师没有进行及时回顾总结，大部分学生无法形成完整的知识体系，导致学习效果不理想。因而，教材例题应该增加含总结环节的例题比重，以帮助学生更高效地学习知识，形成系统的数学知识结构。

2.增加开放型的数学例题含量

不同的问题类型侧重于培养学生不同的能力。封闭型问题的答案是确定的，能够帮助学生掌握数学解题的基本方法，体验数学知识的严谨性和科学性。而开放型问题的答案是多样的，在满足不同层次学生的学习需求的基础上，教师可以为学生制订个性化学习方案，提供发展自身个性和创造力的平台。北师大版教材中设置开放型问题的例题占全部例题的53.5%，而人教版教材中开放型问题占比只有21.2%，略显不足。

国际TIMSS、PISA等项目的测试题均设置了较大比例的问题开放型数学应用题，意图通过学生的表现揭示不同文化背景下学生发散性思维和应用能力的发展。朱德全等人也认为学生对开放性问题的解决能有效促进其实践性思维的发展。数学问题正如我们所处的客观世界，纷繁复杂，往往没有唯一确定的答案，结论开放的开放性问题，不仅能够使学生摆脱僵化的思维模式，更是实现分层教学目标的有利工具。[7]《义务教育数学课程标准(2022年版)》提出，数学课程要让学生“会用数学的眼光观察现实世界”“会用数学的思维思考现实世界”，教材中的开放型问题是学生运用数学眼光和思维联系现实世界的重要载体。因此，人教版的教材例题设计应该重视问题开放型的例题编排，将其作为教材个性化和数学开放性的重要体现。

3.加强例题与科学情境的联系

人教版和北师大版数学教材中设置科学情境的例题分别为12道和6道，占比分别为6.2%和1.7%。由此可以看出，两个版本的数学教材不够重视例题与科学情境的联系。这是当前教材编写中亟须关注和解决的问题。学科核心素养是当前教育研究高度关注的课题。2022年颁布的课程标准确立了以核心素养为导向的课程目标，提出了小学阶段的11个数学核心素养。多样化的情境是培养学生数学核心素养的重要基础。史宁中教授指出，只有在合适的情境中学生才能进一步感悟、理解、形成和发展核心素养。[8]国际PISA测试也是基于学生在不同现实情境中解决问题的表现进行素养评价，《PISA 2015评估和分析框架:科学、阅读、数学、金融知识和协作解决问题》(PISA2015AssessmentandAnalyticalFramework:Science,Reading,MathematicandFinancialLiteracy)将数学情境分为个人情境、社会情境、职业情境和科学情境。其中科学情境是指“与相对抽象的科学领域相关的情境，这种情境可能涉及某一个技术过程、理论或明确的数学问题的解释和理解”。我国《普通高中数学课程标准(2017年版)》提出，基于数学学科核心素养的教学活动应该创设合适的教学情境，数学情境应包含科学情境，具体指由离学生日常生活较遥远的科学实验、科学运动中可能面临的场景所构成的情境。

设置科学情境的例题，不仅能够增加例题情境的难度水平，锻炼学生解决复杂数学问题的能力，还能帮助学生拓宽视野，丰富其数学学习经验。因此，小学数学教材中例题的情境设置应当注重数学知识与科学情境的联系，丰富数学例题所关联的学科种类，如生物学、地理学、信息技术等，促进学生应用能力的发展。