干涉角度显微测量提高光子相关法空气声声压测量精度研究

杨荣岩， 赵 洁， 王大勇， 朱卫民

(1.北京工业大学 理学部 物理与光电学院，北京 100124；2.河南省计量科学研究院，河南 郑州 450047)

1 引 言

光学方法测量空气声声压是目前声学计量的研究热点。该方法具有非侵入性和高空间分辨率等优势，同时可以将声压通过激光波长溯源至SI单位，用于声压量值的扁平化传递。早在上世纪，Taylor首先提出了测量声波示踪粒子速度的概念，并在驻波管中成功测量出示踪粒子振动速度[1,2]；随后，Hann和Sharpe使用光子相关技术，通过分析光电探测器捕获的单个光子事件来解调声波示踪粒子速度[3～5]。

Koukoulas等进一步拓展了应用，使用光子相关法解调多普勒信号测量驻波管空气声声压，并将光学法与标准传声器测量结果之间的偏差降低到0.2 dB[6～11]。中国计量科学研究院在平面行波管内通过激光多普勒技术获得声场中示踪粒子的多普勒信号，使用频谱法分析得到不同频点的测量声压偏差与传声器所得的结果均低于0.3 dB[12,13]；该单位还使用光子相关法在行波管中解调多普勒信号得到粒子速度，测量出空气声声压，并分析了测量误差的主要来源[14,15]，将在驻波管中测量声压与实验室标准传声器测量结果的偏差降低至0.11 dB[16]。近来，韩国标准与科学研究院使用光子相关技术完成了自由场空气声声压的测量，并在0.5～16 kHz频率范围内，得到光子相关技术测量结果与传声器之间的差异在0.01～1.3 dB[17]。

上述光子相关法测量空气声声压系统中多采用双光束双散射光路，声压测量准确性受两光束夹角、光强差异、光束有效直径、干涉条纹间距、示踪粒子粒径等参数影响。为了让示踪粒子振动速度能够反映声场声压，实验中的声波示踪粒子要对声波有良好的跟随性,同时示踪粒子的直径和测量干涉条纹的间距必须匹配，一般来说粒径约为条纹间距的三分之二，以得到更高灵敏度和更宽的声压测量范围。两光束夹角影响干涉条纹间距大小，因此准确测量光束夹角对于光子相关技术准确测量声压装置和光路的设计有着重要意义。在实验的干涉区域内，干涉条纹的间距均匀性与光束质量、光束光强差异等因素有关，并随光束干涉位置和夹角变化，条纹间距的不均匀会导致多普勒信号频率的偏差和展宽，最终导致声压测量结果的误差，同时还要考虑干涉区内条纹间距不均匀性对夹角和间距推导关系的影响。

本文提出采用光学显微成像的方法将干涉条纹成像到CCD上，对条纹间距进行测量，并推导出干涉夹角。该方法测量干涉夹角误差小，提高了声压测量的精度。

本文还采用MATLAB仿真软件研究了干涉条纹间距均匀性与光束夹角、干涉光束交点位置等因素的关系，为光子相关法光路和实验装置的设计优化提供了理论依据。

2 原理与仿真

2.1 光子相关法测量空气声声压原理

光子相关法测量自由场空气声声压的原理示意图如图1所示。激光器射出1束高斯光束经过分束棱镜BS分成两束光强和偏振态相同的光束，分别经过平面镜M1和M2反射后，2束光在空间中相交而产生干涉区，在消声箱内加入少量示踪粒子(如图中红点所示)，示踪粒子于声场驱动下在垂直于干涉条纹的方向进行周期性振动时产生散射光信号，相对原始光信号产生多普勒频移，利用单光子计数器来捕捉单光子信号并解调出粒子运动的速度信息，进而推导计算出声场的声压。光路中使用透镜L1实现对散射光的会聚，从而提高测量灵敏度。

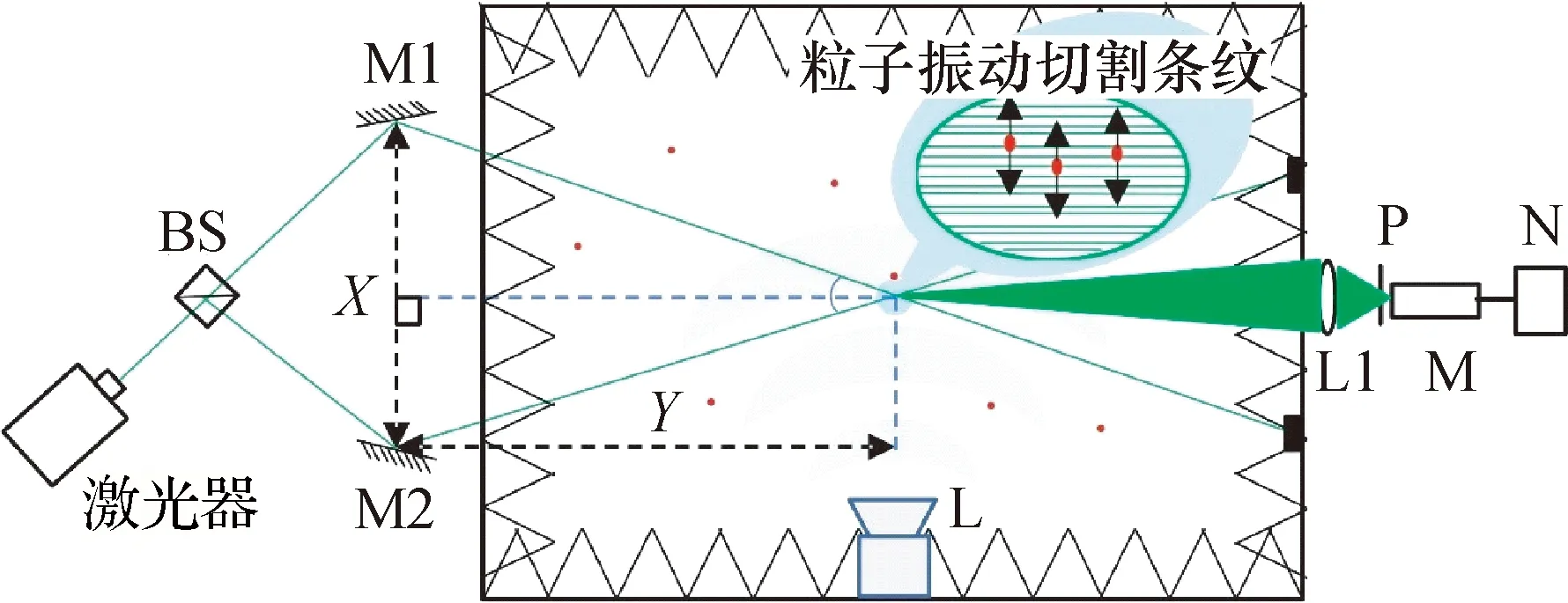
图1 光子相关法测量自由场空气声声压原理示意图

单光子计数器探测信号的自相关函数形式如下：

(1)

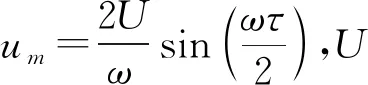
理论上干涉条纹间距为：

(2)

(3)

式中Tmin是自相关函数曲线到第1个极小值点的时间。

由声场粒子速度可以计算出声压为：

(4)

式中Z为空气特性阻抗。

从式(4)可以看出，在使用光子相关法测量空气声声压时，准确测量2光束的夹角和干涉条纹间距对于准确测量空气声声压是十分重要的。但是实验中干涉条纹间距和光束夹角并不是像式(2)所示的理想关系式，2束干涉激光光束均为高斯光束，2高斯光束干涉区的条纹间距与光束夹角、干涉位置和光强等因素有关。所以目前使用光子相关法测量自由场空气声声压时，将测量干涉条纹间距等同于测量光束夹角，这样处理会在实际测量中引入误差，因此实际实验中最好能做到直接观察干涉条纹并对其进行测量。

为了能够直接观察和测量干涉区条纹间距，减少目前测量光束夹角方法导致声压测量的误差，使用光学显微放大成像的方法采集两光束干涉区的条纹图像，测量出干涉条纹间距，再计算得到粒子振速和声压。在自由场空气声声压测量实验中，理论上干涉区的条纹间距通常小于2 μm，一般的CCD像元尺寸都大于这个数值，因此直接使用CCD不能观察到条纹。需要先使用显微物镜对干涉区的条纹进行预放大成像，然后就可以使用CCD直接拍摄到条纹图像，从而进行条纹间距的高精度测量和光束夹角的计算，最终获得更加精确的声压。

2.2 高斯光束干涉条纹随夹角变化的仿真分析

为了使用显微放大成像的方法测量光束夹角即干涉条纹间距，还需要考虑2束高斯光束整个干涉区中条纹间距的均匀情况，这对于测量结果有很大影响，因此使用MATLAB软件通过数值仿真考察高斯光束干涉区条纹间距均匀性，主要探究光束夹角和干涉位置对其干涉条纹间距的影响。

激光器发出的是高斯光束，具有一定的发散角，沿z方向传播的高斯光束在空气均匀介质中的复振幅表达形式为：

(5)

式中：E0为常数；ω0为束腰半径；ω(z)为光束半径；r2=x2+y2；k为波数；R(z)为曲率半径；η(z)为相位因子。

根据常用激光器参数，假定2光束在束腰处发生干涉，此时光束R(z)曲率半径为无限大，η(z)相位因子设为零，由光的干涉原理，得出2束高斯光束干涉区的光强分布为：

I=E×E*=|E|2=|E1+E2|2

(6)

假设激光波长为532 nm，高斯光束有效直径 为1.2 mm，两高斯光束夹角15°，通过仿真得到干涉区的干涉条纹，如图2所示。从图2中看出条纹间距分布均匀，看不到明显条纹畸变。

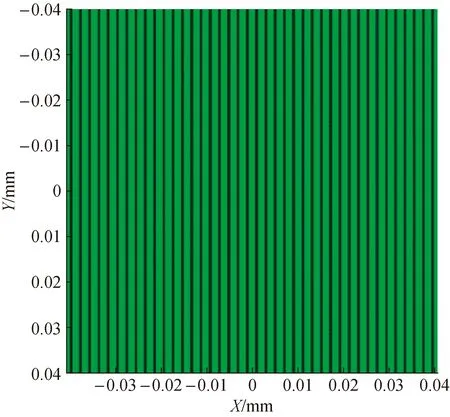
图2 高斯光束干涉条纹仿真图

通过改变仿真时两光束夹角，分别得出夹角较小和夹角较大时干涉区沿光传播方向不同位置处的干涉条纹间距，结果如图3(a)和图3(b)所示。

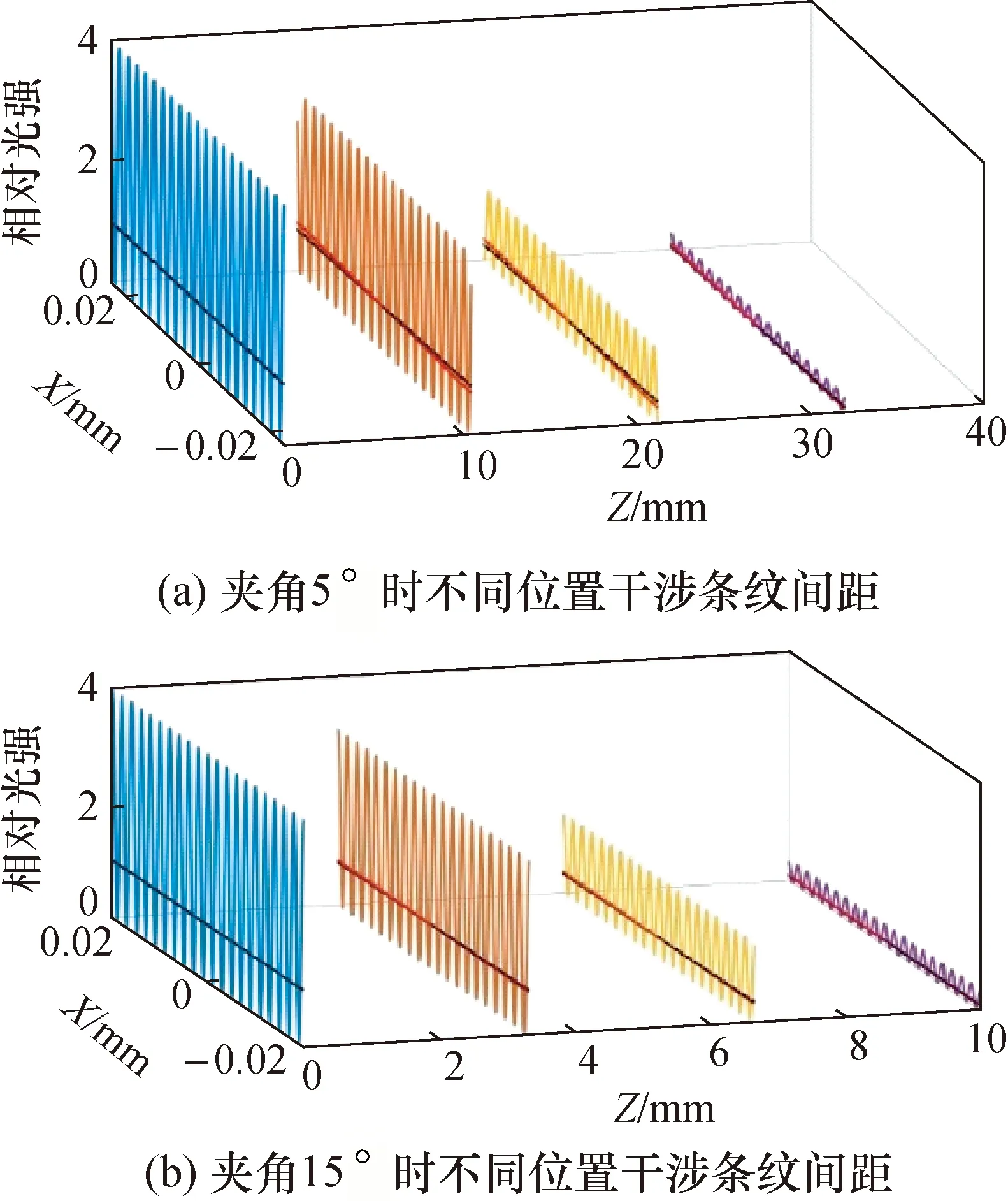
图3 不同夹角时的干涉区条纹间距

从仿真结果可以看出，当光束夹角为5°时，Z=0束腰处的干涉条纹间距为6.11 μm，Z=32 mm边缘处干涉间距为6.83 μm，边缘处干涉条纹间距明显增大；当光束夹角为15°时，Z=0束腰处的干涉条纹间距为2.04 μm，Z=10 mm边缘处干涉间距为2.07 μm，边缘处干涉条纹间距无明显变化。因此若严格在束腰处，两干涉光束夹角的变化对条纹畸变没有影响，对沿传播方向偏离束腰位置的区域，夹角对条纹畸变有影响。当夹角小时束腰处的干涉条纹间距不能代表整个干涉测量区的条纹间距，而2光束夹角大于15°时可认为干涉测量区条纹间距均匀，可以使用显微成像方法对条纹间距进行测量。

3 实验结果与分析

3.1 干涉角度的显微成像测量结果

实验装置包括：波长为532 nm、功率为300 mW的小型固体激光器，25倍显微物镜(NA=0.46)，像元尺寸为4.65 μm×4.65 μm、像素为1 280×1 024的CCD相机，USAF1951美国空军分辨率板，校准后的(型号)声级计。

显微成像方法测干涉角度的实验图如图4(a)所示，整个测量部分放置在消声箱内，实物图如图4(b)所示。

图4 显微成像方法测干涉夹角实验图

2束光强和偏振态相同的光在同一水平面上相交并形成椭球干涉条纹区，将显微物镜MO的工作端放置在光束交叉点处，在显微物镜的另一端放置CCD，此时通过调节CCD的位置以直接观察干涉条纹，CCD采集条纹结果如图5(a)所示，从图中可以看出椭球区干涉条纹间距均匀，可以进行后续的条纹间距测量。

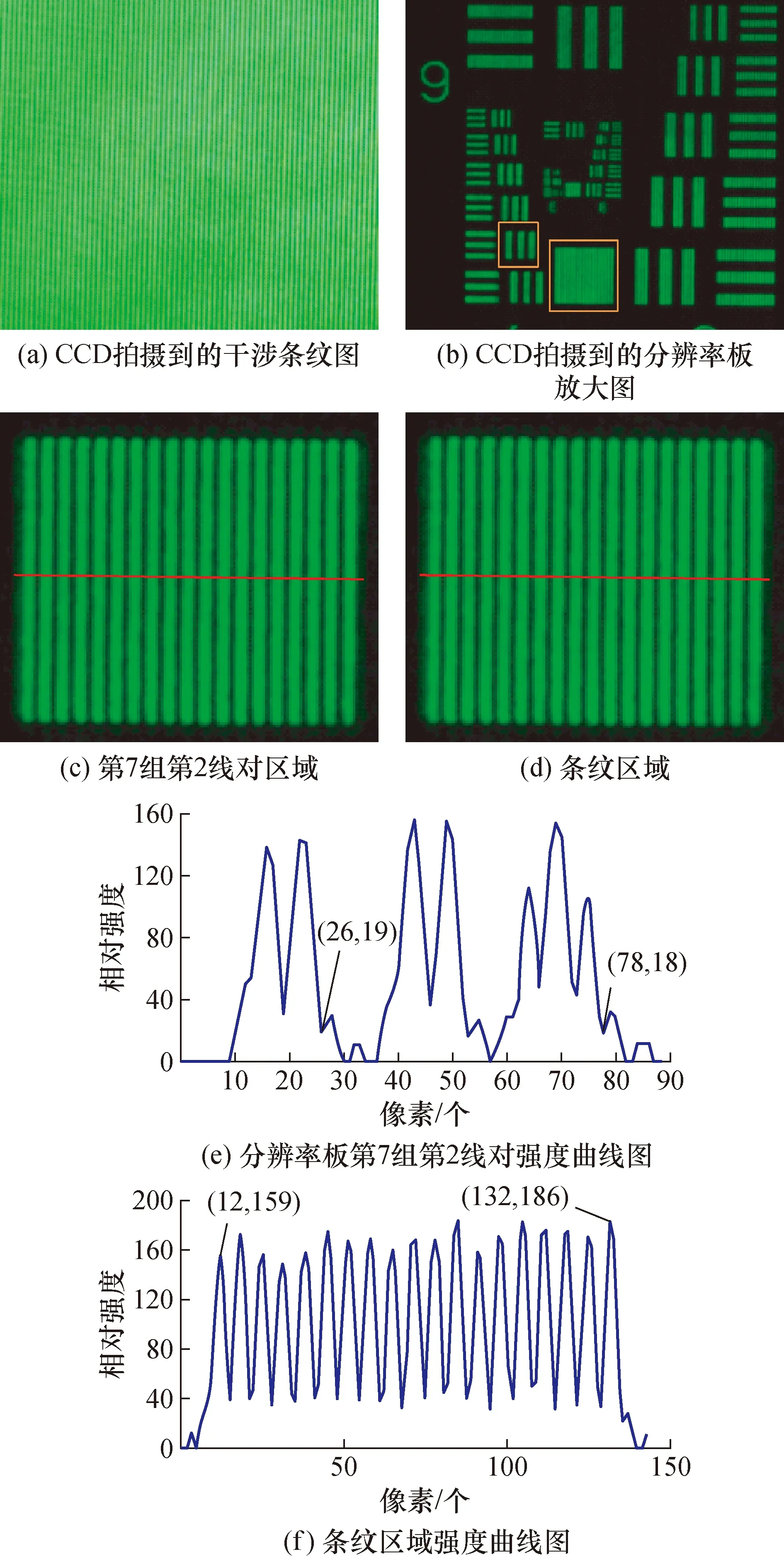
图5 实验数据处理

为了能够准确测量干涉区域实际条纹间距，在显微物镜的工作端加入透射型USAF美国空军分辨率板(由图4中R表示)。该分辨率板是由一系列周期不同的横向和竖向分布的靶条组成，作为标准物体，靶条的周期均为已知，其中外围尺寸大，越接近中心尺寸越小，有靶条处可以透光。在保证分辨率板处于干涉区内，固定分辨率板的位置，通过平移台移动CCD使其呈现分辨率板最清晰的倒立放大实像，拍摄到的结果如图5(b)所示，此时得到的显微像为分辨率板和同一位置的干涉条纹的叠加成像。首先，对显微成像的放大倍数进行标定，选择分辨率板的第7组第2线对作为研究对象，间距为1/144 mm。

图5(c)为拍摄图中所选标准线对的放大图像，作出图中红线部分光强与像素点的曲线，如图5(e)所示，每个像素大小对应于CCD的像元尺寸4.65 μm，从曲线中选取对应两边靶条相同右边界处两点，通过读出一个线对所占像素点数，可以得出该一个标准线对间距放大后的尺寸为120.9 μm，从而得到放大倍率为17.41。然后，采取类似的方式对干涉条纹周期进行计算，为了减少误差，尽可能选取包含多个周期的条纹，对应如图5(d)所示的条纹区域。对图5(d)中红线部分做出光强与像素点曲线，如图5(f)所示，图中每个峰谷分别代表条纹的亮暗，读出两峰值点之间的条纹周期数，以及总共占据的像素，得出每个亮暗条纹所占像素点数为6.7，从而计算出放大后的条纹间距为31 μm，结合标定的放大倍率，可以得到实际干涉条纹间距为1.781 μm。

在保证分辨率板在干涉区域的前提下，如图4所示中，多次改变分辨率板位置，相应的轴向移动CCD的位置进行调焦，在CCD上呈现分辨率板最清晰的像，拍摄多张分辨率板和干涉条纹的叠加放大图，按照以上步骤分别得到放大倍率和实际条纹间距。多次测量的结果如表1所示。

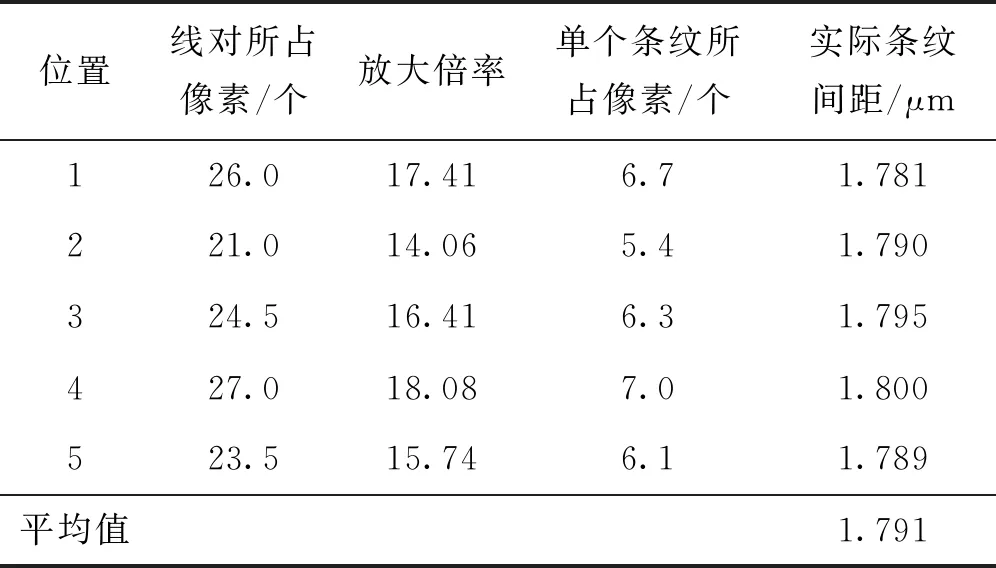
表1 不同放大倍率下得出的实际条纹间距

根据表中数据得出此时干涉区的条纹间距为1.791 μm，计算出两光束夹角为17.08°。

3.2 光子相关法测量空气声声压的结果与对比分析

根据自由场中光子相关法测量空气声声压的实验系统，分别使用本文提出的光学显微放大成像方法以及传统三角方法得出的条纹间距和光束夹角进行空气声声压测量，分别得出最后的声压级与标准声级计测出的声压级进行对比，以验证本文提出方法的可行性。

对于图1中的X和Y值使用米尺测量5次，并求出平均值，结果如表2所示，因此空间距离测量最终结果为X=350.12 mm，Y=1 324.06 mm。使用直角三角形勾股定理可以算出2束光夹角为15.05°，对应条纹间距为2.030 μm。

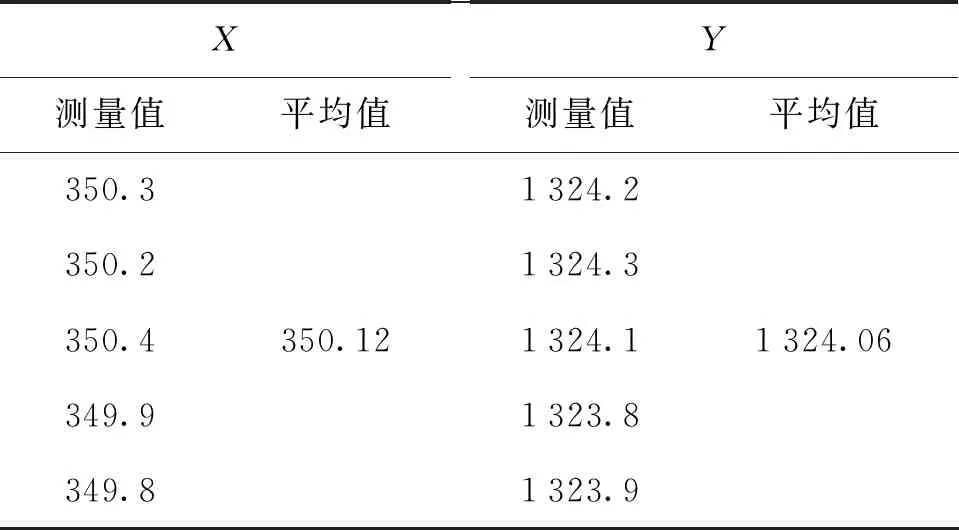
表2 多次空间距离测量结果

针对频率为1 000 Hz自由空气声场，在不同声压级的声场下分别取得自相关曲线和极小值时间，实验中得到的自相关函数曲线如图6所示，从曲线中读取到达第1个极小值点的时间Tmin。分别使用2种方法测出的条纹间距带入计算过程得出对应声压级，与标准声压级测量结果对比结果如表3所示。

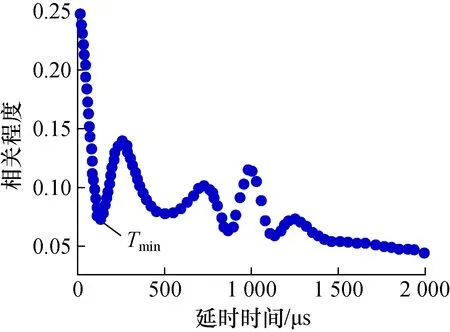
图6 光子相关法测量自由场空气声声压自相关函数曲线

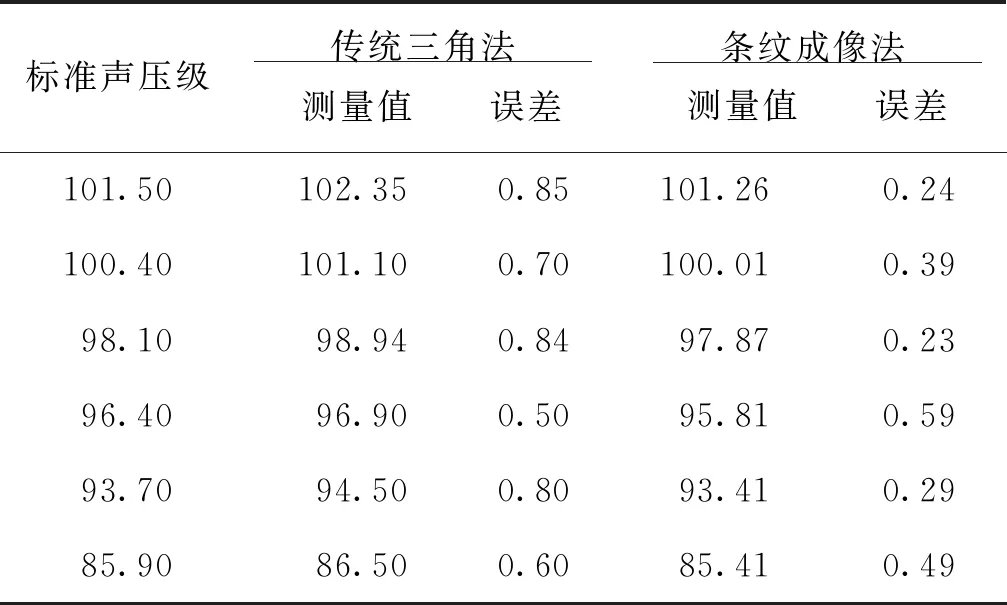
表3 两种方法得出声压级与标准声压级测量结果对比

标准声压级使用丹麦B&K公司2636测量放大器和4180传声器测量，仪器经中国计量科学研究院校准。

由结果可以看出，使用光学显微成像方法获得干涉条纹间距进行空气声声压测量的误差最大为0.59 dB，使用传统三角法测得的干涉条纹间距进行空气声声压测量误差最大为0.85 dB。说明本文提出方法获得的干涉条纹间距更接近于干涉区真实条纹间距，测量空气声声压结果误差更小，提高了测量结果准确度。

4 结 论

光子相关法测量自由场空气声声压过程中，需要准确测量干涉区域的条纹间距和光束夹角，本文提出采用光学显微成像的方法成功拍摄到干涉区条纹，通过标定出干涉条纹间距的放大倍率来求得干涉区实际条纹间距，推导出干涉角度。将该方法获得的干涉条纹间距和光束夹角应用于测量空气声声压中，复现出自由空气声场声压，与标准声级计测量结果误差为0.23～0.59 dB。与传统三角测量方法测得条纹间距和光束夹角用于自由场空气声声压测量得到的结果进行对比，表明本文提出的方法获得的干涉条纹间距和光束夹角更接近真实值，提高了自由场空气声声压复现精度。