直升机旋翼气动试验测力天平原位校准技术

汤 斌, 王文健

(北京长城计量测试技术研究所, 北京 100095)

1 引 言

直升机旋翼试验塔是旋翼试验过程中的关键测试设备,主要应用于旋翼启停特性、动力性能和飞行力学的试验验证工作,以保证旋翼系统的整体性能达到设计要求。旋翼试验过程中多维气动力的试验数据通过安装于旋翼试验塔顶部的多分量气动力测量天平(以下简称：旋翼天平)和扭矩传感器直接测得,其测量数据的准确性直接影响被测旋翼系统的性能评价结果。因此,旋翼天平在全寿命周期内需进行定期校准,以保证量值准确、数据可靠[1～3]。旋翼天平校准属于多分量力传感器校准领域,多分量力传感器目前广泛应用于工业制造和测试,尤其是航空航天领域如飞行器模型风洞试验、直升机旋翼气动力试验、发动机推力矢量测试等。文献[4]综述了多分量测力仪种类及其校准装置的研究现状,文献[5～11]介绍了风洞天平、天平的研制和校准应用案例,对于自身体积和吨位量程都较小的单体应变式或机械组合式多分量测力天平,在原位校准、在线校准技术等各方面研究工作均已较成熟和完善。旋翼天平属于大吨位复杂的机械式组合天平,直径最大近2 m,单分量力测量范围超过100 000 N,目前国内仍停留在直接拆卸系统中单个测力元件送认可机构实验室检定的方法。而旋翼天平内部结构复杂测力元件拆卸难度大,元件单独送检无法表征系统整体的测量特性。另据资料显示俄美等国家旋翼天平普遍采用原位校准方案。因此,我国在用的旋翼天平也需要研究原位校准技术,在其安装原位,模拟实际工况进行多分量气动力加载,实现系统级校准。

本文提出基于力叠加原理的组合加载原位校准方法,通过单分量高精度标准力输出装置对旋翼天平各分量测力方向施加校准载荷,加载架作为支撑结构保证标准力作用轴线与旋翼天平测力基准一致。标准力输出装置校准载荷与旋翼天平测量数据进行对比,实现旋翼天平的在线原位校准,确保旋翼试验过程中多维气动力测量的准确可靠。

2 旋翼天平原位校准方法研究

2.1 多分量旋翼天平工作原理

直升机旋翼试验塔作为直升机旋翼气动试验的大型非标专测设备,旋翼试验过程中除了旋翼旋转方向上的扭转力矩是通过传动轴上扭矩传感器测量之外,其它五维气动力均由试验塔顶部的五分量机械式旋翼天平直接测得,如图1所示。旋翼天平为浮框式机械天平,机械天平本身测量精度主要由标准传感器及定位安装精度保证。

图1 旋翼试验塔外形和测力元件

旋翼天平多维气动力测量的核心元件为正交测量轴系内对称分布的8只高精度大量程单分量测力传感器,其中4个测力元件垂直布置(S5、S6、S7、S8),用以测量旋翼试验过程中垂直方向上的力,另外4个测力元件水平布置(S1、S2、S3、S4),用以测量旋翼试验过程中水平方向上的力, 测力元件安装示意图如图2所示。全尺寸旋翼试验过程中,旋翼天平内部高精度单分量测力传感器输出对应测力方向上电信号经调理、放大、A/D转换后,由数据采集器采集并送至数据处理系统,数据处理系统再按照测力元件安装方向和位置确定的天平工作公式进行处理,得到旋翼试验过程中多分量气动力和气动力矩：升力(Fy)、阻力(Fx)、侧向力(Fz)、俯仰力矩(Mz)、滚转力矩(Mx);偏航力矩(MT) 由安装在传动轴上的扭矩传感器直接测得。

图2 旋翼天平工作原理

2.2 多分量旋翼天平原位校准方法

多分量旋翼天平原位校准方法的原理是：在旋翼天平实际安装原位,由标准力输出装置搭配加载架,通过特定的加载头,对旋翼试验桨毂连接端施加标准校准载荷,以标准校准载荷与旋翼天平数据处理系统解算的各个分量气动力数据作比较,实现对旋翼天平测量特性的计量保障,如图3所示。

图3 原位校准原理框图

旋翼天平的原位校准的关键是校准载荷的准确加载,天平安装在旋翼试验塔顶部,安装操作空间相对狭窄,校准载荷无法直接作用到旋翼桨毂连接端面上,因此相应的校准力和校准力矩须搭配特定的加载头或通过加载架转换受力轴线来实现。

如图4所示,根据旋翼天平现有结构特点,标准力输出装置沿旋翼天平测量坐标系轴线方向输出单方向标准力F,直接作用到旋翼桨毂连接端;力矩载荷方面,通过加载头几何尺寸及定位安装保证标准力F作用线与旋翼天平测量轴线平行距离l,以此间接获得标准力矩校准载荷M=F×l。

图4 标准力/力矩单点加载原理图

根据力的叠加原理,在正交轴系内平行或彼此正交的2个力可以相叠加,实现标准力的合成及多个分量方向的组合加载,如图5所示。2个标准力输出装置输出2个标准力F1、F2,作用在加载头对称方向上的两端, 当F1、F2同向相等时,合成标准升力Fy作用到桨毂受力端面上;当F1、F2同向不相等,则合成结果为升力Fy和滚转力矩Mx组合加载。

图5 标准力/力矩叠加加载原理图

3 旋翼天平原位校准装置结构设计

依据原位校准方法,设计特殊计量工装以及标准力输出装置等部件,以达到将输出校准载荷作用到旋翼天平测量轴系上的目的。原位校准装置主要包括标准力输出装置、加载架和加载头,其中标准力输出装置实现校准载荷的输出及末端测量、加载架为标准力输出装置提供可靠支撑的同时保证校准坐标系与旋翼天平测量坐标系基准统一、加载头实现校准载荷准确传递到旋翼天平测量端。标准力输出装置采用精密电动推缸方案,推力输出前端安装力传感器,测量加载过程中的实际校准载荷输出。相对于标准力输出装置,加载架和加载头的设计需要考虑旋翼天平结构特性,以实现可靠支撑和载荷传递。

侧向力和后向力可以通过单套标准力输出装置来实现,其实现的关键点在于,若采用标准力输出装置水平推拉施力,加载头需要有一个刚性较强、高度固定的支撑基础,而这在旋翼塔顶部空间实现非常困难。如图6所示,标准力输出装置仍固定在旋翼塔顶部基座上,采用绳索拉拽并通过定滑轮换向实现水平方向力的输出,同时拉力传感器布置在水平方向,避免滑轮摩擦力对标准载荷的影响。

扭转、俯仰和滚转等力矩的加载校准以及升力的加载校准,则需通过多个标准力组合输出的结构设计来实现。常规来说,升力需要设计支架垂直向上拉,但由于旋翼塔顶部空间及可行方案的局限,很难设计合适的支架支持,无法直接输出竖直向上的拉力。升力拟采用前文所述基于力叠加原理的组合加载结构,由2套标准力输出装置产生2个大小相同,方向相上的推力,如图7所示。

图7 升力加载结构三维建模

标准测力传感器通过定位法兰安装在横梁(升力加载头)上,通过机械加工精度来保证定位精度,确保标准升力的准确施加。俯仰、滚转力矩加载校准与升力加载结构类似,只是2套标准力输出装置1套产生推力,1套产生拉力。

扭转力矩加载同样采用绳索拉拽方式,如图8所示,2套标准力加载装置生根在旋翼天平顶部水平面上,采用滑轮机构进行加载力方向的直角变换,对扭矩加载头产生1组带力臂的侧向拉力。

图8 扭转力矩加载结构三维建模

扭转力矩加载结构的关键点在于,扭矩加载头上对绳索连接导向是圆弧形结构,可确保即使旋翼转轴法兰因受力发生位移或形变,其拉力加载方向也始终沿加载头圆弧的切线方向,这样即确保了力臂长度的恒定,2个方向的拉力抵消,只保留纯扭转力矩。

4 多轴自适应协同加载控制技术

校准控制系统的构成如图9所示,主控计算机通过PXI总线和CAN总线分别控制数据采集系统和加载控制系统,数据采集系统由力值传感器、电桥、数据采集设备和PXI总线构成;加载控制系统由步进电机和CAN总线构成。

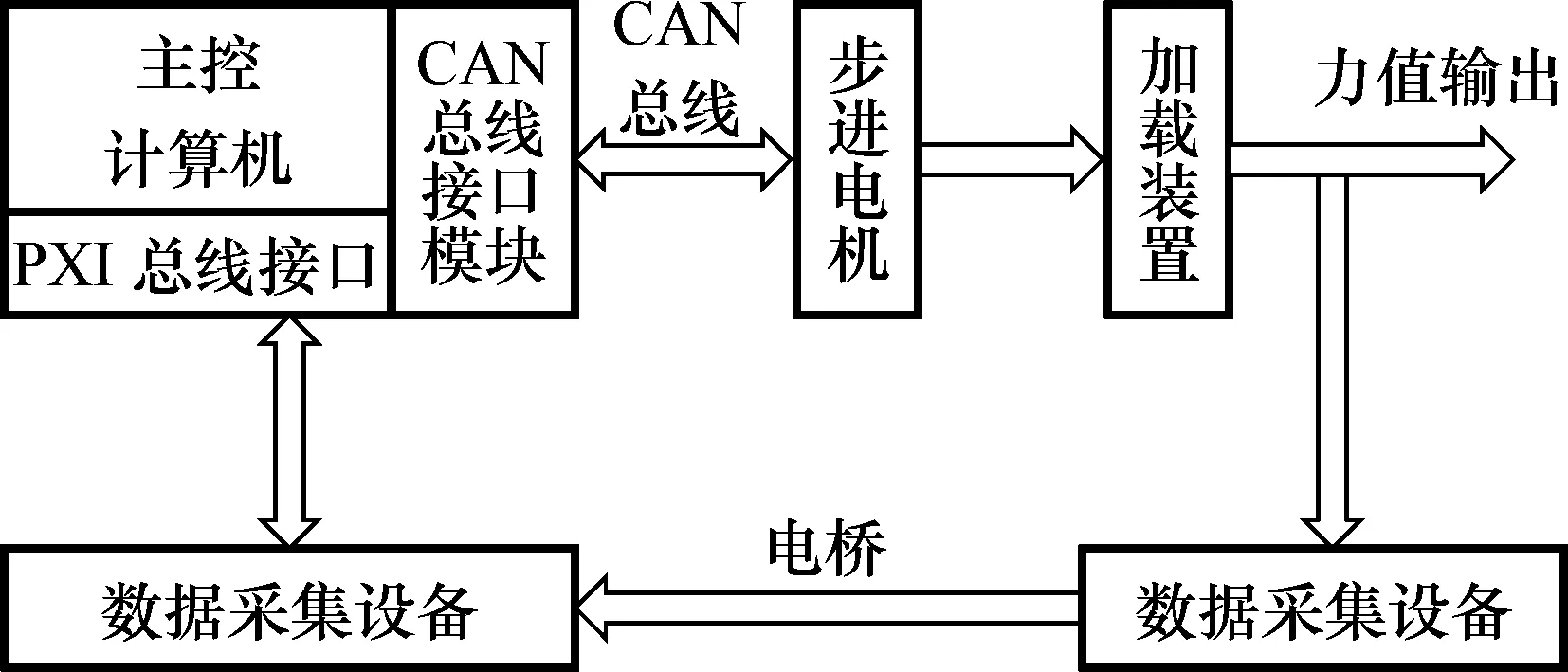
图9 控制系统数据采集系统结构图

由于受力结构的蠕变,加载点处的力值会缓慢降低,需要几十分钟或数小时才能达到稳定,因此设计了自适应协同加载控制系统,即以输入力值为目标,根据当前力值变化随时调节并稳定在设定的阀值内。经实验室台架试验验证,30 s内力值加载稳定性为±1 N。基于标准力/力矩叠加原理校准, 需采用多轴自适应协同加载控制技术,以克服2个轴输出力在加载过程中的相互影响,保证2套标准力输出装置同时精准的保持目标力值的输出。为此,设计了基于模糊PID的2电机协同控制算法,如图10所示,将一台电机视为主控电机,其它电机视为从动电机,主动电机的目标力值为操作员输入力值，而从动电机的目标力值由系统设定为当前主动电机对应反馈传感器的实测力值,模糊算法根据主、从电机轴实测加载力值之间的差值,实时修改从动电机PID算法的三参数,使从动电机可以实时地跟随主动电机运行,从而实现多台电机的协同加载,保证了2个标准力输出一致。

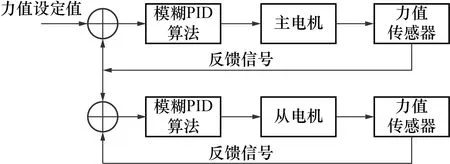
图10 多轴协同控制原理

基于多轴协同控制原理设计了算法程序,并进行实验室台架试验验证,2轴自适应协同加载控制系统30 s内的力值加载稳定性为±5 N。需要说明的是,协同控制的效果与被校系统的结构刚性、传感器受力应变量等直接相关,控制参数须在应用环境中反复调校。

5 高精度微小形变测量系统

旋翼天平原位加载校准过程中,加载结构受力后发生微小形变,加载头产生空间位移,使得施加的校准力存在误差,将直接影响旋翼天平原位校准精度。大吨位的力值/力矩加载,对机械加载结构是非常大的考验,机械加载结构的定型是建立在对加载头和支撑结构的受力有限元分析以及反复修改迭代的基础上,以达到加载点形变在mm量级范围内的目的,最终保障受力结构形变量达到校准误差允许的范围之内。为此研制了高精度微小形变测量系统,作为评估旋翼天平原位校准精度的关键手段。

采用激光三角法实现高精度形变测量,该方法结构简单,测试速度快,测量精度高,可快速得到加载点位移变化。设计立方靶块固定在承载横梁末端,传感器空间位置不变,旋翼天平原位校准过程中,立方靶块随加载点一同发生空间位移,立方靶块中心点变化可等效为加载点变化,如图11所示。由激光位移传感器测得立方靶块多点的空间变化,建立数学模型,可换算成靶块中心在竖直面内的绝对位移和角度变化[12]。

图11 微小形变测量系统结构

6 旋翼天平原位校准测试及数据处理

6.1 原位校准测试试验

根据大吨位旋翼试验塔测力天平结构耦合影响较小的特点以及旋翼天平的结构特性,采用各分量气动力依次单元校准,并结合多分量加载验证的校准方案。在旋翼试验塔现场,进行了原位校准试验测试,实验项目包括升力、阻力、侧向力、俯仰力矩、滚转力矩、偏航力矩6个分量气动力的单元校准。典型的升力单元加载及加载点形变测量结构如图12所示。

图12 升力单元加载时加载点形变测量

完成了水平面内阻力、侧向力的多分力组合加载校准和竖直面内升力、俯仰力矩、滚转力矩的多分力组合加载校准,多分力组合加载校准数据用来校验单元加载获得的原位校准公式,竖直面内多力素加载校验结构如图13所示。

图13 竖直面多力加载校准

需要说明的是,微小形变测量系统获得的试验数据显示加载点形变量非常小,经分析它对相对校准误差影响约为0.03%,证明了各加载结构刚性设计的非常合理,故将结构形变视为校准不确定度分量之一,不作校准力修正的处理。

对本次校准测试的不确定度进行了评估分析[13～14],考虑了综合加载重复性、载荷源(传感器)非线性及温度影响等误差、数采系统误差、机械结构加工和现场就位引起的综合加载误差、标准力输出装置的不稳定性等因素,综合评估得到旋翼天平各测量力素原位校准的相对不确定度均优于0.1% (k=2)。部分升力、侧向力、俯仰力矩、滚转力矩的单元校准试验数据见表1所示。

表1 单元校准原始数据

6.2 数据处理方法

旋翼天平原位校准试验的目的是在满足旋翼天平原位受载的前提下,尽可能模拟旋翼天平真实受力方向，施加校准载荷并求得天平各分量的输出值与所受载荷的关系。根据旋翼天平的特点,参照相关多分量传感器及应变天平校准规范[15～19],需要说明的是, JJF 20-2012《多分量测力仪校准规范》并未规定天平校准公式的具体型式,本文主要参照GJB 2244A-2011《风洞应变天平规范》和AIAA R-091-2003《风洞试验内式应变天平校准和使用》中的校准公式。由于旋翼天平为标准机械式天平,各测量方向线性较好,故天平校准公式采用一次多项式的形式：

(2)

截距项、主系数和干扰系数,分别为：

(3)

(4)

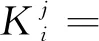
(5)

式中:k为加载点号;M为加载点数;Fs,ik为校准载荷;ΔNik为旋翼天平测量分量输出。

天平校准公式可写成矩阵的形式：

(6)

6.3 数据处理结果

根据第3.2节数据处理方法,应用MATLAB编写解算程序,求得旋翼天平校准系数矩阵。处理过程是：先导入原始数据直接进行最小二乘法线性拟合,可获得截距项和主系数,选取升力、俯仰力矩、滚转力矩、侧向力4个力的拟合结果如图14所示。

图14 线性拟合结果

耦合系数主要考虑垂直面内的升力﹑俯仰力矩﹑滚转力矩3个力素之间的耦合关系,可以获得交叉干扰系数,三者之间的耦合影响关系见图15～图17所示。

图15 Interference of lift force on rolling moment and pitching moment

图16 俯仰力矩对升力和滚转力矩的干扰

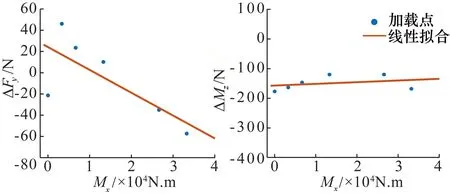
图17 滚转力矩对升力和俯仰力矩的干扰

解算截距项、主系数和干扰系数，最后获得的天平原位校准公式，与出厂校准公式比较见表2。

表2 原位校准公式和出厂校准公式比较

为了解力素之间的耦合关系对线性拟合精度的影响,分别统计了是否考虑耦合系数的不同情况,单元校准数据的拟合精度见表3所示。

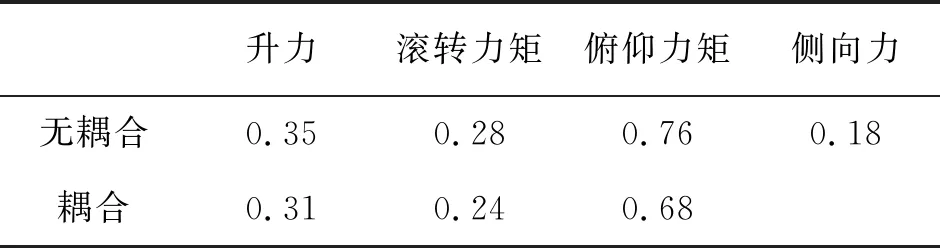
表3 相对拟合精度

利用天平原位校准公式,使用竖直面内多分力加载测试时的被测系统的原始数据进行校验,解算结果与此时的标准加载数据进行对比,获知升力﹑俯仰力矩﹑滚转力矩相对于校准载荷的最大相对偏差率为0.37%,和线性精度在一个量级,验证了原位校准公式是准确的。

从天平各分量的线性拟合精度可知,在考虑一阶交叉干扰系数的情况下,升力﹑滚转力矩﹑俯仰力矩的相对拟合精度提高的幅度有限(约为0.1%),各分量力的交叉干扰影响较小,说明该浮框式结构的组合式旋翼天平的内部解耦结构设计装调得非常好。

从校准公式(线性系数)可知,原位校准与出厂校准结果虽有偏差,但总体上比较接近,获得的各力素的线性系数相对偏差率为0.3%～0.8%。说明旋翼天平安装于结构系统中之后,测量性能不可避免地发生了变化,但整套系统稳定性和线性度依旧良好,可通过原位校准获得较准确的原位校准公式,提高旋翼气动试验测力系统的测力精度。

7 结 论

1) 基于力叠加原理的原位校准方法是可行的,可应用于大吨位旋翼天平校准,旋翼天平原位校准装置的研制工作,对其它类型多分量测力仪器的校准也具有一定的工程参考价值。推荐采用精密电动推缸作为的标准力输出源,它具有小型便携,加载精度高、响应快、易于自适应控制、易维护等优点;推荐组建具有自适应协同加载控制能力的自动化校准系统,它能有力保证原位校准的准确性,大大提高工作效率,特别是在多分力加载校准的组合方式非常多、校准载荷数据与被校系统数据量非常大的背景下,该装置准确高效的优点更为显著。

2) 提高校准不确定度的关键在于工作细节中精细把控。例如保证力加载点定位与力臂几何长度准确等相关的机械结构;力加载结构刚性的设计与验证方法;力值精确加载控制的算法程序等方面。

3) 原位校准可获得现场系统级校准的计量特性,这是实验室计量校准或拆卸测量元件单独校准所无法比拟的,从提高在用测量系统的实际使用性能角度来说,本文的实践工作具有较强的现实意义。

4) 本文在数据处理方法的讨论研究中,建立了只考虑一次主系数和一次干扰系数的简化的天平校准公式数学模型,数据拟合精度基本满足应用需求。是否可以适当考虑引入二次主系数以建立更合理的数学模型,或者考虑引入一元线性回归或者神经网络等拟合方法,来进一步提高拟合精度,是下一步值得深入研究的方向。