白木通4份种质叶片形态差异及叶面积反演模型研究*
2022-08-23许易梅刘红昌徐松陈伟宋章平
许易梅,刘红昌,2,徐松,陈伟,宋章平
(1.贵州大学 农学院,贵州 贵阳 550025;2.贵州省药用植物繁育与种植重点实验室,贵州 贵阳 550025;3.贵州省三滴水农业劳务服务有限责任公司, 贵州 贵阳 550309)
叶片是大部分植物进行光合作用的主要器官,其对资源的获取和利用的效率直接决定着植物生物量的大小[1]。叶片功能性状,如叶片大小、质量和年限,与植物生态策略和生态系统功能息息相关[2-4]。在叶片性状中,叶片的大小有着特殊的意义,叶面积(LA)可以反映叶片对光能的截获能力,一定程度上影响着植物的光合效率,同时,叶片大小与形状也是区分物种的重要指标。如西红柿(Solanumlycopersicum)坐果后较大的叶面积能增加成熟果实大小[5],这对于某些以果实大小、果肉硬度和甜度为重要果实品质性状的植物(如李属Prunus植物)非常重要[6];李属植物成熟果实大小主要取决于产量效率、叶面积和作物负荷之间的关系[4]。叶面积减少可能会出现更高的落果率,从而导致果实发育所需的可用资源减少[7]。因此,用模型快速准确地估计叶面积对果树叶面积的分析显得至关重要。叶面积测定常用方法有打孔法、方格法、称重法等,这些方法需要将叶片摘下,具有破坏性、费时费力且无法实现动态测定。叶面积仪虽然可以快速测定叶面积,但测量结果受拉出叶片的速度影响,人为误差较大[8]。在较大的物种群体中获得精确的叶面积,标准方法是基于图像识别软件扫描完整叶子的图像进行测量,但这通常需要花费大量的时间和人力,且仪器昂贵[7]。利用叶片叶形特征建立叶面积预估模型是常用手段,该方法对仪器的要求不高、成本低、简单易操作,是目前叶面积测量的理想方式[10-11],已成功运用于香樟(Cinnamomumcamphora)、西番莲(Passifloracaerulea)、香蕉(Musanana)、毛竹(Phyllostachysedulis)、玉米(Zeamays)、长白落叶松(Larixolgensis)和杉木(Cunninghamialanceolata)等植物的叶面积模型建立[12-18]。
白木通〔Akebiatrifoliata(Thunb.)Koidz.var.australis(Diels)Rehd.〕是木通科(Lardizabalaceae)木通属(Akebia)植物三叶木通(Akebiatrifoliata)的变种,其未成熟果实可作为中药材预知子入药[19],成熟果实(俗称“八月瓜”)果肉中富含氨基酸、维生素、葡萄糖、甘露糖等多种营养物质,具有果用开发价值[20]。四川省和贵州省分别于2018和2021年先后发布八月瓜食品安全地方标准,奠定八月瓜药食同源的基础。目前,白木通已在贵州、四川、江西等地陆续展开种植,但各区域种植的白木通种质混乱,叶片大小参差不齐。植物叶片的大小与水分和温度有关,大的叶片需要蒸腾更多水分来降低叶表温度,当水分不足时,植物会通过减小叶面积来减少水分消耗,同时避免高温灼伤[21]。通过研究白木通不同种质的叶片大小,或可在此基础上对白木通的光温习性和水分需求特性作出一些合理的假设,并促进进一步的研究。目前,关于白木通叶片生物学特性的研究主要集中在光合特性及矿质元素含量方面[22-24],暂无有关叶片形态的研究。白木通的叶片为复叶,具三小叶,该特殊的叶片结构为其叶面积的测量增加了工作强度。因此,为快速、准确地测定白木通的叶面积,本试验以贵州本地种植的4份白木通种质为研究对象,通过测定其叶形指标,建立叶面积反演模型,以期能减少大田工作中的人力物力投入,为其叶片的生物学特性研究提供参考。
1 材料与方法
1.1 试验地概况
试验地点位于贵州省开阳县南江乡新隆村干坝组(26°56′35″N、107°2′39″E),海拔1 100 m,采用平地种植,向阳通风。
1.2 供试材料
供试材料经贵州大学植物鉴定中心鉴定为木通科木通属植物白木通,采自开阳县本地野生白木通,共计4份种质,经开阳县御果种植园于2015年人工驯化而得。根据本课题组前期研究结果,筛选出各具优势的4份种质供试。BMTGKN-1(Q):果皮光滑,未成熟果实色泽绿色,成熟后为淡绿泛紫水晶色,具有感病少、成熟果实储存期长、果皮未开裂果实便成熟、耐运输的优势;BMTGKN-2(Z):果皮皱缩,未成熟果实色泽绿色,成熟后果实为苦瓜色,具有种子少、果肉可食率高、种子部分败育的特征;BMTGKN-3(ZI):果皮光滑,未成熟果实色泽绿色,成熟后为纯紫色,具有果实色泽鲜艳、果色均匀的特征,是目前市面上种植较多的白木通种质;BMTGKN-4(M):未成熟果实色泽绿色,成熟后为灰褐色。具有果皮薄的特征,是目前种植范围最广的白木通种质(图1)。
图1 白木通4份种质成熟果实颜色
1.3 测定指标及方法
待春季萌生的新叶生长定型10 d后,以随机取样的方法,每份种质随机选取9株植株(3株为1个重复),每株采集10片生长完好且无病虫危害叶片,置于冰盒带回实验室测定叶形指标,具体包括左小叶、顶叶、右小叶的叶柄长(PL,petiole length)、叶长(LL,leaf length)、叶宽(LW,leaf width)、叶面积(LA,leaf area)和复叶叶柄长等指标。其中,叶柄长、叶长和叶宽使用数显游标卡尺测定,叶面积采用叶面积仪LI-3100 AREA MATER测定。叶形指数(LI,leaf shape index)=叶长/叶宽。
1.4 数据处理
1.4.1 数据预处理
参照巫娟等[15]的方法,将各种质叶片所测得的原始数据按2︰1的比例随机分为建模集和测试集,每份种质建模集和测试集数据分别为60组和30组。其中,建模集用于叶面积模型的拟合,测试集用于模型验证。
1.4.2 叶面积模型的建立及评价
参照文献[13-18],分别以每份种质左(L)、顶(M)、右小叶(R)的LL、LW、LL×LL、LW×LW、LL×LW为自变量,各小叶叶面积为因变量进行回归分析,构建每类叶片的幂函数(F1)、抛物线函数(F2)、对数函数(F3)、线性函数(F4)和指数函数(F5)5种预估模型(图2)。同法构建4份种质的小叶和复叶综合模型,计算所有模型的决定系数(R2)、均方根误差(RMSE)和相对误差(RE),用以评价模型精度。评价标准为[25]:R2较大、RMSE和RE较小。
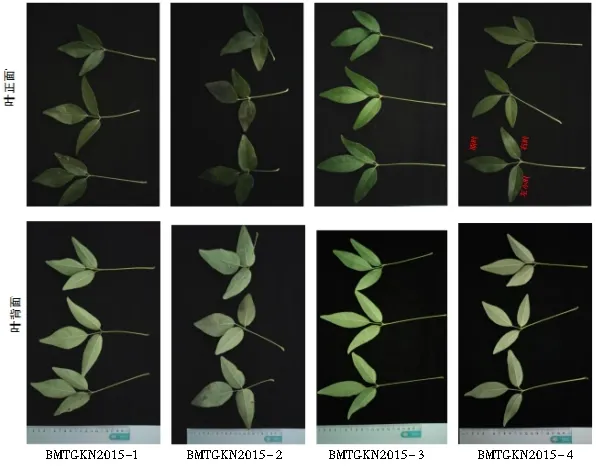
图2 白木通4份种质的叶片
数据统计、预处理使用Excel 2003,多重比较和热图制作使用SPSS 19.0。
2 结果与分析
2.1 不同种质叶形指标特征及稳定性比较
2.1.1 不同种质叶形指标的比较
所有小叶LW均呈ZI>M>Z>Q的规律,左、右小叶LI呈Q>M>ZI>Z的规律,顶叶LI呈M>Q>ZI>Z的规律;4份种质的顶叶各种叶形指标均大于左、右小叶,左、右小叶的叶形指标近似相等;除LW、LI外,不同种质叶形指标均呈ZI>M>Q>Z的规律(表1)。
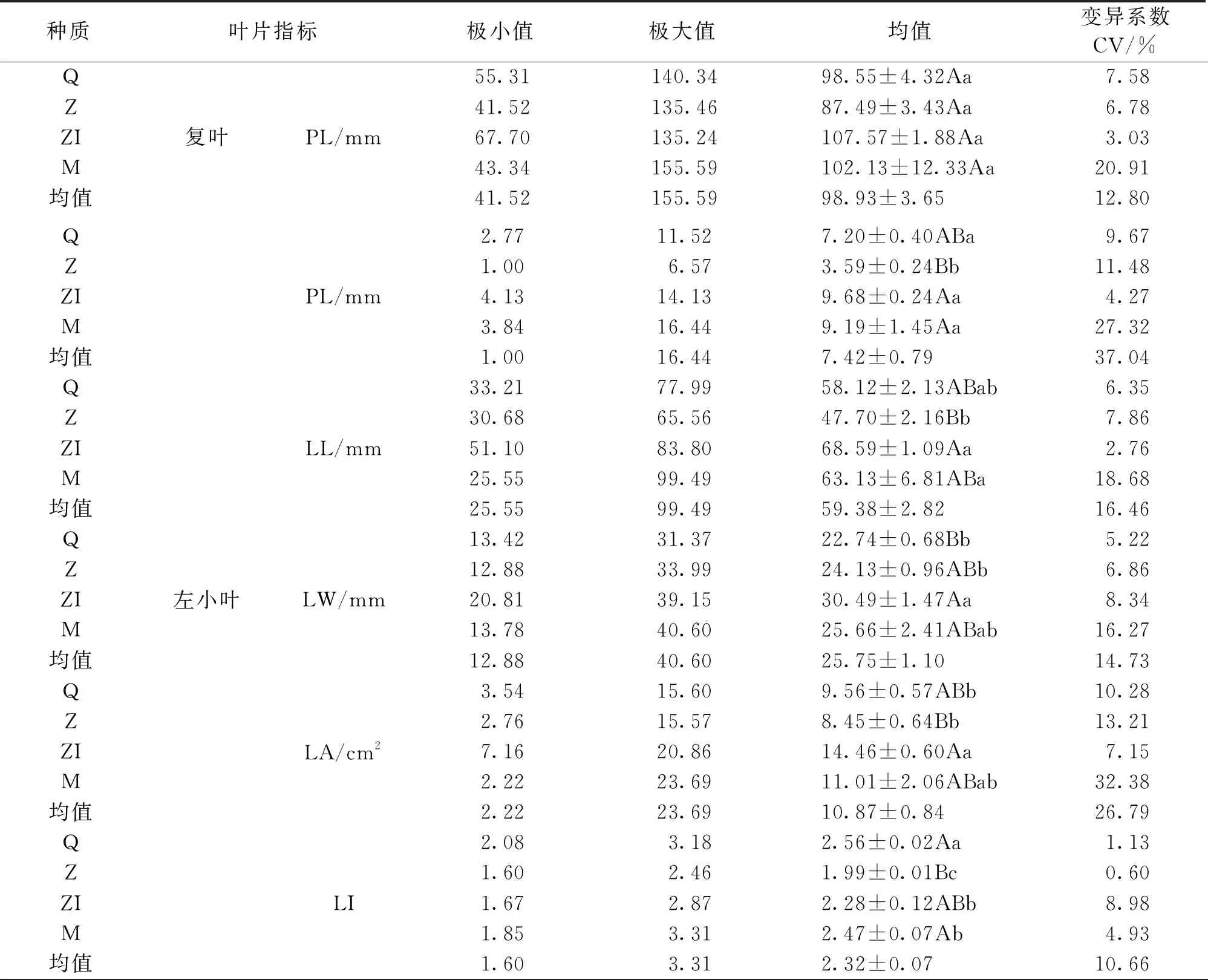
表1 白木通4份种质叶片叶形指标描述性统计及多重比较
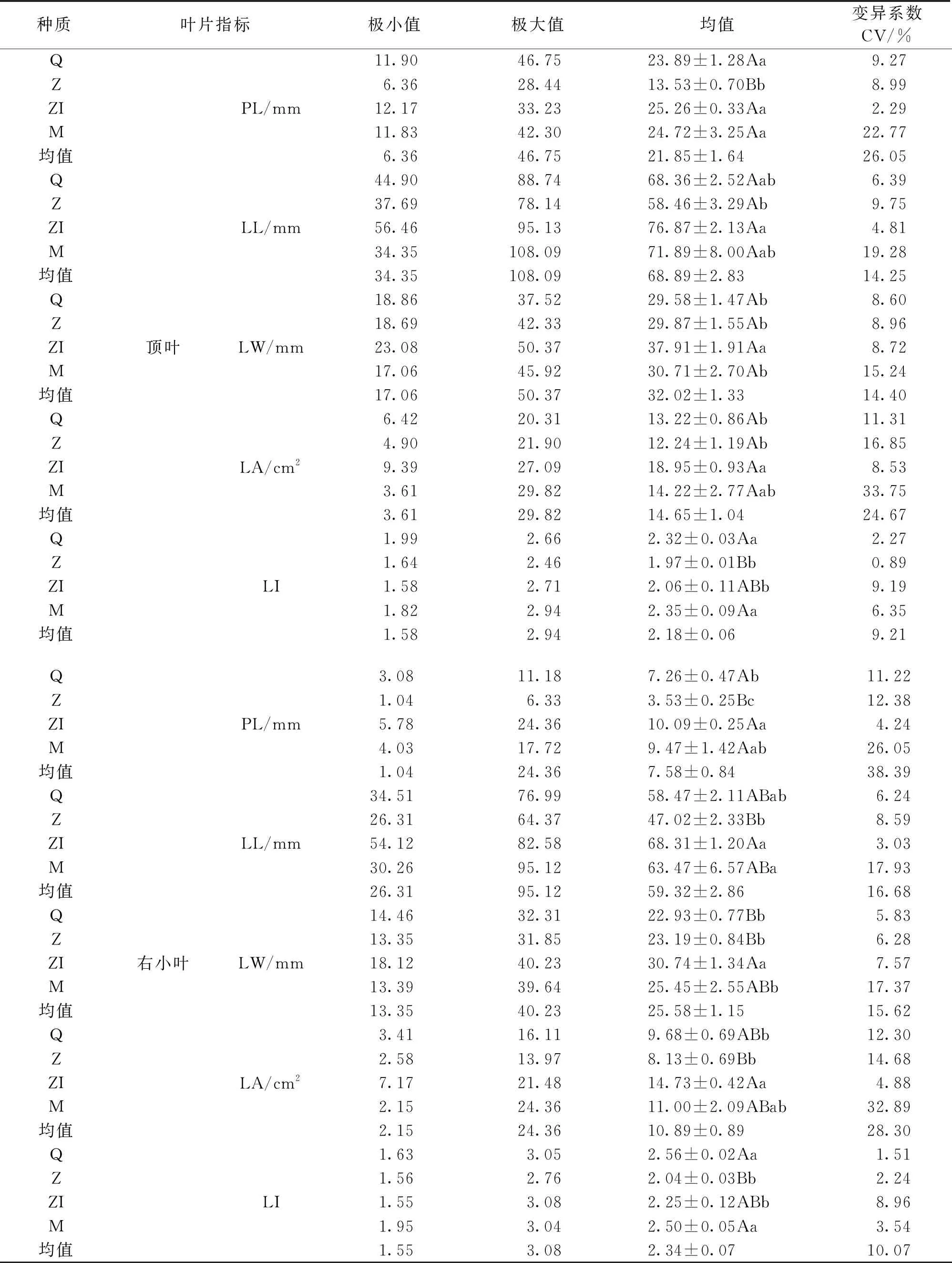
续表1
除复叶PL外,4份种质的其余叶形指标间均存在显著差异。其中,对于左小叶PL,Z与ZI、M差异极显著,与Q差异显著,ZI与M和Q间差异不显著;左小叶LL以Z最低,显著低于ZI和M,其余各种质间无显著差异;对于左小叶LW,ZI与Q差异极显著,与Z差异显著,其余种质间差异不显著;对于左小叶LI,Z极显著低于Q和M,显著低于ZI,Q显著大于ZI和M,ZI与M间差异不显著;对于左小叶LA,ZI极显著大于Z,显著大于Q,与M差异不显著(表1)。
Z顶叶PL最低,极显著低于ZI、M和Q,后三者间无显著差异;Z顶叶LL显著低于ZI,其余种质间无显著差异;ZI顶叶LW显著大于M、Z、Q,后三者间无显著差异;对于顶叶LI,Z极显著低于M和Q,ZI显著低于M和Q,其余种质间差异不显著;ZI顶叶LA显著大于Q和Z,其余种质间无显著差异(表1)。
对于右小叶PL,Z极显著小于其他3份种质,Q显著小于ZI,其余种质间无显著差异;Z右小叶LL极显著小于ZI,显著小于M,与Q差异不显著,其余种质两两间差异也不显著;ZI右小叶LW极显著大于Z和Q,显著大于M,其余种质间差异不显著;Q和M右小叶LI极显著大于Z,显著大于ZI,两者间差异不显著,ZI与Z差异也不显著;ZI右小叶LA极显著大于Z,显著大于Q,与M无显著差异,其余种质两两间无显著差异(表1)。
2.1.2 不同种质叶形指标稳定性
4份种质5类叶形指标的种间变异系数范围为9.21%~38.39%,LI的变异系数最小,左、顶、右小叶LI的变异系数分别为10.66%、9.21%、10.07%,变幅分别为1.60%~3.31%、1.58%~2.94%、1.55%~3.08%;小叶PL的变异系数最大,左、顶、右小叶PL的变异系数分别为37.04%、26.05%和38.39%,变幅分别为1.00~16.44 mm、6.36~46.75 mm、1.04~24.36 mm。主叶PL和小叶LI、LW、LL的变异系数较低(9.21%~16.68%),表明这4个性状变异幅度较小,遗传较稳定;小叶PL、LA变异系数较大(24.67%~38.39%),表明这2个指标变异较丰富,性状稳定性较差(表1)。
2.2 不同种质小叶叶面积预估模型的构建与评价
为比较叶形指标和函数模型对建模精度的影响,对评价模型精度的指标(R2、RMSE、RE)分别进行叶形指标和模型类型两个维度的方差分析,并使用LSD进行多重比较。根据R2最大、RMSE和RE最小的原则确定各种质各小叶建模效果较好的叶形指标和模型类别,为下一步的4份种质小叶和复叶综合模型的拟合提供依据。
2.2.1 叶形指标对叶面积预估模型的影响
图3为各叶形指标分别拟合不同小叶叶面积的模拟及验证精度统计量。基于R2、RMSE和RE值,对各小叶拟合效果最好的叶形指标为LL×LW(0.927≤R2≤0.972,0.542 cm2≤RMSE≤1.381 cm2,5.265%≤RE≤11.037%)。经验证,除M1外,其余小叶的预估模型精度均以LL×LW最高(0.756≤R2≤0.967,0.539 cm2≤RMSE≤1.604 cm2,5.805%≤RE≤12.707%)。虽然在M1的拟合模型中,以LL×LL测试集R2最大,RE最小,但RMSE却以LL×LW最小,综合建模集的表现,仍认为LL×LW对M1叶面积的拟合与预测效果较佳。因此,综合比较,对于4份种质的不同小叶而言,以各片小叶的LL×LW对小叶叶面积模型拟合效果和预测能力最好,建议选择LL×LW作为建立小叶和复叶叶面积预估模型的叶形指标。
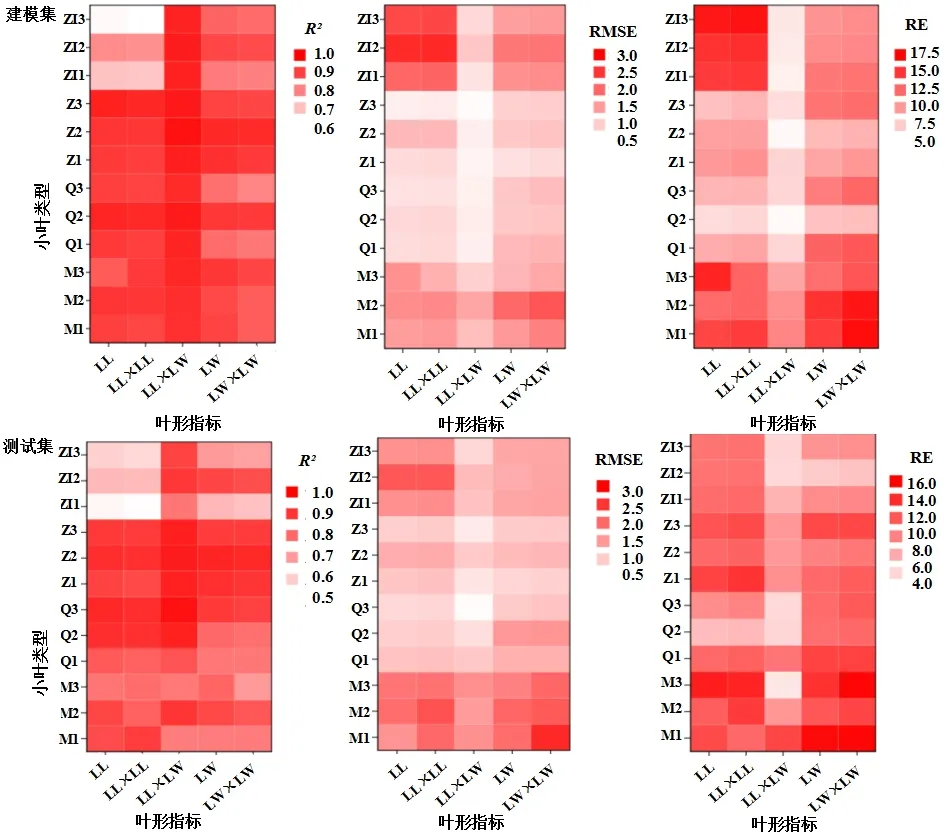
图3 不同叶形指标拟合模型的R2、RMSE、RE
2.2.2 回归方程对小叶叶面积预估模型的影响
不同模型对不同小叶的模型拟合和预测效果并不一致(图4),比较5类模型建模集的R2、RMSE和RE,F2对Q1、Q3、Z1、Z2、Z3、ZI1、ZI3和M2的叶面积拟合精度最高,F1对Q2、ZI2、M1和M3的拟合精度最高。经比较5类模型测试集的R2、RMSE和RE,F2对Q3、Z3、ZI1、ZI3和M2的叶面积预测精度最高,F1对Q1、Q2和Z1的叶面积预测精度最高,F4对Z2、M1和M3的叶面积预测精度最高,F3对ZI2和ZI3的叶面积预测精度最高。虽然Q1、Z3、ZI1、ZI2、M1和M3小叶叶面积拟合效果最佳的模型与预测效果最佳的模型并不一致,但两者之间R2、RMSE和RE均无显著差异。
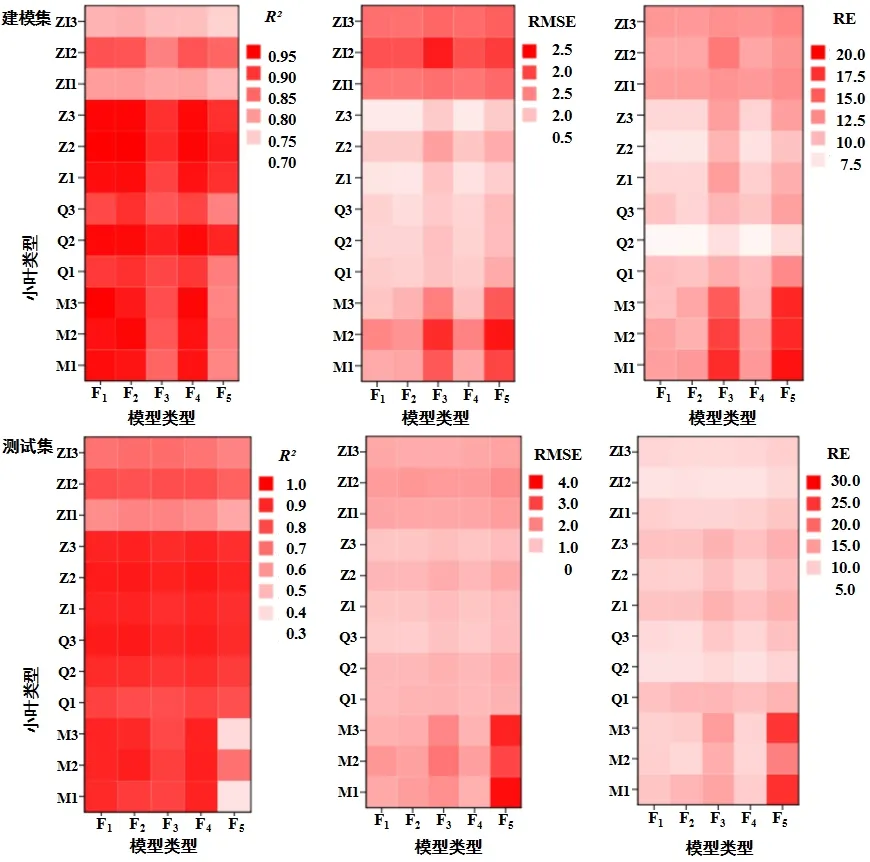
图4 模型类别对建模精度的影响
综合比较5种模型分别拟合不同小叶叶面积的建模集和测试集R2、RMSE和RE值,以F1、F2、F4对小叶叶面积的拟合和预测效果最好,建模集表现为:0.764≤R2≤0.950,0.666 cm2≤RMSE≤1.872 cm2,6.460%≤RE≤11.994%,测试集表现为:0.612≤R2≤0.936,0.778 cm2≤RMSE≤1.630 cm2,7.802%≤RE≤12.282%;F5对小叶叶面积的拟合和预测效果最次,建模集表现为:0.744≤R2≤0.922,0.890 cm2≤RMSE≤2.344 cm2,7.920%≤RE≤19.042%,测试集表现为:0.380≤R2≤0.904,1.034 cm2≤RMSE≤3.806 cm2,8.926%≤RE≤25.4%)。因此,建议选择F1、F2、F4建立小叶和复叶叶面积预估模型。
2.3 白木通4份种质小叶和复叶综合模型的构建
2.3.1 白木通4份种质小叶叶面积综合模型的构建及可靠度分析
根据前述分析结果,各种质3种小叶叶面积的预估模型均以LL×LW拟合模型最佳,但各小叶最适的拟合模型类型及预测模型并不一致,故在此基础上,以LL×LW为自变量,照前述叶面积模型构建方法,以总叶建模集的720组数据对所有小叶叶面积拟合F1、F2、F4三种预估模型,并以测试集的360组数据对模型可靠度进行验证,见表2。

表2 白木通小叶叶面积估算模型
F1、F2、F4三种模型均可以很好地估算各种质小叶叶面积,建模集R2在0.970~0.971,两两之间差值≤0.001,测试集R2在0.952~0.955,两两之间差值≤0.003,模型预测值与实测值之间的R2均达到了极显著水平。经比较模型精度统计量R2、RMSE和RE,建模集和测试集,均以F2:y=-0.001 8x2+0.702 1x+0.092 2的R2最大,RMSE和RE最小。其中建模集R2、RMSE和RE分别为0.971、0.885 cm2和7.184%,这说明以该模型拟合4份白木通种质所有小叶叶面积,拟合程度为97.1%,拟合效果较高,与实测值仅存在0.885 cm2的误差,偏差为7.184%。经测试集验证,该模型的R2、RMSE和RE分别为0.955、1.006 cm2和8.208%,这说明以该抛物线函数预测白木通4份种质的小叶叶面积,预测可靠程度为95.5%,预测可靠程度较高,与实测值仅存在1.006 cm2的误差,偏差仅为8.208%。F4:y=0.629 5x+0.711 5的建模集和测试集R2仅次于F2,分别为0.970、0.953,RMSE和RE均大于F2,建模集和测试集RMSE分别为0.868 cm2、1.030 cm2,RE分别为7.291%、8.403%。不论是建模集还是测试集,R2、RMSE和RE与抛物线函数绝对偏差均不到2.5%,这说明以线性函数拟合小叶叶面积拟合度和预测可靠度虽稍逊于抛物线函数,但也能取得不错效果。
2.3.2 白木通4份种质复叶叶面积综合预估模型的构建及可靠度分析
白木通叶由3片小叶组成,为更方便快捷测定其复叶叶面积,分别以左小叶(L-)、顶叶(M-)、右小叶(R-)的LL×LW为自变量,照前述小叶叶面积综合模型构建方法构建复叶叶面积综合预估模型(表3)。
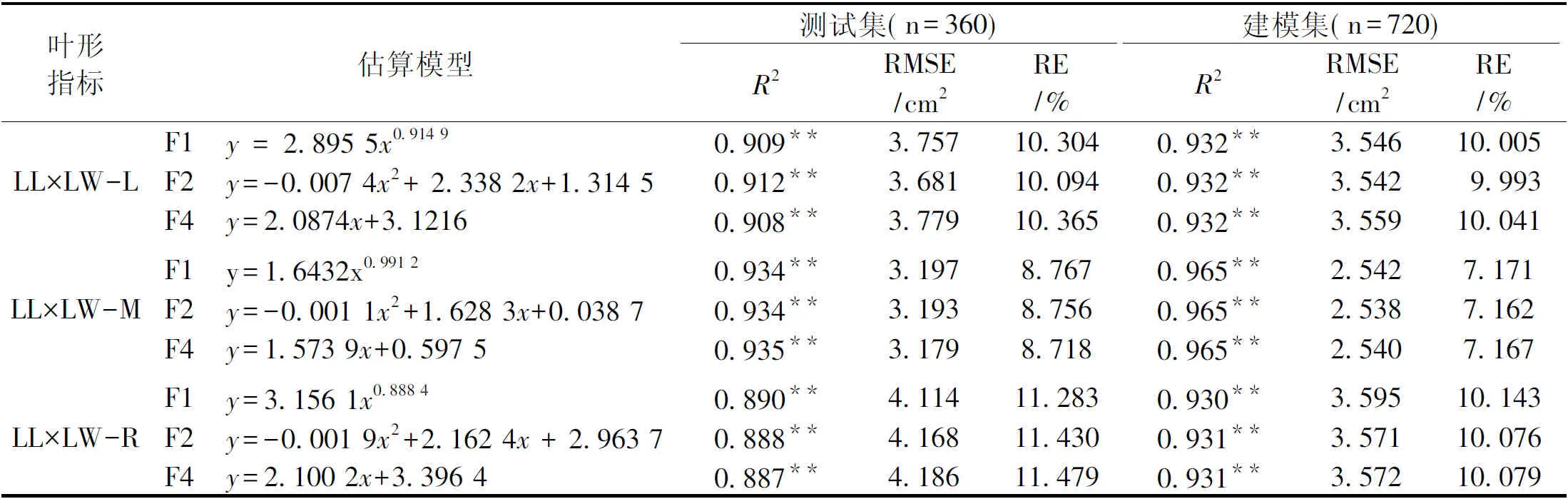
表3 复叶叶面积估算模型
经比较建模集和测试集R2、RMSE和RE,以M-LL×LW拟合的线性函数y=1.573 9x+0.597 5拟合效果最佳,相关指数达到0.965,RMSE为2.540 cm2,RE为7.167%。这表明以M-LL×LW对复叶叶面积实测值进行线性回归方程拟合,拟合度为96.5%,拟合度高,平均相对误差2.540 cm2,与实测值平均偏差7.167%。经测试集验证,该线性函数R2为0.935,RMSE为4.295 cm2,RE为11.779%,这表明以M-LL×LW为自变量,该线性函数对复叶叶面积预测可靠程度可达93.5%,相对误差4.295 cm2,与实测值偏差约11.779%。
3 讨论与结论
3.1 讨论
前人研究表明,比起使用LL或LW对叶面积进行单一纬度的函数模型拟合,二者乘积(LL×LW)对叶面积的预估效果更佳,该乘积乘以一个矫正系数(CF)能稳健估计叶面积,其中校正因子的大小取决于叶形[26-27]。Cain等[28]通过对18种不同叶形的植物矫正系数进行计算,其值在0.61~0.78,其中以LL×LW乘以矫正系数(2/3)能稳健估计巴西雨林卵形叶叶面积。Schrader Julia等[29]收集全球144科780种和亚种的植物叶片叶形指标,根据叶形的不同,矫正系数从高度分裂的裂叶到卵形叶的变化范围为0.39~0.70,这与本研究中白木通叶片(近卵形叶)叶面积线性模型系数在0.590~0.708的研究结果基本一致。
欧阳浩楠等[30]曾尝试以三叶木通小叶叶片LL、LW、以及LL×LW拟合同一生境内4种三叶木通的小叶叶面积,得出以小叶长宽的乘积对于叶面积进行拟合的效果最佳,这与本研究中得到的结果一致,但其所拟合的最优模型为线性函数,与本文的研究结果有一定出入。这可能是因为他仅对叶形指标做线性函数和幂函数的模型拟合,建模类型较少,所得最优模型因模型类别的限制可能并不是最优的,并且其未对模型精度进行校验,故与本文中得出的结果出现偏差;也可能是因为白木通为三叶木通变种,在叶片性状上两者间本身存在差异所导致的。
3.2 结论
生产上种植的白木通种质较杂,变异较大,本研究的4份白木通种质间叶片叶形指标均具有不同程度的差异,根据各种质叶形指标的差异程度,种质ZI和M应为长叶柄大叶型白木通,Q和Z为短叶柄中叶型白木通。通过叶面积反演模型的建立及验证,本文得出LL×LW是预测白木通小叶及复叶的较适叶形指标,其所拟合的抛物线函数模型(F2)和线性函数模型(F4)均能很好地预估白木通小叶叶面积,线性函数模型(F4)能很好地预估复叶叶面积,结果可靠程度较高。由于叶片的大小和形状因气候和生物地理区域而异[21,31],本次分析的结果仅能代表贵州省开阳县所种植白木通春季萌发新叶的叶形性状。在进行田间采样时,发现白木通不同生育时期萌发的叶片大小具有肉眼可见的差异,因此本文所得叶面积预估模型仅适用于该地区白木通叶片叶面积预估,该模型对于夏梢和秋梢萌出叶片以及其它生境的白木通叶片叶面积测定是否适用还需进一步研究验证。
