红壳竹与美竹的空间竞争关系研究*
2022-08-23郑轶文戴长志苏小飞张鑫周默言时培建
郑轶文,戴长志,苏小飞,张鑫,周默言,时培建
(南京林业大学 理学院 竹类研究所,江苏 南京 210037)
生态位是群落生态学中解释植物种间竞争与共存的一个重要概念。简言之,生态位就是生物生存环境的各个维度聚合体,具有相同或者相似生态位的物种聚集在同一区域,因为生态位的重叠往往会出现激烈的种间竞争。如果空间相对封闭,往往出现一方最终排挤掉另一方的竞争结果,如果生境中空白区域较多,则被排挤方可以通过提高扩散和繁殖能力,较快占据空白生境,等待外界干扰的发生(例如人为疏伐、火灾等导致的空白斑块),再占据被排挤方原先占领的生境斑块,实现物种间的动态共存,已有研究表明植物生态位分化可以缓解物种对资源竞争的激烈程度[1]。而植物生态位的分化表现在空间分布的不同(如空间隔离)和活动时间上的分化(如开花时间的差异)[2]。种群的空间分布格局是指同种生物在一定时空范围内的分布方式与配置特点,是种群内个体间、种群与所属群落异种个体间及种群与环境间相互作用的综合体现[3-4]。研究2个物种间的空间分布格局可以有效分析不同种群间的生存与竞争机制。目前存在着许多研究种群空间分布的分析方法,如:Ripley[5]提出的K函数、Diggle和Chetwynd[6]提出了空间聚集性的二阶分析法以及Baddeley等[7]提出异质性环境中的K函数。虽然这些分析方法很大程度完善与扩展了空间点格局的分析模型,但是也有局限性,例如2个或多个物种空间交互影响的分析不足,对时间尺度的分析欠缺。本研究介绍并应用特定类型概率的核估计方法用以检验分布于同一区域的不同类型点事件是否存在空间隔离,并分析时间尺度上的种群动态变化,完善种群生态位分化分析方法。
红壳竹(Phyllostachysiridescens)是一种适应能力很强,对土壤要求不高且不需要特殊栽培管理措施的优良竹种,具有竹笋食用、绿化观赏和竹材加工等多种用途[9]。美竹(P.mannii)是上等的农具用竹和篾用竹,具有竹材坚韧、篾性好、经久不裂的特性,其笋可供食用[9]。二者同属刚竹属(Phyllostachys)植物,成竹形态结构非常相似,为我国南方广布的竹种,然而对其空间分布规律和种间竞争机制的研究较少。经典生态学教科书上物种竞争都是以2个物种为素材进行,例如2物种的Lotka-Volterra模型,但是2物种竞争的实例并不多见,很多物种间的竞争的研究都是放在群落层面上对少数优势物种种间关系进行的,也有使用盆栽试验进行的。而本研究利用南京林业大学本部一个斑块环境中2种刚竹属植物的竞争作为素材,具有较好的代表性,这两种植物所处的环境处于封闭状态,三面都是水泥地面,另一面被水泥板隔断了鞭根的扩散,而样地内仅有一株小型木本植物,那么在这个相对封闭的环境中两种竹类植物势必存在激烈的竞争。本文研究红壳竹与美竹的空间分布状况,以及其空间结构随时间的变化,讨论二者之间竞争机制,可以丰富物种竞争理论,同时展示基于非参数核估计的空间分离方法在研究植物空间竞争的适用性,还可以检验在短时间尺度内竞争能力相对较弱物种通过空间分离可以实现和强物种的共存的假设,具有重要的理论价值。此外,本研究的结果对于合理规划不同竹种的种植区域具有一定的参考价值。例如,为快速实现竹类植物占领裸地(为控制绿化成本预留空白区域),可以通过引入强竞争植物加速弱竞争植物扩展到空白生境(即裸地),减少过密的种植密度导致的绿化成本上升问题。
1 材料与方法
1.1 研究区概况
研究区位于南京林业大学校园内(118°48′39.315″E、32°05′05.571″N),样地东南北三面均为水泥路面,西面为草坪,但为了防止竹林向草坪扩鞭,这一面地下埋了水泥板(图1)。

图1 红壳竹与美竹的空间分布
样地内红壳竹与美竹早先属于人为引种,经过多年生长,竹笋自发扩散,现有的时空分布基本反应了2种竹类在自然生长过程中相互竞争的结果。调查数据基本涵盖整个样地内红壳竹与美竹的发笋位置,该区域西边在2014年为防止竹笋扩鞭到草坪,使用水泥板隔断竹鞭向西扩散的可能,而该区域其余三面都是水泥地面,研究区域处于封闭状态(尽管理论上竹子鞭根可以沿着东北南三方地下扩张,但因为水泥地面和钢筋混凝土建筑的阻碍,鞭根无法产生钻出地面的竹笋)。2015年3月下旬开始发笋,3月31日进行第一次记录,以后间隔7 d记录1次,到4月21日2种竹子发笋基本结束。图1样方总共记录332个竹笋位置,其中红壳竹235个,美竹97个。
1.2 研究方法
1.2.1 特定类型的核估计
根据Diggle等[8]提出的估计和检验空间隔离的方法,假设数据是一个多类型、空间异质性的泊松点过程的实现(realization)。泊松过程模型的关键假设是不同类型事件相互独立。假设模型的每个过程都对应于一个特定类型的事件,并且是独立的泊松过程。则已知竹笋个体生长在位置x处(一个包含横纵坐标的二维向量),在这个条件下个体为k类型种群的概率可表示为:
这种条件概率被称为特定类型的概率。其中:k表示种群的类型(k=1,2,…,m),m为种群数量;λk(x)表示在位置x处第k个类型事件的强度函数,λk(x)=λ0(x)ρk(x),λ0(x)表示各事件类型(单变量)泊松过程的强度函数,ρk(x)表示在考察时间段内地点x处产生k类型种群的概率。对于空间结构函数ρ(·),如果ρk(x)=αkρ(x),αk为一个常数,那么称完全空间不分离;如果研究区域内只产生了一种类型的事件,即对研究区域内任意位置x的特定事件类型k,pk(x)=1,而对于其余类型事件,其特定类型事件概率为0,那么称这些类型事件在x处发生在空间上的完全分离。在实践中,使用以下方程对pk(x)进行估计。


图2 使用交互验证的极大似然估计来确定核估计的最佳带宽


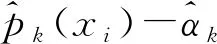
1.2.2 种群交互作用的K函数[11]
本研究使用一种多个种群空间关系的判别方法,这种方法建立在Ripley提出的K函数的基础上。K函数是解释种群空间分布关系的一种方法,简单来说,就是考量研究区内以某点为圆心,以一定长度r(即人为定义的距离尺度)为半径的圆内的植物个体数目的函数。而对2个种群交互影响程度的判别,以第1个种群的某点为圆心,统计一定长度r为半径的圆内的第2个种群个体落在此圆中的数目。此条件下交互类型的K函数。
式中:1和2分别表示两组点事件类型(竹笋在平面坐标系下的坐标被定义为点事件),即美竹笋和红壳竹笋;n12表示距离第1组任意点事件长度小于或等于r所有第2组点事件的数量;λ2表示单位面积上类型2点事件的平均数量;E表示期望值;r为距离尺度。
为了更直观分析两种点事件的空间关系,同时也为了使不同距离尺度下方差稳定化、减少方差非齐性的发生,通常用L函数代替:
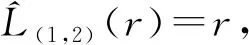
1.2.3 发笋数量随时间的增长函数
使用幂函数[12]和beta sigmoid函数(BSF)[13]来拟合红壳竹和美竹在不同调查时间出笋数量。
N=atb
式中:a,b,ropt,topt和tmax均为待拟合参数,t为时间(自变量),N为出笋数量(因变量)。分别使用这2个函数去拟合红壳竹、美竹的出笋数量,因为2个函数的参数数量不同,根据Akaike信息准则(AIC)去判断每个竹种适用的函数,因为AIC在非线性函数的拟合优度和函数的复杂性程度之间实现了权衡,经常被用于比较模型的优劣[14]。在2个模型中选择AIC最小的那个模型。
1.3 数据处理
利用统计软件R(版本4.2.0)[15]数据分析和作图,其中空间点格局和空间分离分析使用spatstat.core(版本2.4-2),非线性回归使用了IPEC(版本1.0.3)软件包,这些软件包都是R的特种软件包,需要在CRAN(https://www.r-project.org/)上下载。
2 结果与分析
2.1 红壳竹与美竹的空间分布关系
图3A和3B显示在研究样地中红壳竹与美竹的特定类型概率。可以直观地看出不同的竹种在不同的特定子区域占主导地位。越亮的区域发生其特定类型概率越大,即发生这种笋的概率越大。2种竹子发笋的空间分布有部分重叠,但两者直观上看有明显的空间隔离,红壳竹所占有的区域更大。随着植物的竞争与扩散,特定类型概率高的竞争压力越小,而特定类型概率低的更有可能与另一种竹子混交,竞争压力更大。基于399次蒙特-卡罗模拟检验,得到的P值等于0.002 5(<0.05),表明红壳竹和美竹存在空间生态位分化。
图3C和3D是红壳竹和美竹基于蒙特-卡罗模拟得到的风险趋势面。图中越亮的区域代表其P值越低。图中0.025的P值等值线围成的区域否定原假设,即此区域发生某种类型竹笋较另外一种类型竹笋概率更高。

图3 红壳竹(A与C)和美竹(B与D)特定类型概率的核估计与风险趋势面
图4是2个竹种的空间分布值L(1,2)(r)-r估计值图像,1、2分别代表红壳竹和美竹,反映了给定尺度下,二者交互影响程度。从图4看出,在0.2~2.5 m的尺度下,红壳竹与美竹观测组L(1,2)(r)-r估计值完全在上下包迹线之下,说明2竹种发笋存在空间上的排斥关系,也验证2种竹子的空间分布隔离效应。而0.2 m距离尺度以下,两者相互独立,但此距离已经非常小,可能只是反映了单个竹笋的空间占据的最小范围。

图4 红壳竹和美竹空间关系的检验
2.2 发笋量时间尺度上的变化
不同种类竹子发笋的数量随时间的变化不一样,一般而言,在一个群落中,竞争能力较强的种类发笋的量大且随时间变化增加的多,反之,则发笋量小且随时间变化增加的少。因此,评价物种在群落中的竞争力,新个体的扩散快慢很重要。在本试验中,依据出笋的数量(N)与间隔时间(t)的数据进行不同函数模型分析,拟合结果见表1。基于AIC的比较,红壳竹的出笋量随时间变化更符合幂函数,而美竹更符合限制性的sigmoid函数。强制性使用sigmoid函数去拟合红壳竹的累计出笋数据,虽然可以得到低的残差平方和(RSS),但是参数的估计值明显与实际相违背,因为beta sigmoid函数(BSF)中的topt和tmax分别代表出笋速率达到最大的时间和出笋结束的时间。与之不同的是,美竹数据拟合得到的BSF的参数较为合理。图5给出2个竹种选用不同方程得到的函数图像。从函数曲线可以看出红壳竹的出笋速率远高于美竹的出笋速率,说明红壳竹的竞争能力更强,美竹对其出笋没有实质性影响。

表1 累计发笋数量的模型拟合结果

图5 红壳竹和美竹出笋的数量(N)与间隔时间(t)的曲线拟合
3 讨论与结论
3.1 空间格局随时间的改变
生态位分化是群落生物多样性和物种共存机制的重要依据。竞争排除理论表明,生态位相似的种群在一个区域内不能平衡,竞争能力强的一方最终会完全取代竞争能力弱的一方[16]。可以推论,生态系统中生物多样性不能维持,然而这与本研究实际情况相违背,自然界存在着各种群落,而这些群落维持生态系统中的生物多样性。因此,各种解释这种现象的理论被发表,这些理论主要分为两派,一派是基于中性理论的非稳定物种共存[17],另一派是基于生态位分化的稳定物种共存[18]。中性理论主要论述自然界中的扩散限制、物种形成和生态漂移的重要性,并提供量化零模型来评估自然选择的作用,即不同个体在生态学上可看成是完全等同的,群落结构的因素是生态漂变。这种理论可以很好地对群落结构进行预测,但其假设前提与本文研究结果相违背。因而生态位分化理论在这一研究领域占据主导地位,即群落中多个种群相互竞争与共存关系的关键是生态位分化,种群在扩散和适应过程中形成空间隔离、生活史差异等作用来避免对栖息地、食物养分等资源的竞争,从而维持种群的延续[19-20]。生态位分化在动植物种群共存机制的研究中已趋于成熟,闫海冰等[21]分析华北山地天然次生林群落中各树种的空间关联性,发现在大尺度条件下各种群的空间关联性皆不明显,且生态位分化是重要原因。梁淼等[22]分析曹妃甸近海浮游动物优势种空间生态位分化程度,揭示了该海域环境因子对浮游动物种群的影响。钟燕等[23]分析梭沙韭(Alliumforrestii)和昌都韭(A.changduense)的生态位分化原因,结果表明温度可能是昌都韭与梭沙韭生态位分化的重要因素。本研究分析红壳竹和美竹空间生态位分化,二者的空间分布存在隔离效应,一般来说,为了减缓种间竞争这种隔离效应会加深,但本试验中二者的隔离会减弱,考虑到红壳竹新笋的扩散剧烈,其竞争力远大于美竹,而本研究区域相对封闭,研究区域西边被水泥板隔断,其余三面皆是水泥地面,美竹无法通过扩散逃逸对其它空白生境进行侵占,而其自身竞争能力弱于红壳竹,照此趋势,在本研究区域红壳竹很可能会最终完全取代美竹。
3.2 生态位分化的分析方法
空间点格局的分析法近年来得到广泛的关注,很多的研究者分析群落中各种群分布类型,如樊登星和余新晓[24]采用Ripley’sK函数法进行栓皮栎林空间点格局的分析,发现在研究尺度内,栓皮栎、油松单种的空间分布格局以聚集型分布为主,而秦鹏等[25]利用空间集聚性的二阶分析法分析4种地被竹中大个体的空间分布类型,结果表明4种地被竹大个体植株较之小个体植株而言皆呈现为随机分布类型。这些研究对群落中单一种群的空间分布类型阐述的比较清晰,但对两个种群交互影响关系在空间格局上的响应研究不足。因此,介绍群落中种群交互作用的分析方法非常必要,种群空间生态位分化广泛存在昆虫、流行病和生态学领域,是相互竞争与共存的一种典型表现。而特定类型核估计的方法广泛应用于这些领域的空间分布交互关系的分析。Diggle等[8]最早提出这个方法是应用于康沃尔郡4种牛结核病空间分布关系的分析,结果表明这4种牛结合病在康沃尔郡存在显著的空间隔离,而后Lu等[26]将其应用于Bt棉田龟纹瓢虫(Propyleajaponica)和异色瓢虫(Harmoniaaxyridis)种间时空生态位分化的分析,发现2种瓢虫在时间和空间生态位上都存在显著分离。此外,Sandhu等[2]还利用此方法分析不同年龄阶段的毛竹(Phyllostachysedulis)种内空间生态位分化,发现2度竹、4度竹、6度竹和8度竹在该研究区域呈现出显著的空间生态位分离。因此,这个方法还可以应用于种内生态位分化的讨论。
本研究使用的交互类型的K函数是一个传统的用于分析两种不同类型点事件空间关系的方法,这个方法建立在Ripley提出的K函数基础上,Ripley的K函数主要强调一个种群中不同个体形成的分布关系,而本研究中交互类型K函数反映两个种群相互影响形成分布关系。目前很多研究探讨多种群空间关联性分析,例如高福元和赵成章[27]研究甘肃退化草地臭草(Melicaprzewalskyi)与阿尔泰针茅(Stipakrylovii)的空间关联性,并提出一种多元点格局的分析方法,结果显示在退化草地斑块形成、扩散、稳定阶段时所有尺度下二者空间关系为负关联,但斑块衰退阶段在38~150 cm尺度下为无关联,表明二者种间竞争减少。史宇等[28]对北京山区黑桦(Betuladahurica)次生林的点格局分析时,发现0~25 m尺度下黑桦与蒙椴(Tiliamongolica)呈负关联关系,该尺度下种间竞争激烈;卢志军等[29]对巴山木竹(Bambusarutila)发笋和大熊猫取食笋空间分布相关性分析时,发现大熊猫取食的笋0~20 m尺度上呈正相关关系,表明巴山木竹为秦岭大熊猫的主要食物来源;任珩和赵成章[30]研究高寒退化草地狼毒(Stellerachamaejasme)和赖草(Aneurolepidiumdasystachys)的空间分布及竞争关系,发现给定尺度下二者关联性从正相关到不相关再到负相关转换,种间竞争强度也逐渐增大。这些研究都使用多类型点格局的分析方法,这些研究方法包括本文中交互类型的K函数在表示方式上略有不同,但实际作用一致,都适用于研究分布于同一区域不同类型植物的空间生态关系(空间排斥、空间吸引、相互独立)。
本研究利用特定类型概率的核估计方法去检验红壳竹和美竹的空间生态位分化,结果表明,2种竹存在显著的空间分布隔离(P<0.05),符合植物种群为避免过度竞争而表现的生存策略。并且,本文在K函数的基础上使用了多种群交互关系的分析法,在给定尺度下红壳竹与美竹观测组估计值完全在下包迹线以下,说明2竹种发笋的空间分布互相排斥,但在短期内通过种间空间分布隔离实现共存,这与竹类植物竹内不同年龄群体通过空间分布隔离实现共存[2]结果十分类似,这种空间分离并不完全是物种间的主动回避,而很可能是因为弱竞争力物种被强竞争力物种的排挤通过扩散优势占据空白生境导致的结果,已有研究表明弱竞争力物种往往通过强扩散能力实现和强竞争力物种的共存[31],但在有限空间内如果没有外界干扰发生弱竞争力物种因无法进一步扩散而被强竞争力物种挤压,很可能导致其最终消亡,且这种过程发生的时间较难预测,值得进一步量化不同物种的竞争参数、扩散参数,因为这些参数的初始值会对弱竞争力物种的灭绝时间产生重要影响[31]。
