2种水培观叶植物叶面积回归测定①

刘晓荣 吴志 徐扬 韩庆斌 王代容

（广东省农业科学院环境园艺研究所/广东省园林花卉种质创新综合利用重点实验室广东广州510640）

据统计，现代人每天约有80%～90%时间在室内度过，室内空气质量对人体健康产生的影响已受到重视，《2019中国室内空气污染状况白皮书》发布中国室内空气污染严重不合格比例高达74%，室内空气污染已成为危害人体健康的头号杀手。观赏植物可净化空气中的甲醛、苯和三氯乙烯［1］；水培观赏植物不仅可以清除室内空气污染物，而且清洁、观赏性强、养护方便，在室内绿化、美化装饰中应用越来越广泛，是现代环境、植物利用等方面研究的新热点。

单位叶面积是分析植物吸收甲醛、苯等污染气体的一个重要指标［2-3］，叶面积的准确测量有重要意义。植物生理学家和农学家已经开展了许多叶面积测定的相关实验，分为离体取样测定（主要有干重法、鲜重法、叶面积仪扫描法等）和非离体测定（系数回归法、方格法、图像处理法等），离体测定叶面积需要移除叶片进行测量，比较费时且损坏植株。非离体测定中的回归方程法，具有简单易行、快速、不伤叶片等优点，也越来越被人们所重视。目前，在龙眼、香蕉、猕猴桃果树和木薯、西葫芦、甜椒蔬菜［4-6］等已有相关研究，但在观赏植物中很少进行建模研究，在水培观叶植物中更鲜有报道。

水培中比较常见的吊兰（Chlorophytum comosum）和山海带（Dracaena cambodiana），这两种植物叶片细且长，用叶面积仪测时需剪成适当的长度分段才能测出。因此，开展其非破坏性测定方法研究显得很有必要。本研究首先利用便携式叶面积仪测定叶片的长度、宽度、叶面积等叶形指标，通过叶形指标逐步回归建立叶面积的回归方程，另外一组独立数据用于模型验证。分别建立的回归方程，可在后面实际应用中，不破坏植物叶片的情况下，用尺子测量叶片的叶长、叶宽，代入相应的回归方程，即可估测其叶面积，为相关科研和应用提供叶面积统计的可靠依据。

1 材料与方法

1.1 材料

试验材料为水培观赏吊兰和山海带，植物选购于广州市花卉博览园。试验在广东省农业科学院环境园艺研究所温室内，水培条件下进行30 d的适应性培养。

1.2 方法

每个品种选择10株，每株随机取生长发育完全的叶片6片，每个品种共计60片并分别编号。用软尺测量叶长和叶宽，叶长为叶基部至最长叶尖的距离，叶宽为横向相距最远的距离。之后等分剪成2～3段，立即用Yaxin-1241叶面积仪测量叶片的叶面积。将观测得到的数据分为2组，1组用于建模，1组用于模型的外部验证。试验数据应用Excel 2010、SAS 8.1软件进行统计分析。

2 结果与分析

2.1 叶形指标

表1显示，吊兰叶面积在21.7～71.5 cm2，变异系数（CV）为26.43%；叶片长2.17～4.60 cm，变异系数为16.43%；叶宽0.15～0.29 cm，变异系数为15.48%；叶长：叶宽比值为9.74～19.42，变异系数为14.78%。表明叶长、叶宽和叶长：叶宽差别不大，叶面积变异最大。

表1 吊兰和山海带叶片特征

山海带叶面积在6.71～82.33 cm2，变异系数（CV）为33.07%；叶片长2.08～5.51 cm，变异系数为16.87%；叶宽在0.10～0.21 cm，变异系数为16.38%；叶长：叶宽比值为21.89～30.96，变异系数为7.69%；表明叶长和叶宽差别不大，叶长：叶宽变幅最小，叶面积变幅最大。

2.2 叶形指标间的相关性分析

从表2可以看出，吊兰和山海带叶面积与叶长/叶宽之间的相关系数分别为0.047 64、0.139 83，在5%水平没达到显著相关。叶长、叶宽、叶片鲜重和叶片干重与叶面积之间高度相关；叶片鲜重与叶面积之间的相关系数大于叶长和叶宽与叶面积之间的相关系数。

表2 吊兰和山海带叶面积与形态指标间的相关性

2.3 数学模型的预测

通过逐步回归法筛选了3步吊兰叶面积，达到了最优的逐步回归模型，最终入选的变量有L、D和P，得到预测吊兰叶面积的模型（式1））。决定系数R2为0.977 6，Cp值为6.270 0。

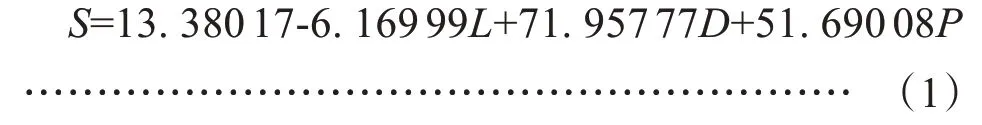
山海带叶面积通过逐步回归模型筛选了8步，达到了最优的逐步回归模型，最终入选的变量有W、F、D和P，得到山海带叶面积的预测模型（式2）。决定系数R2为0.988 6，Cp值为4.076 0。

2.4 数学模型的验证

基于模型预测叶面积的外部验证结果如图1～2。吊兰叶面积的预测值（x）与实测值（y）的回归方程式y=1.488 9+0.953 16x，R2=0.910 9，AdjRsq为0.908 7，相关系数r为0.954 40，均方根误差RMSE为4.808 6，表明模型预测的准确性。

山海带叶面积的预测值（x）与实测值（y）的回归方程如式y=0.933 9x+2.856 2，R2=0.978 7，AdjRsq为0.978 3，相关系数r为0.989 32，均方根误差RMSE为1.928 9，表明模型预测的准确性。

3讨论

单位叶面积是分析观叶植物吸收甲醛、苯等室内污染物的一个重要生物学指标，叶面积的大小是计算植物净化室内空气净化率的一个关键因子。研究并建立一个准确、快速，不破坏叶片生长的叶面积估算法，可以有效地应用在植物对甲醛、苯等吸收效率筛选上，为利用室内观叶植物去除室内有害物质提供依据，这在室内植物配置上具有重要的现实意义。

便携式叶面积仪，可直接测量叶片长度、宽度、周长、叶面积等叶形指标，但测量时操作要求规范，且测定时采摘的大量叶片会直接破坏植株生长，对于叶形狭长叶片还须处理剪成适当的长度测量，不仅破坏叶片植株，也影响测量地准确性。

叶面积与叶片各形态特征值间均具有相关性，吊兰和山海带叶面积与叶长、叶宽、叶长×叶宽之间均呈极显著相关，逐步回归分析结果显示，变量（叶长×叶宽，叶干重）是吊兰和山海带共有的两个变量。叶长×叶宽是叶面积估测的一个重要指标，这在龙眼、杂种臻和石斛组培苗上也有相似的研究结果。本研究中叶面积与叶长/叶宽相关性不显著，而对龙眼两个品种研究显示，其叶面积与叶长/叶宽有极显著地相关性。

基于模型预测叶面积的外部验证、叶估算面积与实际面积的相关性检验，证明在吊兰和山海带上建立的叶面积估算预测准确性高，可在实际上应用；本实验未统计总叶片数，无法建立与整株总叶面积模拟函数，估算整株总叶面积；水培观叶植物品种繁多、叶片形状各异，且栽培造型不一。因此，对水培观赏植物叶面积估算方法的探讨和建立，今后还应针对不同的品种、不同的苗龄，不同的株形及叶片总数做进一步地深入研究，分别建立合适的模型估算方法。