新的多变量特殊多项式及其在量子光学中的应用

孟祥国吴孟艳孙程美

(聊城大学 物理科学与信息工程学院，山东省光通信科学与技术重点实验室，山东 聊城 252059)

0 引言

作为一类常用的特殊多项式，埃尔米特多项式在数学和物理上都扮演着重要角色，这是由于它具有正交性、完备性等一系列有意义的基本性质，并涉及一些重要的关系式，如产生函数、多项式乘积、递推关系和微分关系等。

单变量埃尔米特多项式Hn(x)可由它的产生函数来定义[1]，即

或者

多项式Hn(x)不仅能帮助求解量子谐振子的本征态和分数阶傅里叶变换的本征函数[2]，还也可以方便导出算符Fredholm 方程的解析解，以及处理耦合谐振子系统和推广角动量系统的本征值问题[3-5]。对于双变量情况，埃尔米特多项式Hn，m(x，y)定义为[6]

其偏微分表示和幂级数展开式分别为

物理上，Hn，m(x，y)可作为受迫谐振子动力学中粒子数态的跃迁振幅和二维复分数傅里叶变换的本征函数[2，7]，同时也能为研究Bargmann变换、量子纠缠现象和二次指数介质中的Talbot效应提供帮助[8]。此外，单双变量的埃尔米特多项式也经常被应用于导出一些新的渐近公式，玻色算符恒等式以及制备一些能作为关键量子信息源的新非高斯纠缠态[9-11]。因此，有关单双变量的埃尔米特多项式的理论研究受到极大关注。目前，人们陆续提出了一系列变形的埃尔米特多项式，如退化埃尔米特多项式、全纯埃尔米特多项式和q变形埃尔米特多项式[12-14]，并广泛应用于概率论、图论、数论以及数学物理的其他领域。

类似于双变量埃尔米特多项式的定义与其产生函数的关系，本文基于普通的单双变量埃尔米特多项式及其微分关系式，导出两个新的多变量特殊多项式，给出它们的产生函数以及一些新的微分恒等式，并详细讨论它们在计算多光子增加单双模压缩态的归一化因子和维格纳函数中的具体应用。

1 新的多变量特殊多项式

1.1 三变量特殊多项式

假定指数函数exp(－s2－τ2＋ϑsτ＋sx＋τy) 为新的特殊多项式Fn，m(x，y；ϑ) 的产生函数，类似于式(4)，有

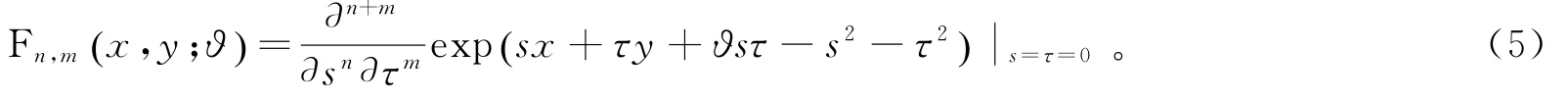
根据单变量埃尔米特多项式Hn(x)的定义式(1)，则

进一步，利用微分恒等式H′m(x)＝2mHm－1(x)，则式(6)变为

可见，Fn，m(x，y；ϑ) 为一个新的三变量特殊多项式，其级数展开式为两个单变量埃尔米特多项式之积的叠加形式，且其产生函数为

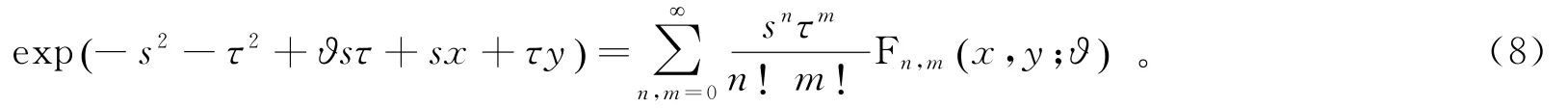
特殊地，当ϑ＝0时，多项式Fn，m(x，y；ϑ) 变为两个单变量埃尔米特多项式之积，即进而，利用微分恒等式

可导出多项式Fn，m(x，y；ϑ) 关于变量x，y的一阶偏微分方程

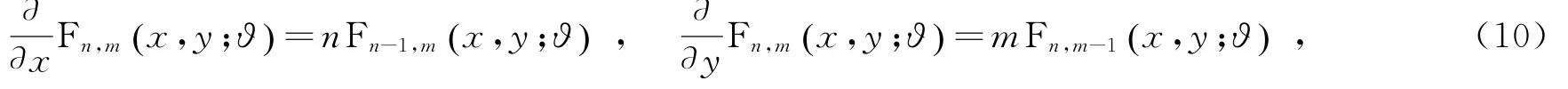
进而，关于多项式Fn，m(x，y；ϑ) 的高阶偏微分方程为

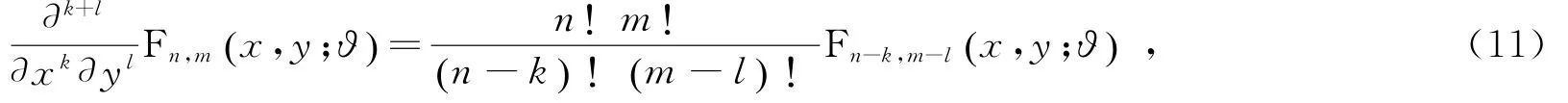
它在形式上类似于普通的双变量埃尔米特多项式Hn，m(x，y) 的高阶偏微分方程。

1.2 六变量特殊多项式

同样，假定指数函数exp(－sτ－s′τ′＋vss′＋υττ′＋xs＋x′s′＋yτ＋y′τ′) 为新的特殊多项式Gn，m，l，k(x，y，x′，y′；v，υ) 的产生函数，类似于式(4)，有

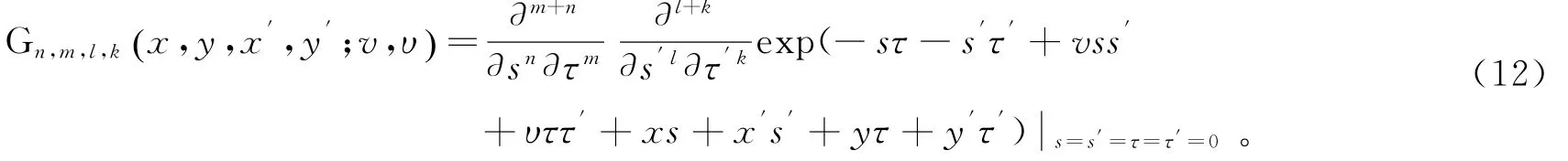
根据式(4)中双变量埃尔米特多项式Hn，m x，y() 的定义，可得到

进一步，利用关于双变量埃尔米特多项式Hn，m x，y() 的微分恒等式

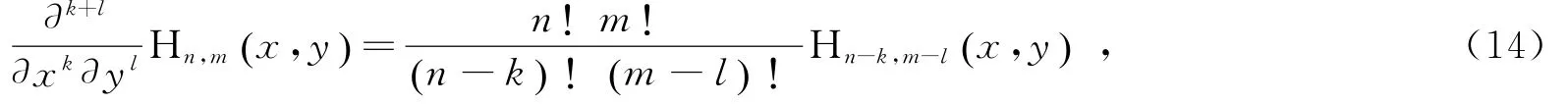
式(13)自然被改写为

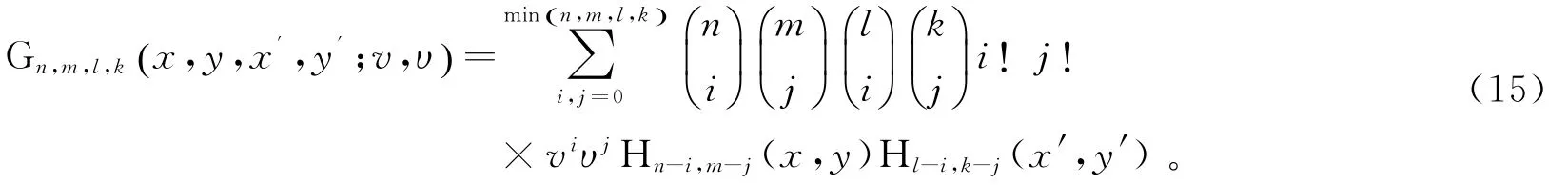
同样可见，Gn，m，l，k(x，y，x′，y′；v，υ) 为一个新的六变量特殊多项式，其级数展开式为两个双变量埃尔米特多项式之积的叠加形式，且其产生函数为

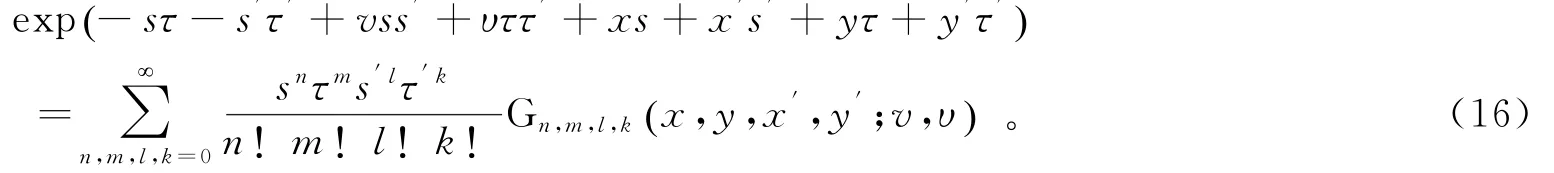
类似地，利用埃尔米特多项式Hn，m x，y() 的微分关系式(14)，得到特殊多项式Gn，m，l，k(x，y，x′，y′；v，υ)关于变量x，y，x′和y′的高阶偏微分方程，即

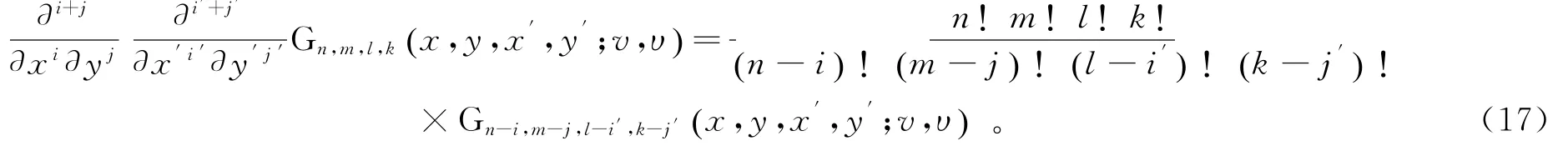
2 多变量特殊多项式的具体应用

2.1 归一化

量子态的归一化是量子光学中非常重要的一个问题。对于量子态的实验制备，归一化因子用来刻画态的成功制备概率，并能进一步帮助探查该量子态的基本性质和物理应用。

理论上，当把产生算符a†(即单光子增加操作)重复作用到压缩真空态时，可实现多光子增加压缩真空态a†mS(r)|0〉 。实验上，利用弱耦合条件下的非简并光学参量下转换(parametric down-conversion，PDC)过程可实现单光子增加操作[15]。在目前实验条件，在单光子增加操作次数m较少的情况下，多光子增加压缩态有可能实现制备。态的归一化因子为

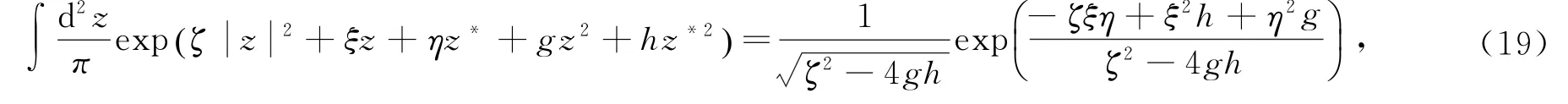
可有

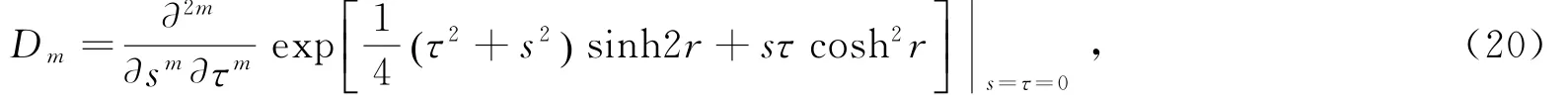
通过与多项式Fn，m(x，y；ϑ) 的产生函数比较，可知

特殊地，当m ＝0 时，F0，0(0，0；－2 tanh－1r)＝1，这样D0＝1，如同期望的一样；而当m ＝1 时，F1，1(0，0；－2 tanh－1r)＝－2 tanh－1r，故D1＝sinh2r，这恰好为态的归一化因子。

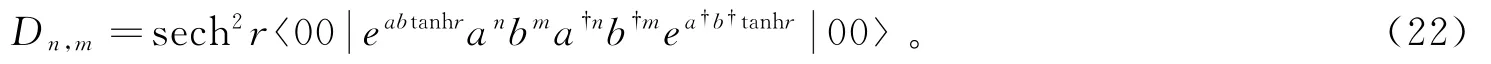
进一步，根据六变量特殊多项式G n，m，l，k(x，y，x′，y′；v，υ) 的定义，则归一化因子D n，m简化为

当n＝m＝0时，G n，m，n，m(0，0，0，0；－tanh－1r，－tanh－1r)＝1，D0，0＝1，对应于压缩态的归一化因子。

2.2 维格纳函数

维格纳函数是一种非常有用的工具，它能从相空间的角度全面深入地描述非经典态。利用多变量特殊多项式及其产生函数，能简化处理一些量子态的维格纳函数，并为分析它们的非经典性质提供方便。一般来说，量子态ρ的维格纳函数定义为W(α)＝trρ[ Δ(α)] ，式中

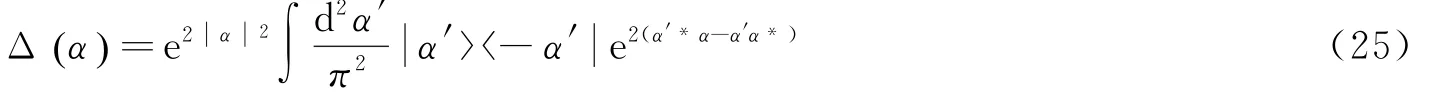
为单模维格纳函数的相干态表示[17，18]，为单模相干态[19]。因此，利用式(25)，可把态的维格纳函数表示为

进一步，利用数学积分公式(19)，可有

再利用特殊多项式Fn，m(x，y；ϑ) 的定义式，可得到

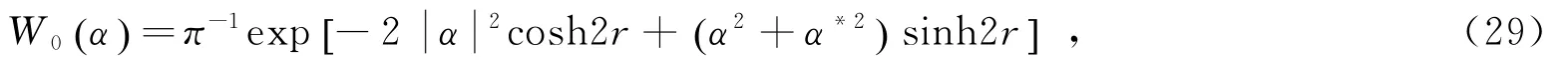
重复使用数学积分公式(19)和六变量特殊多项式的定义式(12)，可得到

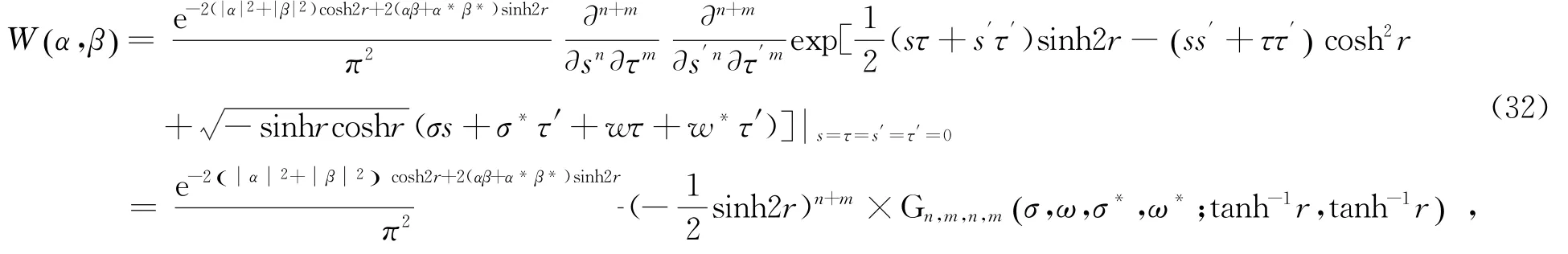
式中

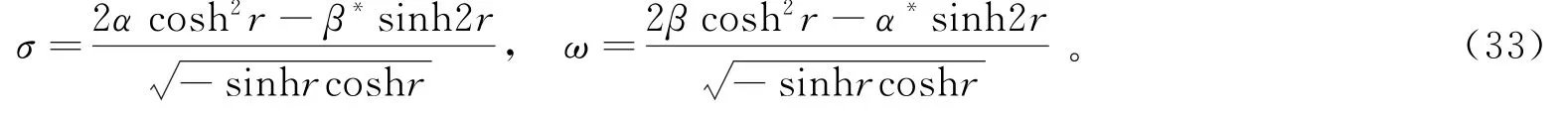
特殊地，当n＝m ＝0时，式(33)退化为双模压缩态的维格纳函数，即

3 结论

综上，本文充分利用普通的单双变量埃尔米特多项式的定义式及其微分关系式，推导出了两个新的多变量特殊多项式，即三变量特殊多项式和六变量特殊多项式，并给出了它们的产生函数以及一些新的微分恒等式。作为这两个新的特殊多项式的应用，解析推导出了多光子增加单双模压缩态的归一化因子和维格纳函数，发现它们恰好都与新的多变量特殊多项式有关，从而避免了繁琐的高阶偏微分运算。