数字化集成信息增量学习算法仿真研究
2022-08-22孔凡功陈洪雷
赵 鑫,刘 玉,孔凡功,陈洪雷
(齐鲁工业大学山东省科学院生物基材料与绿色造纸国家重点实验室,山东 济南 250353)
1 引言
增量学习是指不断学习的过程,在学习过程中,可接受新知识并对历史学习知识实现保存。在实际应用过程中,数据量几乎是累积增加状态,在新数据处理时,增量学习通常用于数据库巨大以及数据不断增加形成的数据流处理[1]。当下数字化数据库已经成为各个企业以及各领域主要数据存储方式,数字化数据库可实现数字数据、资源以及信息的集成,且该类数据库内的数据具备不断增加特征[2],该类数据在不断累积过程中,需要采用相关有效方法处理,保证数据中的数据对象、结构、关系等,可有效进行分类、聚类以及重组等[3]。大量数据在存储过程中,会出现爆炸式增长,导致增量学习效率较低、数据分类精度降低。
因此,为了更好实现数字化集成信息增量学习,本文以深度学习算法中的朴素贝叶斯概念为依据,研究基于加权朴素贝叶斯分类的数字化集成信息增量学习算法,完成数字化集成信息增量学习,保证数据集中数据的最佳分类效果。
2 数字化集成信息增量学习算法
2.1 加权朴素贝叶斯的增量分类模型
加权朴素贝叶斯算法是以后验概率获取样本类别标签,其中后验概率的获取是通过先验概率和条件概率实现,前者属于训练的样本类,后者属于特征项的类[4]。为实现信息扩充、增加信息量的丰富程度,以此保证对数字化集成信息增量的分类效果,特征项采用两种属性的相似度描述,分别为条件和决策,实现较小的训练子集,提升增量学习效率。
两种属性的定义分别为:
(u1(x),u2(x),…,un(x))表示特征向量,且维数为n,用其描述数据集x,其中ui(x)表示取值,属于x的第i个属性。若条件和决策两种属性分别为ui和uk,以后者为参照,前者相对于其的相似度公式为
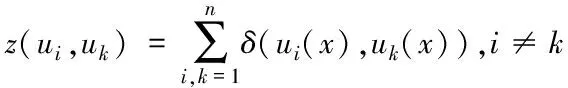
(1)
其中
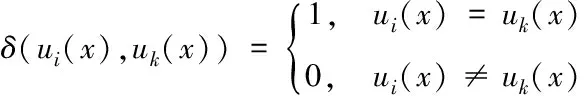
(2)
式中:δ(ui(x),uk(x))表示函数,用于完成属性数量的统计,其为相等取值,属于ui和uk两者。
设训练样本集和测试集分别用D和Dt表示,两者均为给定量,uk和ui间的相似度通过式(1)获取,前两者属于Dt,后者属于D,且后者为各个条件属性。Ak的属性权值,采用计算结果表示,用Wk表示,完成加权朴素贝叶斯分类的生成,同时获取分类结果[5]。
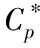
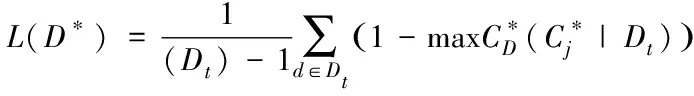
(3)
基于加权贝叶斯分类算法步骤如下所述:
输入:D和Dt;
输出:dt的类别。
步骤1:分类器C的学习通过D完成。
步骤2:返回分类器的条件为Dt≠0,反之继续。
步骤3:若Dt中的各个元素dtp∈Dt,则表示L=0。
重复:
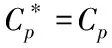
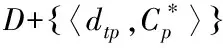
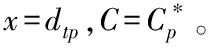
步骤4:若D=D+{〈x,C〉},Dt=Dt{dtp},则反之步骤1。
2.2 数字化集成信息增量学习
设V和I分别表示原始数据集和增量集,且前者为2.1小节挖掘的分类结果的集合,若两者均满足V∩I=∅条件,对两者训练,且在V上完成,使其形成数个初始加权朴素贝叶斯分类器和其集成,获取加权朴素贝叶斯分类器集成,且需在样本集合V∪I上,是算法最终目标[6,7]。
利用随机属性方法在初始化时,实现一组属性子集的随机形成,其为完全属性集中,并属于原始数据库中,在保证训练集中样本数量不发生变化的情况下,训练形成的所有加权朴素贝叶斯分类器均一一和各个子集相对应[8]。
基于随机属性选择形成加权朴素贝叶斯分类器算法的获取,是以条件属性集S为基础实现:
1)建立贝叶斯概率表,并且在V中完成。
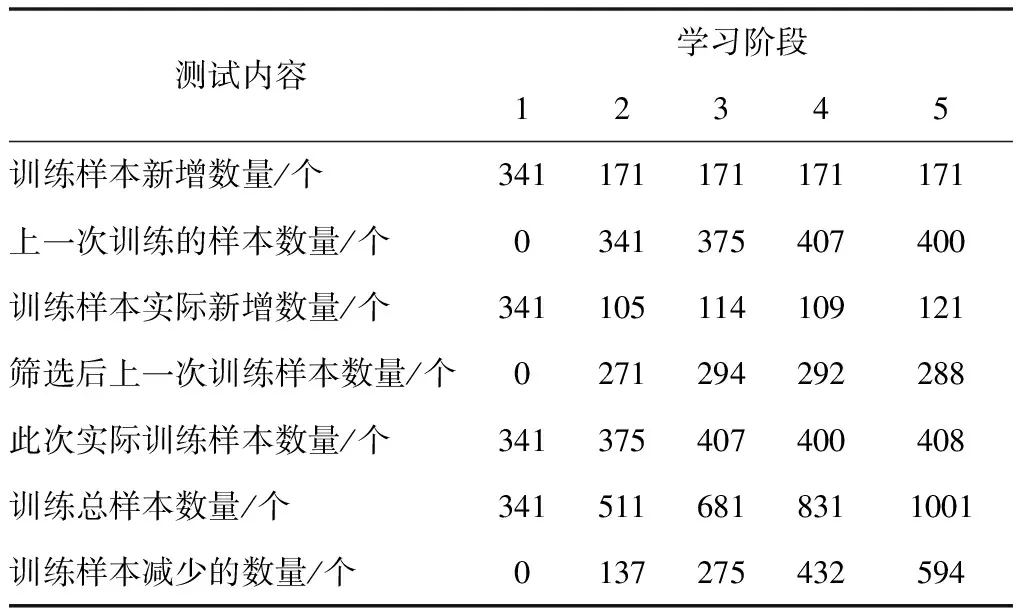
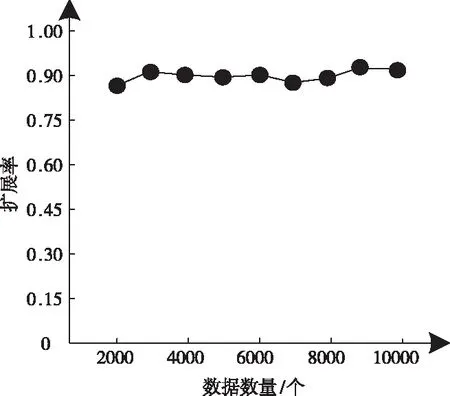
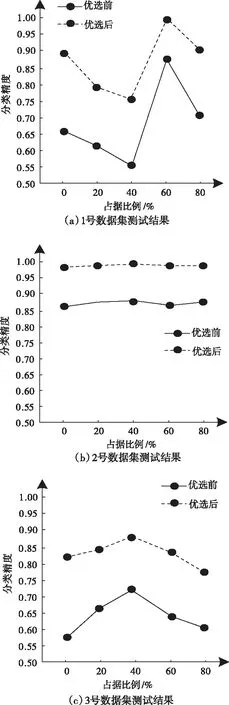
2)为形成随机子空间,维数为m*,且属于条件属性,该属性维数为m,需获取S中m*个条件属性,且在概率P相等的情况下随机得出,并位于V中。其中,P∈(0,1),m 3)为获取数量为ω个的属性子集,将上一步骤重复操作ω次,使各个子集完全加入决策属性中,次数属性数量为m*+1。 4)以贝叶斯概率表B为依据,完成数量为ω的加权朴素贝叶斯分类器的生成,且需在上述子集的基础上。 B在构建过程中,在其参数取值范围的分布状态为均匀状态,是由于参数呈现无信息先验分布状态导致。因此,以无信息Dirichldt共轭先验假设为标准[9],求解V的两个参数,分别为θi、θjk|i,两者计算公式分别为 (4) (5) 式中:countV(x)表示计数器,用于统计Sj可能存在的取值数量,且为第j个;ajk表示取值,属于Sj,且为第k个;|Sj|表示取值个数,且属于Sj;Q表示离散值,且Q={q1,q2,…,qi}。 由于通过选取方式为随机选取,且在等概率情况下,因此,获取的m*存在差异,且属于属性子集。I的自动分组是根据是否存在类别标签,并在增量学习阶段,I1和I2则为划分后的两组,其中,具备类别标签的样本属于前者,没有类别标签的样本属于后者中。先对I1中的样本学习,以原有的顺序,通过加权朴素贝叶斯分类器展开学习[10],以无信息Dirichldt共轭的分布为依据,更新参数,为 θ′jk|i=P(Sj=ajk|q=qi) (6) (7) 式中:δ=|Q|+|V|+|Ii|。 通过上述步骤即可获取加权朴素贝叶斯分类器的更新,且数量为w,采用遗传算法选取获取最优结果,可得出数字化集成信息增量学习结果。算法整体流程步骤如下所述: 1)为实现数个加权朴素贝叶斯分类器的生成,需依据上述2.2小节的获取方法得出。 2)完成I的自动分类,且需依据样本是否存在标签得出,划分成I1和I2。 3)完成I1和I2的学习,且通过各自适合的顺序完成。 4)以数据子集表为依据,完成加权朴素贝叶斯分类器参数的更新。 5)为获取更新后加权朴素贝叶斯分类器的最佳结果,采用遗传算法完成。 6)当有新样本x*输入时,统计遗传算法获取的输出类别结果,数量最多的结果计为y*,其公式为 (8) 式中:SBCj表示更新后分类器。 遗传算法在运算过程中,初始集成中的分类器数量即为其算法的编码尺寸;将比例选择和两点杂交,分别用于选择算子和交叉算子,但是,在适应度排序最高的前百分之十的个体不参与上述两种操作,且该适应度属于各代遗传群体中,可实现自动保存至下一代中,若I1为空集,表示可将所有的分类器简化成简单集成。 为验证本文算法应用效果,选取某机器学习库中的数据集作为实验分析测试对象,将该数据集分别编号为1号~3号。三个数据集的依次详细情况为: 1号数据集:属性数量36个、类别数量2个、样本数量3196个、D数量/个1599个、I1数量959个、I2数量638个; 2号数据集:属性数量22个、类别数量2个、样本数量8124个、D数量/个4064个、I1数量2436个、I2数量1624个; 3号数据集:属性数量9个、类别数量2个、样本数量958个、D数量/个481个、I1数量286个、I2数量191个。 上述共有数据样本数量12278个,类别数量6个,属性数量67个,分类器数量25个,群体种群规模100,交叉概率0.59,变异概率0.01,最大迭代次数55次。针对3个编号的数据集,采用分层随机抽样方式完成训练、验证和测试样本的划分,三者比例分别为70%、15%、15%。完成各个样本的精度估计后,所有分类器均需完成子集的重新学习,为下次增量学习提供可靠参数。 测试文本算法在增量学习过程中的学习效率,在不同的训练阶段,通过新样本选择性加入的方式,测试算法的训练性能,见表1。 表1 算法训练性能测试结果 分析表1中数据可知:在学习增量训练学习阶段的不断增加,从第一阶段直到第五阶段整个过程中,训练样本减少的数量明显提升,从最开始数量没有减少,到减少数量达到594个的数据结果可表明,本文算法可描述特征项采用两种属性的相似度,实现较小的训练子集,使训练样本数量被有效划分并逐渐减少,以此可提升算法的增量学习效率。 为进一步分析本文算法的性能,采用数据伸缩度和扩展率作为衡量指标,前者用于衡量算法的时间复杂度,后者用于衡量算法在运行过程中对不同大小数据集的适应性,测试结果见图1、图2。 图1 数据伸缩度测试结果 图2 扩展率测试结果 根据图1和图2测试结果可知:数据数量的增加,数据伸缩率呈上升趋势,数据数量在4000个以下时,数据的伸缩率上升相对较为平缓,当其数量超过4000个以后,伸缩率上升增加幅度明显提升,因此,算法可根据数据的大小调整数据的伸缩情况;除此之外,随着数据数量的增加,算法的扩展率呈现相对平稳变化,数据量为2000个时,扩展率为0.87,数据量为10000个时,扩展率为0.94,该结果差距较小,表明算法可较好地适应不同大小数据集,有效保证算法计算结果。 为测试本文算法对于数字集成化信息增量学习的应用效果,选取1-3号数据集,测试本文算法通过遗传算法优选后的数据集成分类精度和未进行集成分类精度的结果对比,分析本文算法的优势,结果见图3。 图3 三种数据集的测试结果 分析图3的测试结果可知:在没有类别标签样本占据比例发生变化的情况下,三种数据集的优选前和优选后结果均呈现差异化的变化趋势,根据整体测试结果可看出,在相同占据比例情况下,采用遗传算法优选后,数字集成化信息增量学习的分类精度高于优选前,可更好保证其增量学习效果。 本文提出基于深度学习的数字化集成信息增量学习算法,对分类器完成当前增量学习,更好的实现数字化集成信息的分类处理,并通过一系列的测试表明:本文算法有效完成数据集的划分,提升其对数字化集成信息的分类效果,同时,算法可根据数据集的大小情况自行完成处理,避免数据量较大时,出现效率较低问题,具备较好地数据伸缩度,并且经过优选后,算法的分类精度显著提升。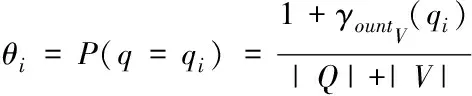
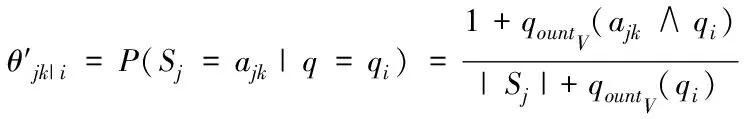
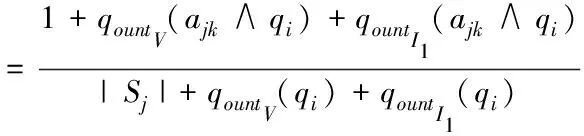
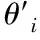
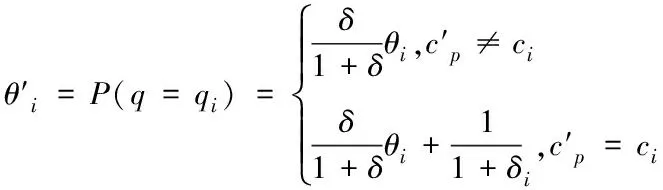
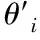
2.3 算法整体流程
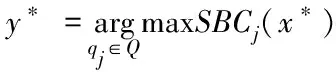
3 实验验证与结果分析

4 结论
