一个新三维混沌电路设计及其同步控制*

闫少辉，施万林，宋震龙，王尔童，孙 溪，黄羿博

(1.西北师范大学物理与电子工程学院，甘肃 兰州 730070; 2.甘肃省智能信息技术与应用工程研究中心，甘肃 兰州 730070)

1 引言

自1963年气象学家Lorenz[1]发现了第一个混沌吸引子以来，混沌理论的研究和应用在非线性科学领域获得了极大发展。混沌可以由非线性微分方程的简单数学模型产生，其不可预测性和高度伪随机性等特性使其在保密通信中得到了广泛应用[2,3]。因此，设计和实现具有理想特性的混沌系统具有非常重要的理论价值和实践意义。

在Lorenz系统的基础上，国内外研究人员相继提出了一系列新的混沌系统。例如，陈关荣教授发现的Chen系统具有与Lorenz类似但拓扑不等价的新型混沌吸引子[4]；2002年，吕金虎等人[5]提出了Lorenz系统与Chen系统之间的临界系统，并将其命名为Lü系统。近年来，在上述系统的基础上也有许多新的混沌系统不断被提出。文献[6]提出了一个新的三维自治混沌系统，该系统方程包含多个非线性项，而在物理实现中，二次非线性和常数项需要乘法器和直流偏置电压来实现，使得电路变得复杂。文献[7]提出了一个三维连续混沌系统，该系统在x-y平面上的吸引子与Lü系统的相同，其吸引子关于z轴对称。因此，设计电路简单但动力学行为复杂的混沌系统成为了当前的研究重点。

混沌保密通信一直以来都是非线性科学领域研究的热点，而混沌同步是实现混沌保密通信的关键。近年来，人们相继提出了一系列混沌同步控制方法。文献[8]在新构建的四维超混沌系统和四维超混沌Chen系统之间设计了广义同步控制器，从而实现了广义同步。文献[9]应用主动控制同步法和自适应控制同步法来设计各自不同的控制器，使得响应系统和驱动系统达到同步。文献[10]利用自适应控制方法实现了衍生系统之间的同步以及非衍生系统之间的同步。尽管上述文献都较好地实现了系统之间的同步，但也导致系统结构更复杂，电路实现更困难。因此，简化电路结构，研究控制精确且规则限制少的同步方法将变得尤为重要。

本文基于Bao系统[11]构建一个新的三维混沌系统。不同于经典Bao系统，新系统产生的混沌吸引子均不对称，系统具有更复杂无序的混沌特性和新的拓扑结构。通过对该系统的动力学特性研究，结合不同参数下的Lyapunov指数谱和分岔，分析不同参数对该混沌系统的影响，证明该系统具有丰富的混沌特性。此外，通过计算谱商SE(Spectral Entropy)复杂度和C0复杂度，为电路参数配置提供了一种直观有效的方法。同时，在Multisim软件上对系统电路进行设计与仿真，实验结果与数值仿真结果相一致。最后，通过非线性反馈与线性反馈同步控制方法分别实现系统的同步，数值仿真与电路仿真结果验证了系统的可行性。

2 新系统模型与动力学特性分析

2.1 新混沌系统模型

本文根据Lü系统和Liu系统[5]的构建模式，在Bao系统的基础上构建一个新的三维混沌系统。新混沌系统的数学模型如式(1)所示：

(1)

其中，a，b，c，d为系统参数。当选取系统参数a=20，b=14，c=11，d=5，变量x,y,z的初始值为 (1，1，1)时，利用Matlab对混沌吸引子进行了数值模拟。时间步长设置为0.01 s，时间长度设置为50 s。图1a为三维空间吸引子及其在不同平面上的投影图。由图1a可见，系统(1)的吸引子轨迹关于坐标轴均不对称，并且其轨迹在特定区域存在遍历性[12]，说明该系统具有新的拓扑结构。图1b为3个变量的时间序列，其时域波形都是非周期的。图1c为系统在y=0上的Poincare截面，其轨迹为一条没有闭合的线段且具有自相似的分形结构[13]，说明系统是混沌振荡的。通过0-1测试，得到呈不规则分布的p-s运动轨迹,如图1d所示，计算可得渐近增长率K的值为0.996 3 (K≈1)，表明系统具有混沌特性。

Figure 1 Dynamic behavior of the new chaotic system图1 新混沌系统的动力学行为

2.2 耗散性与平衡点稳定性分析

对于构建的新系统 (1)，有如式(2)所示的等式：

(2)

其中，V表示相位体积，当a=20，b=14，c=11，d=5时，divV=-a+c-d=-14<0，所以系统是耗散的，并且以指数形式 dV/dt=e-14t收敛 ，即当t→∞时，系统轨道的所有体积元都会以指数e-14收缩到0。因此，相空间轨线经过多次折叠和拉伸其运动轨迹最终会固定在一个吸引子上，说明吸引子是存在的。

令非线性系统模型(1)的右边等于0，如式(3)所示：

(3)

求解式(3)，可得系统有3个平衡点：P0=(0,0,0),P1=(12.155,-15.470,35.714)和P2=(-9.069,11.542,35.714)。系统 (1)在平衡点P0处的雅可比矩阵如式(4)所示：

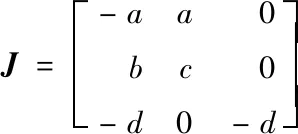
(4)

由此可以推导出特征方程如式(5)所示：

P0(λ)=λ[(a+λ)(c-λ)+db](d+λ)=0

(5)

当选取参数a=20，b=14，c=11，d=5时，由式(5)可得，系统 (1)在平衡点P0=(0,0,0)处的特征根为：λ11=-5，λ12=18.309，λ13=-27.308。由于特征值λ11和λ13为负实数，λ12为正实数，这种具有2个稳定流形和1个不稳定流形的汇合点称为鞍点[14]，因此P0是一个在二维空间中不稳定的鞍点。

将系统在平衡点P1处线性化，其雅可比矩阵如式(6)所示：

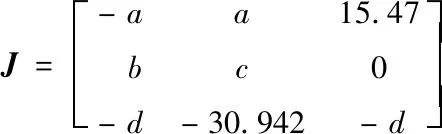
(6)

令det(J-λE)=0，解其特征根为：λ21=-30.2,λ22，23=8.1±6.74i。由于λ21为负实数，且λ22和λ23均是实部为正的共轭复数，因此平衡点P1为不稳定的鞍焦点。同理，在平衡点P2处，求其特征根为：λ31=-31.9,λ32=4.3,λ33=13.61。由于特征值λ31为负实数，λ32和λ33为正实数，因此平衡点P2为不稳定的鞍点。

2.3 系统参数对动力学特性的影响

随着系统参数的变化，系统将处于不同的混沌状态并呈现出不同的动力学行为[15]。固定系统参数a=20，b=14，d=5，变量x,y,z初始值设为 (1，1，1)，选取系统参数c作为分岔参数，当c在 (4，16)内变化时，系统(1)的Lyapunov指数谱和关于变量x的分岔情况如图2所示，其中，L1，L2和L3为Lyapunov指数谱。

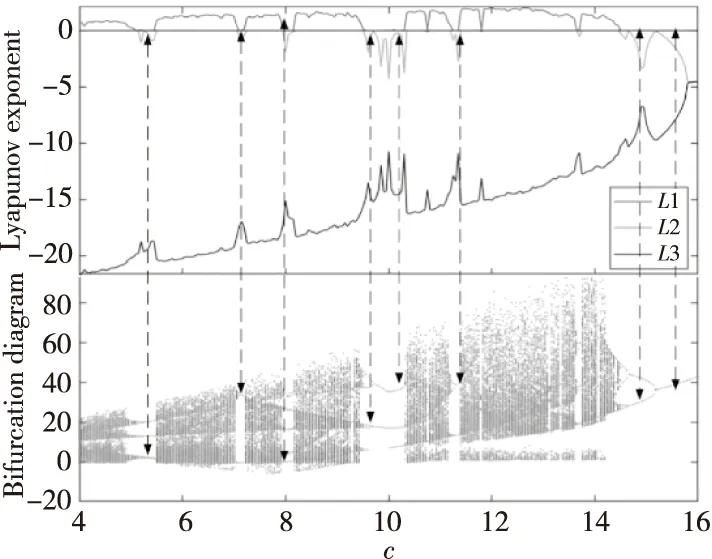
Figure 2 Lyapunov exponent and bifurcation diagram with parameter c varying in the range of (4,16)图2 参数c在(4，16)内变化的Lyapunov指数谱与分岔图

由图2可见，系统存在着各种脱离混沌的分岔路径，在路径中存在混沌与周期的复杂交替，但混沌带中依然夹有一些周期窗口。当c在 (4，16)内变化时，系统从倍周期开始脱离混沌。同时，参数c取不同值时的吸引子相图如图3所示，当c=15时，系统为极限环，当c=14.8时，系统为二周期，当c=14.6时，系统为四周期，当c=14时，系统为混沌振荡。此时系统的最大Lyapunov指数大于0。

Figure 3 Attractor phase diagram with different values of parameter c 图3 参数c取不同值时的吸引子相图

固定系统参数a=20，b=14，c=11，变量x,y,z初始值为 (1，1，1)，选择d作为分岔参数，当d在(0，12)内变化时，图4给出了变量x对应的Lyapunov指数谱与分岔图。由图4可见，该系统的轨道在这一部分有很多不同的周期和混沌跳跃，并且系统也是从倍周期开始脱离混沌，说明 Lyapunov指数谱和分岔图有较好的一致性。此外，图5显示了吸引子的相图，详细展示了从周期到混沌的演化过程。当d分别取6，8.6，9.6和10时，系统 (1)从混沌振荡(图5a)开始，到四周期振荡(图5b)，到二周期振荡(图5c)，再到极限环(图5d)。

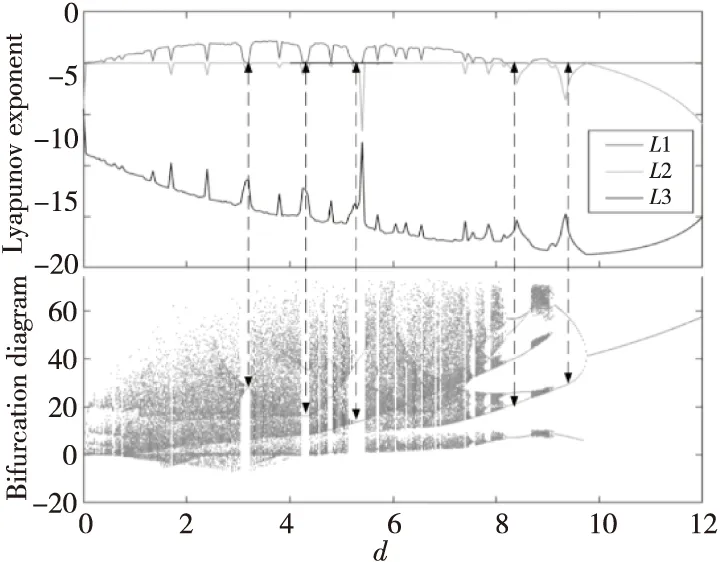
Figure 4 Lyapunov exponent and bifurcation diagram when parameter d changes within (0,12)图4 参数d在(0，12)内变化时的Lyapunov指数谱与分岔图

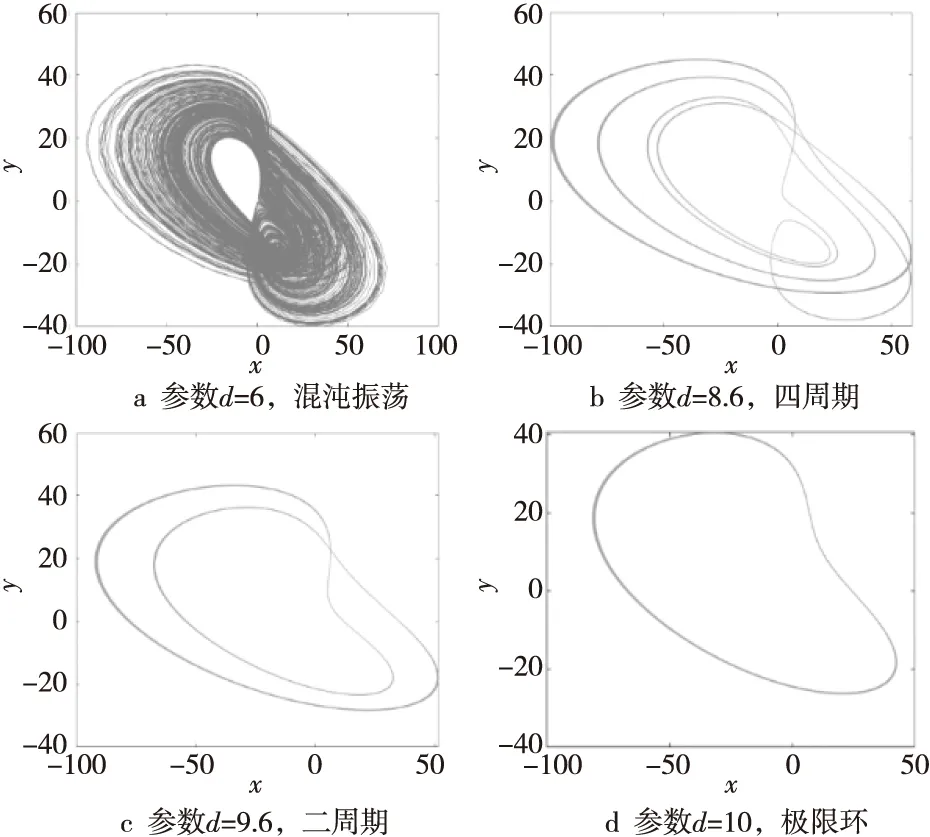
Figure 5 Attractor phase diagram with different values of parameter d 图5 参数d取不同值时的吸引子相图

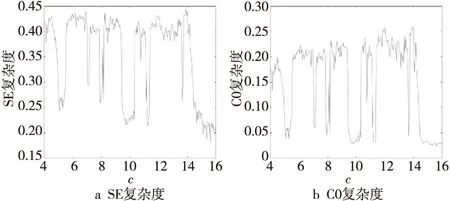
Figure 6 System complexity with the change of parameter c图6 参数c变化时系统的复杂度

2.4 SE复杂度与C0复杂度分析

系统复杂性测度对混沌系统动力学分析具有重要意义，大量研究表明，混沌系统的复杂度越高，越适合用于保密通信[15,16]。SE复杂度反映了傅里叶变换域的无序状态，谱越平坦，其SE复杂度越大，说明时间序列的复杂性越高。C0复杂度也是基于离散傅里叶变换，但它反映序列中不规则的比例[17,18]。计算系统的SE复杂度与C0复杂度与图3中的Lyapunov指数谱和分岔图中所使用的参数c相对应，如图6所示，当系统处于周期振荡时，对应的SE复杂度与C0复杂度较小，说明此时系统复杂度较低。当系统处于混沌状态时，对应的SE复杂度与C0复杂度较大，此时系统复杂度较高。由此可见，系统复杂度与Lyapunov指数谱和分岔图的变化趋势相一致。

系统随参数d变化的复杂度如图7所示。从图7可以看出，系统的SE复杂度与C0复杂度与图4的Lyapunov指数谱和分岔图的变化趋势相一致，当d大于9时，系统处于周期振荡，SE复杂度与C0复杂度较小，此时系统的复杂度较低。当选取的参数d使得系统处于混沌振荡时，对应的SE复杂度与C0复杂度较大，此时系统复杂度较高，即系统的混乱性越高。因此，SE复杂度与C0复杂度图可以提供一种直观、有效的参数配置方法。

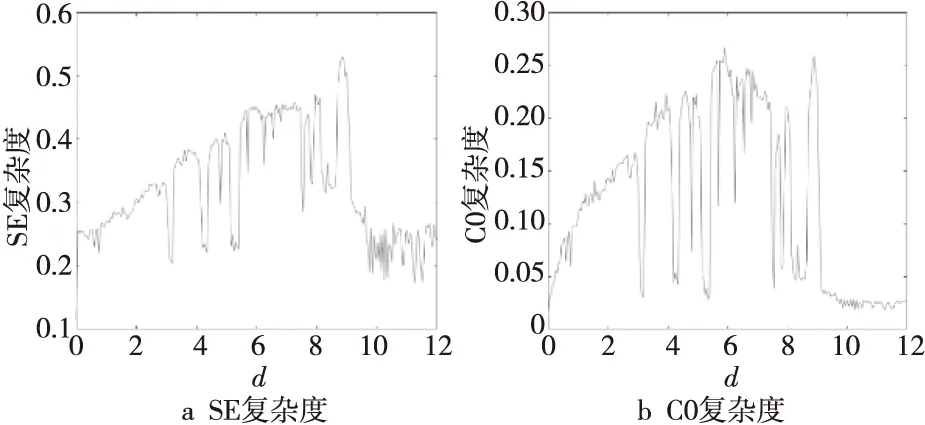
Figure 7 System complexity under the change of parameter d图7 参数d变化时系统的复杂度

在实际应用中，SE复杂度和C0复杂度的混沌图可以更好地为参数的选择提供依据。图8给出了参数c和d同时变化时SE复杂度与C0复杂度的混沌图，在复杂度混沌图中，颜色越深表示复杂度越高。在保密通信领域，复杂度越高表示随机性越大，序列恢复的难度越大。因此，混沌系统在实际应用中，应尽可能地增加其复杂性，以保证扩频系统具有良好的抗干扰性和较强的抗截获性。在图8中，选择混沌程度较高的参数时，应考虑图中间与左边的参数，而沿右边界的参数对任意的敏感程度较强，应尽量避免。

Figure 8 Chaos diagram of the system complexity with the changes of parameters c and d图8 参数c、d同时变化时系统的复杂度混沌图

3 系统电路设计与仿真

为了验证该混沌系统的动态特性，本文利用Multisim软件对其电路进行设计与仿真。电路采用3554AM运算放大器和AD633乘法器实现，供电电压设为±15 V。为了便于该系统在实际电路中实施，对其进行时间尺度变换，令τ=100t得：

(7)

根据基尔霍夫电路定律，系统的电路状态方程表示如式(8)所示：

(8)

将式(8)与式(7)进行比较,令C1=C2=C3=10 nF，可以得到其电阻参数，R1=R2=50 kΩ,R3=100 kΩ,R4=10 kΩ,R6=90.9 kΩ,R7=71.4 kΩ,R11=100 kΩ,R5=R8=R9=10 kΩ,R10=R12=200 kΩ，电路原理如图9所示。根据所设计的电路和给定的元件参数进行Multisim仿真，在虚拟Tektronix示波器上可以观察到相图，如图10所示，电路实验结果与数值仿真结果相一致，证实系统是准确的。

4 混沌系统同步控制

混沌因其不可预测性和高度伪随机性在保密通信领域得到了广泛的应用[19,20]。利用混沌的时间复杂性和表面随机性，可以将要传输的信息隐藏在混沌信号中，然后在接收端采用混沌同步技术获取有用信息[21,22]。本文采用非线性反馈与线性反馈2种方法实现2个混沌系统的同步，并对线性反馈同步电路进行了仿真。响应系统具有与驱动系统相同的电路结构，但其初始值不同。随着时间的推移，2个相同的混沌系统可以在其状态变量之间实现并保持同步。

Figure 9 Circuit schematic图9 电路原理图

Figure 10 Circuit simulation experiment results图10 电路仿真实验结果

4.1 非线性反馈同步控制

设系统(1)为驱动系统，加入控制项后的响应系统数学模型如式(9)所示：

(9)

(10)

由此可将原同步问题转化为误差系统式(10)在原点(0，0，0)处的渐进稳定性问题。

定理1对于驱动系统(1)与响应系统(9)，若取系统的非线性控制律如式(11)所示:

(11)

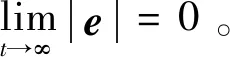
证明将控制律式(11)代入误差系统式(10)得:

(12)

构造如式(13)所示的Lyapunov函数:

(13)

将式(13)分别沿着误差向量e求导，并结合式(10)，得：

(14)

□

利用Matlab软件进行数值仿真，设驱动系统(1)的初始值为：x(0)=1，y(0)=2，z(0)=3，响应系统(9)的初始值为:x1(0)=4，y1(0)=5，z1(0)=6，控制器参数取k=-13，则该混沌系统同步时驱动和响应系统的状态变量随时间的变化情况与系统误差收敛曲线如图11所示。

Figure 11 Timing diagram and error curve of system synchronization图11 系统同步的时序图与误差曲线

仿真结果显示，所设计的非线性反馈控制律可以使驱动系统(1)与响应系统(9)达到同步。但是，上述所设计的非线性反馈控制器比较复杂，在电路实现方面较为不易，如何进一步简化控制律结构与优化系统同步方法就显得极为重要。由于线性反馈控制同步电路简单且在物理实现上较为容易，故下面采用线性反馈控制方法，通过系统的最大Lyapunov指数来确定控制参数的取值范围，从而达到该系统的同步控制，并对其设计电路仿真实验来验证此方法的可行性。

4.2 线性反馈同步控制

基于线性反馈同步方法，当选取系统参数a=20，b=14，c=11，d=5时，在式(1)上加入控制项后将其设为响应系统，其数学模型如式(15)所示：

(15)

其中k为线性控制参数。令e1=x1-x，e2=y1-y，e3=z1-z，则误差系统方程可由式(15)减去式(1)得到,如式(16)所示：

(16)

设驱动系统的初始值为：x(0)=1,y(0)=1,z(0)=1，响应系统的初始值为：x1(0)=10,y1(0)=10,z1(0)=10，取步长T=0.01，由数值计算可得，系统的最大Lyapunov指数LEmax=2.487≈2.5。根据线性反馈同步控制机理[23,24]，当取控制参数k>LEmax时，采用线性反馈控制方法，可以使混沌系统达到同步。控制参数k取不同值时的同步误差曲线和时域波形如图12所示。

Figure 12 Numerical simulation of system synchronization图12 系统同步数值仿真

由数值仿真结果可得，当k=2时，驱动系统与响应系统不同步；当k=2.5时，驱动系统与响应系统经过一段时间后最终达到同步；当k=3.5时，驱动系统与响应系统经过短暂时间后达到同步。由上述可得，当k大于系统最大Lyapunov指数时，误差曲线最终收敛于0，时域波形也达到同步，并且当k越大时，达到同步所需要的时间越短。相比文献[6]中的耦合同步，根据最大Lyapunov指数能够更精确地控制混沌系统同步。

为了验证上述理论分析与数值仿真的正确性，在Multisim软件上对其进行同步电路仿真实验，由图9可得，C4=C5=C6=10 nF,R14=90.9 kΩ,R15=71.4 kΩ,R19=50 kΩ,R20=50 kΩ,R21=100 kΩ,R22=200 kΩ,R23=100 kΩ,R24=200 kΩ。同步电路原理如图13所示。相比文献[23]中的同步控制电路，此控制电路减少了一组反相比例放大电路，使得电路更加简单、易实现。

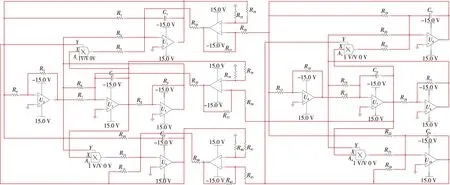
Figure 13 Simulated circuit diagram of synchronous circuit图13 同步电路仿真电路图

当R29=R39=R44=500 kΩ时，k=2；当R29=R39=R44=400 kΩ时，k=2.5；当R29=R39=R44=285 kΩ时，k=3.5。当k取不同值时，相应的状态变量的相图如图14所示，同步时x1-x2的时域波形相重合，并且其相图为一条通过原点的直线。而且随着k值的增大，2个混沌系统达到同步时所用到的时间越少，由此可见电路实验结果与数值仿真结果一致，证明了此方法的可行性。

Figure 14 Simulation results of chaotic synchronization circuit图14 x1与x2同步仿真实验相图

5 结束语

本文根据Bao系统的构建模式，提出一个新的三维混沌系统。对新系统的吸引子相图、Poincare截面、0-1测试以及Lyapunov指数谱与分岔图等基本动力学特性进行了研究分析，结果表明该系统具有新的拓扑结构和更为复杂无序的混沌特性。此外，通过计算谱熵(SE)复杂度与C0复杂度，为电路参数的选取提供了一种直观有效的方法。利用Multisim软件设计实现了该系统电路，仿真结果证实了理论分析与数值仿真的正确性。最后，采用非线性反馈与线性反馈控制方法实现了该混沌系统的同步，给出了系统线性同步控制参数的范围，使得同步控制更加精确与严谨，并通过数值仿真与电路实验证实了此方法的有效性。但是，该方法在保密通信领域中的应用还有待进一步研究，并且其硬件电路还有待实现。