有源磁控忆阻超混沌电路实现及图像加密*

张 洁,徐龙昊,尹宝全

(1.西北师范大学物理与电子工程学院，甘肃 兰州 730070；2.甘肃省智能信息技术与应用工程研究中心，甘肃 兰州 730070)

1 引言

1971年，Chua教授[1]提出了忆阻器理论。近年来，基于忆阻器的混沌系统设计已经成为忆阻器研究的热点之一[2 - 5]。Chen等[6]利用一种新型的余弦忆阻器构造了一个四维忆阻系统。孙亮等[7]将局部有源忆阻器用于模拟生物突触，构建了一个局部有源忆阻突触耦合HR(Hindmarsh Rose)神经元网络。王匀等[8]利用忆阻器结合分数阶理论和时滞系统理论，提出了一种基于分数阶时滞的非线性混沌电路。Li等[9]在三维系统中引入忆阻器，得到了一个四维超混沌系统，其具有无限个稳定和不稳定的平衡点。虽然对忆阻器的研究开展得较多，但基于忆阻器的超混沌系统的研究却相对较少。

此外，混沌系统由于其随机性，被广泛应用于图像加密中。Liu等[10]提出了基于分段线性混沌系统加密的图像加密算法。高成明等[11]提出了一种基于混沌的置乱-扩散图像加密算法。方鹏飞等[12]提出了一种基于改进的二维Logistic混沌映射与DNA序列运算相结合的分组图像加密算法。上述研究虽然都很好地完成了图像加密，但都是单次加密。在图像加密的过程中多次加密往往比单次加密的效果要好。

本文首先在Rucklidge[13]提出的三维系统的基础上，加入二次非线性有源磁控忆阻器，构造了一个四阶超混沌系统；然后通过相图、Lyapunov指数谱、分岔图和平衡点等指标，对该系统的动力学行为进行分析，并基于Multisim电路仿真软件和现场可编程门阵列FPGA(Field Programmable Gate Array)数字硬件电路设计实现了电路；最后结合DNA加密设计了一种新的图像加密算法，同时对加密后的图像进行分析。结果表明，本文提出的混沌系统应用于图像加密具有较高的安全性能。

2 新四阶超混沌系统

Rucklidge[13]提出的三维系统的方程如式(1)所示：

(1)

其中，α、β和p均为常数，α=2,β=6,p=-1;x、y和z均为状态变量，并且系统有3个平衡点。现考虑引入一个忆阻器到这个三维系统。这里选用二次非线性磁控忆阻器,忆阻器的函数表达式如式(2)所示：

W(φ)=-m+n|φ|

(2)

其中,m=1,n=4。将流经忆阻器的磁通表示为第4个状态变量，状态变量y为忆阻器两端的电压，忆阻强度用g(g>0)表示，引入后的系统方程如式(3)所示：

(3)

其中,α=2,β=6,g=0.1,p=-1;x、y、z和u均为状态变量。当系统的初始值为(0.1,0.1,0，0)时，式(3)存在复杂的超混沌现象。利用四阶龙格库塔算法求解式(3)，步长设置为0.1，结果如图1所示。图1展示了式(3)混沌吸引子在(x,y),(y,z)，(x,z)和(y,u)4个平面的二维映射图。观察图1可以发现，相图有2个涡卷和复杂的拉伸结构，并且图1b和图1c是左右对称的图形。

Figure 1 Phase diagram of hyperchaotic system图1 超混沌系统的相图

3 超混沌系统的动力学分析

3.1 系统平衡点

为求系统平衡点，令超混沌系统方程式(3)的右边等于零，得到式(4):

(4)

当系统方程的参数为α=2,β=6,g=0.1,p=-1时，系统的平衡点为(0,0,0,ε),ε为任意数，并且可以得到式(4)的Jacobi矩阵如式(5)所示：

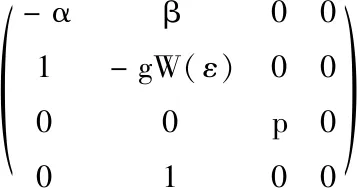
(5)

式(5)的特征方程如式(6)所示：

F(λ)=λ(λ-p){(α+λ)[gW(ε)+λ]-β}=0

(6)

3.2 系统的对称性和耗散性

系统对坐标变换 (x，y，z，u)→(-x，-y，z，-u)具有不变性，所以系统关于z轴对称。通过式(3)得到系统的散度如式(7)所示：

(7)

即▽V=-3.1-0.4|φ|，其中|φ|≥0。所以散度小于0，系统具有耗散性，且系统以指数形式dV/dt=e(-3.1-0.4|φ|)t收敛,其中V表示存储在系统中的能量，t表示时间，此式表明系统的能量在不断地减少。当t→∞时所有的系统轨迹最终都将会被限制在一个体积为0的极限点集上，而且它的动力学行为将会被固定在一个吸引子上，这充分证明了吸引子的存在。

3.3 系统的Lyapunov指数分析

Lyapunov数值描述了相空间相邻轨道平均指数散度的数值特征，又称Lyapunov指数，是一种用来识别混沌运动的数字特征。当系统参数设定为α=2,β=6,g=0.1,p=-1时，计算系统的Lyapunov指数，即LE1=0.3896,LE2=0.02659,LE3=-0.4065,LE4=-4.012。系统的Lyapunov指数之和是负数，且有2个Lyapunov指数大于0。计算系统的LE维数DL如式(8)所示：

(8)

可以得到系统的LE维数为分数维且大于3，故系统是超混沌系统。

3.4 系统的Poincare截面图和功率谱图

Poincare截面也是系统动力学行为特征的一个重要判据。当Poincare截面上只有1个不动点或少数离散点时，运动是周期的；当Poincare截面上是1条封闭的连续曲线时，运动是拟周期的；当Poincare截面上是一段连续曲线或是一些成片的密集点时，运动是混沌的。从图2可以明显看出，Poincare截面上的点呈现为连续曲线或片状的密集点，所以该系统是混沌的。

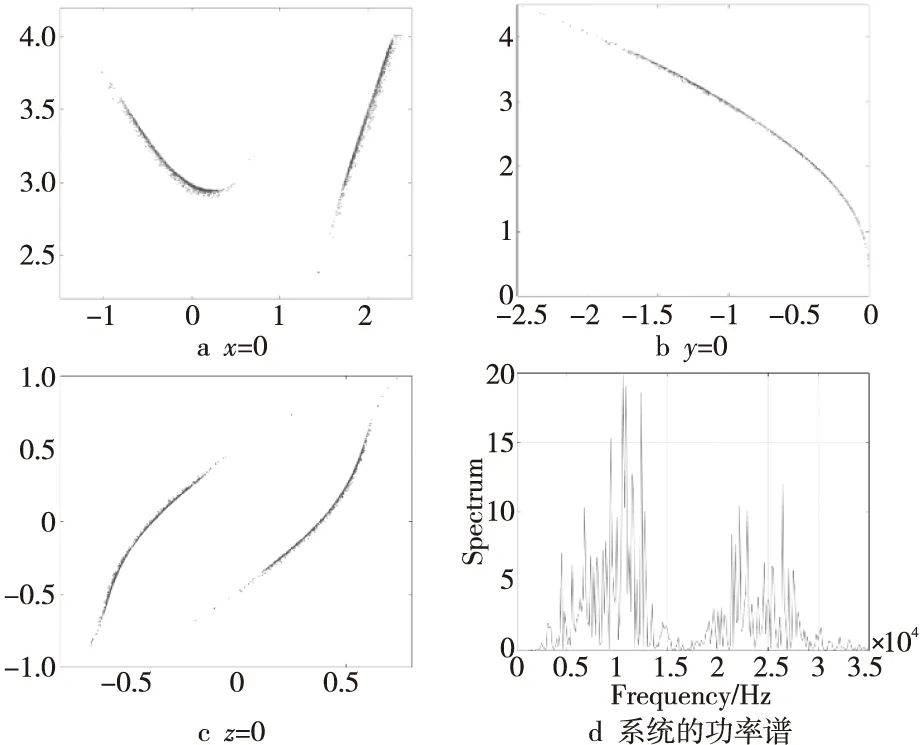
Figure 2 Cross section and power spectrum of Poincare 图2 Poincare截面图和功率谱

对于混沌系统来讲，若产生的混沌信号是非周期信号，则其系统的功率谱也是非周期的连续谱。图2d是本文系统的功率谱，该功率谱连续表明系统处于非周期状态，峰值的出现代表系统中有分岔现象发生。

3.5 系统的分岔图及参数分析

分岔是指系统的动力学运动状态随着系统参数或者状态变量初始值的改变而发生变化的一种现象。系统的运动状态可以由一种稳定状态变为另一种稳定状态，准周期状态到混沌状态，一种混沌到另一种混沌等。随着系统参数取值的改变，系统的Lyapunov指数谱和分岔图也发生改变。

当α=2,β=6,g=0.1时，使参数p在(-2,0)内变化，如图3所示。从图3中可以看出，Lyapunov指数谱和分岔图具有很好的一致性。当p∈[-1.9,-1.83],[-1.71,-1.61]或[-0.19,0]时，系统处于周期状态，如图4a所示；当p∈[-1.61,-1.5],[-1.43,-0.95],[-0.66,-0.48]或[-0.34,-0.19]时，系统处于混沌振荡状态，如图4b所示；当p∈[-1.5,-1.43],[-0.95,-0.66]或[-0.48,-0.34]时，系统处于超混沌状态,如图4c和图4d所示。

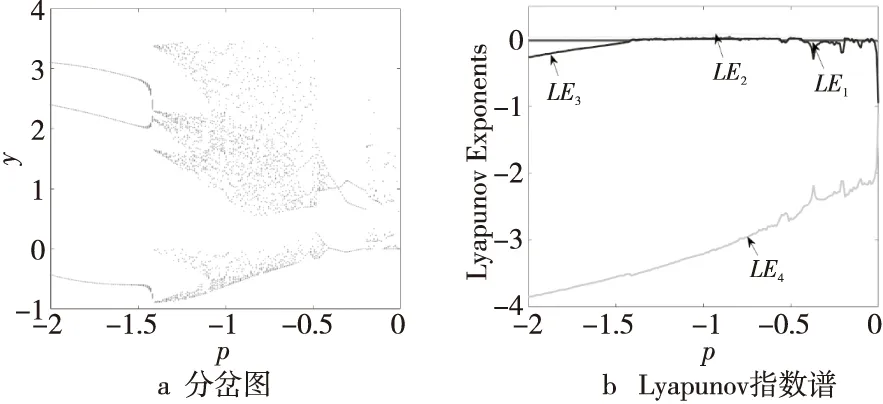
Figure 3 Bifurcation diagram and Lyapunov exponential spectrum varying with parameter p图3 随参数p变化的分岔图和Lyapunov指数谱

Figure 4 Phase diagrams varying with parameter p图4 随参数p变化的相图

当α=2,β=6,p=-1时，使参数g在(-1,1)内变化。图5是随g变化的Lyapunov指数谱和分岔图。当g∈[0.61,0.63]时，系统处于拟周期轨道状态，如图6a所示；当g∈[0.63,1]时，系统处于周期轨道状态,如图6b所示；当g∈[-1,-0.69],[-0.53,-0.49]或[0.54,0.61]时，系统处于混沌轨道状态,如图6c所示；当g∈[-0.69,-0.53]或[-0.49,0.54]时，系统处于超混沌轨道状态，如图6d所示。

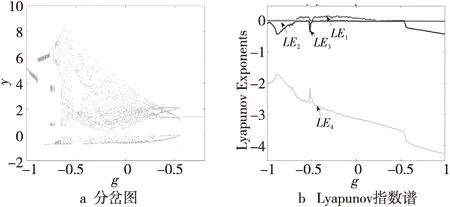
Figure 5 Bifurcation diagram and Lyapunov exponential spectrum varying with parameter g图5 随参数 g变化的分岔图和Lyapunov指数谱

Figure 6 Phase diagrams varying with parameter g图6 随参数g变化的相图

3.6 系统的共存吸引子分析

为了更好地对新超混沌系统的状态进行研究和分析，本文通过改变系统的参数，发现系统存在不同种类的吸引子，图7是参数g变化时比较典型的3个系统吸引子相图,图7a为周期吸引子共存，图7b为混沌吸引子共存，图7c为超混沌吸引子共存。其中，在u=0的上半部分实线初始值为(-0.1,-0.1,0,0)，下半部分虚线的初始值为(0.1,0.1,0,0),观察上图可以看出本文系统在不同初始值下存在对称的吸引子。

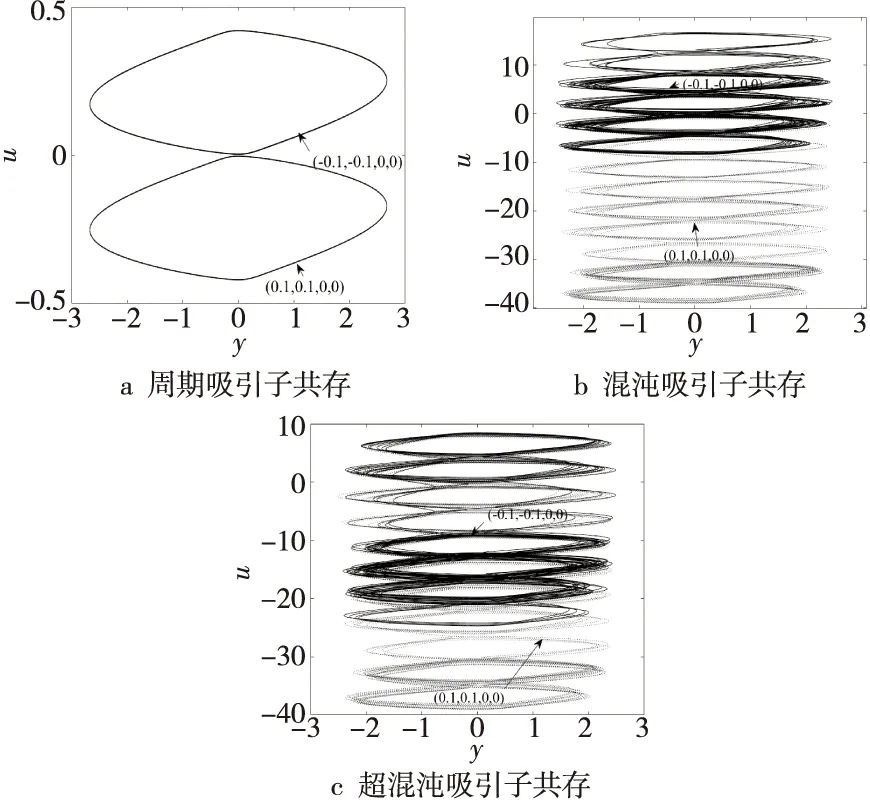
Figure 7 Attractor coexistence diagrams of the system图7 系统的吸引子共存相图

4 电路设计仿真及FPGA实现

4.1 系统的电路设计

图8b是非线性有源磁控忆阻等效实现电路的原理图，图中的虚线部分为绝对值函数电路(即图8a中的H(·))。通过计算得到的忆阻器等效电路表达式如式(9)所示：

W(φ)=-m+n|φ|=

(9)

其中，Rh和Rsat为忆阻器电路的电阻，方便在仿真软件中和系统整体电路的电阻进行区分。

整体电路设计时，首先对系统方程式(3)作比例压缩变换，设RX→X,RY→Y,RZ→Z,Ru→U,其中R为变量比例压缩因子。设R=0.5，变换后的方程如式(10)所示：

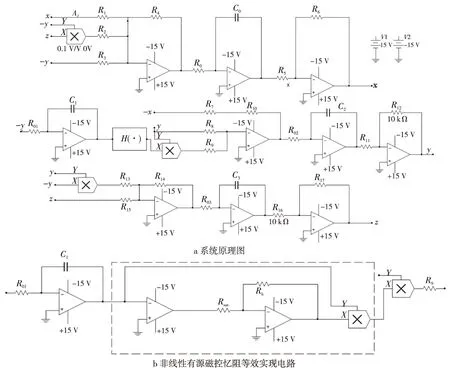
Figure 8 System circuit diagram 图8 系统电路图

(10)

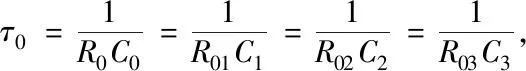
(11)

系统电路原理图如图8所示。

对比式(10)和式(11)，得到R0=R01=R02=R03=50 kΩ,C0=C1=C2=C3=33 nF,R5=R6=R7=R10=R11=R12=R16=R17=10 kΩ,R1=50 kΩ,R2=R13=5 kΩ,R3=16.7 kΩ,R9=83.3 kΩ,R4=R8=R14=R15=100 kΩ,Rsat=13.5 kΩ,Rh=6.05 kΩ。

通过在Multisim电路仿真软件上进行验证，实际相位图如图9所示，与上述的理论相位图一致。因此验证了该超混沌系统存在吸引子。

Figure 9 Diagram of circuit simulation 图9 电路仿真图

4.2 FPGA数字硬件电路实现

模拟器件容易受到许多环境因素的影响，从而造成混沌系统不稳定。因此，基于现场可编程门阵列(FPGA)的数字电路因具有较高的并行计算能力和能被应用于生物医学工程领域而受到人们的青睐。

本文通过采用Euler 算法对系统方程进行离散化处理，离散后的方程如式(12)所示,通过XILINX的 FPGA开发软件Vivado 进行设计,系统方程中的实数处理采用定点小数与截位计算相结合的方式。采样的时间步长ΔT设定为0.001,图10为示波器上得到的波形，观察发现与Multisim和Matlab软件的仿真结果一致。

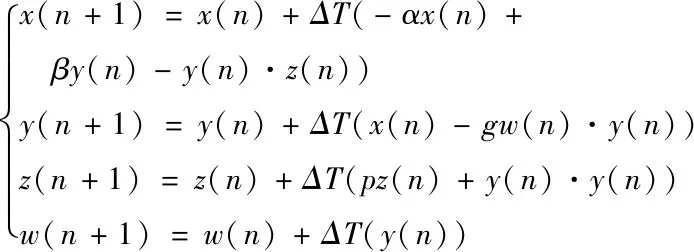
(12)

Figure 10 FPGA-based object map图10 基于FPGA的实物图

5 图像加密

5.1 加密算法

混沌系统由于其不确定性和初始条件的高敏感性，被广泛应用到图像加密中。传统的加密通常是一次加密，这种加密往往容易遭受攻击导致信息泄露，因此需要新的混沌系统配合新的加密算法来完成加密。本文采用置乱-扩散与DNA加密相结合的双重加密算法，达到了更好的加密效果。具体加密流程如图11所示，解密过程为加密过程的逆运算。

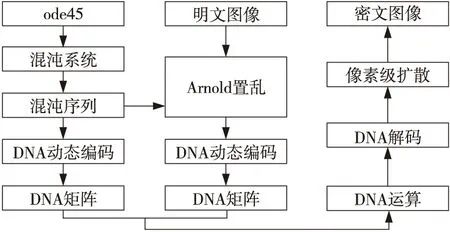
Figure 11 Flow chart of encryption 图11 加密流程图

5.1.1 混沌序列

利用ode45算法计算混沌系统的初始值得到4个混沌序列，记为xi、yi、zi和ui，i=1,2,…,M×N。为了抵御明文攻击，提高对明文的敏感性，对混沌序列进行如式(13)所示的处理:

(13)

其中,xi、yi、zi和ui(i=1,2,…,M×N)为明文参与前的初始序列；x′i、y′i、z′i和u′i(i=1,2,…,M×N)为明文参与后的混沌序列；Pi(i=1,2,…,M×N)为明文图像的像素值。

然后迭代混沌系统，本文为了获得更好的随机性，舍弃了前面的2 000项。

5.1.2 Arnold置乱

Arnold置乱变换是由Arnold提出的一种置乱方法，其实质是新旧位置的一一映射，具体变换公式如式(14)所示：

X=(x+by) modN

Y=[bx+(ab+1)y] modN

(14)

其中，a、b是Arnold置乱的2个参数，a=x′i，b=y′i(i=1,2,…,M×N);(X，Y)为坐标 (x，y)处的像素被置乱后的位置，通过Arnold置乱得到置乱矩阵A。

5.1.3 DNA动态编码

众所周知，一个DNA序列包含腺嘌呤(A)、胞嘧啶(C)、鸟嘌呤(G)和胸腺嘧啶(T)4种核酸碱基。其中，A和T互补，C和G互补。计算机系统中的信息用二进制数字0和1表示。因为二进制中的0和1是互补的，所以00和11、01和10也分别是互补的。因此，本文利用DNA序列中的A、C、G和T分别替换二进制序列中的00、01、10和11。本文中的DNA加密算法通过混沌系统产生的z′i(i=1,2,…,M×N)混沌序列转化为0～255之间的整数，再转换为矩阵，记为矩阵B;然后将矩阵B和Arnold置乱得到的矩阵A转化为二进制矩阵，再根据相应的DNA编码规则，把二进制矩阵中的每两个二进制数字转换为一个DNA碱基，从而得到对应的DNA序列矩阵，把最后经过DNA计算的矩阵记为C。解码是编码的逆过程。完整的DNA编码规则如表1～表4所示。

Table 1 Coding and decoding rules of DNA表1 DNA编码和解码规则

5.1.4 像素级扩散

首先根据DNA解码规则，对矩阵C进行动态解码，得到二进制矩阵，并将其转化为十进制矩阵，记为Fi，伪随机序列u′i即为Di,Li为扩散后的序列。然后开始进行扩散，扩散采用异或运算的双向扩散处理，即正向扩散和逆向扩散各一次。正向(按i从1到M×N)的算法与其逆运算如式(15)所示：

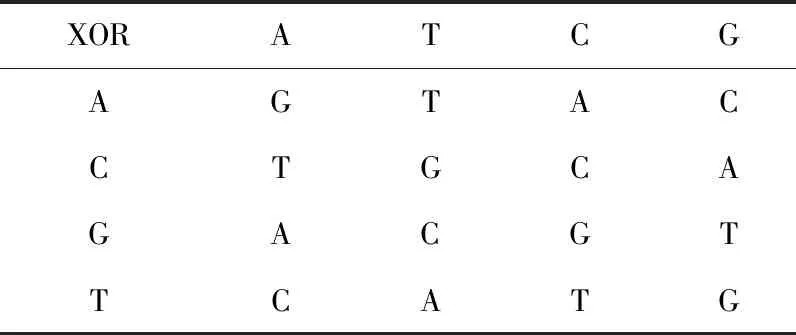
Table 2 XOR operation rules of DNA sequence表2 DNA序列的异或运算规则

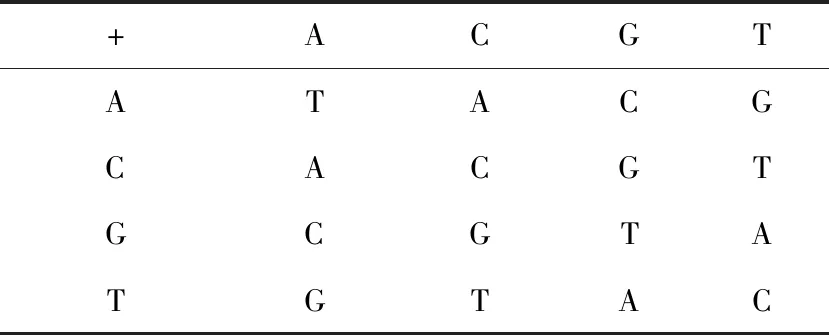
Table 3 Addition operation rules of DNA sequence 表3 DNA序列的加法运算规则

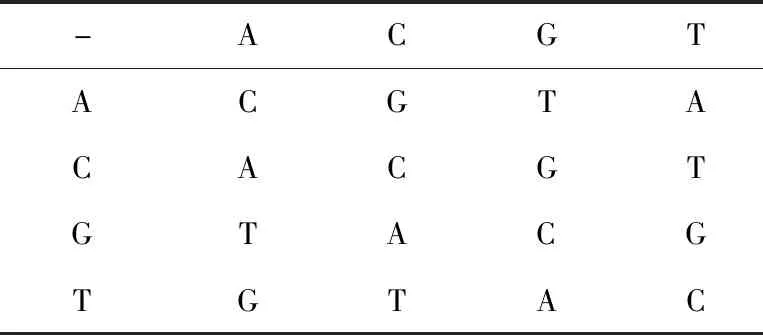
Table 4 Subtraction operation rules of DNA sequence 表4 DNA序列的减法运算规则

(15)

逆向(按i从1到M×N)的算法与其逆运算如式 (16)所示：

(16)

本文在图像加密的实验中选用了标准的256×256的Lena图像，加密后的结果如图12所示，观察发现密文图像已没有任何原图的图像特征。

Figure 12 Encryption effect of image图12 图像加密效果

5.2 图像的安全性能分析

5.2.1 密钥空间及敏感性分析

密钥空间是指所有合法密钥构成的集合，当密钥空间足够大时，穷举攻击可以被有效地对抗。一般规定当密钥空间大于2100时，加密系统的安全可靠性就会得到保障[14]。本文密钥参数为(X0,Y0,Z0,U0)，计算得到的密钥空间大小为2×1060,远远大于上述要求。

在保持其中3个不变的前提下，Y0变为Y0+10-16时，对其进行解密，可以解密出原始图像；但是当Y0变为Y0+10-15，记为Y′0时，对其进行解密，无法解密出原始图像。同理,当U0变为U0+10-15，记为U′0时，对其进行解密，也无法解密出原始图像。结果如图13所示，对其余密钥参数测试时，也会出现类似的结果。这说明本文图像加密算法具有良好的密钥敏感性。

Figure 13 Images decrypted with the wrong key and the right key respectively图13 分别使用错误密钥和正确密钥解密的图像

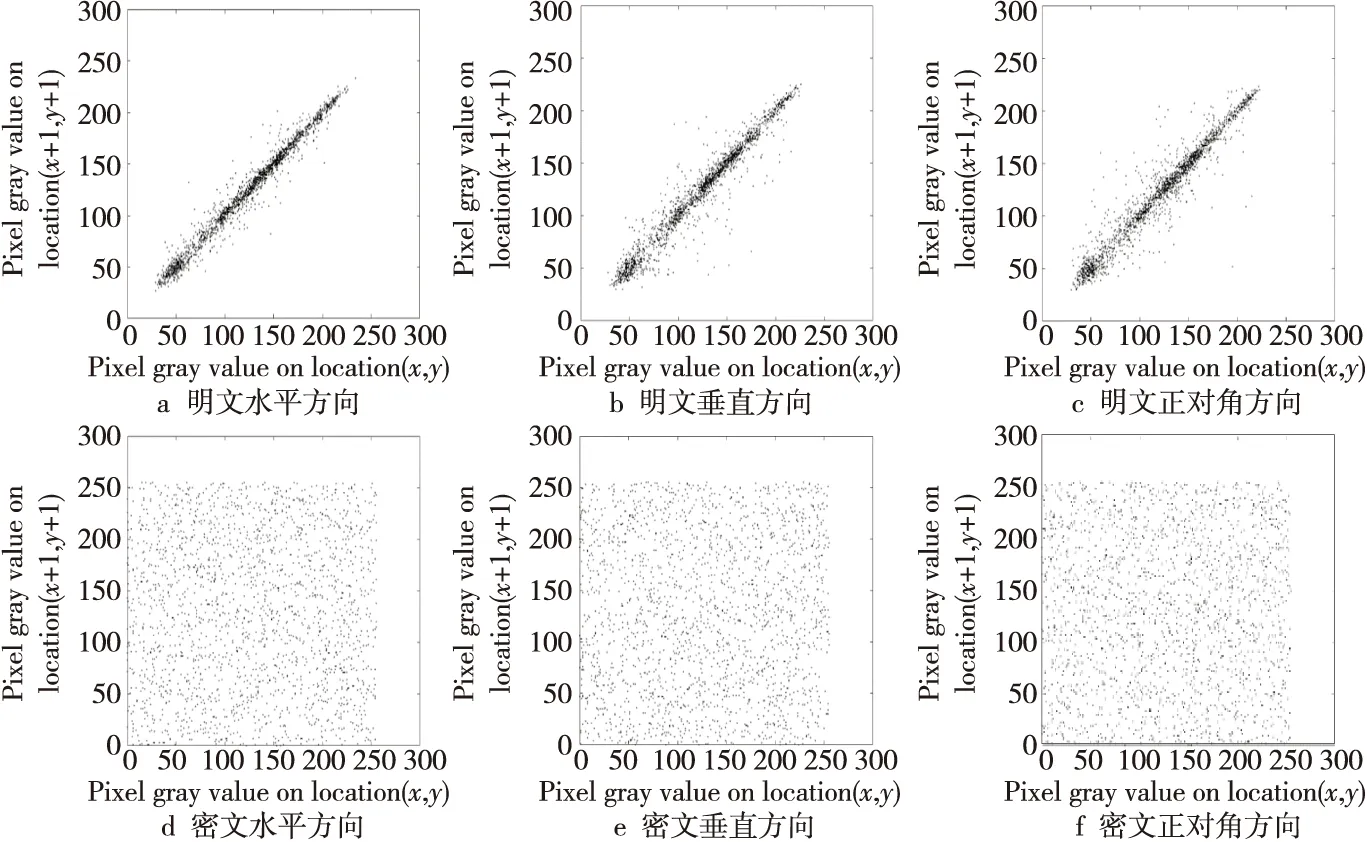
Figure 14 Correlation coefficient of image图14 图像的相关系数

5.2.2 相关系数计算及分析

图像之间的相关特性也是衡量图像加密效果的一个重要因素。一般地，明文图像在水平、垂直和对角方向上的相邻像素点间均具有较强的相关性，而密文图像中的相邻像素点间应没有相关性。相关性计算如式(17)所示：

(17)

其中，u,v表示任意相邻的2个像素点值，E(u)和D(u)分别表示期望和方差。本文选取上面加密前后的Lena图像用于计算相关系数，得到加密前后图像的相关系数图，如图14所示。计算加密前后图像在水平、垂直和正对角3个方向上的相关系数，结果如表5所示。

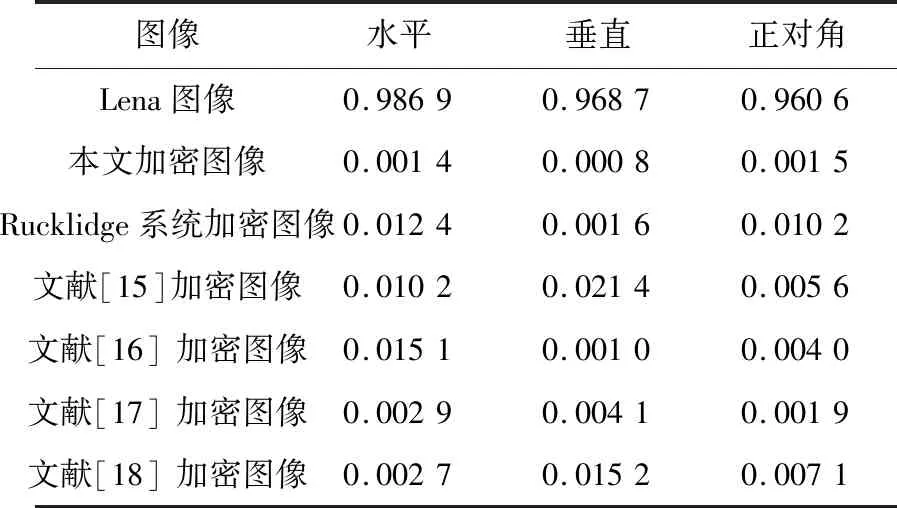
Table 5 Comparison of correlation coefficients表5 相关系数对比

由表5可知，明文图像在3个方向上的相关性很强，接近于1，而对应密文图像的像素则均匀分布，其相关系数接近于0。利用原始Rucklidge[13]的三维系统产生3个混沌序列,分别为xi、yi和zp，其中前2个序列的长度为i=1,2,…,M×N，序列zp的长度加倍，即p=1,2,…,2×M×N。然后将序列zp分为2个小序列ri和ti，长度分别为i=1,2,…,M×N。将4个序列分别应用于本文的图像加密算法。将本文新系统的加密图像和其它文献加密图像进行对比，发现本文系统加密图像各个方向的相关系数都要强于它们。因此，新系统算法的加密效果非常明显。

5.2.3 鲁棒性分析

衡量一个加密算法抗干扰能力最重要的标准是鲁棒性。本文选择Lena图像进行实验分析，利用噪声攻击和剪切攻击来测试本文算法的鲁棒性。对加密图像施加0.05倍的椒盐噪声，解密图像如图15b所示。剪切1/4的加密图像的解密结果如图15d所示。对比实验结果发现，利用本文加密算法仍能恢复出大部分原始图像的信息。这表明本文算法可以在一定程度上抵抗噪声攻击和剪切攻击，具有较好的鲁棒性。

Figure 15 Robustness analysis of image图15 图像的鲁棒性分析

5.2.4 信息熵

信息熵能够反映图像的不确定性，一般认为，熵越大则信息量越大，可视信息反而越少。信息熵的计算如式(18)所示[14]：

(18)

其中，2n表示图像中像素值的所有状态数，p(si)表示该像素值在整幅图像中所占的概率。可以得到具有2n个状态的信息，信息熵就是n。因此一幅标准的具有 256 个状态的图像，理想的信息熵应该是 8。本文系统加密后的图像信息熵为7.998 9,与理论值8非常接近。表6给出了其它系统加密图像的信息熵，与本文的信息熵对比后，发现本文新系统的加密效果良好。

Table 6 Comparison of information entropy 表6 信息熵对比

6 结束语

本文设计了一个四阶超混沌电路系统，并分析了系统的相图、Lyapunov指数谱、Poincare截面图和分岔图以及系统的稳定性和耗散性，证明了系统的混沌特性，还设计出了系统的电路，并在Multisim电路仿真软件和FPGA数字硬件电路实现中得到了验证；最后将新混沌系统与DNA加密算法相结合，设计出了新的图像加密算法，并分析了加密图像的安全性能，发现其具有良好的加密效果，可以被广泛应用到图像加密领域。