基于观测器的马尔科夫跳变系统的滑模控制问题
2022-08-19胡显伟
胡显伟
(沈阳市艺术幼儿师范学校,辽宁 沈阳 110015)
由于Markov跳变系统具有广泛的适用性和简单的数学描述,使其在控制领域得到了越来越多的关注[1-2]。而半Markov 跳变系统比Markov 跳变系统有更加广泛的实际应用,如航空航天系统、网络系统和电力控制系统等[3-6],这使得半Markov 跳变系统逐渐成为当前的研究热点,并出现了许多重要的理论成果[7-8]。
在现实世界的系统中存在时滞,时滞存在于观测的信号、控制输入和系统的状态等系统的各个部分。时滞分为两种:不变时滞和时变时滞。时变时滞的应用更加广泛,并且有更低的保守性,使得关于时变时滞的研究得到了广大学者的关注[9-11]。
滑模控制在鲁棒控制方法中起着举足轻重的作用,是非常高效的非线性控制方式,具有控制结构简单、反应迅速等优点。滑模控制方式的原理:首先设计了一种理想的滑模面,然后设计一种理想的控制器使系统状态在有限的时间内到达滑模面上。基于滑模控制,文献[12]考虑了半Markov 跳变模糊系统的稳定问题,文献[13]研究了Markov跳变中立系统。
针对基于滑模观测器的Markov跳变系统的混合H∞和无源控制问题,本文设计了1 个观测器来测量1 个未知系统的状态,设计的反馈控制器和滑模面可以使闭环系统渐进稳定并且满足混合H∞和无源的性能指标。最终通过仿真,证明了所提理论的优越性和合理性。
1 问题描述
考虑以下带有外部干扰的非线性系统:
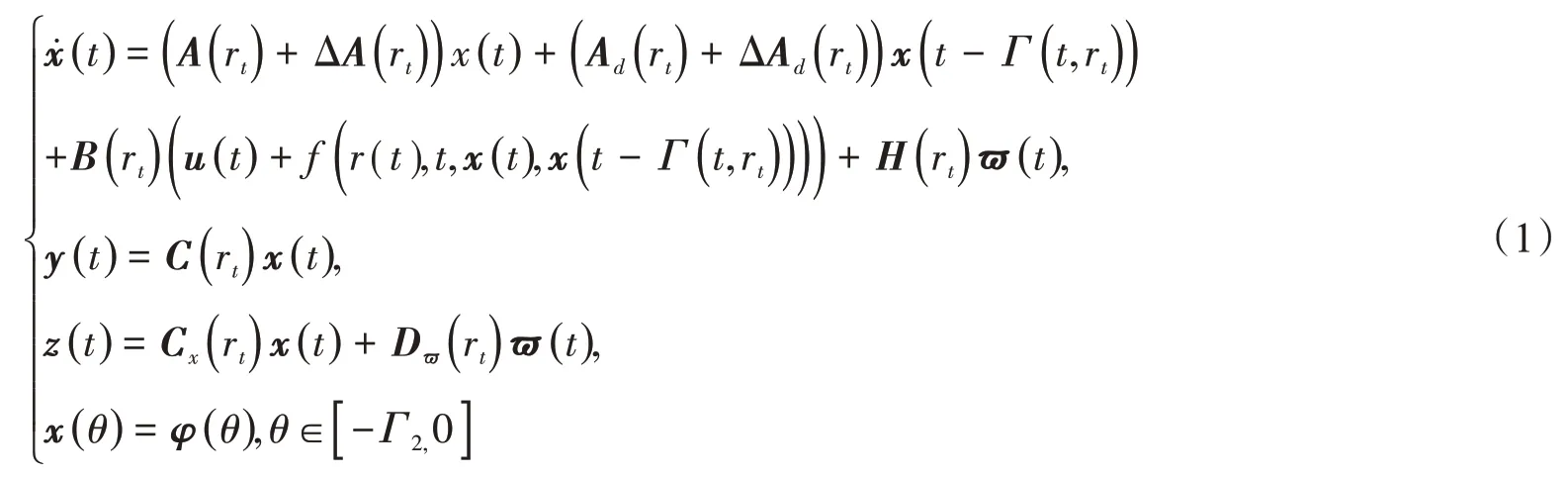
式中,x(t)∈Rn、u(t)∈Rm、ϖ(t)∈Rq、y(t)∈Rp和z(t)∈Rq分别是系统状态、控制器、外部扰动、系统输出和控制输出;f(r(t),t,x(t),x(t-Γ(t,rt)))∈Rm是连续的非线性函数;Γ2为时变时滞的上界;φ(θ)是初值,θ∈[-Γ2,0];为了方便计算,Λ(rt=i)用矩阵Λi来表示,i∈S;Ai、Adi、Bi、Hi、Cxi、Ci、Dϖi分别为常数矩阵;未知项ΔAi和ΔAdi范数有界。Mi、Ni、Ndi为常数矩阵;Ξ(i,t)满足Ξ(i,t)TΞ(i,t)≤I,∀i∈S且[ΔAiΔAdi]=MiΞ(i,t)[Ni Ndi]成立,其中{rt,t≥0} 是Markov过程。
在集合S={1,2,…,s} 中,概率矩阵为

假设1 非线性函数f(r(t),t,x(t),x(t-Γi(t)))满足
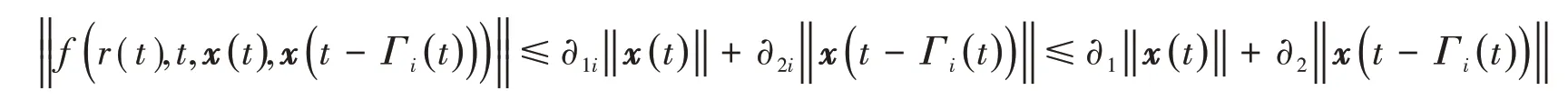
式中,∂1=max{∂1i};∂2=max{∂2i};∂1i和∂2i为非负常数。
假设2 时变时滞满足Γ1i(t)≤Γi(t)≤Γ2i(t),≤μi≤1,μi(i=1,2)是已知的常数。
引理1 矩阵D和E具有合适的维数,当ε>0、0<P∈Rn×n、Γ(t)TΓ(t)≤I时,下面不等式成立:
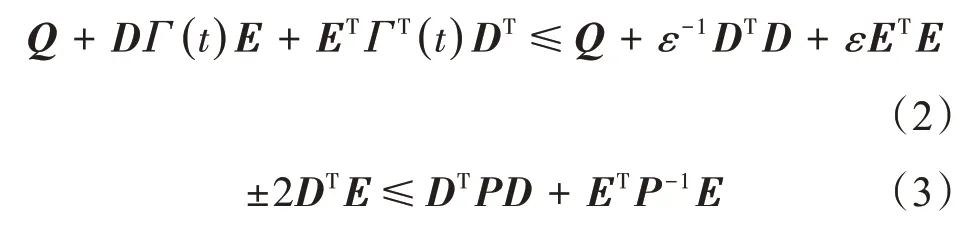
引理2 常数∂<β,矩阵M>0,向量x:[∂,β]→Rn,则下式成立:
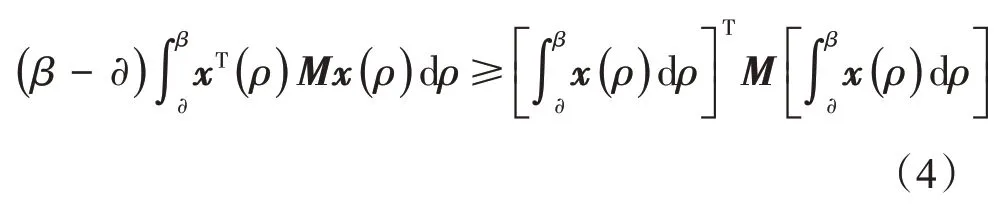
若矩阵Q>0,向量函数x:[∂,β]→Rn,则:
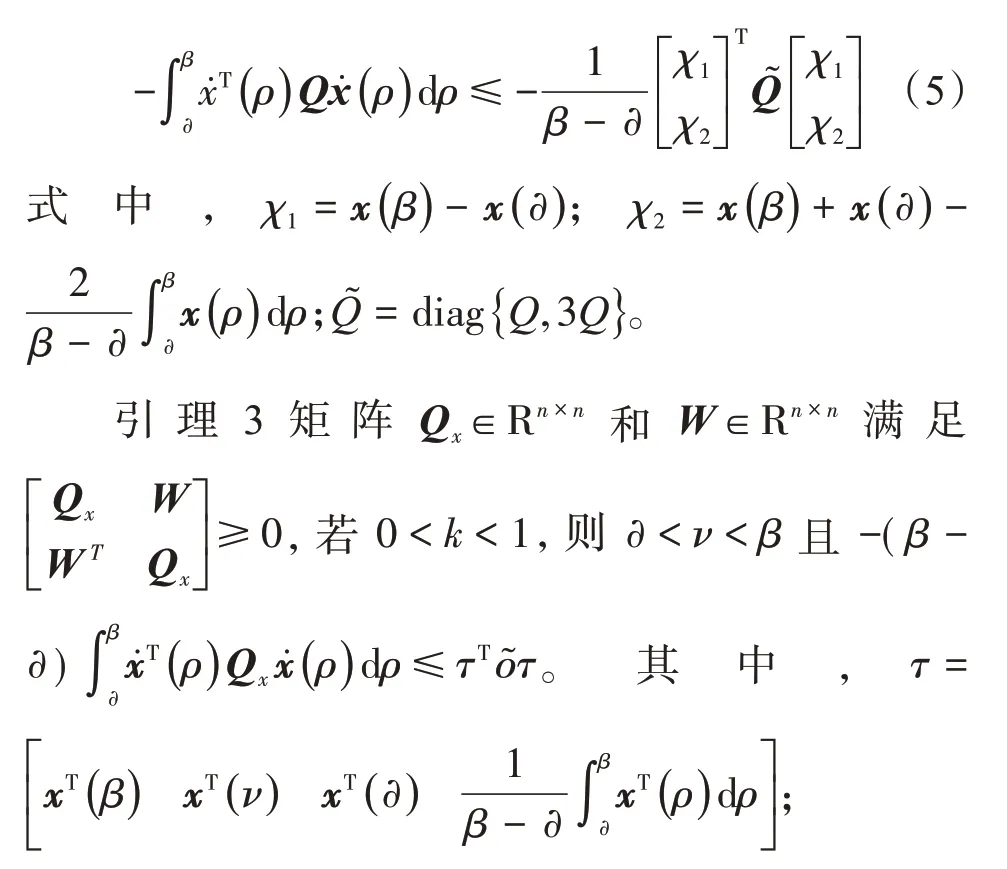
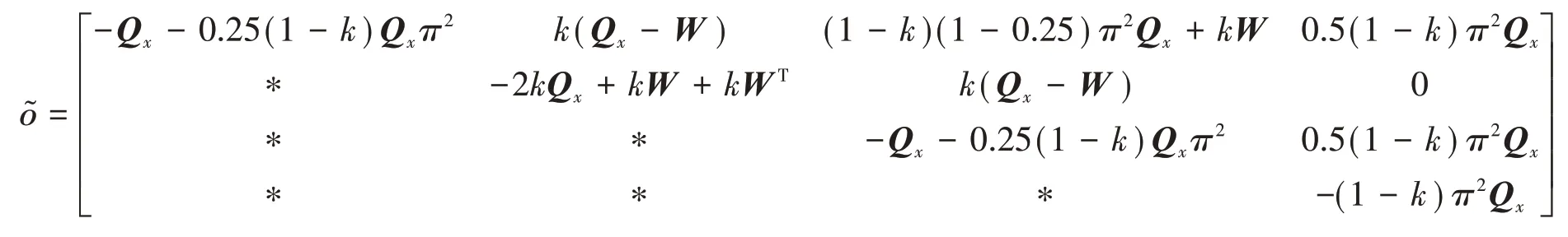
定义1 对于Tp≥0 和非零ϖ(t)∈L2[0,∞),γ(γ>0)是混合H∞与无源的性能指标。当初值为0时,下式成立:
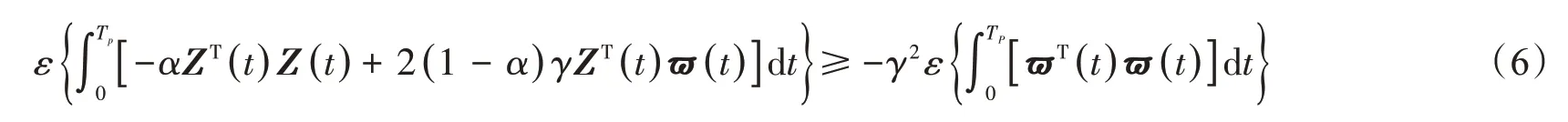
备注2:当性能指标α=1 时,称为H∞性能指标;当性能指标α=0 时,称为无源性能指标;当性能指标α∈(0,1)时,称为混合H∞和无源性能指标。
2 主要结果
考虑一个合适的观测器来估计非线性系统的未知状态,该观测器为
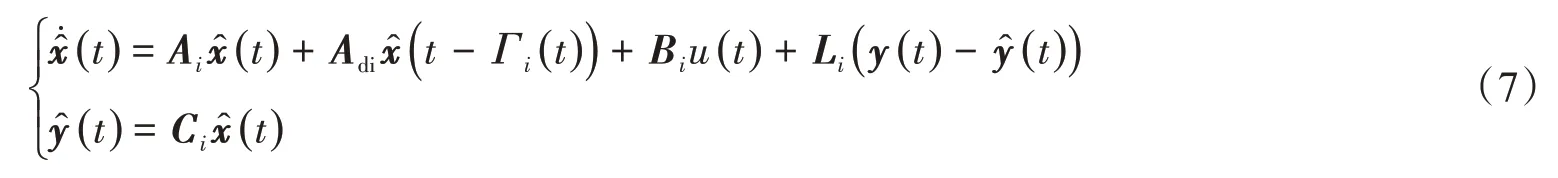
令e(t)=x(t)-,e(t)代表测量误差,则:
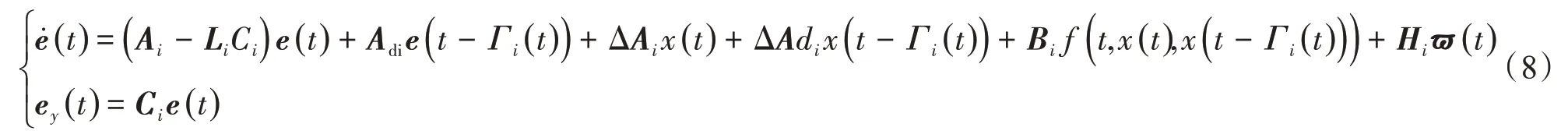
式中,ey(t)表示测量的输出误差。
2.1 积分滑模面设计
设计一类积分滑模面:
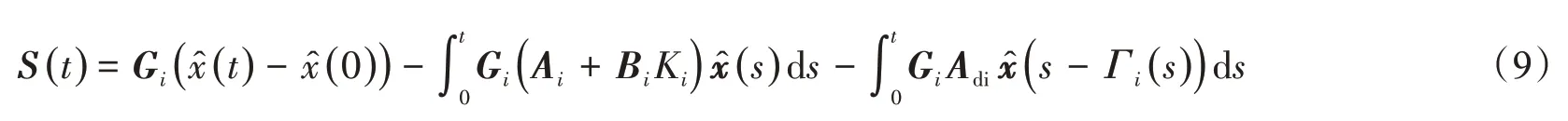
式中,Ki是控制器增益;是观测器初值;当S(t)=0 和=0 时,状态估计能够到达滑模面。因此,可得等效控制器Ueq(t)=-(GiBi)-1GiLiCie(t)。
将Ueq(t)带入式(7),可得动态滑模方程:
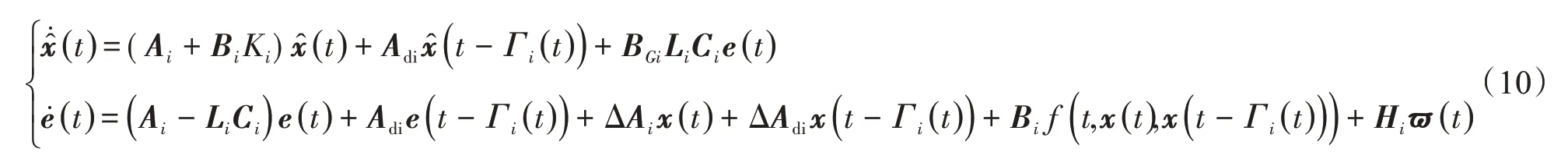
式中,BGi=I-Bi(GiBi)-1Gi。
2.2 稳定性分析
定理1 对于常数γ>0,0<Γ1<Γ2,0<k<1,0<μi<1,其中i=1,2。如果存在对称正定矩阵Pi、Si、Q1、Q2、Q3、Q4、Q5、Q7、Q8和参数ε1i、ε2i、ε3i、ε4i,∀i∈S,使得下列不等式成立:
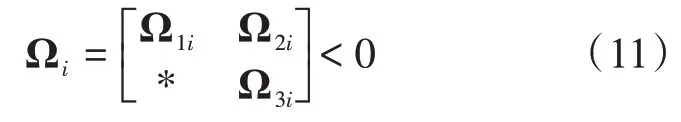
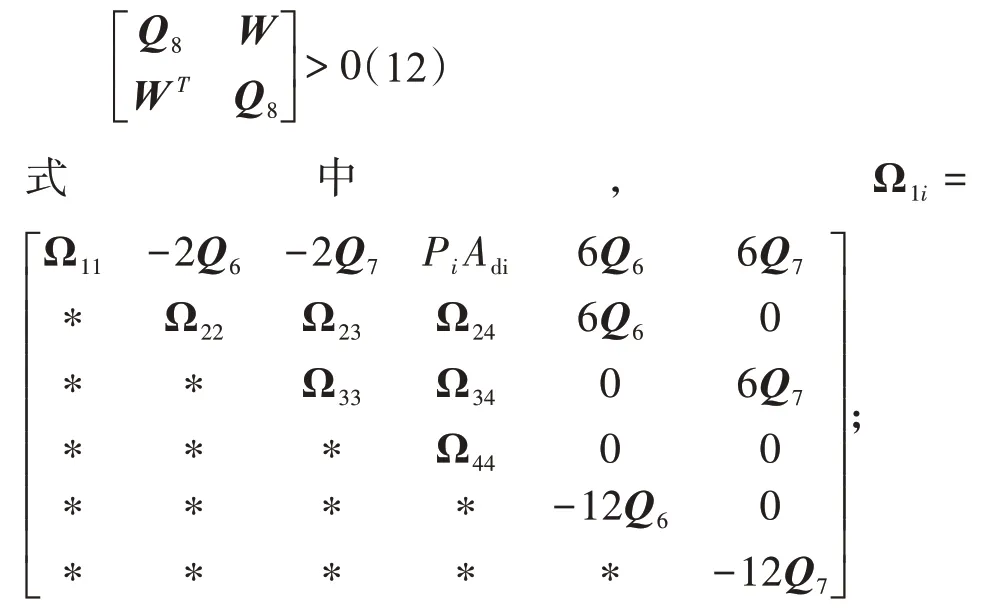
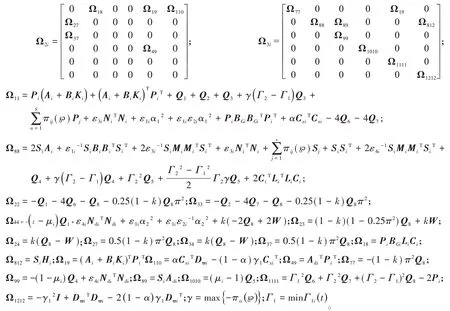
证明:首先,设计一个新的李雅普诺夫函数:
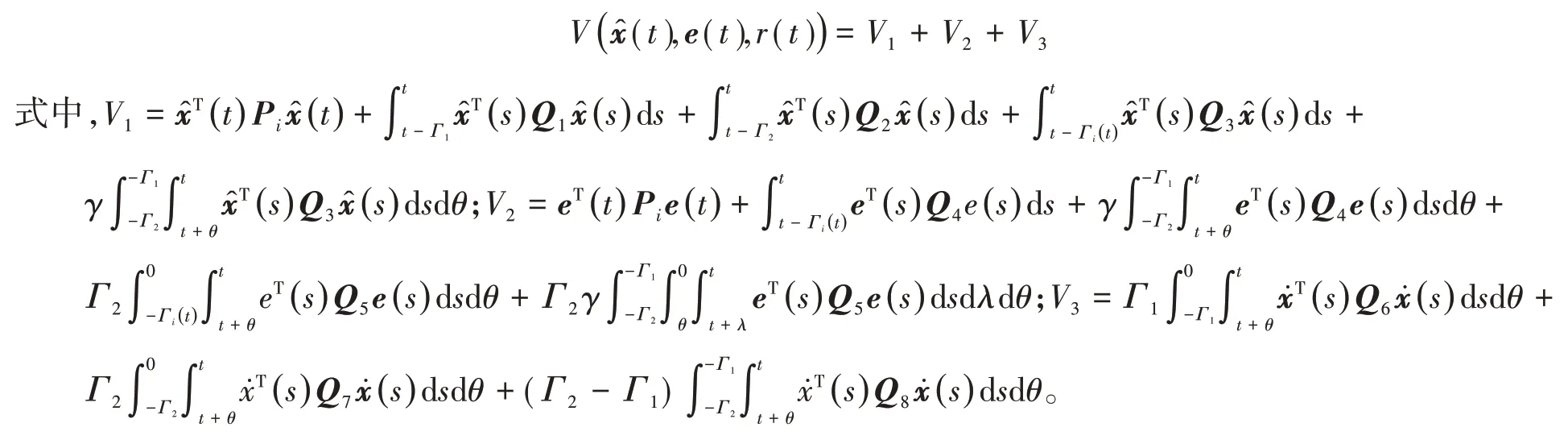
从李雅普诺夫函数中可得ℓV1:
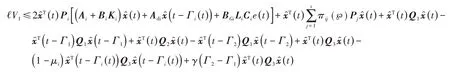
则ℓV2和ℓV3分别为
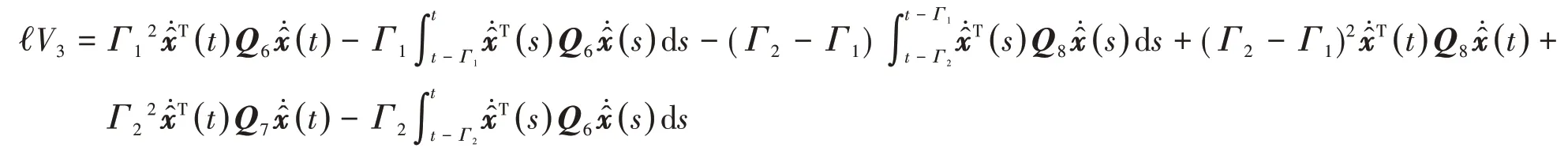
式中,πij≥0。
当i≠j,πii≤0时:
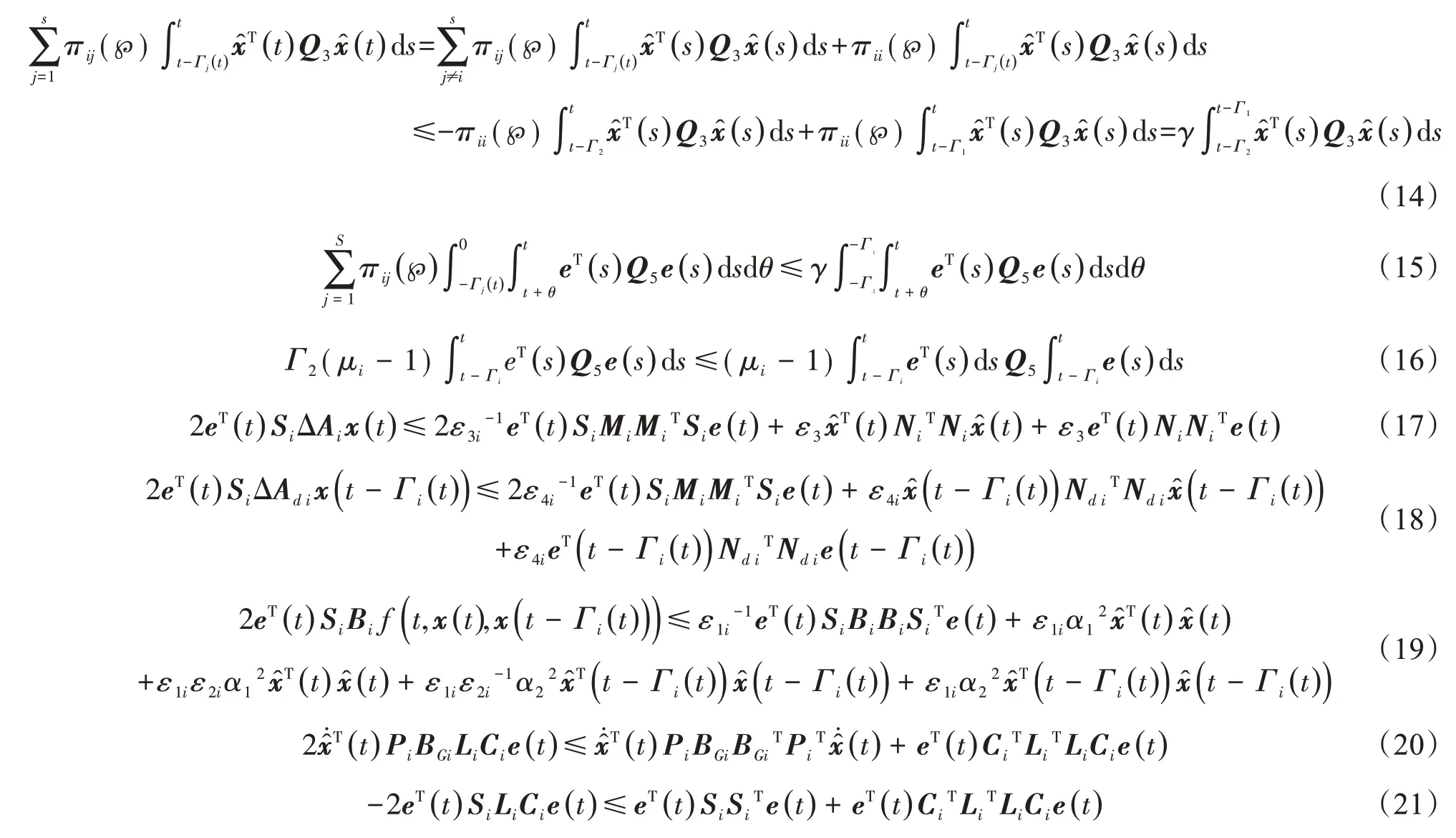
将式(9)引入ℓV3可得:

基于牛顿莱布尼兹公式可知:
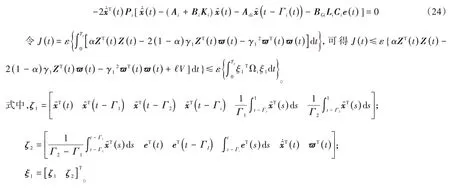
基于上述分析,当t>0 时,可得J(t)≤0,系统具有混合H∞和无源的性能,证毕。值得注意的是当ϖ(t)=0时,闭环系统也是稳定的。

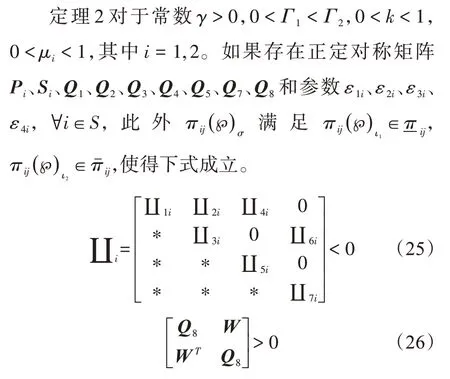


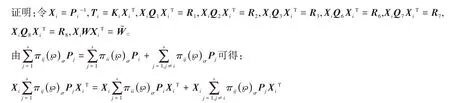
基于schur 引理,式(11)左右分别乘对角阵diag{Xi Xi Xi Xi Xi Xi Xi I I I Xi I}和其转置。可知式(11)等价于式(25)。
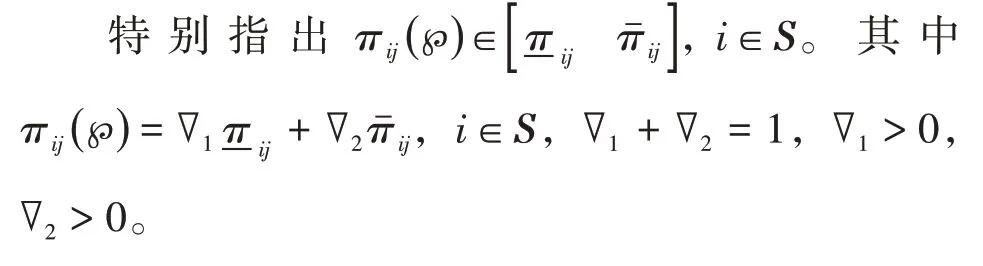
2.3 滑模控制率的设计
定理3滑模控制率为
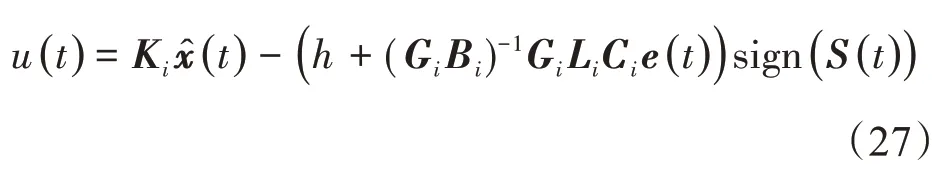
式中,h为特别小的常数且满足h>0,则可以到达滑模面S(t)=0上。
证明:选择李雅普诺夫函数
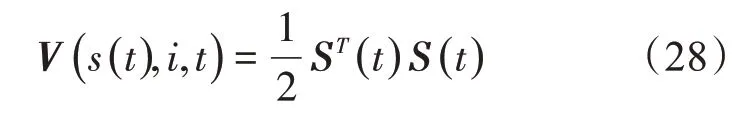
对式(28)进行求导可得:
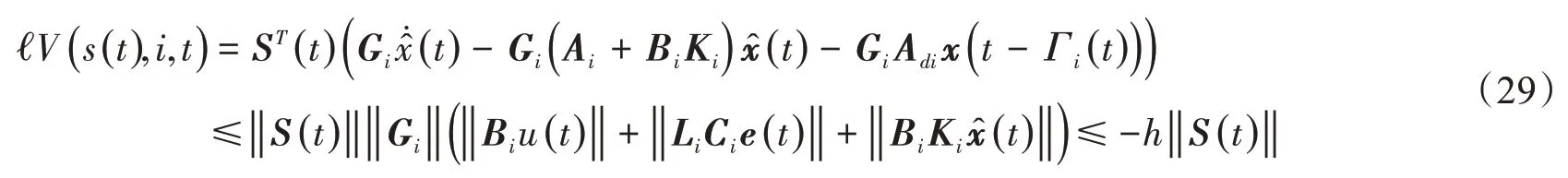
由式(29)可推出

3 数值仿真
通过仿真证明理论的可行性和合理性。


其他参数为ε1i=ε2i=0.5、ε3i=0.4、ε4i=0.2、a=0.5、d1=0.1sint、d2=0.6 cost;时滞导数的最大上界为μ1=0.2、μ2=0.25,且参数γ1=1;外部扰动ϖ(t)=0.2⋅exp(-100t);非线性函数fi(t,x(t),x(t-Γi(t,rt)))=0.05sin(100x1(t))。
基于线性不等式,可得K1=[11.215 6-3.966 8]、K2=[8.572 2-3.324 2]、。
图1 至图5 分别为例1 的闭环系统状态图、切换函数、系统的控制输入、观测系统状态并包含系统的切换信号和系统的误差轨迹。
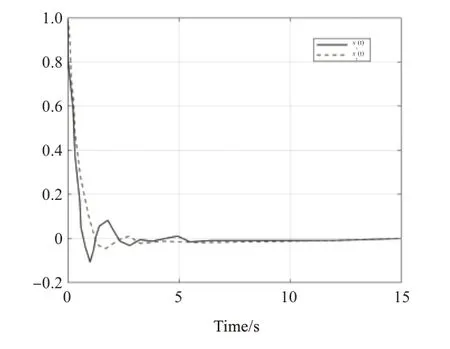
图1 例1的状态轨迹
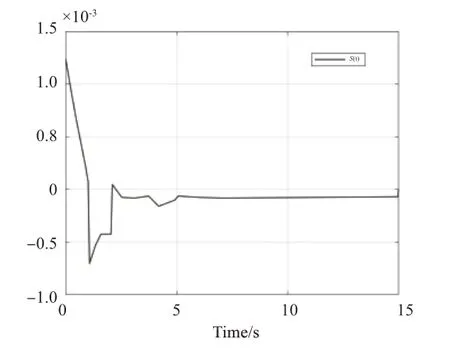
图2 例1的切换函数

图3 例1的控制输入
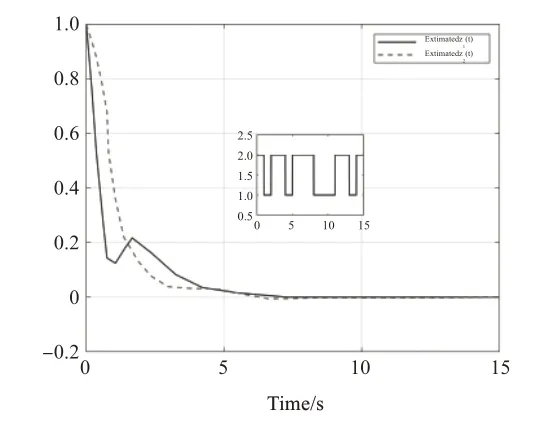
图4 例1的观测状态
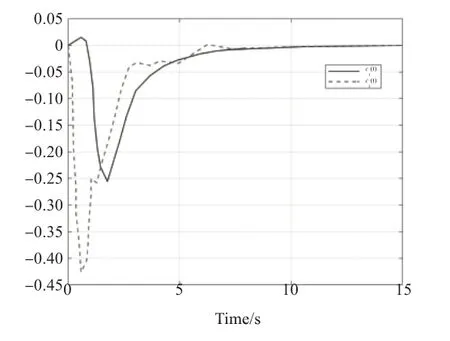
图5 例1的估计误差

表1 参数在不同模态下的取值
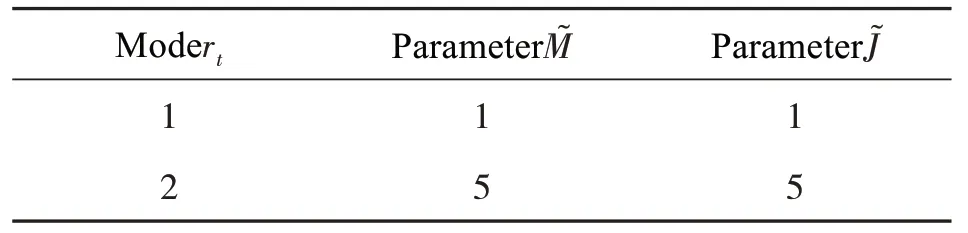
表1 参数在不同模态下的取值

表2 单连杆机器人手臂模型中参数的意义和大小

表2(续)
图6 至图10 分别为例2 的闭环系统状态图、切换函数、系统的控制输入、观测系统状态并包含系统的切换信号和系统的误差轨迹。
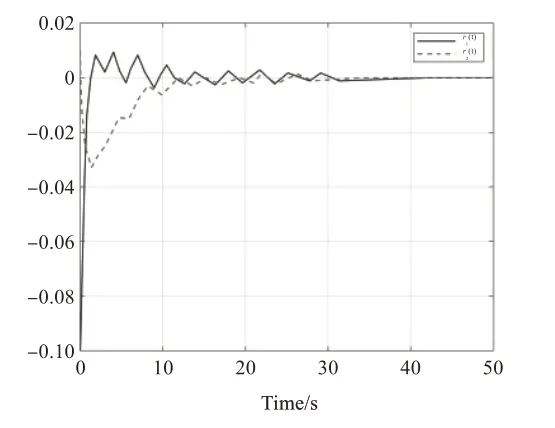
图6 例2的状态轨迹
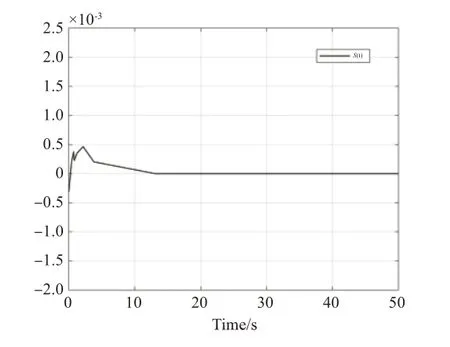
图7 例2的切换函数
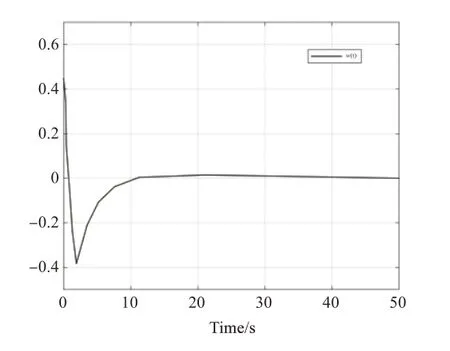
图8 例2的控制输入
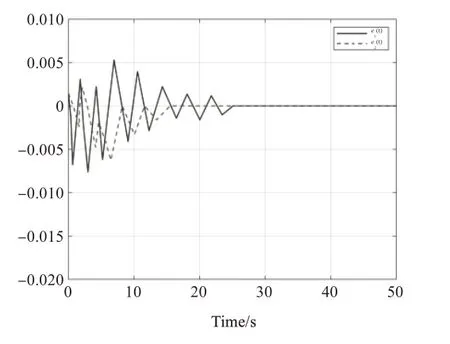
图9 例2的观测状态
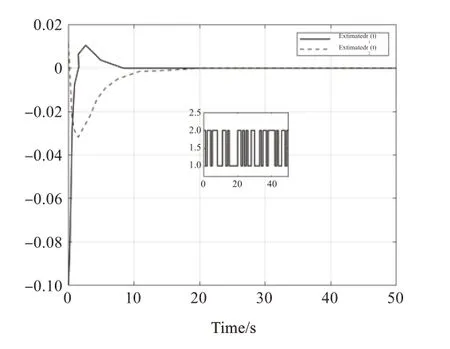
图10 例2的估计误差
4 结论
针对一类具有时变时滞、扰动和不确定因素的非线性半Markov 跳变系统,本文研究了观测器设计和滑模控制问题。所得结论如下:
1)设计了一类模态依赖的Lyapunov 函数,得到了充分条件,使半Markov 跳变系统实现渐进稳定,在存在外部干扰并具有混合H∞和无源的性能的情况下得到的充分条件有更低的保守性;
2)基于线性矩阵不等式,得到了控制器的增益矩阵,最终通过仿真证明了该方法的优越性和合理性。
