动态混合局面评估MCTS 算法在爱恩斯坦棋中的应用
2022-08-19宋英健侯荣旭孙嘉荣史广阔
宋英健,侯荣旭,孙嘉荣,史广阔
(沈阳工程学院 信息学院,辽宁 沈阳 110136)
计算机博弈是研究人工智能领域的一个重要分支,同时也是各个科研领域方面重点研究的对象,其目的是构建一个具有AI智能的算法,使之可以像人类选手一样进行对战、博弈[1]。计算机博弈程序一般由评估函数与优化搜索算法两部分组成,同时配有棋局评估、法生成、开局库与残局库开发、博弈树搜索、系统测试及参数优化等核心技术要点[2]。
1 爱恩斯坦棋介绍
爱恩斯坦棋是2004 年由德国人英戈·阿尔托夫发明的一种双人非完备信息类博弈游戏。棋盘为5×5 的方格形棋盘,每一个方格代表一个棋位,棋盘的左上角为红方棋子位置,棋盘的右下角为蓝方棋子位置;双方共持有6 枚棋子,棋子序号为1~6,顺序在双方出发区棋位可以无序任意放置;对局开始由红方先抛出骰子,移动棋子的标号与骰子点数相对应,如果棋盘中不存在与骰子点数相对应的棋子,则可以顺着点数向上或者向下查找,选择与之最相近的点数,移动该枚棋子;双方移动规则为红方只能移动目标棋子朝右方、下方、斜下方移动,蓝方只能移动目标棋子朝左方、上方、斜上方移动;在棋子移动的目标棋位上如有棋子(不论敌我),则移动本方棋子来覆盖该枚棋子,被覆盖的棋子从棋盘中移除。胜利的条件有两种,分别为移动到对方对角点和全歼对方棋子,爱恩斯坦棋无平局出现。
2 算法设计
对于构建一个计算机博弈算法,估值函数与搜索算法是不可或缺的。对于爱恩斯坦棋博弈系统来说,一方获胜的条件为吃掉对方全部棋子或到达对方对角线,通过完全模拟算法可以精准地预测棋子的目标棋位,从而获得胜利。模拟算法虽好,但是局限性也很大,主要受制于计算机的硬件性能。现有的计算机无法在短时间内计算出目标结果。所以,一般要对所使用的搜索算法加以改进。传统的搜索算法有很多种,如完全模拟算法、MCTS 算法、MAX-MIN 算法等。不同于传统的围棋、象棋等完备信息类游戏,爱恩斯坦棋中移动棋子需要投掷骰子,根据骰子的点数来确定移动的棋子。所以,对于带有随机性质的问题,Monte-Carlo 算法的适用度较其他传统算法更加契合,通过Monte-Carlo 算法,不需要模拟出所有的对局局面,仅需要有限次模拟抽样就可以获得较为准确的结果。
评估函数的好坏可以决定程序的落子位置。传统的静态评估局限性较大,这种局限性往往体现在对弈后期,程序并不能有效地判断出当前局面的最佳落子位置,程序的判断力往往不如人脑的判断力,这显然是不合理的。在此基础上提出了一种动态混合局面评估函数。经过多次对弈实验可知,使用改进评估函数的程序在后期的失误率要远远低于使用普通静态评估函数下的失误率。
2.1 爱恩斯坦棋常用算法
在传统的机器博弈中常被提到的算法有α-β剪枝算法、Monte-Carlo 算法、极大值极小值算法等。在全国大学生计算机博弈大赛中,大多数参赛选手的参赛程序均采用了α-β 剪枝算法或Monte-Carlo算法。棋力的高低与双方对算法的优化和硬件设备的性能有较大关系。
经过多种实验,Monte-Carlo 算法的搜索次数可自定并且搜索时间也可以进行设置。该算法在爱恩斯坦棋中通过有限次模拟对局后,计算出棋子移动的胜率,最终决定落子选择和落子方向。但此做法有一较大缺点,在模拟过程中双方完全随机移动,在有限次完全随机模拟中可能会得到与预期相差较大的移动结果,而且由于程序将对方假想为完全随机算法,程序计算得到的胜率偏高,这会影响程序的判断力并做出错误的决定。将Monte-Carlo算法优化改进与混合局面评估函数综合应用后,将会得到更加精确的结果,从而有效提高棋力。
2.2 Monte-Carlo算法
Monte-Carlo 算法又被称为模拟统计算法,其中最简单、最基本、最重要的一个概率分布是(0,1)上的矩形分布[3]。在C++中,采取随机模拟的方式来实现Monte-Carlo 算法。通过设置模拟次数,在搜索过程中不断地对双方进行完全随机模拟对弈,通过模拟对弈的胜场来计算模拟的胜率,模拟的次数越多,得到的胜率就越精确,最后经过胜率对比来筛选胜率最高的决策,从而达到有利于己方的局面。
在爱恩斯坦棋中,棋子的移动取决于骰子数。Monte-Carlo 算法可以用于优化模拟算法,用有限次模拟来进行抽样,从而获得较为准确的数据。以红方为例,骰子点数为4,程序首先判断4对应的棋子是否存活,如果存活则选中,反之则向上或向下遍历寻找与之最相近的棋子;若设置模拟次数为5 000,程序先取得当前棋子的所有着法,然后对所有着法的胜率进行判断比较。如正右方胜利次数为2 000,正下方胜利次数为100,右下方胜利次数为4 999,则正右方胜率为40%,正下方胜率为2%,右下方胜率为99%,通过比较胜率可以得到当前局面棋子4向右下方移动为最优走法。
本文中采用C++为编程语言,设置参数MC_CONSTANT 为模拟的总次数,设Eva 为模拟对弈中红方胜利的总次数,则胜率p(Eva)=Eva/MC_CONSTANT。设k为在MCTS 中模拟出正确决策的次数,ε为任意大小的正数,则

式(1)证明了当n趋于无穷大的时候,概率k/n收敛于s'/s。
2.3 动态混合局面评估函数
在程序运行过程中,需要有一个评估函数来对当前局面进行判断,从而得出最优落子点。传统的静态评估函数具有片面的特点。本文设计了一种动态混合局面评估函数,提出了进攻值、威胁值及距离价值的概念,通过多方面的混合评估来最终确定棋子的价值。
2.3.1 棋子移动概率计算
爱恩斯坦棋红蓝双方各有6枚棋子,每枚棋子在初始被抽到的概率均为1/6,随着对弈的进行,棋子陆续被覆盖吃掉,此时与骰子点数相近的棋子概率将会上升。发生吃子后,其他棋子的灵活性将会得到提高。所以,在对弈中常常采取舍弃其他棋子的办法来提高棋子的灵活性。每枚棋子被选中的几率为
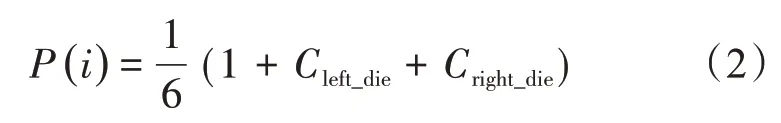
式中,P(i)为第i枚棋子被选中的几率;i为红方棋子的标号;Cleft_die为棋子序号左侧被吃子的数量;Cright_die为子序号右侧被吃子的数量。
2.3.2 棋子距离计算
棋子的价值与棋子所处位置有关,价值随着到对方对角的距离长短而改变,红蓝双方的距离计算公式为
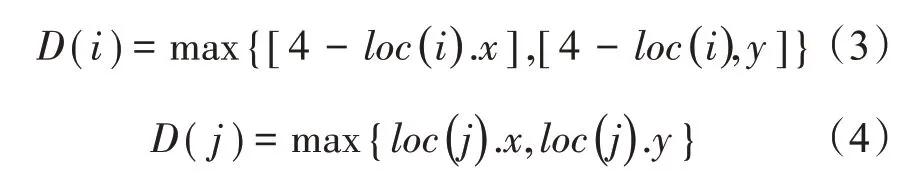
式中,D(i)为红方棋子距对方对角距离;D(j)为蓝方棋子距对方对角距离;loc()为红蓝双方棋子当前的坐标。
2.3.3 棋子动态价值计算
根据对弈经验和其他参考文献,棋子在边界与其他位置的动态价值不同,在边界的棋子距离对方对角的距离初始均为4,价值较小,但当边界的棋子距离缩短为2 时,棋子价值得到很大提升。棋子动态价值计算式为

2.3.4 进攻值计算
所谓进攻值是指当前局面下我方棋子产生的总价值的期望,红方进攻值为正数,蓝方进攻值为负数,当进攻值的绝对值越大时,说明当前局面对己方越有利。进攻值的计算式为
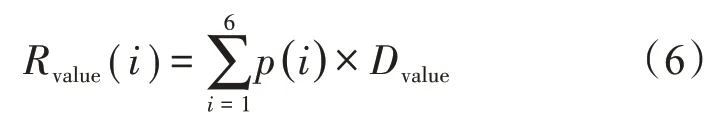
2.3.5 威胁值计算
威胁值是指对方的棋子将会对本方的局面产生的不利估值,威胁值越大说明对己方越不利。威胁值的计算式为
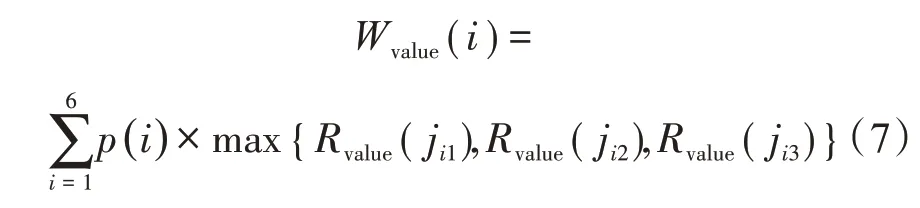
2.3.6 动态混合评估总体估值计算
不同于传统的评估函数,动态混合评估函数考虑了进攻值、威胁值及动态价值3 个方面因素,有效提高了程序的精准性和智能性,总体评估为当前局面所有棋子的综合总价值。如果综合总价值越大,说明局势对红方越有利;综合总价值越小,说明对蓝方越有利;当综合总价值为0 时,双方局势相同。综合总价值的计算式为
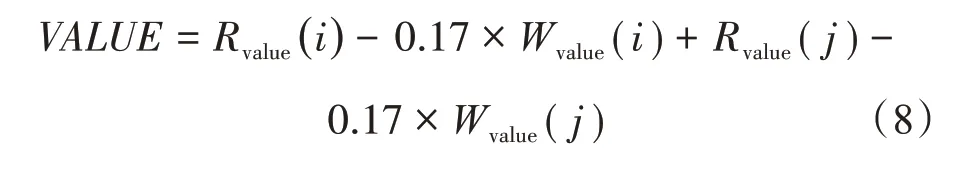
3 动态混合局面评估MCTS算法
动态混合局面评估函数主要用来加强Monte-Carlo 算法。融合了动态混合局面评估函数的Monte-Carlo算法在模拟对弈的过程中能够更加稳定,减少随机性,这在对弈的后期体现尤其明显。在模拟对弈时不再单纯地使用完全随机模拟,要接入动态混合局面评估函数,筛选掉胜率明显偏低的结点,提高了程序在单位时间内搜索的效率。在程序进行选子落子决策时,传统的评估函数仅看中进攻值,导致缺少防守能力;采取混合局面评估后,结合了进攻值、威胁值等多方面的因素,可以达到攻守兼备的效果。动态混合局面评估函数MCTS 算法流程如图1所示。
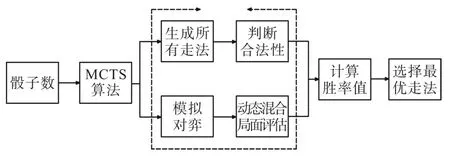
图1 动态混合局面评估函数MCTS算法流程
4 分析比较
4.1 系统实现
基于以上算法的研究,本文使用C++语言在vi‐sual studio 2019与Qt5.12.3环境下实现了一款基于动态混合局面评估MCTS算法的爱恩斯坦棋博弈系统。程序棋盘界面用QPainter 绘制,在Gps 类中,x1、x2、y1、y2 代表矩形区域。当value 值为0 时,代表该区域没有棋子;当value值为正数时,代表是红方的棋子;当value值为负数时,代表是蓝方的棋子。
棋子移动采用了mousePressEvent 事件。当鼠标进入5×5棋盘区域内并单击任意一枚棋子时,获取该区域内棋子的信息;如果鼠标在5×5棋盘区域外单击,则判断当前单击无效。当鼠标移动事件触发后,鼠标在向左或向右移动时,被单击棋子对应区域的x1、x2、y1、y2 也会随之增加或缩减。mouseReleaseEvent(鼠标释放事件)为当鼠标在某一个区域释放时,首先判断该棋子是否合法,如果该走法合法则成功移动棋子。
图2 为本系统用QT 制作的主界面,主要分为棋盘和搜索算法两部分。棋盘控制部分包括棋盘表示、界面交互、对局悔棋、对局计时、AI 胜算估值、历史记录及棋盘保存7 大部分。程序可以切换AI 算法并实现自对弈,在进行对局之后,可以自动生成棋谱和着法信息,方便统计比较。算法部分包括MCTS算法和动态混合局面评估MCTS算法。
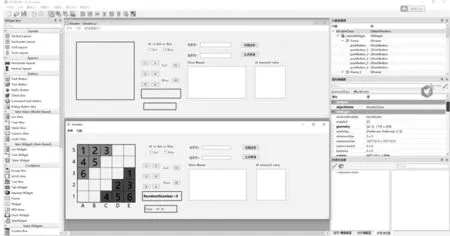
图2 爱恩斯坦棋博弈系统QT界面
4.2 实验分析
本文实验以表格数据和直方图的形式展示Monte-Carlo算法与动态混合局面评估MCTS算法在爱恩斯坦棋中的应用效果。本次对弈实验以模拟次数MC_CONSTANT 和算法种类Type 为自变量,两种算法的模拟次数设置为5 000次和10 000次。
4.3 结果分析
在实验之后,记录对弈的平均时长及胜率情况,制成的数据如图3所示。实验结果有效地验证了动态混合局面评估MCTS算法相比于传统的MCTS算法,在胜率和时间上均有较大的优势。若每局模拟次数固定为5 000,则动态混合局面评估MCTS 算法耗时为MCTS算法的73.5%,而胜率为64.5%。
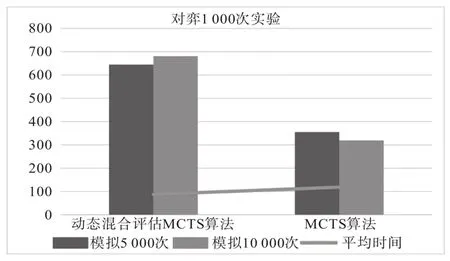
图3 对弈实验数据
由此可得,在爱恩斯坦棋中,动态混合局面评估MCTS算法可以有效提高搜索效率和对弈胜率。
5 结论
本文采用动态混合评估函数代替传统评估函数,并将动态混合评估函数与Monte-Carlo 算法相结合,有效地提高了程序的智能性和效率。经过改良后的算法考虑了对弈当前局面的多种因素,不采取单一的棋盘估值,而是采取动态估值和总体估值来判断当前的局势,从而使程序做出正确的决策,减少失误和随机性。
经过结合后的算法胜率和搜索效率显著高于传统算法。在后续的工作学习中,也可以结合机器学习、深度学习等其他智能算法来进一步提高程序的AI等级,这也是值得深入研究的[4]。
