电力机械关键零件加工状态检测与分析
2022-08-19康群英刘劲涛
康群英,刘劲涛,王 琳
(沈阳工程学院a.能源与动力学院;b.机械学院,辽宁 沈阳 110136)
电力机械在工业领域中被广泛应用,而其关键零件在加工过程中会出现磨损等问题,从而降低工作效率,造成一定的经济损失。对此,人们采用直接检测的方法,即直接测量关键零件的实际磨损程度,通过光学和图像处理技术测量电力机械设备的破损情况。但是这种检测方法只有在电力机械设备不工作时才能进行,属于离线检测,达不到实时检测的效果。
国外对此类问题的检测方法研究比较早。KULJANIC E 等人成功地运用了基于小波包自回归谱(WP-AR)的分析方法来对关键零件的磨损状态进行检测,通过对加工过程中的信号进行分析,获得了有效的关键零件磨损特征量,进而准确地判别出零件的磨损状况;MANNAN M A 等人基于树型的小波变换方法实现对关键零件磨损图像的分离,将分离后的各个子图的能量定义为神经网络特征矢量,通过初始值训练和纹理分割,对关键零件的加工状况进行预报,并验证了该方法的优越性。
国内对此类问题的研究比较晚。庄子杰、汤为等人对信号采用统计分析和功率谱分析的方法,获得了反应关键零件磨损变化的特征值,并验证了该方法的准确性;谢秀娴利用神经网络的非线性映射原理,推导出了关键零件的磨损状态和声发射信号的特征向量之间的对应关系,并利用BP 神经网络对关键零件的磨损状态进行了识别;舒服华利用小波变换对加工过程中与关键零件磨损有关的信号进行了分析,并研究了关键零件在加工过程中的磨损状况,该方法为关键零件磨损状态的在线检测和实时补偿提供了准确的依据。
发电厂对电力机械关键零件的加工精度要求较高,为了保证生产出的零件符合精度要求,需要对加工刀具进行在线检测,判断刀具是否发生磨损或故障等问题。而在检测过程中,因受到加工环境的影响,采集到的振动信号含有噪声,难以提取刀具的故障特征。针对这一问题,可以采用小波变换对振动信号进行消噪,并通过Smoothing Spline 拟合的方法,对离散试验数据进行函数拟合,使振动信号曲线达到平滑的效果,更好地观测出刀具加工时间和振动信号幅值之间的非线性关系,找出其运动规律。通过曲线拟合后的振动信号幅值数据,建立刀具健康诊断模型,可以实时检测刀具的磨损状态,起到预判的效果。电力机械设备检测系统原理如图1所示。
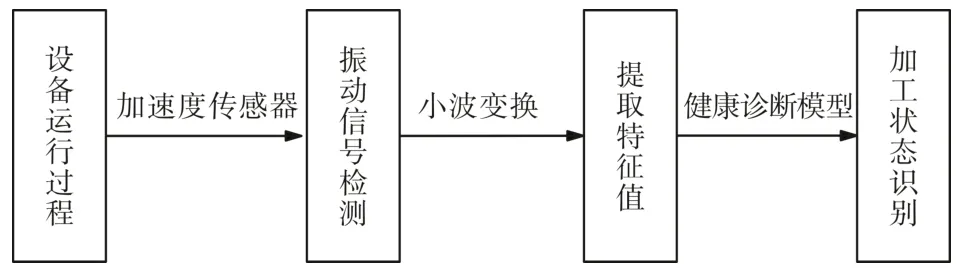
图1 电力机械设备检测系统原理
1 试验信号采集与分析
1.1 试验装置
振动信号采集与分析试验台由数控加工装置和振动检测装置组成。加工装置为智能多轴立式加工中心,刀具为2FR3.0×D6×75L(刃数刃径×柄径×全长)55°铝用球头刀,工件的材质为6061 铝材质,直径为90 mm,高度为80 mm。新刀具和磨损刀具的状况如图2所示。

图2 铝用球头铣刀
振动检测试验装置采用振动信号数据采集仪,型号为INV3018CT,通过机床主轴上安装的3个加速度传感器分别检测刀具在X 方向、Y 方向和其他方向的振动信号。然后,在PC 端用DASP 软件对数据进行采集与分析。加速度传感器的具体安装位置如图3所示。

图3 加速度传感器的安装位置
1.2 振动信号的采集与分析
由于加工环境的影响,采集到的振动信号中含有噪声,所以要对试验数据进行预处理,剔除原始数据中无意义的有害噪声,提高信噪比。在相同的切削要素下,根据所采集的新刀具和磨损刀具的振动信号幅值的大小,可以判断出其磨损情况。
试验设置的采样频率FS 为1 024 Hz,分析频率AF 为400 Hz,机床主轴转速n为4 000 r/min,进给速度f为200 mm/min,切削深度h为0.3 mm。
1.2.1 振动信号的时域分析
时域分析是控制系统在一定的输入下,根据输出量的时域表达式分析系统的稳定性、瞬态和稳态性能。因此,通过该分析方法能够对多通道的信号的时域波形进行分析,可以显示出信号在时间域上的幅值波形,从波形图上能得到信号在各时间段上的幅值大小。刀具振动信号幅度随时间变化情况如图4所示。
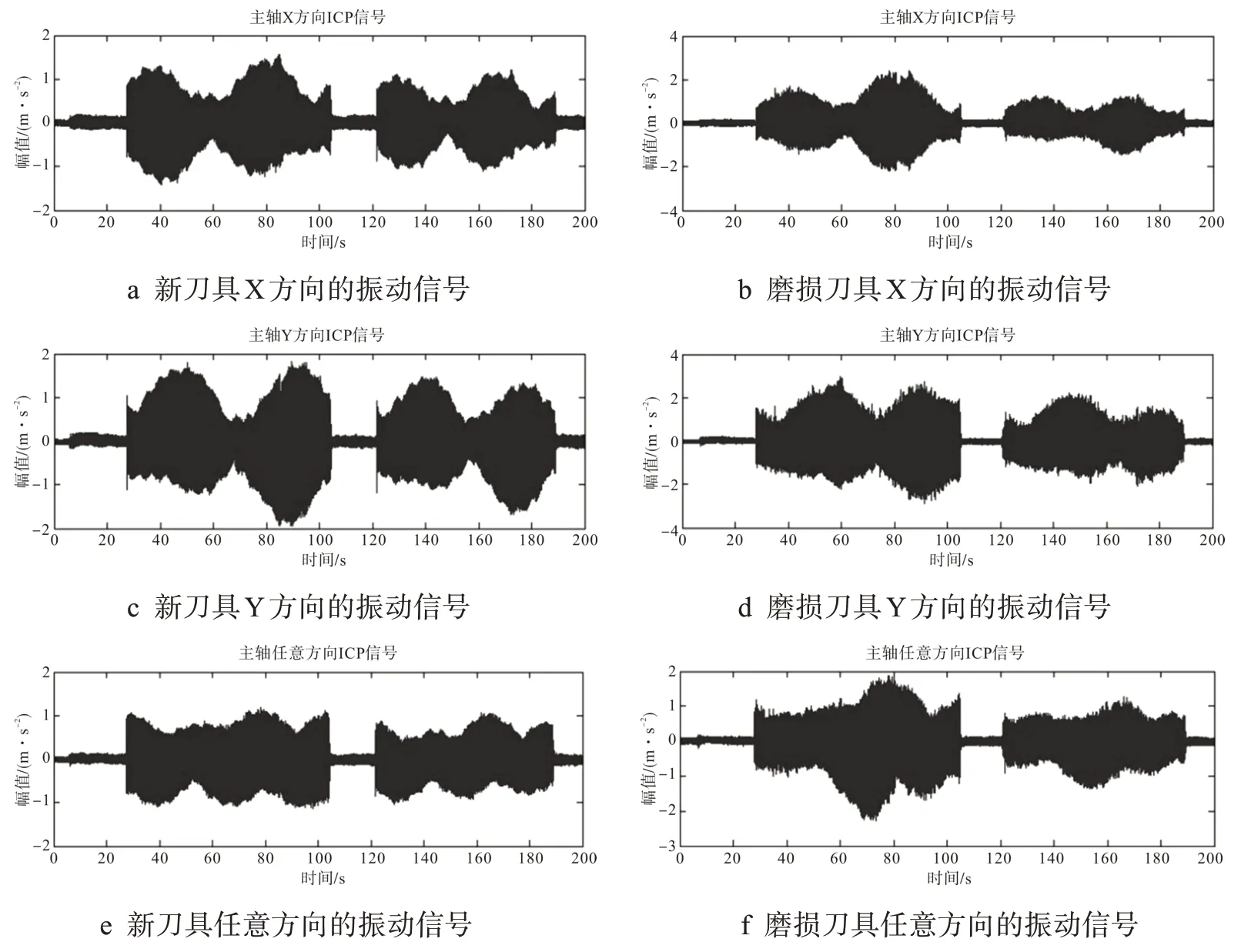
图4 时域分析
由时域分析可知,刀具进行了两个加工阶段,磨损刀具在3 个方向上的振动信号幅值明显高于新刀具的振动信号幅值,而Y方向的振动特性要更为显著,说明刀具在Y 方向上的加工状态更为剧烈。所以,要重点检测刀具在Y 方向上的振动信号。此外,磨损刀具在Y方向上的振动信号幅度的绝对值超过了2 m/s2,说明刀具已经处于严重磨损状态。
1.2.2 振动信号的频域分析
频域分析是在频域范围内应用图解分析法评价系统性能的一种工程方法。因此,为了研究刀具振动信号的内在规律,需要分析振动信号的周期性,此时要将信号从时域变换到频域,所得频谱中的每个频率都对应振动信号的1 个周期谐波分量。对刀具进行功率谱分析,可以反映各谐波分量的能量,其分析结果如图5所示。
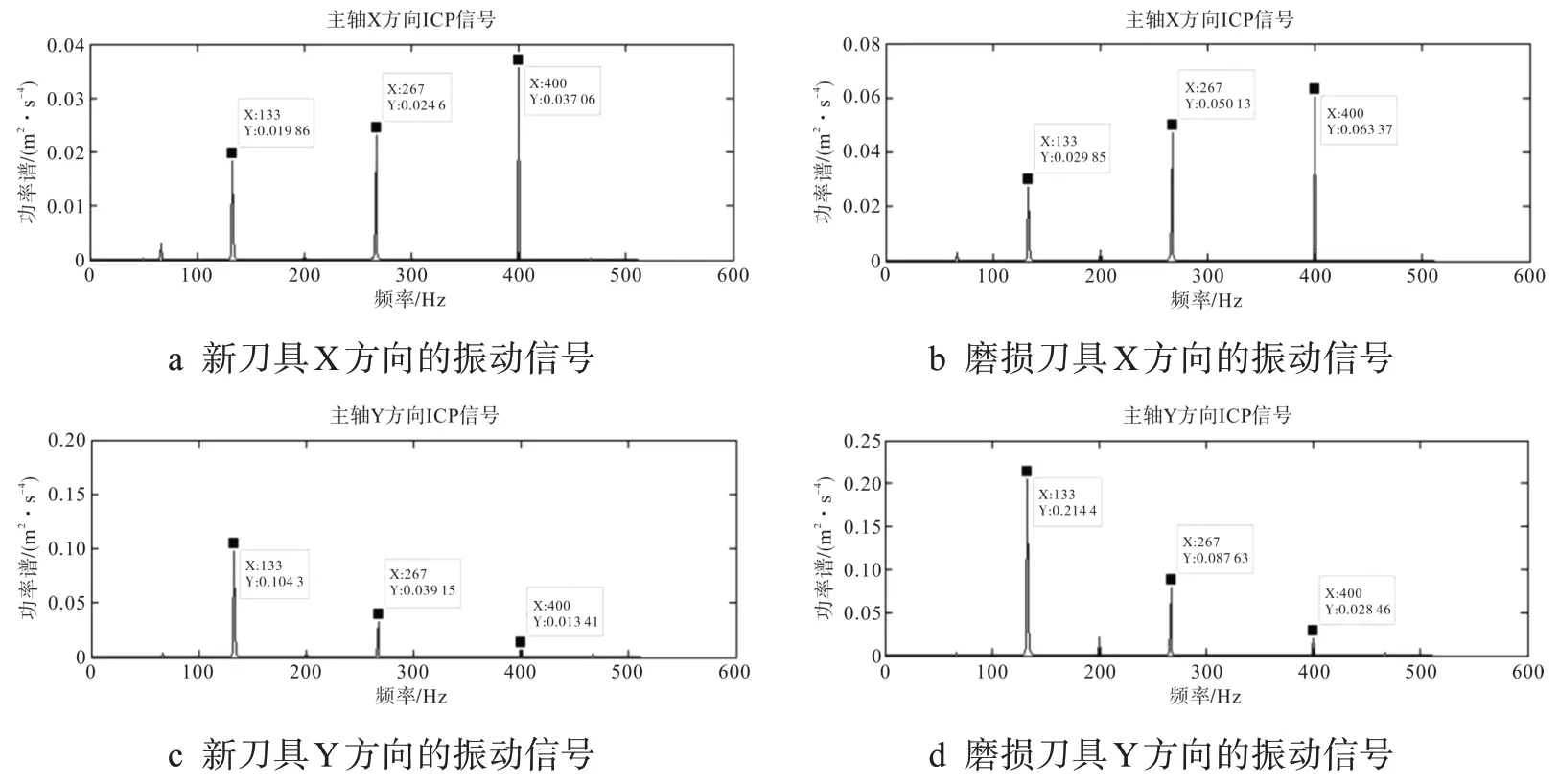

图5 功率谱分析
由功率谱分析可知,当振动信号频率分别为133 Hz、267 Hz 和400 Hz 时,刀具发生了3 次共振现象;磨损刀具在3 个方向上的峰值能量要高于新刀具,而在Y 方向的峰值能量最为显著,说明刀具在Y 方向上的加工状态最为剧烈。此外,刀具在Y方向上的初期磨损阶段的峰值能量由0.104 3 Hz跳跃到了急剧磨损阶段的0.214 4 Hz,此时刀具已经处于严重磨损状态。
1.3 信号的小波变换
1.3.1 小波分解
小波变换可以把刀具的振动信号图像分解为低频信息和高频信息。由上述分析可知,刀具在Y方向上的振动特性最为显著,应对刀具在Y方向上的振动信号图像进行多尺度分解。Daubechies(dbN)小波分解是一种离散正交小波,通过db4 小波基对刀具振动信号进行3 层尺度小波分解,并显示新刀具和磨损刀具分解后的低频和高频信息。小波分解结果如图6和图7所示。
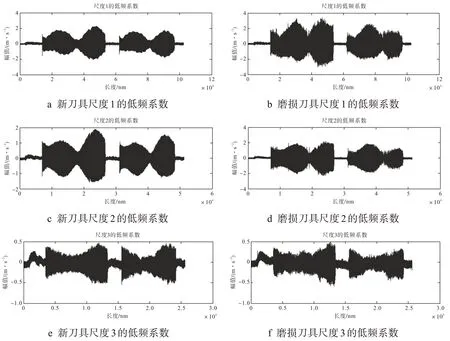
图6 小波低频系数分解
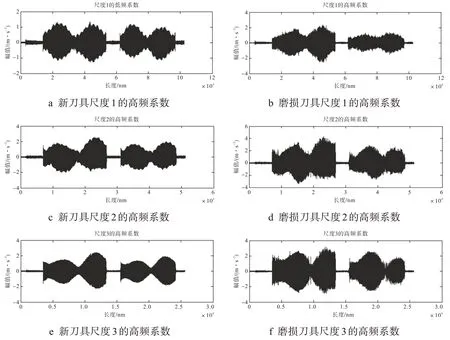
图7 小波高频系数分解
通过小波分解可以看出振动信号图像db4 小波3 层分解之后的高频信息和低频信息,从多尺度逐步观察振动信号,并对振动信号进行滤波处理,从而表征振动信号的局部特征,还有利于检测振动信号的瞬态或奇异点。
1.3.2 小波重构
在使用wavedec函数对小波进行了db4分解以后,使用waverec 将原信号重构,达到去除有害噪声的目的。刀具振动信号图像经小波重构的分析结果如图8所示。
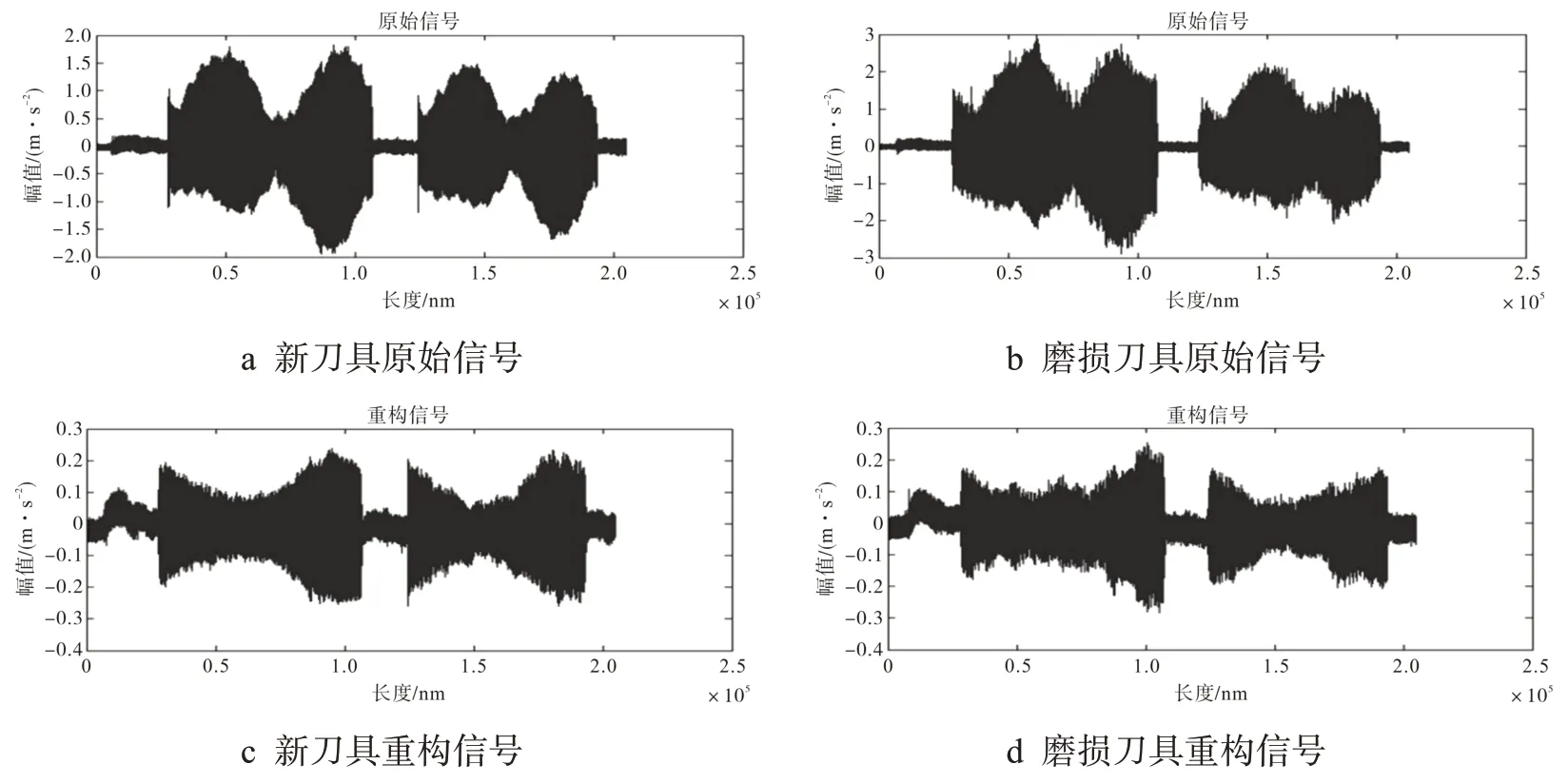
图8 小波重构
小波重构信号对高频信号进行了过滤,剔除了原始信号中无意义的有害噪声,提高了信噪比,从而更加清楚地观测出刀具振动信号的变化情况。
1.3.3 振动信号的时-频分析
时-频分析的主要研究对象是非平稳信号或时变信号,用于描述信号的频谱含量随时间变化的情况。该方法能够同时观察刀具振动信号在时间域和频率域的联合分布信息,清楚地表达出刀具振动信号的频率随时间变化的关系,同时考虑两个方面的性能,从而更好地观察出刀具振动信号的局部特性。刀具在Y 方向上的振动信号时-频分析结果如图9所示。

图9 时-频分析
由时-频分析可知,振动信号主要是由频率为140 Hz 和270 Hz 附近的周期信号组成,新刀具和磨损刀具在时间域和频率域上的振动信号的特征明显呈现,有效地克服了傅里叶分析时域和频域完全分离的缺陷。由此可见,该方法可以同时描述刀具的振动信号在不同时间和频率的能量密度或强度,给出了刀具的振动信号在各时刻的瞬时频率及幅值,并对其时-频滤波和时变信号进行研究。
2 刀具健康诊断模型
2.1 模型准备
在对振动信号进行时域分析后,发现时间域和振动信号幅值之间属于非线性关系,难以找出刀具振动信号的特性。因此,采用曲线拟合的方法对原始信号的时域图像进行拟合处理,以便观察出刀具振动信号幅值的变化情况,并提取有效的特征值;同时,选取振动信号的特征向量,建立健康诊断模型,利用该模型实时检测刀具的加工状态,起到预判的效果。
2.2 模型建立
通过Smoothing Spline对振动信号中的离散试验数据进行函数拟合,即在原本的拟合误差基础上加上λ∫{fn(t)}2dt,从而使曲线达到光滑的效果。在Smoothing Spline 拟合中,参数p∈[0,1],p的取值越大,拟合结果就越倾向于经过所有的点,此时p=1。对新刀具和磨损刀具在Y 方向上的振动信号进行拟合,其平滑样条曲线拟合的结果如图10所示。

图10 平滑样条曲线
由拟合后的曲线可知,信号振幅更加平滑,能够明显地看出刀具振动信号的特性,从而使新刀具和磨损刀具的试验对比更加显著。从分析结果可知,在27 s~104 s 和122 s~188 s 时,刀具处于两个加工阶段;当拟合后的振动幅度绝对值在0~1.5 m/s2时,刀具处于初期磨损阶段;当拟合后的振动幅度绝对值在1.5 m/s2~2 m/s2时,刀具处于正常磨损阶段;当拟合后的振动幅度绝对值超过2 m/s2时,刀具处于急剧磨损阶段。
2.3 模型求解与分析
在Matlab 中使用Smoothing Spline 拟合工具,可以得到SSE(和方差、误差平方和)、R-square(确定系数)、Adjusted R-square 和RMSE(均方根)参数,以此判定拟合的效果是否最佳,如表1所示。

表1 光滑曲线拟合统计参数
由表1 可知,在SSE 中新刀具的数值更小些,说明光滑曲线拟合效果更好,数据预测也更成功;在R-square 中,磨损刀具的数值更趋近于1,其参数变量的释放能力越强,拟合效果越好;在Adjust‐ed R-square 中,磨损刀具的数值更趋近于1,说明其匹配的效果更好,当在模型中添加附加系数时,Adjusted R-square通常是适合质量的最佳指示器;在RMSE中,新刀具的数值更小,拟合的误差更小,效果更好。
为了更好地找出刀具振动信号的特性,判断出刀具加工磨损的程度,需要一些有效参数。应用电脑端的DASP 软件,可以对采集到的试验数据进行幅域指标统计,该功能可以计算出振动信号的平均值、方差、标准差、均方值和有效值。
以刀具在主轴Y 方向上的振动信号为主要研究对象,使用幅域指标统计功能后,得到5 组刀具振动信号幅域指标统计参数,如表2和表3所示。
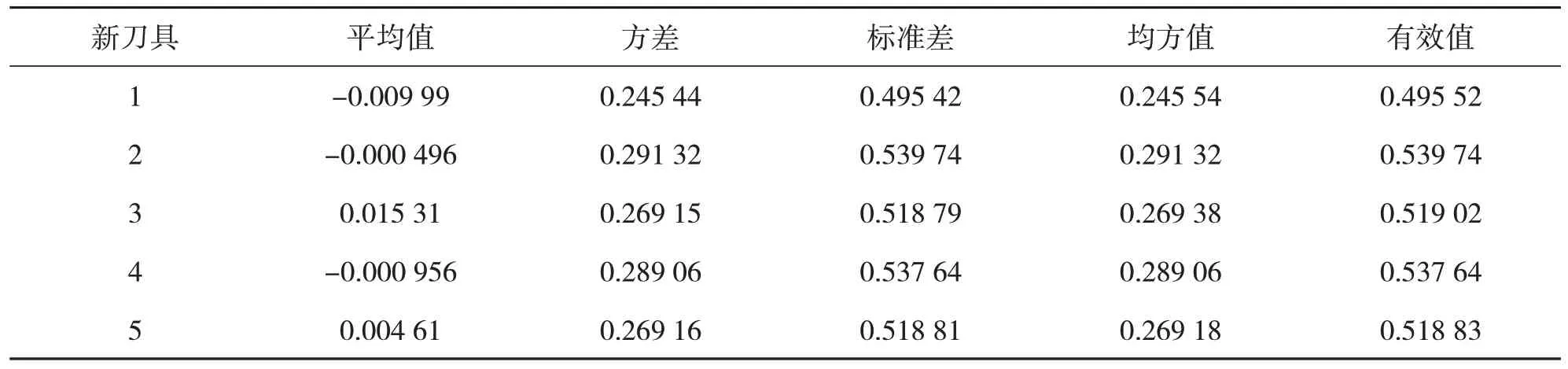
表2 新刀具幅域指标统计 m/s2
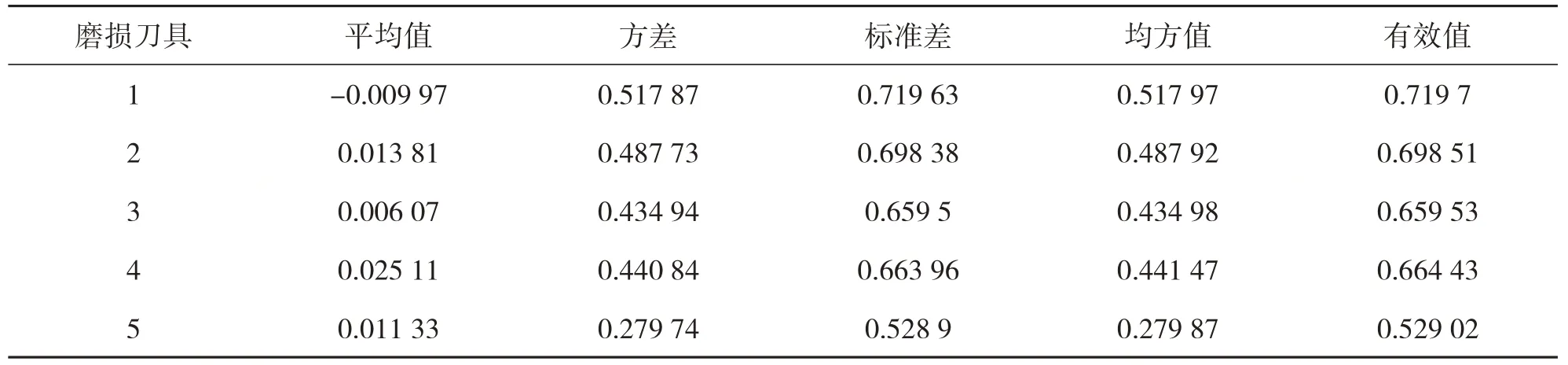
表3 磨损刀具幅域指标统计 m/s2
由表2 和表3 可知,磨损刀具在平均值、方差、标准差、均方值和有效值上的幅值要远大于新刀具,当检测到刀具振动信号的幅域指标数值超过磨损刀具的数值时,可以判定刀具处于严重磨损状态。
3 仿真振动信号
根据刀具在主轴Y方向上的振动信号特性,以及在急剧磨损阶段时刀具振动信号的时域特点、频域特点和联合时-频域特点,通过Matlab 软件中的Simulink 模块创建一个刀具振动信号发生系统,其 仿真模型如图11所示。

图11 刀具振动信号发生系统
刀具振动信号发生系统的原理是通过信号发生器和白噪声生成一个随机振动信号,依靠时钟模块来计算当前的仿真时间,刀具振动信号仿真时间设置为200 s:当仿真时间小于27 s 时,输出为合成的随机振动信号,模拟刀具处于空载加工阶段;在27 s~104 s 时,时间比较器发生变化,控制开关控制输出合成的随机振动信号乘以增益以后的信号,模拟刀具处于加工阶段;在104 s~122 s 时,时间比较器1 发生变化,控制开关1 输出最初的随机振动信号,模拟刀具处于空载加工阶段;在122 s~188 s 时,时间比较器2 发生变化,控制开关2 输出合成的随机振动信号乘以增益以后的信号,模拟刀具处于加工阶段;当仿真时间大于188 s 时,时间比较器3 发生变化,控制开关3 输出最初的随机振动信号,模拟刀具处于空载加工阶段。该仿真模型运行后,通过示波器观察到的仿真结果如图12所示。
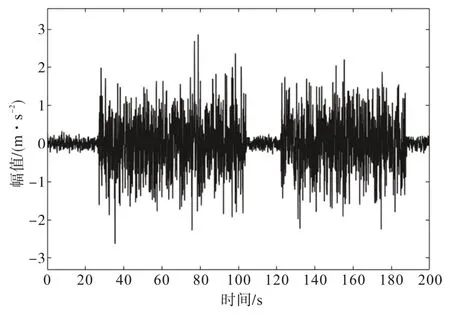
图12 仿真刀具振动信号
由图12 可知,刀具经历了2 个加工阶段和3 个空载运行阶段。该方法可以模拟出刀具的实际加工状态,具有更加灵活方便的操作过程,可以取代硬件仪器设备,降低成本。
4 结论
1)对采集到的振动信号进行时域分析、频域分析和联合时-频分析,并利用小波变换功能对原始信号进行分解与重构,剔除有害噪声,提高信噪比。
2)运用Matlab软件中的Smoothing Spline模块对刀具振动信号中的离散试验数据进行函数拟合,能够使振动信号曲线变得更为光滑,从而可以明显看出刀具加工时间和振动信号幅值之间的非线性关系,找出振动信号的运动规律,提取出有效的特征值,并选取刀具发生故障时的特征向量,建立刀具健康诊断模型。
3)应用Simulink 仿真模块创建刀具振动信号发生系统,通过信号发生器和白噪声生成一个随机振动信号,模拟刀具处于空载运行阶段;在该仿真模型中添加相应的增益模块,可以模拟刀具处于加工阶段;最后,通过示波器显示出在整个加工过程中刀具振动信号的变化情况。
