单兵晃动基座QUEST对准算法

张 祎，丁立波

（南京理工大学 机械工程学院，南京 210094）

单兵火箭弹通常采用跪姿或站姿发射，在对准过程中人体难免产生晃动，在这种干扰下惯性元件输出信息不止包含重力加速度以及地球的自转角速度，还包含了晃动产生的加速度与角速度干扰，使得捷联惯导难以在保证精度的条件下实现快速对准。

常见的惯性元件初始对准算法包括双矢量定姿法（three-axis attitude determination，TRAID）和多矢量定姿法（quaternion estimator，QUEST）。传统的TRAID算法［1］选取地球自转角速度和重力加速度作为定姿的双矢量，但由于晃动产生的角速度远大于地球自转角速度，以及实际惯性元件的精度一般无法测量到地球自转角速度，使得这种方法并不适用于晃动条件下的初始对准。秦永元等［2］考虑到传统双矢量定姿的问题，通过坐标系的分解，将测量地球自转角速度转化为计算重力矢量在惯性空间内的旋转，并在摇摆台上进行了验证，后续有关晃动条件初始对准问题的研究大多在此基础上进行。王勇军等［3］提出了最优TRAID（optimal-three-axis attitude determination）算法，该算法选取不同的矢量作为基准，进行两次姿态矩阵的求解，并根据两个矢量的方差特性对两个姿态阵做加权处理，但优化后对准精度与对准时间的提升并不明显。双矢量定姿通常只依靠两个时刻的重力信息进行对准，信息利用率不高，Silson［4］将比力在不同时间段积分得到多组速度矢量，构建多组观测矢量，将初始对准问题转化为最小二乘条件下的多矢量定姿问题，即Wahba问题。Shuster将Wahba问题写成四元数形式使得QUEST算法广泛应用于惯性测量单元这一类连续观测矢量的传感器。袁群哲等［5］对TRAID算法和QUEST算法进行精度分析，发现在观测矢量等精度的条件下QUEST算法精度明显优于TRAID算法。以上研究均是针对车载［7-8］或舰载［9］晃动情况下，而没有针对单兵人体晃动条件下的研究。

本文针对人体晃动下的快速初始对准问题，参考典型海况模型，对人体晃动条件进行建模，分析该条件下QUEST算法对准姿态角的收敛情况，以及蒙特卡罗仿真下的姿态角误差均值与均方差。并将姿态角误差加入到弹道仿真中，验证是否满足打击精度条件，旨在确定适合于单兵晃动基座快速初始对准的方案。

1 QUEST算法基本原理

1.1 Wahba问题

Wahba提出了解决姿态估计的方法，建立最小二乘的损失函数，将姿态估计问题描述如下：如果在惯性坐标系内有n个单位矢量，分别记为vi，i=1，…，n；在惯性元件中测得这些单位矢量的值为ui，那么姿态估计问题可以转换为如何找到一个旋转矩阵R，使得误差函数L最小，其中ωi为权重。

化简之后得到：

可以看出，若想要L取最小值，需要使tr（FRT）最大。

Shuster在1979年将四元数的理论融合到求解姿态估计问题中，并用四元数的形式改写tr（FRT）。

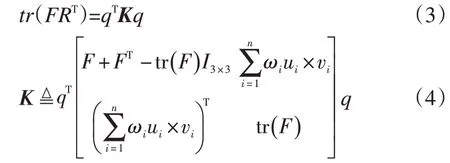
其中姿态变换四元数q的最优值就是矩阵K的最大特征值对应的特征向量。

1.2 基于四元数描述的QUEST问题

首先定义四元数的乘法。一般四元数的表达方式如下：

并记η=[η1η2η3]。对于任意两个四元数p、q，四元数乘法可表示为：

将u和v之间的转化关系写成四元数形式：

其中q表示u到v的变换四元数，根据四元数的性质整理得到：

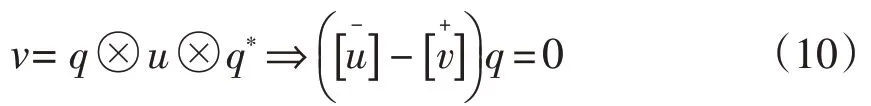
根据式（1）可知：

根据式（10）和式（4）得到对应的K矩阵：

2 基于比力方程的QUEST算法

为了解决陀螺仪测量值同时包含晃动角速度和地球自转角速度的问题，对姿态变换矩阵C nb进行链式分解，将晃动问题转化为载体系的运动问题，并通过陀螺仪的输出进行求解。

首先，分解姿态变换矩阵，将t时刻的姿态变换矩阵(t)分解为初始0时刻的姿态变换矩阵(0)，0-t时刻的导航系变化以及0-t时刻的载体系变化。

其中载体系的变化可以通过陀螺仪的输出得到，其中×为的对称矩阵：

导航系的变化可以通过地球自转角速度和对准时间得到，其中×为的反对称矩阵：

通过矩阵的链式分解将(t)的求解转化为(0)的求解。

导航系下的比力方程为：

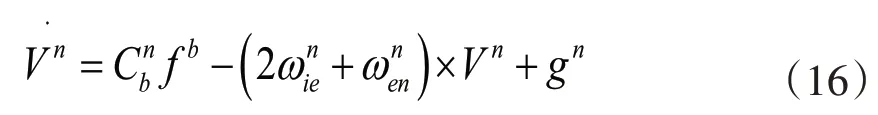
其中Vn为导航系下的速度，f b为惯性元件测得的比力，ωnie为导航系下地球自转角速度，ωnen为导航系相对于地心坐标系的角速度。gn为导航系下的重力加速度。根据式（13）的链式分解得到：

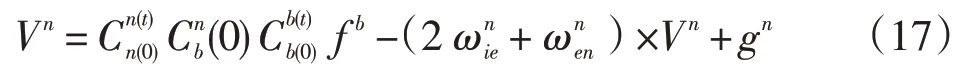
式两端左乘矩阵得到：

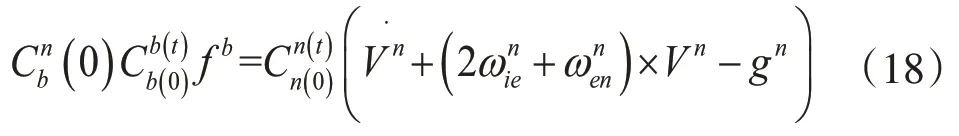
对两侧积分得到：

其中：

可以将求解过程转化为Wahba问题［10］，对比式（11），其中(0)等价于R，βv等价于vi，αv等价于ui。当惯性元件原地晃动时，可认为Vn，Vn(0)为0，并忽略高阶小量×Vn可将βv进行化简：

根据式（4），可将αv和βv作为QUEST算法中更新K矩阵的两个观测矢量。

3 仿真结果

3.1 仿真环境假设

根据韩勇强［7］研究中舰船在风浪下的晃动情况，对人体发射状态的晃动情况进行模拟。相比舰船而言，人体的晃动频率更高，晃动幅度较小。仿真设定如下：

（1）假设弹体的俯仰角θ，横滚角γ和航向角ψ做周期性变化。

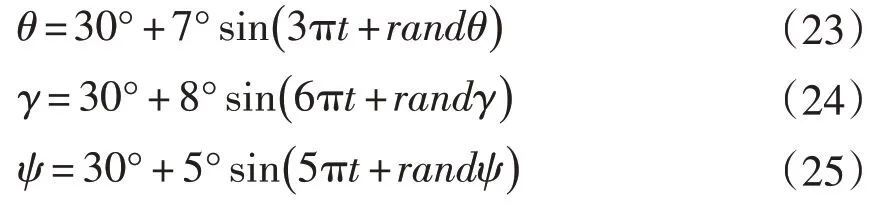
其中randθ，randγ，randφ是[ ]0,2π上的任意值。

（2）假设由身体起伏会造成微幅线位移，其中位移频率参考人体呼吸时的频率。

其中i=x，y，z。Ax=0.03 m，Ay=0.03 m，Az=0.04 m。fx=1.5 Hz，fy=2 Hz，fz=3 Hz，φ为随时间变化的[0 ,2π]上均匀分布的随机相位。

（3）惯性元件本身的误差和漂移。以ADIS16470惯性元件为例，根据元器件手册选取比较重要的4个特性，误差大小如表1所示。

表1 惯性元件误差

得到三轴陀螺仪输出和加速度计0～15 s局部时间内输出如图1所示，其中左侧一列为陀螺仪的输出，右侧一列为加速度计的输出。可以看出陀螺仪的输出由于姿态角的变化呈周期性变化，加速度计的输出由于不规则的线位移运动呈现出无规则变化。

图1 三轴加速度计与陀螺仪的输出

3.2 仿真结果分析

设定仿真时间为300 s，采用QUEST算法在人体晃动的仿真条件下进行初始对准，得到的对准误差及收敛趋势如图2～图4所示。

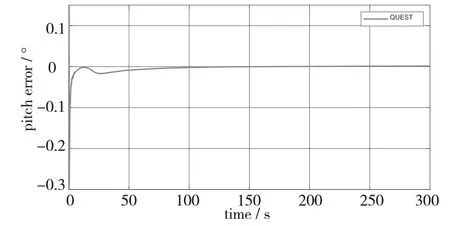
图2 俯仰角误差

图3 横滚角误差

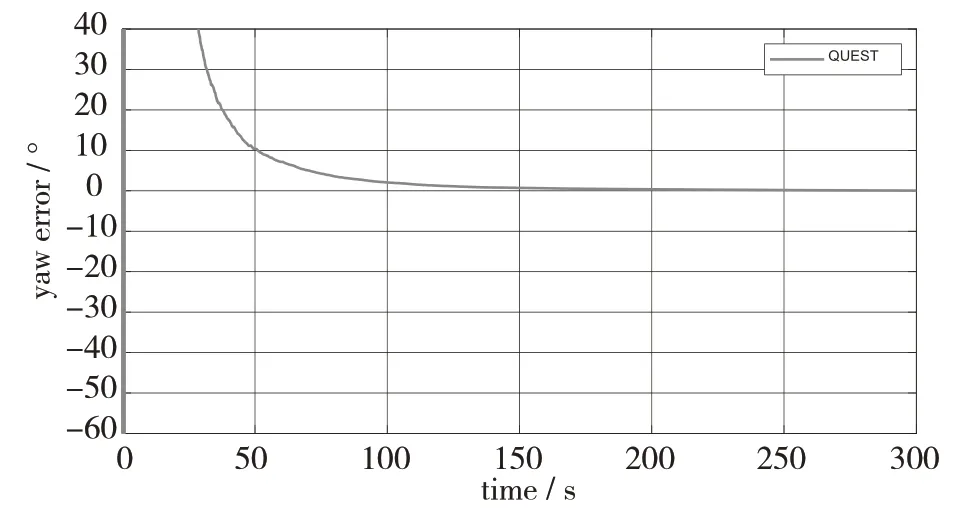
图4 航向角误差

由图2～图4可知，对于QUEST算法来说，其俯仰角和横滚角的对准精度大致相同，且远高于航向角的对准精度。即横滚角和俯仰角在满足一定精度条件下实现短时间的快速对准，而航向角则需要采取其他方式实现快速对准。

为了防止单次仿真的偶然性，采用50次蒙特卡罗试验，分别记录在10，100和300 s情况下的俯仰角、横滚角和航向角的误差。误差均值和标准差如表2所示。

从图5～图7和表2中可以看出，随着对准时间的增加，姿态角的误差方差逐渐减小。在10 s的求解时间内，QUEST算法的俯仰角误差和横滚角误差可以控制在±6′以内，但10 s内航向角误差过大，需要更长的时间才能够收敛。

表2 姿态角误差均值与标准差统计

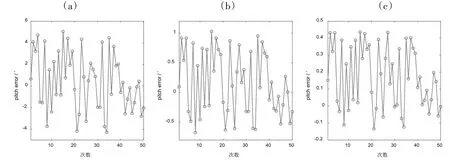
图5 俯仰角蒙特卡罗试验结果

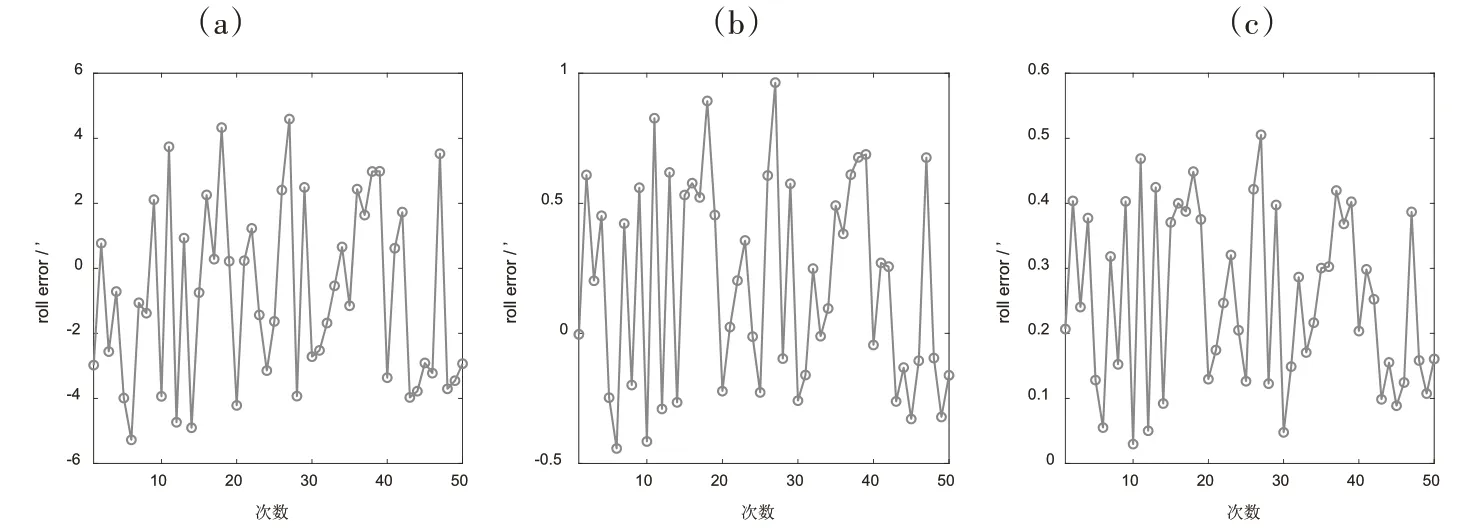
图6 横滚角蒙特卡罗试验结果

图7 航向角蒙特卡罗试验结果

设某单兵火箭弹的初始速度为150 m/s，初始俯仰角为20°，初始航向角为60°，根据弹道方程求解出理想弹道。在初始条件中加入俯仰角和横滚角的误差，实际俯仰角横滚角误差小于0.1°，实际航向角误差小于0.8°，再根据弹道方程得到实际弹道数据。比较实际弹道和理想弹道，发现在10 s的飞行时间1400 m射程上由姿态角造成的位置误差为0.48 m＜0.5 m，满足实际要求。

4 结论

针对单兵肩扛式火箭弹快速初始对准问题，本文对人体晃动的环境进行了模拟，推导QUEST算法的求解过程。通过对仿真结果的分析可以看出，QUEST算法可以实现俯仰角和横滚角在10 s内快速对准，在多次蒙特卡罗试验中，误差值可以保证在±6′，均方根误差在2.8′（1σ）以内，航向角可以实现300 s内对准，误差值为±48′，均方根误差小于5.6′（1σ）。在弹道仿真的情况下，QUEST算法可以实现1400 m射程上位置误差小于0.5 m，满足实际打击需求，后续应进一步进行试验验证。