基于K近邻改进算法的城市配送量预测研究

肖 赟，刘 洋，裴爱晖，梁子君

（1.合肥学院 城市建设与交通学院，合肥 210601；2.安徽省智慧交通大数据分析与应用工程实验室，合肥 210601；3.交通运输部公路科学研究院，北京 100088）

城市配送是指服务于城区及近郊的货物配送活动，它是物流链条中“最后一公里”的配送，在整个供应链环节内起着重要的起承转合作用。近年来，随着国内商品经济空前繁荣，互联网技术及电子商务的崛起，我国同城货运市场规模不断扩大，城市内部的各种货物流通需求日益高涨［1］。2020年我国同城货运市场规模达到14 245亿元［2］。城市拥堵、城市污染、配送成本不经济等现象成为城市配送发展瓶颈［3］。与此同时，城市配送需求的小批量、多品种、高频次、时效性强的直接配送、住宅配送以及“门到门”配送需求日益增长［4］，对目前的城市配送平台和交通管理部门提出更高的要求。

需求预测是优化城市配送资源的重要内容。2021年交通运输部、公安部、商务部三部委在推进城市绿色货运配送示范工程建设中，提出“重点分析论述城市货运配送面临的新形势及需求特征”。订单量是城市配送优化的基础，李建斌等［5］基于城市配送平台订单数据，研究了其与车辆匹配优化策略；赵泉午等［6］基于订单量，进行城市配送网络优化研究。针对城市配送特性准确预测城市配送的订单需求量，进而科学分配城市配送资源，对缓解城市拥堵和污染程度，提升配送服务质量，创建城市绿色货运配送示范工程有着重要的意义。

国内外学者提出较多数学预测模型方法，如时间序列法、历史平均模型、回归预测法［7］及卡尔曼滤波法［8］等。部分学者改进了上述传统数学预测模型，Williams［9］提出季节性ARIMA模型，分析结果在统计上要优于多元回归的方法。聂佩林等［10］提出的基于约束卡尔曼滤波的短时交通流量组合预测模型，其得出的预测结果优于或持平其他单一预测模型。张晓利等［11］为提高交通流预测的准确性，提出改进的非参数回归方法并应用于交通流预测。Yu Wei等［12］提出EMD-BPN混合方法在预测地铁短期客流方面表现良好且稳定。李高盛等［13］基于LSTM的神经网络模型，对多个站点上下车客流量的长时间序列数据进行学习，结果表明同时进行多站点客流量的学习能够提高预测结果的准确度。郑为中［14］提出贝叶斯组合神经网络模型，并将其应用于短期交通流量的预测取得较好的预测效果。韩春颖等［15］将稀疏高斯过程混合（SGPM）模型用于短时交通流预测，研究结果表明，基于新算法的SGPM模型不仅能够分模态展示预测结果、输出置信区间，且短时交通流预测均方误差小于4.8%。

随着非参数回归模型在预测领域的兴起，以K近邻算法为代表的预测方法开始引入到交通预测领域，其算法思路主要为：找到K个和当前状态向量最相似的历史状态向量，并对历史状态向量加权计算后，预测当前状态相关数值。Smith团队［16］通过同一个历史数据集，分别采用时间序列模型、K近邻算法和神经网络模型进行预测，发现K近邻方法稳定性和误差精度均最好。K近邻方法核心问题有三个：一是对历史数据集进行分类，即识别历史数据不同模式；二是构建状态向量，在交通领域往往将历史时刻交通数据划分成若干个样本，每一个样本则是一个状态向量；三是确定K值算法。

历史数据集分类研究方面，刘钊等［17］将美国波特兰快速路历史路口交通量数据集作为一个整体，并未按时间或空间分布进行分类。林培群等［18］对广州南站地铁进站客流量分为10种日客流发展模式，但预测时仍采用全天历史数据集。王翔等［19］认为通过整体历史数据集中搜索最近邻的方式，预测只能采用一个K值，当数据波动较大或者遇到交通突发状态时，将明显降低预测的准确性，由此他对沪宁高速公路上海——南京方向的行程时间进行了分析，根据高速公路流量变化，将历史数据集分为早高峰、晚高峰、平峰期等类别，并分别进行行程时间预测，但其对历史数据的分类主要依据高速流量波形图主观判断，缺乏对数据分类的科学性校验分析。

状态向量用于描述不同时刻的比较标准，由于交通量或客运量具有时间序列的自相关性，很多学者选择预测时刻前T时刻数据作为状态向量。对于T的选值，大多学者主要依据时间自然周期进行划分，如预测某一个小时的交通量，一般以日为单位，将前23个小时交通量作为状态向量；预测某一天的交通数据，则以周为单位，将前6天交通数据作为状态向量［20］，这种方式在部分预测领域容易导致较大误差。部分学者注意到T值的选取与预测精度存在很大关系，通过相关系数选择T值，但相关系数ρ与T值之间的关系缺乏深入研究［19］。Porwik P等［21］发现“近邻”总是出现在一个相对较窄的时间段内，绝大多数情况下T小于10个时间周期，但并未提出具体T值的计算方法。王雪菲等［22］通过遍历可能的T值，提出了一种基于预测误差最小的T值选择方法，具有较大的借鉴意义。

K值的选择研究理论比较丰富，周小鹏等［23］认为交通流量的随机性太强，由此提出将K的个数根据不同模式确定不同取值，进而优化预测精度；于滨等［24］认为K值满足期望值后，可以取较小的K值，以提高计算速度。涂锐等［25］在预测城市路段行程时间研究中，通过选取K的最小值和最大值，在K取值区间内采用交叉验证的方法，比较预测精度确定最优K值。林川［26］预测机场客流量时，预先设定一个K值范围，然后对比每个K值的预测结果，选取误差最小的K值作为最终K值。以上学者从不同角度对K值计算提出了不同方式，但其主要核心基本保持一致，即：通过设定K值取值范围，并确定预测精度的评价方法，遍历所有K值，以预测精度最高或预测精度达到某一个阈值为目标，确定最优K值。

现有的研究对城市配送订单预测提供了很好的方法借鉴，但也存在一些不足，由于城市配送订单量变化的复杂性、不确定性，参数回归模型等部分在长期预测领域表现较好的模型方法，在预测延迟、突变方面暴露出较大的不足；而现有的K近邻方法中历史数据集分类、状态向量选择还存在着优化空间。针对这些问题，本文以预测城市配送日订单量为目标，首先按照以日为单位，对数据集分为N类；其次状态向量维度T从1～N-1分别取值，计算不同取值下的预测误差，与此同时针对每一个T值，遍历K可能取值范围，进而找到预测精度最高的T值和K值；最后，比较不同预测方法的误差，以校验研究方法的科学性和可行性。

1 基于K近邻模式的城市配送平台订单预测研究方法

1.1 K近邻算法基本思想

K近邻算法（K-Nearest Neighbor）是非参数回归方法中最常用的算法之一，在特征空间中，如果一个样本附近的K个最近样本的大多数属于某一个类别，则该样本也属于这个类别。该算法近年来已广泛应用于分类、回归和模式适配等领域［27］。基于K近邻改进算法构建的城市配送共享平台订单预测模型的算法基本流程如下：

（1）对历史订单原始数据库进行清洗，以7天为时间周期，构建订单数据集，并建立标准化数据结构；

（2）以状态向量、距离度量方式和近邻个数K等要素构成模型的搜索机制，确定状态向量T以及近邻个数K的取值；

（3）确定K近邻预测算法，计算预测结果；

（4）以平均绝对百分比误差（MAPE）为指标评估预测结果，并进行比较分析。

算法流程图如下图1所示。

图1 K近邻算法基本流程

1.2 历史数据集的分类

城市配送数据以日为单位统计了城市配送订单量，为此本文以周为单位将数据分成若干组数据集，并分析每周的日订单变化趋势。根据订单变化规律，对历史数据进行分类。一般而言，预测精度将随着数据分类的增加而增加。考虑到城市配送数据组中只有7天数据，数据维度相对较少，可以将数据分为7类，即周一、周二、周三、周四、周五、周六和周日。

1.3 状态向量的确定

状态向量是当前数据与历史数据比较的标准，一般选取与预测对象最为相关的因素，来平衡预测精度和运行时间两者的要求［24］。本文研究的是城市配送订单需求预测，结合城市配送的运行特性，预测周的每日数据能充分体现订单需求量的变化趋势，因此通过观察历史数据库中订单量的变化规律以此构建状态向量：

式中：n表示第n周，n取0时表示预测周当周；xn（T-1）为预测周前的第n周第T-1天的城市配送订单量，因为T必须小于数据组的维度7，所以T的取值范围为［1，6］，为了寻求最佳的T值，本文拟以预测精度最高为目标，遍历所有T值。

1.4 距离度量方式

距离度量方式是用于度量历史数据库中各个历史样本与当前数据的近似程度，当K近邻非参数回归用于短时交通流的预测时，通常采用的是欧式距离作为度量指标：

式中：dn为历史状态向量与当前状态向量之间的距离；xni为预测周前第n周第i天的历史城市配送订单量；x0i为预测周前第i天的城市配送订单量；T的取值范围为［1，6］。

1.5 评价方法

常用的评价模型指标有平均绝对误差（MAE）、均方误差（MSE）、平均绝对百分比误差（MAPE）与均方百分比误差（MSPE）［18，27］。MAPE在其它评价指标的基础上进行了标准化处理，更直观地反映本模型的预测精度和差值，具有较好的适应性，由此本文以平均绝对百分比误差（MAPE）指标作为模型的性能评价指标，MAPE越小表示预测精度越高，模型越好。其计算公式如下：

式中n为样本数；xi为样本实际值；为样本预测值。

1.6 预测算法

预测算法是用于描述如何利用搜索到的K个近邻数据预测下一天的配送需求量：

式中：x^0为当天数据预测值；xi为历史数据库中搜索到的第i个邻近所对应的订单量；di为当前向量与第i个邻近点的距离。

1.7 自适应K值和T值的标定

如何选择合理的K值和T值，是预测模型的关键［24］。通过对预测情景进行分类，对每类计算不同K值和T值下的预测结果的误差变化率，并进行预测精度比较，选择较优的数值。

步骤1：对预测场景进行分类，预测值分为N类，设N=Ni，Ni∈[1 ,7]。

步骤2：场景Ni下确定状态向量T的取值，设T=Ti，Ti∈[1 ,6]。

步骤3：设K=Kj，Kj∈[1 ,Kmax]，Kmax取值根据历史数据量进行综合确定。

步骤4：选择历史数据集的任意1周We作为测试数据集，其他n-1周作为训练数据集，其中每个数据集有7个数据，分别代表一周7天的城市配送订单量。

步骤5：计算Ti和Kj下的测试数据集We平均绝对误差百分比。

步骤6：计算Ti和Kj下的所有测试数据集We平均绝对误差百分比。

步骤7：当MAPE取得最小值时，所预测对应的Ti和Kj就是预测场景下数据集最优值。

部分代码如下：

将历史数据划分为训练集Train和测试集Test；

定义预测函数Predict（历史数据，种类）：

T取值1到Ntype（种类数-1）：

K取值1到Nhist（经验值）：

KNN算法预测Test测试集的预测值

计算此次预测误差MAPE

遍历完成后记录最低误差MAPE对应的T值和K值

对预测数据种类Ni进行遍历：

应用函数Predict计算并记录每个Ni对应的T值和K值，并记录相应最小误差MAPE；输出：

不同种类Ni数据对应的最佳T值和K值；

不同种类Ni预测误差MAPE随T值和K值的变化趋势数据。

2 城市配送共享订单预测实例与分析

2.1 研究数据

选取合肥市某城市配送共享平台2018年1月1日至2020年12月31日的订单数据作为预测研究的数据。

原始订单数据主要包括日期、行政区、活跃车辆数、运输趟次、接单量及完单量等，原始数据信息见表1。

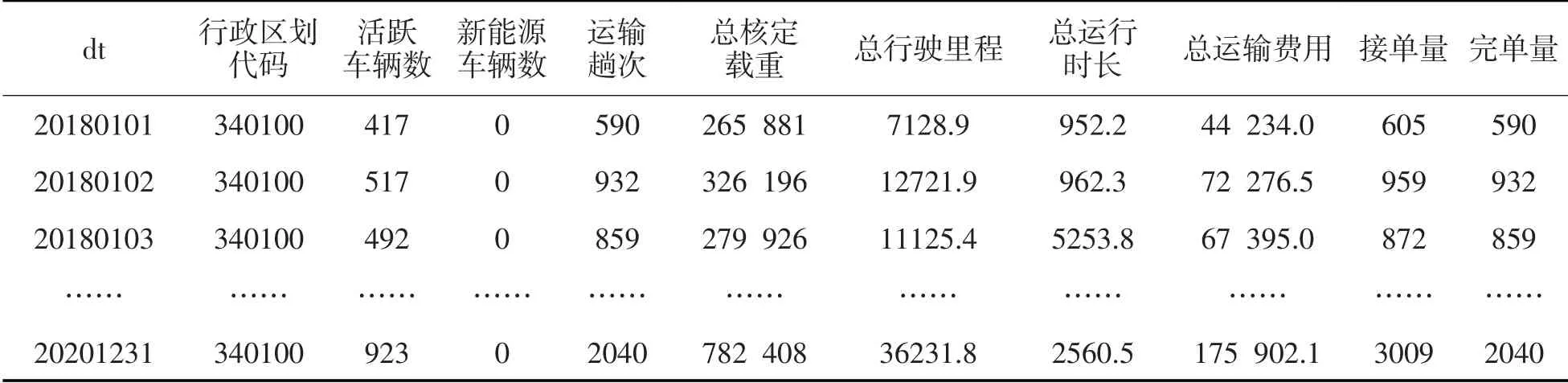
表1 原始数据

由于原始数据不满足直接分析的条件，需要进行预处理并将其转化为标准化数据。首先，对原始订单数据中存在空值和异常值等情况进行删除或均值化处理；其次，基于研究目的去掉无关字段，仅保留订单量列和时间列；再次，考虑到2020年初疫情期间的数据差异性较大，去掉疫情期间的订单异常值；最后，结合城市配送特性和短时交通流的预测方法，将原始数据转化为标准时间序列以便后期分析。

具体处理数据流程如下所示：

（1）读取历史原始数据；

（2）将含时间信息的字符串转成时间戳；

（3）根据时间戳划分为周次；

（4）转成以周为时间序列的数据集；

（5）删除含空值及异常值的时间序列；

（6）删除低于或高于平均值50%以上的时间序列数据；

（7）删除受疫情影响较大的时间序列；

处理过后的标准实验数据共143周订单量数据，见表2。

表2 标准化实验数据样本

2.2 构建状态向量

状态向量的合理构造是影响预测精度的重要因素［28］。本文不同于部分学者［18，25］将状态向量的数据维度T设定为固定值，而是采取变化的T个时间段流量数据作为状态向量。状态向量维度T从1～N-1分别取值，如周日的状态向量T取值可为1～6，即周日的状态向量根据T的取值分别为（T6），（T6，T5），（T6，T5，T4），（T6，T5，T4，T3），（T6，T5，T4，T3，T2），（T6，T5，T4，T3，T2，T1），周六的状态向量根据T的取值分别为（T5），（T5，T4），（T5，T4，T3），（T5，T4，T3，T2），（T5，T4，T3，T2，T1），（T5，T4，T3，T2，T1，T7），Ti代表周i，以此类推。

2.3 K值和T值的选择

K值过大或过小都不利于提高预测精度，算法遍历过程中KMax值过大将导致计算时间过长，效率太低，KMax取值一般为总体数据样本的20%～40%［18-20］，由此确定KMax=30。

当T=1时，状态向量只有一个值，搜寻数据集个数为1，基于标准化143周数据，采用自适应K值算法，从第一周开始，第一周作为测试集，剩余142周作为训练集，计算出T=1时，第一周测试集中，每天K=1至K=30的相应的MAPE；然后第二周作为测试集，剩余142周作为训练集，同样计算出在T=1时，每天K=1至K=30的相应的MAPE，重复上述步骤，直至143周数据全都遍历，由公式（3）得出143周所有数据在T=1情况下的预测精度，并分别统计出143周中每周一至周日的平均预测精度。

当T=2时，状态向量有2个值，搜寻数据集个数为2，基于标准化143周数据，采用自适应K值算法，重复上述步骤，得出143周所有数据在T=2情况下的预测精度，并分别统计出143周中每周一至周日的平均预测精度。

再依次类推分别计算得出T=3至T=6情况下每天相应的平均预测精度，结果如图2所示。

图2 各日预测精度瀑布图

由图2可知，周四、周五的平均预测精度高，不同T值下的平均误差在6.5%以内，周一及周日的预测精度相对较差，不同T值下的平均误差在11%左右。整体上，T值处于1～4时预测精度相对较高。

对历史数据集分为周一至周日共七类，以相应的最小误差值为优化目标，确定出7类数据集相应最佳K值与T值，如下表3所示。

表3 各日最佳K值与T值

由表3可知周一至周日七类数据的最佳K值均为2，表现出趋同性。但最佳T值在1～4之间波动，各数据分类（周一至周日）的最小误差均在12.5%以内，周三的预测误差最小（2.18%），周二和周四的预测误差较低（5.83%，5.02%），周一、周六和周日的误差在10%左右。整体预测精度较好。

2.4 预测结果比较分析

为更好地比较不同方法的预测效果，采用K近邻算法对2020年12月21日至2020年12月27日城市配送数据（测试集）进行预测，将剩余142周历史数据作为训练集，得出相应的预测精度，并利用历史平均模型及移动平均算法对同一目标时间段进行预测。预测效果如图3所示，预测方法的性能指标如表4所示。

图3 2020年12月21日至2020年12月27日城市配送订单量预测结果对比

表4 3种预测方法的MAPE值

由图3及表4可见，三种预测方法的预测误差有较大的差异，K近邻算法预测误差最小（8.34%），其次移动平均算法（11.16%），历史平均模型误差较大（23.65%）。预测结果说明历史平均模型虽然能在一定程度范围内反映城市配送订单量的大概变化趋势，但其未能反映数据的不均匀性与非线性特性，在预测中无法应付突发事件的数据情况，其预测值与实际值存在非常大的差异。相较于历史平均模型，移动平均算法整体预测值与实际值更为接近。移动平均算法虽在个别预测中误差较小，但未能充分反映城市配送订单量的变化趋势，其预测效果与实际值的变化趋势存在明显的差异，预测稳定性不高。对比移动平均算法，K近邻算法的整体误差更小，预测曲线与实际值较为吻合，在预测精度和把握变化趋势方面表现更好。

综上，K近邻算法的预测精度最高，具有更强的自适应能力，可随着预测环境情况的变化，通过对历史数据集的分类、搜索算法和相关参数的调整，采取相适应的T值与K值，能够较为精准地预测城市配送订单量，具有较好的适用性和实时性。

3 结语

以合肥市城市配送共享平台为研究对象，对其2018-2020年订单历史数据进行标准化处理，以周为数据集单位，对数据集划分为七类。针对城市配送订单需求短时预测，构建自适应K近邻模式预测模型，以平均绝对百分比误差最小为目标，优化了参数K和T的取值，能够有效降低预测误差。

实例数据分析表明，K近邻模式的城市配送订单预测模型、历史平均模型和移动平均算法的平均绝对百分比误差分别为8.34%、23.65%、11.16%，K近邻预测模型整体预测精度为91.7%，优于其他两种预测算法，且预测曲线与实际变化趋势更吻合，更适用于复杂突变的数据预测。本研究对于精确化分析城市配送订单需求，进而优化城市配送资源和运营方案有着重要的意义。下一步，可结合地理信息系统和车辆位置信息，对其流量流向分布进行更深层次的挖掘分析。