电磁-永磁式强非线性吸振器的减振性能研究

唐明君，陈建恩，陆文星，杜锦龙

（1.天津理工大学 机械工程学院 天津市先进机电系统设计与智能控制实验室，天津 300384；2.天津理工大学 机电工程国家级实验教学示范中心，天津 300384）

振动问题广泛存在于航空航天、汽车、土木等诸多工程领域中，在绝大多数情况下振动会对结构产生危害，长期以来振动抑制都是学术研究的热点问题。阻尼减振技术是目前发展比较完备的技术之一，该技术通过附加阻尼的方式将振动能量转化为内能，并以热量的形式耗散。阻尼减振技术不改变原有的结构，可靠性高，因此得到广泛的应用。

吸振器的概念最早由Frahm[1]提出并应用于振动控制领域。吸振器通常是由单个质量元件、弹簧元件和阻尼元件构成[2]，可以有效抑制主结构的振动。但其只有在吸振器固有频率处才能发挥较好的减振效果。在此基础上，Roberson[3]在吸振器中引入非线性，有效提升了吸振器的有效振动抑制的带宽和鲁棒性。

非线性吸振器主要可以分为刚度非线性和阻尼非线性两种，其中刚度非线性吸振器在近年来发展非常迅速。刚度非线性吸振器的研究包括对立方刚度吸振器[4]、分段线性刚度吸振器[5]、可变刚度吸振器[6]等的研究。此外，一些学者研究了同时具有刚度非线性和阻尼非线性的吸振器[7]。

电磁力研究目前在电机[8]、电磁继电器[9]、电磁斥力装置[10]以及主动式电磁作动器[11]等领域得到了广泛研究。电磁斥力机构具有结构简单、动作速度快，可靠性高等优点[12]。董润鹏等[13]利用电磁斥力设计了一种中压直流混合型断路器用四触头并联高速斥力机构。肖帅飞[14]对单体电磁永磁混合结构排斥力的性能进行了研究。孙志卓等[15]提出一个新的物理量即电磁弹簧，具体地讨论了电磁弹簧形成原理并推导出了其数学表达式，并以电磁弹簧为理论基础设计出了一种固有频率可调的电磁式吸振器。诸多学者的研究结果以及大量的实验数据表明电磁-永磁斥力机构具有极其特殊的非线性动力学性能。

本文基于电磁和永磁装置设计出一种新型的强非线性吸振器。研究了电磁-永磁非线性吸振器的宽频减振性能，分析了连接该吸振器的线性主振子的频率响应特征，研究了电磁铁和永磁铁的间距对减振性能的影响。

1 非线性吸振器模型

单自由度主振子和由电磁-永磁斥力结构构成的强非线性吸振器所组成的系统如图1所示，由牛顿第二定律可得该耦合系统在简谐激励下的动力学方程：

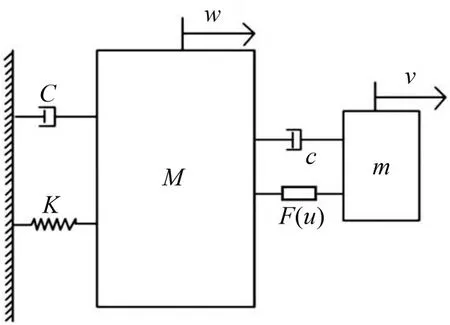
图1 动力学模型

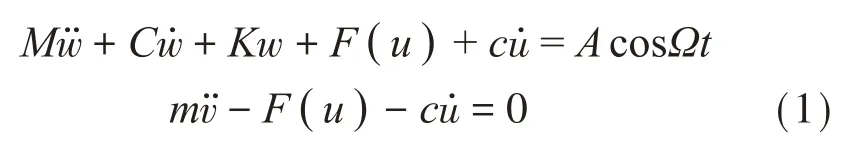
w和v表示主振子和吸振器的位移，其中u=wv，C与c分别表示主振子与吸振器的阻尼系数，K为主振子的刚度。A表示简谐激励幅值，Ω表示简谐激励频率。M为主振子的质量，m表示吸振器的质量。

F(u)为电磁结构中的电磁斥力，如图2所示。该结构中部为永磁体动子，两侧为电磁线圈组成的定子，永磁体动子可以在中间导轨上左右移动。根据Inoue[16]等的研究，永磁体动子受到单组电磁定子的斥力大小为：

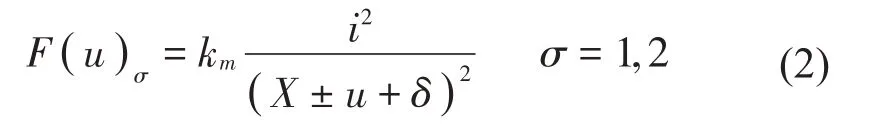
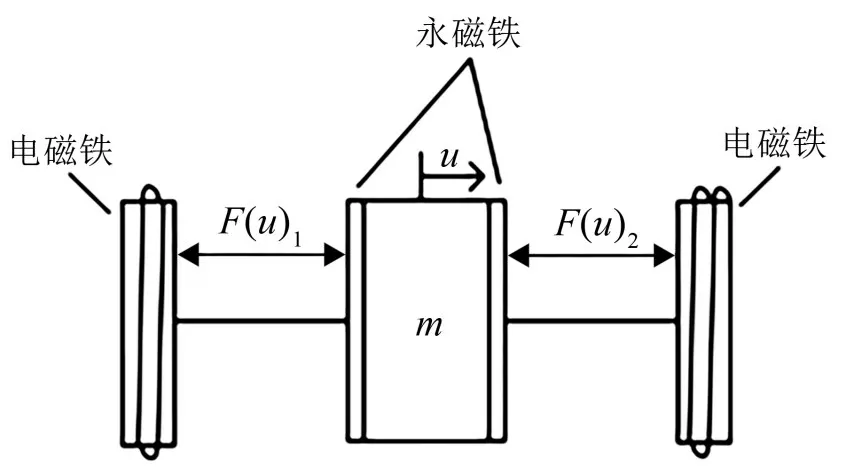
图2 电磁-永磁非线性吸振器结构示意图

其中：X表示永磁体动子与单个电磁铁定子之间的初始距离，由吸振器结构所决定，故为固定值。u表示主振子与吸振器之间的相对距离。km和δ为Inoue等研究中通过实验测得的数据。通过借鉴文献中的实验数据，这里km的取值为73.241 Nmm2/A2，δ=0.882 mm，在电流i取1.45 安培时，kmi2为150 Nmm2，代入到式(3)得到方程式(3)：

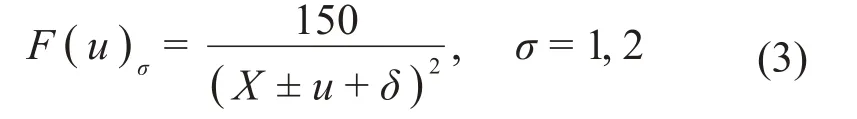
由于永磁体动子平衡位置在导轨中间，当动子受激励向某一侧运动时，会改变动子与两个定子之间的距离，两个电磁定子均会对动子产生电磁斥力作用，则两组电磁-永磁斥力机构中电磁定子对永磁体动子产生的斥力分别为：

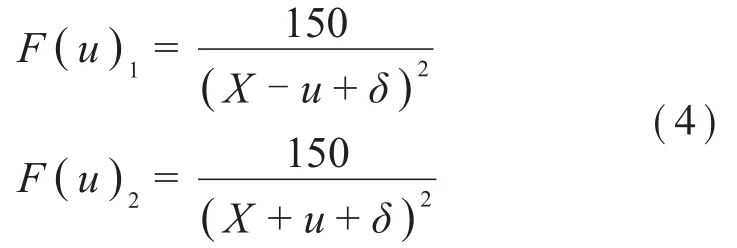
其合力为：

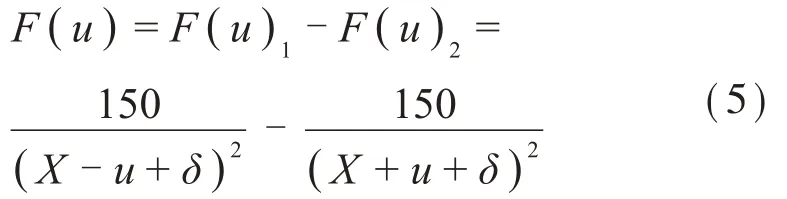
将式(5)代入到式(1)得到：

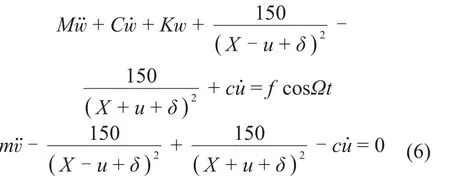
由式(5)可以得出如图3所示的曲线。从图像可以看出，电磁-永磁结构的力学特性曲线具有中间平缓、两端陡峭的强非线性特征。

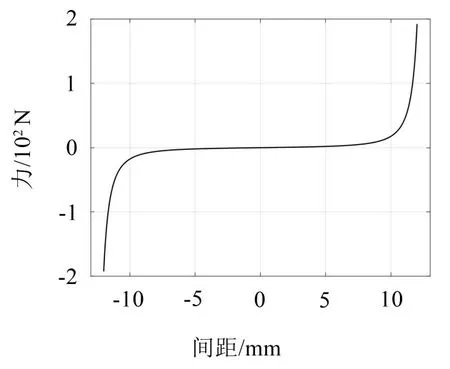
图3 电磁-永磁结构的力学特性曲线

2 减振性能仿真研究

使用4阶龙格库塔法对系统动力学方程进行数值求解，系统的各项参数如下：

M=100 kg，m=10 kg，C=4 N/(m/s)，X=12 mm

c=0.1 N/(m/s)，K=40 000 N/m，δ=0.882 mm

首先使用A=1 N 的简谐激振力对系统进行激励，得到连接与未连接吸振器状态下的主振子频响曲线，如图4所示。连接吸振器后主振子在固有频率处振幅降低至40%左右，并且连接吸振器的主振子固有频率相较于未连接吸振器的主振子固有频率偏移量非常小。图4(a)显示吸振器与主振子的相对位移在Ω=5.4和Ω=20.2处有两个幅值。

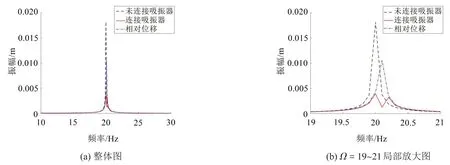
图4 K=40 000 N/m，A=1N时的频率响应曲线

为探明响应出现的原因，用最小二乘法将式(5)拟合成多项式函数：

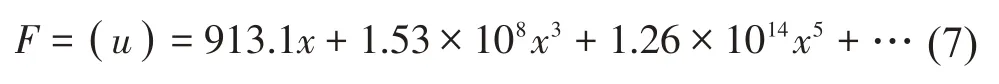
其中式(7)线性刚度系数、立方刚度系数、五次方刚度系数的单位分别为N/m、N/m3、N/m5，由式(7)可以得出该吸振器的非线性回复力仍具有线性部分，因此连接该吸振器的主振子理应同时具有两个幅值。而图4(a)显示主振子连接吸振器后，只在Ω=20.2处存在一个较高幅值，这得益于电磁-永磁机构特殊的非线性力学性能。

为研究该吸振器的宽频减振能力，改变主振子的刚度，令K1=10 000 N/m，K2=90 000 N/m，吸振器的各参数保持不变。同样使用幅值A=1 N简谐激振对两个系统进行激励，得到连接与未连接吸振器状态下的主振子频响曲线分别如图5和图6所示，K1=10 000 N/m的主振子在固有频率处幅值可以降低至20%左右，但是K2=90 000 N/m的主振子在固有频率处振幅可以降低至无吸振器时的45%左右。对比之前K=40 000 N/m 时主振子幅值在固有频率处降低至40%左右可以看出：该吸振器对于不同刚度的主振子均有减振效果。由于相同激励下主振子固有频率越小，其振幅越大，故主振子刚度越低，吸振器的效果越能得到更好体现。

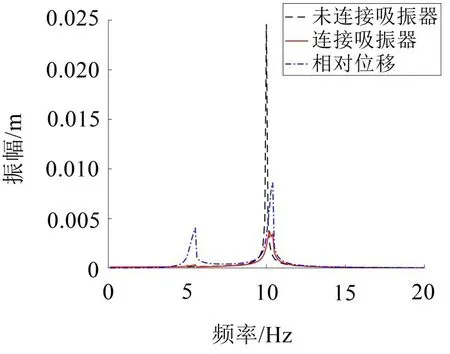
图5 K1=10 000 N/m时的频率响应曲线

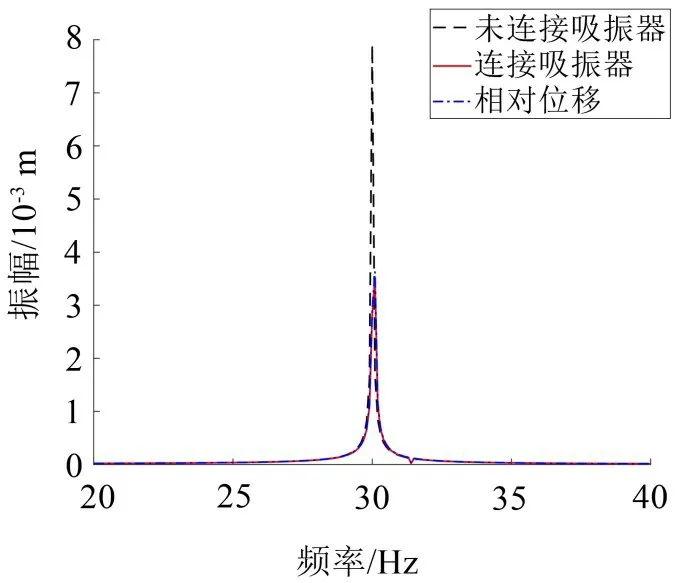
图6 K1=90 000 N/m时的频率响应曲线

改变激振力的幅值A，研究在不同的简谐激振幅值下该吸振器的减振性能。现在选用参数为M=100 kg、K=40 000 N/m的主振子，使用简谐激励幅值A=0.5 N 和A=1.5 N 的简谐激振力对系统进行激励，分别得到如图7(a)和图7(b)所示的频率响应曲线。从结果中可以看出简谐激振幅值A=1.5 N时吸振器仍具有良好的减振性能，但是简谐激振幅值A=0.5 N时吸振器却几乎没有减振性能。出现这种现象的原因是该非线性吸振器在一定的激励幅值下才会被激活。从能量传递角度来说，靶向能量传递存在一个阈值，若激励能量太小会使靶向能量传递无法进行，即非线性吸振器不被激活，虽然非线性吸振器可在较宽的共振频带内进行吸振，但系统内的能量转移只有在一定的激励幅值范围内才能够高效地完成。相关问题国内外诸多学者已经做出研究[17－19]，本文不再赘述。根据图3中的曲线可以看出，此时永磁体动子受到两侧电磁铁产生的电磁斥力的合力F(u)很小，因此当简谐激振幅值较小时，吸振器的减振性能没有被完全激发出来。

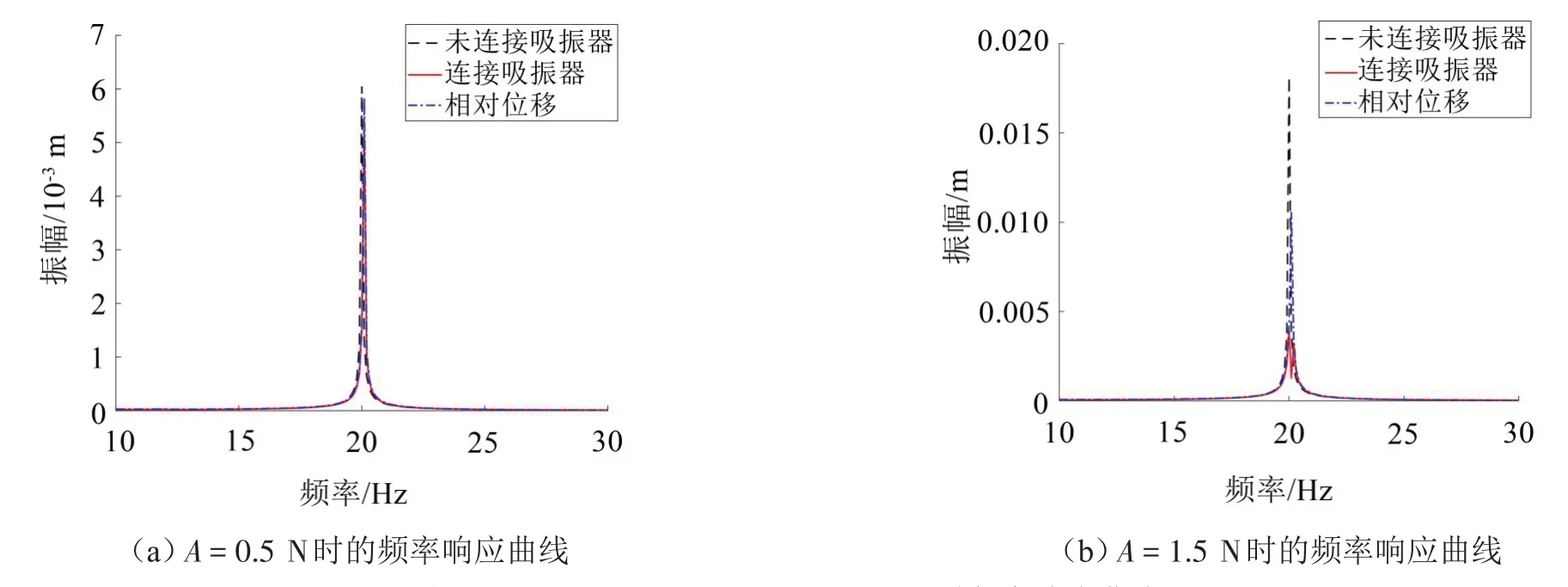
图7 K=4 000 N/m、A=0.5 N和A=1.5 N时频率响应曲线

在简谐激振幅值A=0.5 N 时，电磁-永磁吸振器的永磁动子在距离中间位置很近的范围内运动，导致减振性能很低。可以推断出吸振器减振性能与简谐激振幅值A和永磁动子与电磁定子之间的距离X有关。仍然选用刚度K=40 000 N/m的主振子，在其他参数均相同的情况下，分别获得动子与定子之间的间距分别为X=14 mm、X=16 mm、X=18 mm、X=20 mm 时，简谐激振力幅值A从1 N 到2 N 变化过程中电磁-永磁吸振器的减振性能曲线如图8所示。

从图8中可以看出，间距越小则减振性能越好，并且随着力的增加，不同间距条件下减振性能都会有所提升。由图8还可以看出，间距越大时，随着简谐激振力幅值A增大，吸振器的减振性能增加越快。

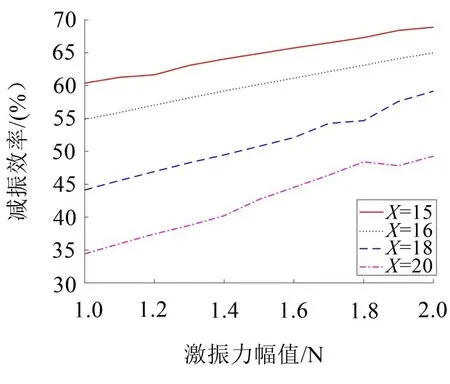
图8 不同间距下减振性能与激振幅值的关系

但是，考虑到吸振器工作过程中永磁动子不能与电磁定子相撞，因此也不能仅通过减小间距来提高减振性能，应根据具体的减振对象，考虑间距的大小。

3 结语

本文设计一种新型的具有特殊非线性特征的电磁-永磁式吸振器。建立了含电磁-永磁非线性吸振器系统的动力学方程，并通过龙格库塔法对其进行了数值分析。

将吸振器连接不同刚度的主振子后进行仿真，证明电磁-永磁式非线性吸振器具有良好的宽频减振性能。此外，由于电磁-永磁斥力机构的特殊非线性力学性能，连接吸振器的主振子频率响应曲线只出现一个较高峰值，这有利于对被减振结构的保护，而吸振器则会出现两个较高的峰值。

此外，吸振器具有激活阈值，只有在简谐激振力幅值达到该值以后才能够具有良好的减振性能。在一定范围内，随着简谐激振幅值增加，吸振器的减振效果会随之增强。并且，适当减小电磁铁和永磁铁的间距，可以增强减振效果。