基于负电阻电磁分流阻尼的结构振动控制
2022-08-19毛崎波
李 戈,毛崎波,王 永
(1.南昌航空大学 飞行器工程学院,南昌 330063;2.国网上海市电力公司 特高压换流站分公司,上海 201413)
将电磁分流阻尼(electromagnetic shunt damper,EMSD)用于结构振动控制是一种新发展起来的被动控制方法,具有控制力和阻尼力较大、信号响应为宽频、传递力具有非接触性等优点。EMSD 的原理是利用线圈与永磁体的相对运动所产生的电磁阻尼力[1]阻碍系统的振动,并通过外接的分流电路消耗或者收集由系统的机械能转化而来的电能。
根据机电类比,当把LRC 2 阶串并联电路作为EMSD 的分流电路时,可以将EMSD 视作一个参数可以方便调节的调谐质量阻尼器[2]。而对于参数可调的EMSD 来说,重要的是得到分流电路的最优设计值,其次是使得分流电路参数达到或者接近对应的最优值。但是对于一个附加EMSD的单自由度系统而言,线圈的直流电阻往往要大于分流电路最优电阻值,因此可以在分流电路中接入负电阻模拟电路中和线圈直流电阻,从而使得分流电路等效电阻接近于最优电阻,进而提高振动控制效果。Yan等[3]提出在一种电磁调谐质量阻尼器的分流电路中接入负电感负电阻电路,并将其用于悬臂梁的多模态控制;Zhang等[4]在EMSD 的L-R型分流电路中接入负电阻电路,并将其用于悬臂板的多模态振动控制(结构的固有频率较低,在100 Hz以内);郑文广等[5]提出在分流电路接入负电阻来调节接入EMSD后的结构固有频率,并取得了极好的控制效果。以上几位学者的研究均表明将负电阻电路用于结构振动控制有着非常好的效果,但其均应用L-R 型分流电路,L-R型分流电路具有感抗会随频率增加的缺点,而不能用于控制高频振动,而且,即便能用于控制结构的多模态振动,也只是在结构固有频率较小的情况下。但是考虑到在LRC串联的2阶振荡电路中感抗与容抗相位相差180°的特点,将L-R 电路改为LRC 电路可以消除分流电路中的高频感抗,进而能更有效地控制结构振动。同样,采用LRC分流的EMSD的参数优化也是至关重要的。Zhou等[7]先后使用了定点理论、H2优化、最大衰减系数优化(极点配置法)等3种方法,得到了附加EMSD 的单自由度系统在做简谐、随机、瞬态等3 种振动时,接入负电阻后的LRC串联分流电路的最优参数解析解。Inoue等[8]在假设线圈电感值为给定值条件下,利用定点理论推导出将分流电路为LRC 串联电路的EMSD 用于无阻尼单自由度系统的振动控制时,分流电路的最优设计参数。然而对于定点理论来说,若主系统存在阻尼系数时,不同阻尼比所对应的频响函数曲线并不会交于两个定点,此时定点理论会面临失效[9]。且文献[7]中机电耦合系数被限制为2 以内,根据定点理论所推导出的结论才能成立,这是其不足之处。对于与文献[8]同样的模型,Tang等[10]利用H2优化推导出了最优调谐比、阻尼比的解析表达式,从其结论来看,主系统无阻尼时,采用LRC串联分流的EMSD的机电耦合系数被限制为2 以内,更进一步地,Ikegame等[2]利用H2优化理论得到了有阻尼时主系统最优调谐比、阻尼比的解析表达式,但是通过计算其结论可知:主系统有阻尼时,采用LRC 串联分流的EMSD 的机电耦合系数将会小于0~2 中的某个数,比如当主系统的阻尼比为0.05 时,机电耦合系数被限制为1.709 9 之内,而且当主系统阻尼比越大,机电耦合系数被限制得更加严重。而且,如果实际的机电耦合系数接近于这些上限值,会使得调谐比趋近于0,从而导致最优电容变得非常大,因此采用H2优化和定点理论的方案可行性不足。从这些优化EMSD 分流电路的参数的文献来看,使得衰减系数最大化的极点配置法的结论,对机电耦合系数的大小没有任何限制,且其计算过程也相对简单,因此其适用性是最好的。
因此本文选择文献[2]中推导出的极点配置法的结论确定EMSD 的LRC 分流电路的最优设计参数,并接入负电阻电路,用于对悬臂梁进行结构振动控制,然后通过计算频响函数,判断接入负电阻后的控制效果是否能得到提升。
需要注意的是,因为实验难度较大,且目前并没有国内外学者针对采用负电阻LRC 分流的EMSD进行过实验,因此本文仅涉及理论模型和数值计算。
1 LRC 串联分流的电磁分流阻尼用于悬臂梁的振动控制
图1所示即为EMSD控制悬臂梁结构振动的示意图,其中坐标系原点在固定端处,传感器的测量点和激振器的激励点位于同一位置,即xs=x0,设电磁线圈的放置点为xi,则电磁线圈对悬臂梁施加的作用力可以等效为线圈的中心点位置xi处的集中力;其中Rsh为分流电路电阻,Rsh可以为负电阻即Rsh=Rn。
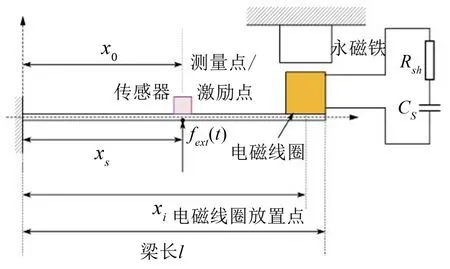
图1 LRC串联的电磁分流阻尼用于悬臂梁振动控制的示意图
图2所示为加入负电阻后分流电路的等效电路图,其中eM=为感应电动势,电阻R0为线圈直流电阻,Rsh为分流电路外接等效电阻Rsh=R1-RSRb/Ra,若Rsh为负电阻,可以令Rsh=Rn,Rn为负电阻。
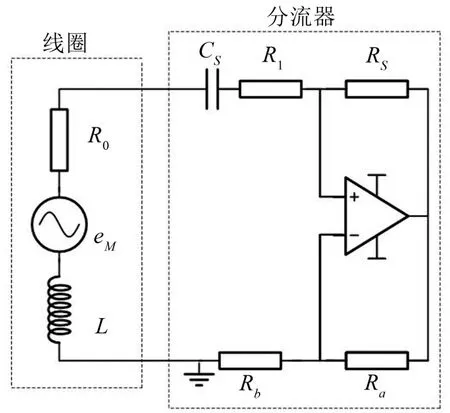
图2 由电磁线圈、电容和负电阻分流器组成的电路示意图
假设悬臂梁的弯曲振动的模态函数为ψi(x)(数学表达式见参考文献[11]),则悬臂梁的第i阶模态质量和模态阻尼、模态刚度矩阵如式(1)、式(2)、式(3)所示[11]:
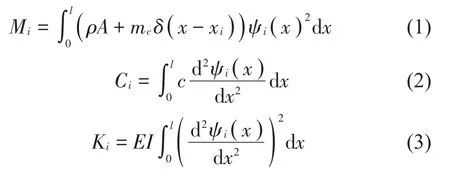
假设电流为i(t),激振力的大小为f(t),则第i阶的模态力为如式(11)所示[11]:
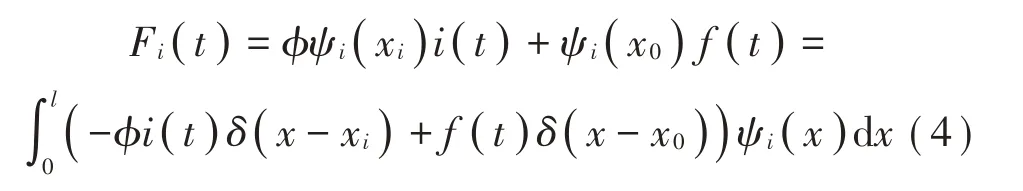
设悬臂梁的第i阶模态坐标为Wi,则点x处的位移为式(5)为将EMSD 用于悬臂梁振动控制时的机电耦合方程,其中R为等效电阻:
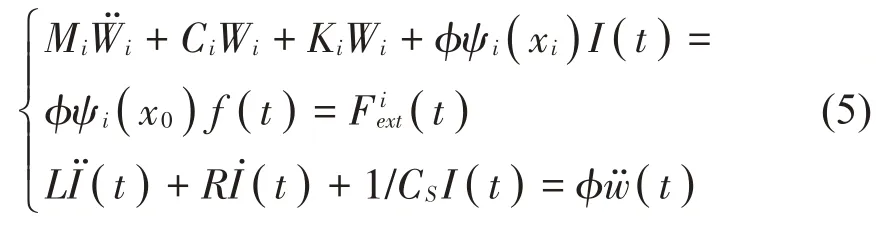
根据模态叠加法,可以将上述方程改写如式(6)所示:
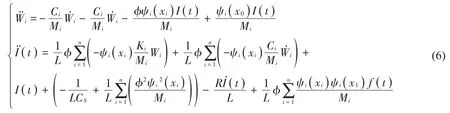
假设以激振力f(t)为输入量,测量点速度Vx0为输出量,则状态空间模型如式(7)、式(8)所示:
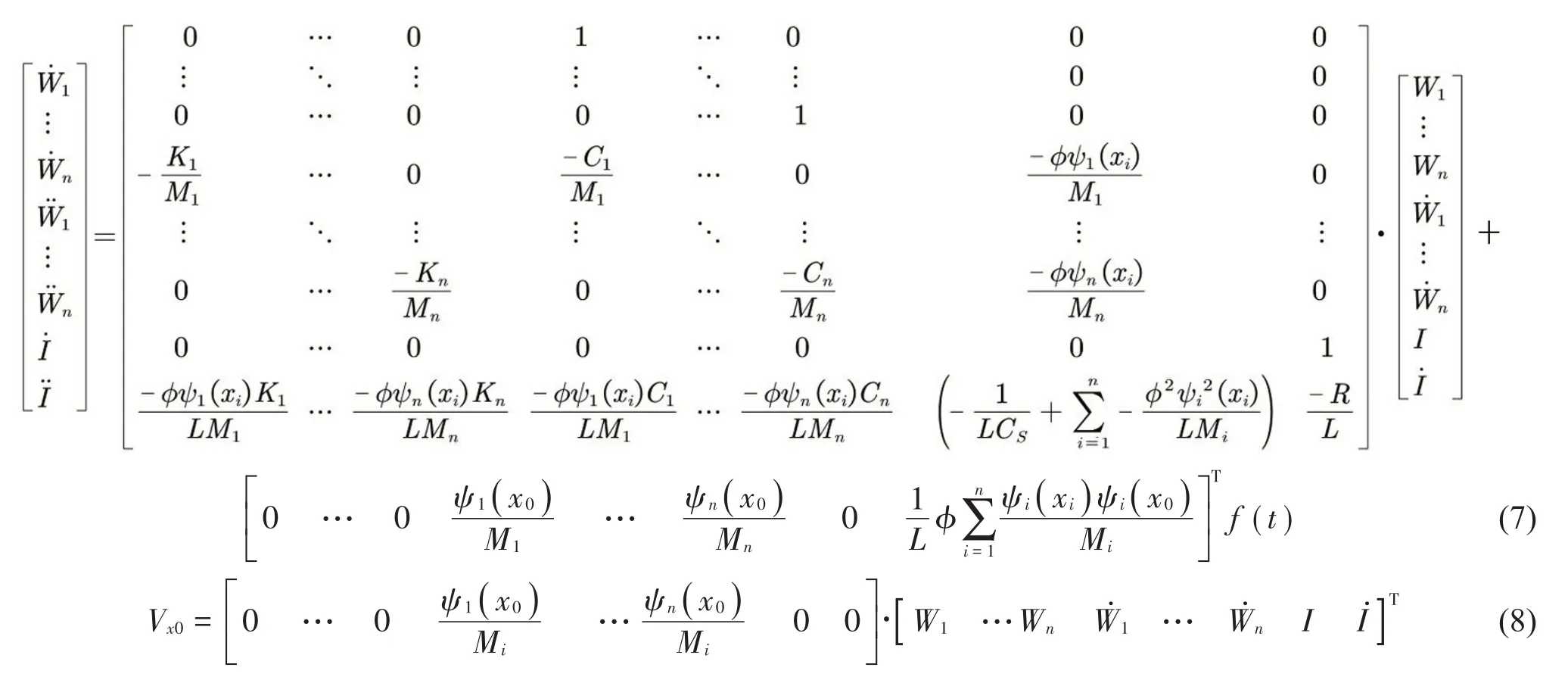
2 数值计算
将采用LRC 分流的EMSD 用于控制悬臂梁的振动,所涉及到的悬臂梁的参数以及电磁线圈参数如表1所示。
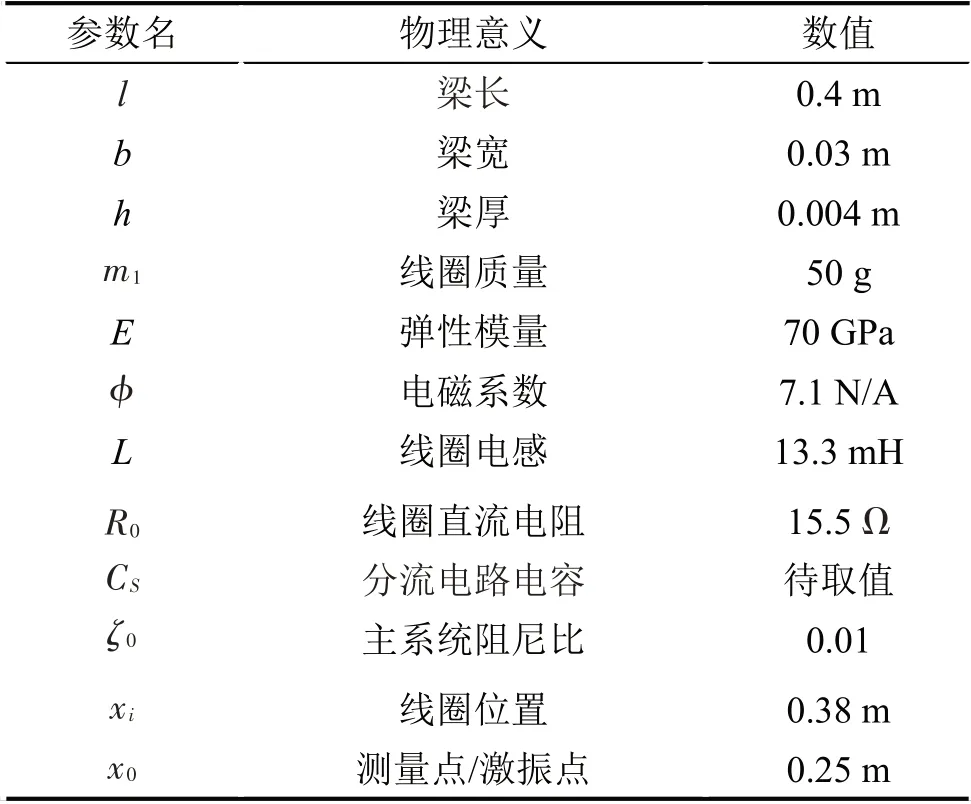
表1 悬臂梁以及线圈参数
悬臂梁的多个固有频率ωn1至ωnN对应的分流电路最优电容为CS1至CnN。根据文献[2],选用极点配置优化法时,对于控制悬臂梁的第i阶模态振动,分流电路的最优调谐比为由此得到控制悬臂梁第i阶模态振动的分流电路最优电容为最优电阻阻值为Ropti=结构的前4阶的固有频率以及最优电容的数值如表2所示。
结合第1节所推导出的状态空间模型和表1、表2的数据,算得在不同负电阻下采用LRC串联的电磁分流阻尼控制的悬臂梁第1阶模态振动速度频响函数如图3所示。

表2 结构固有频率以及最优电容的数值
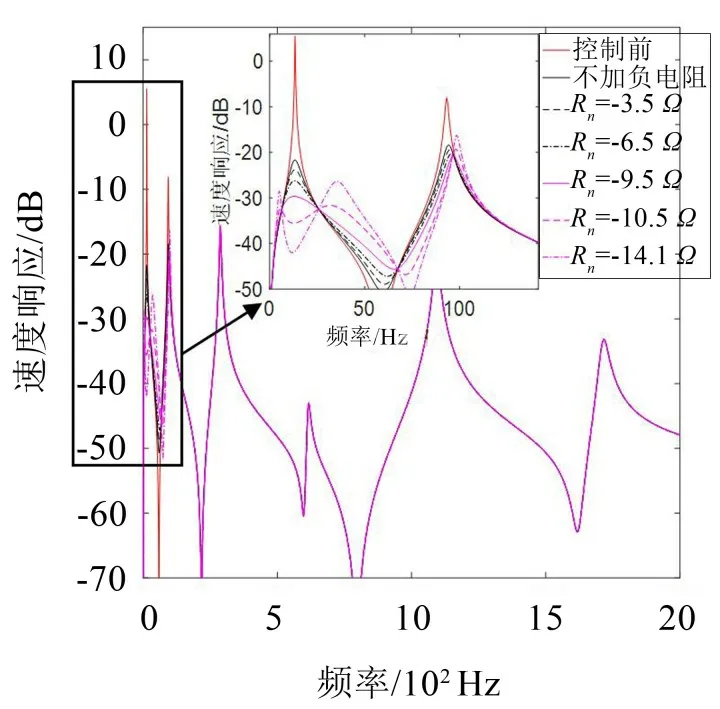
图3 将采用LRC串联的电磁分流阻尼用于悬臂梁的振动控制(控制第1阶模态振动)
由图3可知,逐步增加负电阻后,控制效果也随之逐步提升,但需要注意的是,并不是负电阻越大,控制效果越好,这是因为将EMSD用于结构振动控制时,其相当于一个虚拟的调谐质量阻尼器,当负电阻增大并使得等效电阻接近于0时分流电路阻尼比会趋于0,从而控制效果也会下降;控制第1 阶模态振动所对应的分流电路参数也会对第2阶模态振动有影响,因此电磁分流阻尼具有多模态控制效果。
但这种控制效果在结构固有频率较高时会消失,比如对悬臂梁第3 阶模态振动几乎没有控制效果,产生这种现象的原因是:对于控制悬臂梁第1阶模态振动的分流电路的电路原件,若不改变其数值大小,直接将其用于控制第2阶模态振动,此时分流电路的振荡频率为结构的第2 阶固有频率,此时线圈上的感抗远大于电容上的容抗,分流电路产生失谐,导致电流急剧降低及线圈发出的控制力大大降低。这也第2 阶模态的控制效果没有第1 阶模态好的原因。由于第3阶及更高阶模态的固有频率远大于第1 阶模态的固有频率,若结构以这种高阶模态的固有频率振动,则线圈的感抗愈加增大,容抗愈加趋近于零,从而产生了更加严重的失谐,这也是其对第3阶及更高阶的模态几乎没有控制效果的原因。
需要注意的是,图3中的第2阶模态振动的频响函数在负电阻取-9.5 Ω 至0时的幅值要小于不加入负电阻时的幅值,这说明了负电阻能在一定程度上提升EMSD的多模态控制效果。
图4所示为控制第1 阶模态振动时的相频响应曲线。
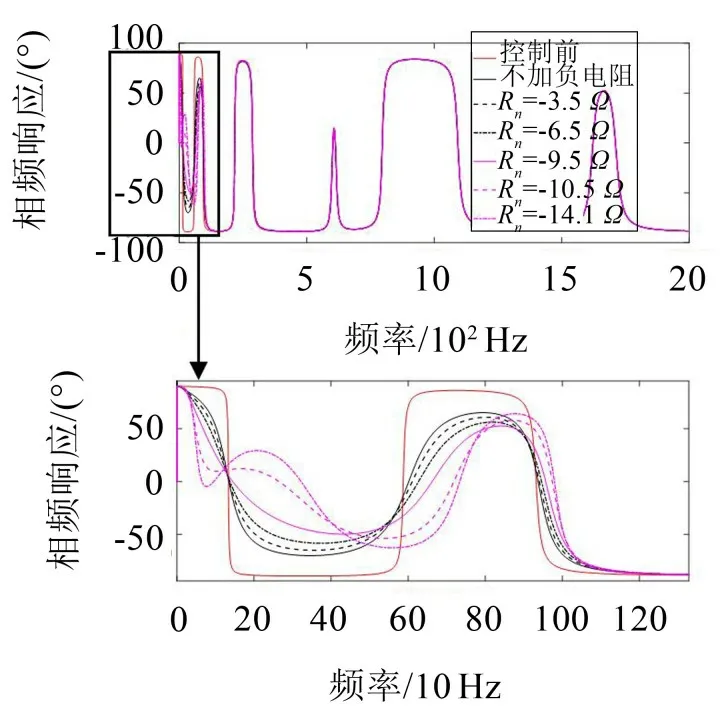
图4 相频响应曲线(控制悬臂梁第1阶模态)
由图4可知,相频响应曲线在每个固有频率处均出现一个180°的相位滞后,而且在每个虚的零点通过一个180°的相位超前得到补偿。相位总是在90°至-90°之间振荡,这是由于传递函数的零点和极点相间排列所导致的。
分别将分流电路电容取CS2、CS3、CS4,并将它们代入式(7)、式(8),计算出在分流电路接入不同负电阻条件下采用极点配置法优化悬臂梁第2 阶、第3阶、第4阶模态振动时的频响函数,如图5所示。
由图5可知,在分流电路中接入负电阻能很好地提高电磁分流阻尼的控制效果;且只需要更改电容数值,LRC 串联分流电路就能控制结构的任一模态振动,也包括固有频率较高的模态。这是L-R 型负电阻分流电路所不及的。
根据文献[2],在图5的(a)至(c)图中,最优电阻阻值逐次增大,因此最优负电阻的阻值大小随着模态阶数递增而减小。图5(a)至图5(c)中,对于各阶模态的调控对邻阶模态没有产生控制效果,这是因为单独控制第2阶至4阶模态中的任一阶振动,意味着分流电路的参数与被控制的那一阶模态对应,且分流电路处于谐振状态,若结构以相邻模态的固有频率振动,由于相邻模态固有频率的数值相差足够大(见表2),分流电路会产生严重的失谐,导致等效阻抗急剧增大,使得电流和控制力都会急剧降低。这是相邻模态所受到的影响很小的原因,同时也是结构固有频率较高时EMSD 不再具有多模态控制效果的原因。
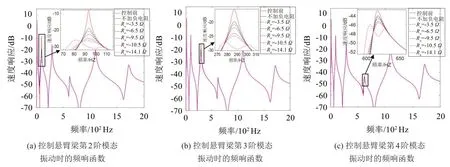
图5 采用LRC串联分流的电磁分流阻尼分别控制悬臂梁的第2阶至第4阶模态振动
3 结语
本文建立了将采用LRC 串连分流的电磁分流阻尼用于悬臂梁结构振动控制的状态空间模型,数值计算结果表明了以下结论:
(1)负电阻通过降低分流电路电阻,增大电流和控制力,能有效地控制结构振动。
(2)当结构固有频率较低时,电磁分流阻尼具有多模态控制效果,且负电阻能在一定程度上提升这种多模态控制效果。
(3)LRC分流电路相比于L-R分流电路,只需要更改分流电路参数就能控制结构的其他模态振动,这是其优势所在。
