斜坡基桩水平动力响应解析解
2022-08-19张玲岳梢刘亚楠彭文哲
张玲,岳梢†,刘亚楠,彭文哲
(1.湖南大学土木工程学院,湖南长沙 410082;2.建筑安全与节能教育部重点实验室(湖南大学),湖南长沙 410082;3.国家级建筑安全与环境国际联合研究中心(湖南大学),湖南长沙 410082)
随着跨江、跨沟谷等斜坡地形上的高速公路建设的不断推进,斜坡桩基工程越来越多.斜坡基桩不仅要承受上部结构自重等竖向荷载,还要承担车辆制动等水平动荷载作用.与平地基桩相比,因斜坡岩土体应力场分布不对称,斜坡基桩桩-土耦合振动问题以及侧向承载能力设计计算更加复杂.因此,分析水平动荷载作用下斜坡基桩的动力响应具有重要的意义.
目前,国内外已有学者针对水平静载下斜坡基桩的受力变形分析开展了一些研究.试验方面,赵明华等[1]通过现场试验探究了陡坡段双桩基础承载特性及荷载传递机理,为同类工程设计施工提供了有效参考;尹平保等[2]通过室内模型试验研究了坡度等因素对斜坡段基桩的斜坡空间效应的影响;杨明辉等[3]基于室内模型试验指出了桩前土抗力折减效应与坡角及临坡距紧密相关.数值模拟方面,Georgiadis 等[4]采用三维有限元软件研究了边坡桩基的水平承载性能,并得到了考虑坡角的p-y曲线表达式;Ng等[5]基于有限元软件,研究了水平荷载下斜坡套筒桩的受力变形,得到了套管对斜坡桩性能影响规律.理论计算方面,赵明华等[6]和杨超炜等[7]根据m法假定,分别提出陡坡段双桩内力计算有限差分解及有限杆单元解;尹平保等[8]假定桩后边坡趋于稳定,产生的水平推力甚小,只考虑桩前土抗力作用,提出了基于p-y曲线法的斜坡段基桩内力变形计算方法;杨明辉等[9]基于斜坡基桩横向加载破坏试验,提出考虑陡坡效应的应变楔计算方法,并研究了陡坡效应的影响范围;Peng 等[10-11]假定斜坡地基桩前浅层土难以提供土抗力,提出修正应变楔理论;我国《公路桥涵地基与基础设计规范》(JTG 3363—2019)[12]建议采用m法计算平地桩身内力变形,对于斜坡地形可将地基反力系数比例系数m值折减一半简化计算.上述研究采用不同方式均对桩前土抗力进行折减以考虑斜坡效应,且取得较好的效果,但均属于静力学范畴,斜坡段基桩的动力响应计算方法鲜有报道,尚缺乏系统深入的研究.
现有水平动力响应方面的研究主要是针对平地基桩开展的.早期有学者采用动力Winkler地基梁模型[13-15]将桩周土模拟为弹簧和阻尼器,该模型虽简单直观,但不能很好地反映桩土相互作用,忽略了桩周土的连续性;Nogami 等[16]和Novak 等[17]考虑土体应力的梯度变化,将土体视为三维连续介质,通过构造势函数解耦土体三维波动方程,求得桩周土水平振动阻力,根据桩土相互作用得到桩基水平振动响应解析解;Zheng 等[18]将此扩展到大直径管桩,推导了黏弹性土层中大直径管桩水平动力响应的解析解;栾鲁宝等[19]考虑了竖向应力梯度变化和轴向荷载二阶效应的影响,研究了黏弹性土层中桩-土横向耦合振动问题;Hu 等[20]建立了径向非均质黏弹性土体的水平动力阻抗解析解;赵密等[21]考虑水-桩-土之间的耦合作用,建立了水中高桩水平振动响应解析解.以上研究对斜坡基桩振动响应有着一定的参考价值.
鉴于此,本文将在现有平地基桩水平动力响应理论的基础上,考虑斜坡效应,提出适用于斜坡段基桩的水平动力响应解析解,以期为斜坡基桩水平振动研究提供一定的理论参考.
1 计算模型建立及基本假定
1.1 计算模型
如图1 所示,斜坡段基桩桩顶同时受到水平简谐荷载Q0eiωt和摇摆简谐荷载M0eiωt作用;桩长为L,其中自由段长为L1,嵌入段深度为L2;桩径为Dp=2r0.假定桩前一定深度H0范围内的浅层土体难以提供水平抗力[10-11].实际计算土层厚度为H1,并设实际计算土层对应的桩轴中心处为坐标原点O,沿深度方向为z轴,水平方向为x轴.

图1 斜坡基桩计算模型简图Fig.1 Calculation model of pile in sloping ground
1.2 基本假定
为便于分析,根据图1 所示的简化计算模型,进一步做出如下假设:
1)桥梁基桩成桩后斜坡基本上趋于稳定,桩后岩土体产生的水平推力甚小,故可假定桩位处斜坡是稳定的,即不考虑斜坡的失稳破坏,也不考虑桩侧摩阻力及桩后土体水平推力的作用[8].
2)基桩视为线弹性Euler 杆件,忽略剪切变形及转动惯性,桩周土为各向同性黏弹性体[19,21].
3)桩土体系为小变形振动,桩-土体系接触良好,接触面不发生相对滑移,且只考虑水平方向位移,忽略竖向位移[19,21].
2 桩周土层水平振动
在水平简谐荷载作用下,桩-土体系处于简谐振动状态,相应的状态项均包含时间因子eiωt.为书写方便,在以下推导过程中均省略eiωt项.在对斜坡桩周土水平动反力推导时,先推导出平地基桩周土水平动反力,再进一步考虑斜坡的土抗力折减效应,最终得出斜坡基桩周土抗力表达式.
2.1 桩周土振动方程建立
当桩周土系统做水平振动时,根据黏弹性动力学理论,建立柱坐标系下桩周土运动方程如下:

式中:ur、uθ分别为桩周土的径向和环向位移;λs和μs为复拉梅常数,λs=2μsνs/(1-2νs),μs=Gs(1+2iξs),Gs为桩周土剪切模量,Gs=Es/(2(1+νs)),νs、Es、ξs分别为桩周土泊松比、弹性模量以及滞回阻尼比;ρs为桩周土密度.
2.2 桩周土边界及连续性条件
桩周土边界条件:

桩周土接触边界条件:

式中:up为桩身沿θ=0方向水平位移.
2.3 桩周土振动方程求解
引入势函数对土体振动控制方程进行解耦:
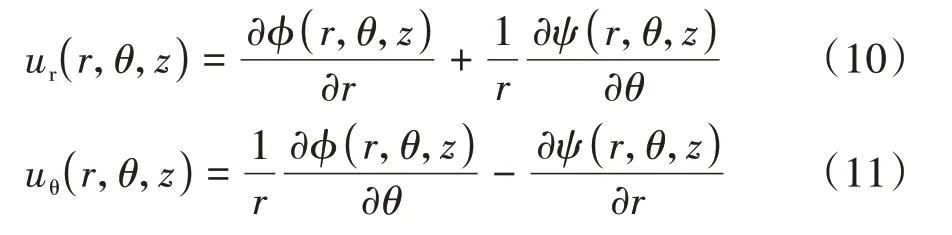
式中:ϕ(r,θ,z)、ψ(r,θ,z)为土体的位移势函数.
由式(10)(11)容易得到:
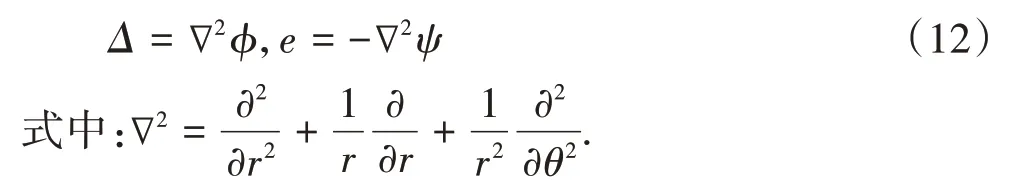
将式(10)~(12)代入方程(1)(2),化简得:


式中:A、B、C、D、E和F为待定系数;Kn1(·)和In1(·)分别为n1阶第一类和第二类修正Bessel函数.
势函数ϕ的解为:

同理,可得到势函数ψ的解:

根据式(7)并考虑修正Bessel 函数的性质,可得B=B0=0,n1=1.由式(8)(9)可知ur是θ的偶函数,uθ是θ的奇函数,可得C=D0=0.由式(5)(6)可得E=E0=0,gn=(2n-1)π/(2H1);n=1,2,3,….
因此可得:

式中:An、Bn为待定系数.
将式(26)(27)代入方程(8)(9)化简得:

由式(28)(29)得到:
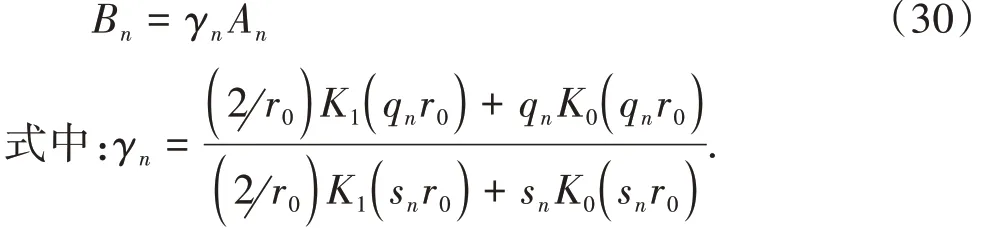
土层对桩的水平阻力p可表示为:

以上即得平地水平动反力p的表达式,但对于斜坡而言将会存在折减效应[8-9],《公路桥涵地基与基础设计规范》(JTG 3363—2019)[12]建议当桩基础侧面设有斜坡或台阶,且其坡度(横∶竖)或台阶总宽与深度之比大于1∶20 时,地基抗力比例系数m值应减小50%取用.即通过考虑土体强度折减来计算水平荷载下斜坡桩的受力变形,本文采用类似处理,对反力系数bn进行折减,引入折减因子ζ,ζ数值大小与边坡角度等紧密相关[2-4],例如:尹平保等[2]基于室内模型试验,提出不同坡度θs下基桩水平极限承载力的折减系数拟合式(1-θs/90°).
综上即得斜坡土层水平动反力ps:

3 单桩水平振动
根据假设1),可将图1 土层深度H0对应桩体划入自由段,并在下文求解中将自由段与土层深度H0对应桩体统称为自由段,相应的入土段则仅表示埋入土中实际计算土层对应桩体.
3.1 单桩振动方程建立
由动力平衡条件建立柱坐标系中桩运动方程.
自由段:
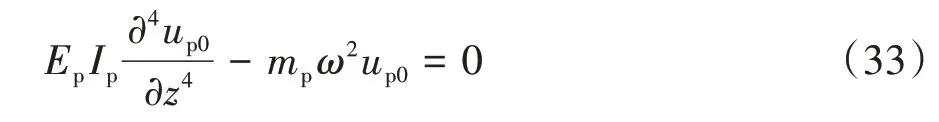
入土段:

式中:Ep为桩弹性模量;Ip为桩截面惯性矩;up0、up1分别为自由段、入土段的桩身水平位移;mp为桩单位长度质量,mp=ρpπr02,ρp为桩体密度.
3.2 单桩振动方程求解
3.2.1 自由段
令λ4=mpω2/(EpIp),可得式(33)的解为:

式中:C1、C2、C3、C4为待定常数.
由材料力学位移、转角、弯矩和剪力之间的关系可知:

式中:φp0、Mp0、Qp0分别为桩身自由段转角、弯矩和剪力;χ0为自由段系数矩阵.

则桩身自由段上、下两端的水平位移、转角、弯矩、剪力的关系可表示为:

3.2.2 入土段
式(34)由通解与特解两部分组成,容易得到式(34)的解为:

由桩周土接触边界条件式(8)(9)可得:
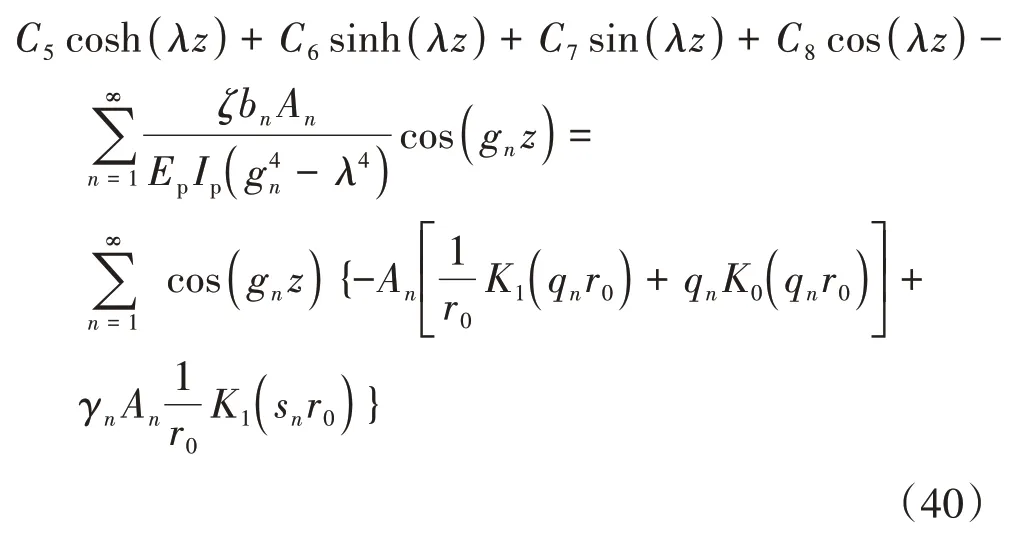
利用三角函数cos(gnz)正交性,式(40)两端同乘cos(gnz),在区间[0,L]上积分可得:

由式(41)可得:


将式(42)代入式(39)中可得斜坡基桩入土段水平位移up1解:


由材料力学位移、转角、弯矩和剪力之间的关系可得:

式中:φp1、Mp1、Qp1分别为桩身入土段转角、弯矩和剪力;χ1为入土段系数矩阵.

则入土桩段上、下两端的水平位移、转角、弯矩、剪力的关系可表示为:

结合式(38)和式(46),考虑桩身连续条件,可得桩底和桩顶的水平位移、转角、弯矩、剪力的关系为:

式中:fp=[χ1(H1)][χ1(0)]-1[χ0(0)][χ1(-L1-H0)]-1.
3.3 边界条件
Novak 等[17]给出了平地单桩桩端固定与铰接时的桩动力阻抗的解答,对于斜坡基桩而言,桩端一般嵌入基岩中,故本文给出式(48)桩端固定时的详细解答,铰接可类似得出.

桩顶已知边界条件:

限于篇幅,下文仅给出桩顶自由、桩端固定时的详细解答,其他边界条件可类似得出.
3.4 动力阻抗解答
结合边界条件式(48),由式(47)可得桩顶弯矩、剪力和桩顶水平位移、转角的关系:

式中:Kp为动力阻抗矩阵,其表达式为:

桩端铰接时的动力阻抗矩阵为:

根据动力阻抗的定义[15],可得单桩水平动力阻抗Kh、摇摆动力阻抗Kr以及水平-摇摆耦合动力阻抗Khr如下:

3.5 内力变形解答
结合边界条件式(48)(49),由式(47)可得桩顶水平位移、转角和桩顶弯矩、剪力的关系:
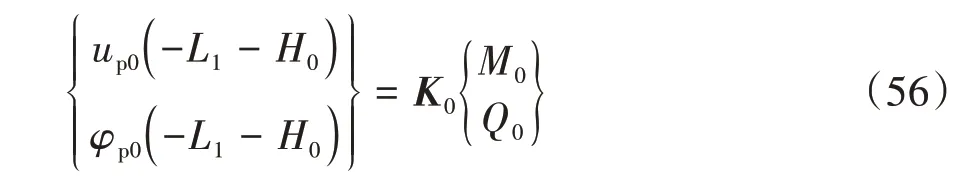
式中:K0为系数矩阵,其表达式为:

综上结合式(36)(44)即可得桩身内力变形解.
4 算例验证分析
因现有文献鲜有斜坡基桩水平动力试验或数值模拟报道,难以直接用对应试验结果验证本文解答正确性,故下文将分两步进行验证,其一是不考虑斜坡效应,将解答退化为平地基桩动力问题,并与已有平地动力解析解对比,验证桩周土振动方程以及基桩动力阻抗方程解答正确性;其二是不考虑水平动荷载的影响,将解答退化为斜坡基桩静力问题,与已有斜坡基桩静力数值试验对比,验证斜坡基桩水平振动响应解答的正确性.

4.1 算例1
为验证本文桩周土振动方程的正确性,本文与Nogami 等[16]理论解进行对比验证,基本参数为:r0/H1=100,νs=0.4,ξs=0.01,ζ=1,H0=0,L1=0,计算结果如图2 所示.图2 中土体第n振动模态阻抗因子βn=bn/ηs(第n模态下桩在发生单位水平位移时,对应土体在r=r0产生的水平阻力);an为土体第n阶固有频率,an=π(2n-1)/2,n=1,2,3,….图2 中横纵坐标分别为:无量纲土体频率a*=/a1(a1=π/2);无量纲土体阻抗因子=βn/(πμs)通常为复数,根据定义[16]实部为土体刚度虚部为阻尼.
由图2 可知,本文解与Nogami 理论解[16]吻合较好,表明本文桩周土振动方程是正确的.

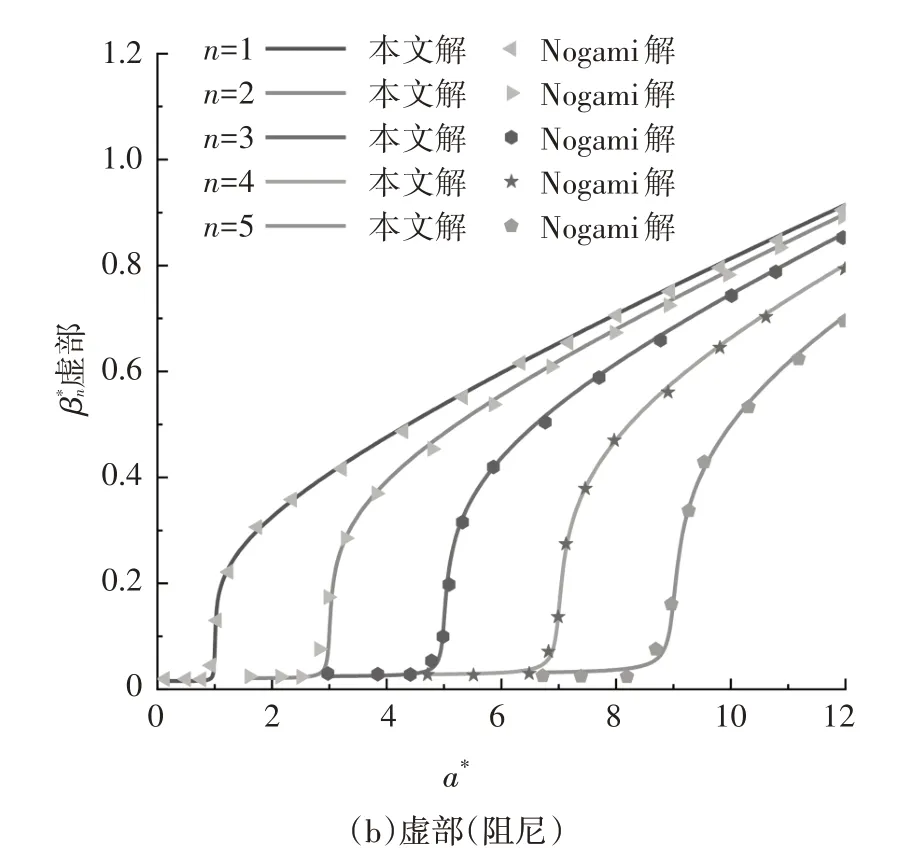
图2 不同振动模态n下,土体阻抗因子随频率a*的变化对比Fig.2 Comparison of soil resistance factor with frequency a*under different vibration modes n
4.2 算例2
为验证本文斜坡段基桩动力阻抗方程的正确性,令H0=0,L1=0,ζ=1,即退化为平地基桩动力阻抗解,与Chau 等[22]解析解进行验证.基本参数为:νs=0.4,ρs/ρp=0.6,L/r0=H1/r0=30,ξs=0.05,η′=0.01.边界条件为桩端铰接,计算结果如图3所示.图3中,横坐标为λ*/λ0,其中λ0为无土的独立弹性桩λ*的最小值,对于桩端铰接,Kh对应的λ0=1.571,其他边界条件取值见文献[22].纵坐标Kh′=Kh(动力)/Kh(静力),Kh(静力)可令ω→0,通过计算Kh(动力)的值确定.
由图3 可知,本文解与文献[22]解吻合较好,验证了本文动力阻抗方程以及相应程序的正确性.

图3 无量纲水平动力阻抗随频率的变化对比Fig.3 Comparison of dimensionless horizontal dynamic resistance with frequency
4.3 算例3
为验证本文斜坡基桩水平振动响应解析解的正确性与适用性,令ω→0,即退化为水平静载下斜坡基桩解答,与Peng 等[11]基于张-花高速公路现场试验的ABAQUS 有限元软件解进行对比.基本参数如下:L=L2=18,r0=1 m,ρp=2 400 kg/m3,Ep=29 600 MPa,νs=0.3,Es=100 MPa,ρs=2 000 kg/m3,ζ=0.5.桩顶受水平荷载Q0=200 kN作用,且桩顶自由,桩端固定.通过有限元解最大位移值反算土层深度H0=1Dp,计算结果如图4 所示.图4 中纵轴坐标参照文献[11]坐标系,以桩顶为零点.
图4 表明本文解与文献[11]解吻合很好,且相比于规范法误差更小,验证了本文解的适用性.

图4 桩身水平位移结果对比Fig.4 Comparison of pile lateral displacement results
5 结论
本文基于土体三维波动方程,引入折减因子并忽略桩前一定深度范围内的浅层土体的水平抗力作用,求得斜坡桩周土水平动反力;在此基础上,利用Euler 模型推导斜坡基桩自由段以及入土段水平振动控制方程,运用传递矩阵法结合边界条件得到斜坡段基桩水平振动响应解析解,并通过退化分别与已有平地基桩水平振动响应解析解以及斜坡基桩静力变形有限元解进行对比验证了本文斜坡基桩模型解的正确性与合理性,可为斜坡基桩水平振动研究提供初步理论参考.
