B2O3/蓝宝石熔体浮力-热毛细对流的线性稳定性分析
2022-08-19莫东鸣
莫东鸣
(重庆工业职业技术学院 机械工程学院,重庆 401120)
0 引 言
提拉法是晶体生长中最常用的一种方法之一,在提拉法生长法的熔体上方添加与熔体不相溶混的液封液体,不仅可防止熔体的蒸发,也能够抑制自由界面的热毛细对流,提高晶体生长质量,该方法称为液封提拉法,在晶体生长领域中得到了广泛的推广[1]。对于液封生长技术中的双层液体系统而言,在液封液体与熔体之间的液-液界面也存在着热毛细力,加之自由界面的热毛细力、双液层中受重力影响的浮力作用的耦合,使得双层流体系统内的热对流过程变得非常复杂。近年来,越来越多的学者对双液层流体的热毛细对流不稳定性进行了研究。Li等对有上自由表面的B2O3/GaAs、5cSt硅油/H2O环形双液层进行了二维数值模拟[2-3]与渐进解的求解[4-5],结果表明,双层流体比同等条件单液层的临界Marangoni数大约两个数量级,即液封层可以大大增强流动的稳定性。莫东鸣等[1]对微重力条件下、上部为自由表面的环形双液池内的B2O3/蓝宝石熔体的热毛细对流进行了二维数值模拟,发现当Marangoni数超过临界值时,出现的失稳流型为热壁向冷壁处流动的热毛细对流失稳与近冷壁处出现的Marangoni对流。Simanovski等[6-8]对上部为固壁、垂直温度梯度与水平周期加热的边界条件,并且界面处施加热源的矩形双层系统展开了二维数值模拟,结果发现界面处的热源超过临界值会引起流动分岔的发生。
Mo等采用线性稳定性分析[9-11]对上自由表面、上固壁条件下的环形双液层的5cSt硅油/HT-70的流动稳定性进行了研究,发现了在不同的半径比、深宽比、下液层与总液层厚度比条件下,系统出现了三种流动失稳现象,即轮辐状的热流体波、轮辐状和热壁处同波数流胞叠加的热流体波,以及三维稳态流动。
综上,以上的研究多采用数值模拟,它们可以获得特定工况下的流动特征,但要系统研究特定模型下的流动稳定性临界条件,则采用线性稳定性分析。而且,针对蓝宝石晶体的液封提拉法的环形双层热毛细对流的线性稳定性研究还尤为缺乏。为此,本文对常重力条件下、上自由表面的环形液池中B2O3/蓝宝石熔体的热毛细对流进行线性稳定性分析,不仅可以丰富双液层流动系统非平衡热力学理论,更可获得液封提拉法生长蓝宝石晶体的工程指导建议。
1 物理模型及求解方法
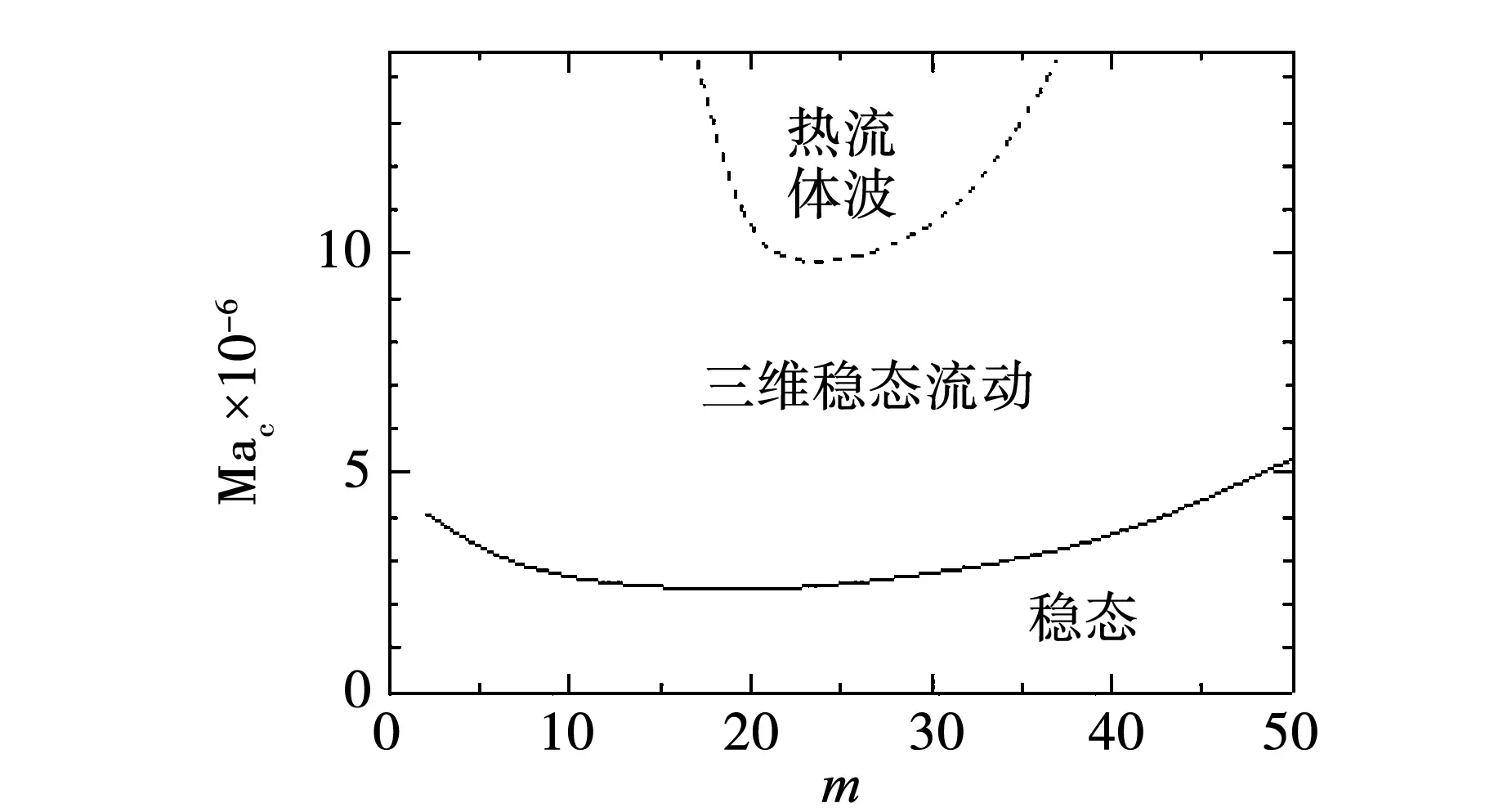
双层液体施以水平温度梯度,内壁为低温Tc,外壁为高温Th(Tc 图1 物理模型 在模型中引入如下假设:(1)熔体和液封均为不可压缩的牛顿流体,满足Boussinesq近似;(2)流速较低,流动为轴对称二维层流;(3)两相界面平整无变形,在液液界面考虑热毛细力的作用,固-液界面满足无滑移条件;(4)液池顶部和底部边界均绝热;(5)表面张力是温度的线性函数。 对控制方程进行无量纲化,时间、长度、速度、压力无量纲尺寸如下:(ro-ri)2/v1,ro-ri,v1/(ro-ri)和ρ1v12/(ro-ri)2,则无量纲方程可写为: ∇·Vi=0 (1) (2) (3) 在Z=H1=h1/(ro-ri)的液-液界面边界条件为: (4) 其中,R与Z为无量纲坐标;Ma是Marangoni数,其定义式为Ma=g2-1(Th-Tc)(ro-ri)/(m1a1);m为动力粘度;k为导热率;g2-1=-∂g/∂T是流体的界面张力梯度。 径向与纵向速度用无量纲流函数y定义如下: (5) (6) 把方程(6)代入方程(1-4)并消去非线性项,则获得线性扰动方程。于是,方程可化简为一个广义特征值问题: Ax=λBx,x∈Cn (7) 其中,A、B是具有复元素的复矩阵;n为节点数;x为特征向量,包含所取节点上的未知速度、温度和压力值的特征向量。方程(7)的特征值用IRAM(隐式重启动Arnoldi迭代法)求解。当特征值l为零时,可得到临界Marangoni数Mac。 重力条件下,B2O3/蓝宝石熔体的流动稳定性与微重力条件下发生了较大的变化,在半径比为G=0.2、径深比为η=0.1、下液层厚度与总液层厚度比ε=0.5的几何条件下,流动失稳发生了不同的分岔现象。为了详细探讨失稳特性及失稳机理,首先采用线性稳定性分析获得了边际稳定性曲线,如图2所示。通过边际稳定性曲线可以看出,在Ma-m平面上有两条边际稳定性曲线,对应有两条边际稳定性曲线的极小值,这说明在这样的几何条件下,双液层系统出现了流动分岔现象,第一个较小的临界Marangoni数Mac1=2.35×106,临界波数mc1=20,第二个较大的临界Marangoni数Mac2=9.84×106,临界波数mc2=23。代入临界Marangoni数与临界波数,求解目标特征根,可以获得流动形态特征,当2.35×106 图2 上部为固壁时微重力条件下的B2O3/蓝宝石熔体边际稳定性曲线G=0.2,ε=0.5,η=0.1 图3 常重力条件下三维稳态流动液-液界面温度波动图η=1.0,ε=0.5 图4 上部为固壁时微重力条件下B2O3/蓝宝石熔体的液-液界面温度波动G=0.2,ε=0.5,η=0.1,Ma=9.84×106,φ=31.52°,w=1.198 为了进一步揭示此种失稳机制的产生机理,通过二维数值模拟得到了Marangoni数为1.6×107时的液-液界面径向速度与温度分布,如图5(a-b),以及监测点R=0.5处的经向速度与温度分布,见图5(c-d)。当Ma=1.6×107时,此时Marangoni数大于临界Marangoni数Mac2=9.84×106,流动为靠热壁处的热流体波。从图5(a)液-液界面的径向速度看,靠近冷壁处,先是出现了一次速度的急速下降,然后再回升后继续再下降,此种特性在第一次失稳现象中未曾发现,只在二次失稳后出现。并且,速度再次升高后,并不是快速地升高到近于0的小值,而是保持了较高的速度逐渐减小。可见,正是径向的温度梯度促使热毛细力的产生,并且在近冷壁处的温度梯度越大,流动速度的变化也越大,系统的不稳定性在这个区域也越强。随着Marangoni数增大到Ma=8.0×106,超过临界值Mac2=4.528×106,此时产生了轮辐状的热流体波。并且,值得注意的是,在B2O3/蓝宝石熔体系统的下液层,温度分布呈线性分布,且靠近液-液界面比靠近底壁的温度要高。从监测点的垂向速度与温度分布来看,其分布特征与微重力条件下的该监测点的情况相似。故此,在微重力情况与常重力情况下,都出现了热壁边缘处的热流体波。 图5 G=0.2,ε=0.5和η=0.1时(a-b)液-液界面径向速度与温度(c-d)R=0.5的径向速度与温度 B2O3/蓝宝石熔体系统中,常重力下出现流动分岔现象,界面温度波动型态有两种:第一种是三维稳态流动;第二种是热流体波。与5cSt硅油/HT-70系统进行对比,可以发现,在相同几何条件下,出现了流动分岔现象,但从流动失稳临界值的对比来看,5cSt硅油/HT-70系统的临界失稳Marangoni数为1.408×106,B2O3/蓝宝石熔体系统的失稳临界值为Ma=2.35×106,与微重力情况不同,B2O3/蓝宝石熔体系统反而比5cSt硅油/HT-70系统更不容易失稳了,这说明在B2O3/蓝宝石熔体系统中,液-液界面处的热毛细对流,比浮力对流的作用更重要。 本文对常重力条件,水平温度梯度作用下,G=0.2,ε=0.5,η=0.1时,上部为上固壁的环形液池中B2O3/蓝宝石熔体的热毛细对流流动稳定性展开了线性稳定性分析,获得了以下结论。 (1)B2O3/蓝宝石熔体工质对存在两条边际稳定性曲线,第一种流动失稳是径向的三维稳态流动,第二种流动失稳是靠近热壁处的热流体波; (2)B2O3/蓝宝石熔体工质对、5cSt硅油/HT-70系统都是在常重力条件下比在微重力条件下更易失稳,说明浮力破坏了上固壁的双液层系统的流动稳定性,使流动变得更不稳定了。 (3)从流动失稳临界值的对比来看,5cSt硅油/HT-70系统的临界失稳Marangoni数为1.408×106,B2O3/蓝宝石熔体系统的失稳临界值为Ma=2.35×106,与微重力情况不同,B2O3/蓝宝石熔体系统反而比5cSt硅油/HT-70系统更不容易失稳了,这说明在B2O3/蓝宝石熔体系统中,液-液界面处的热毛细对流,比浮力对流的作用更重要。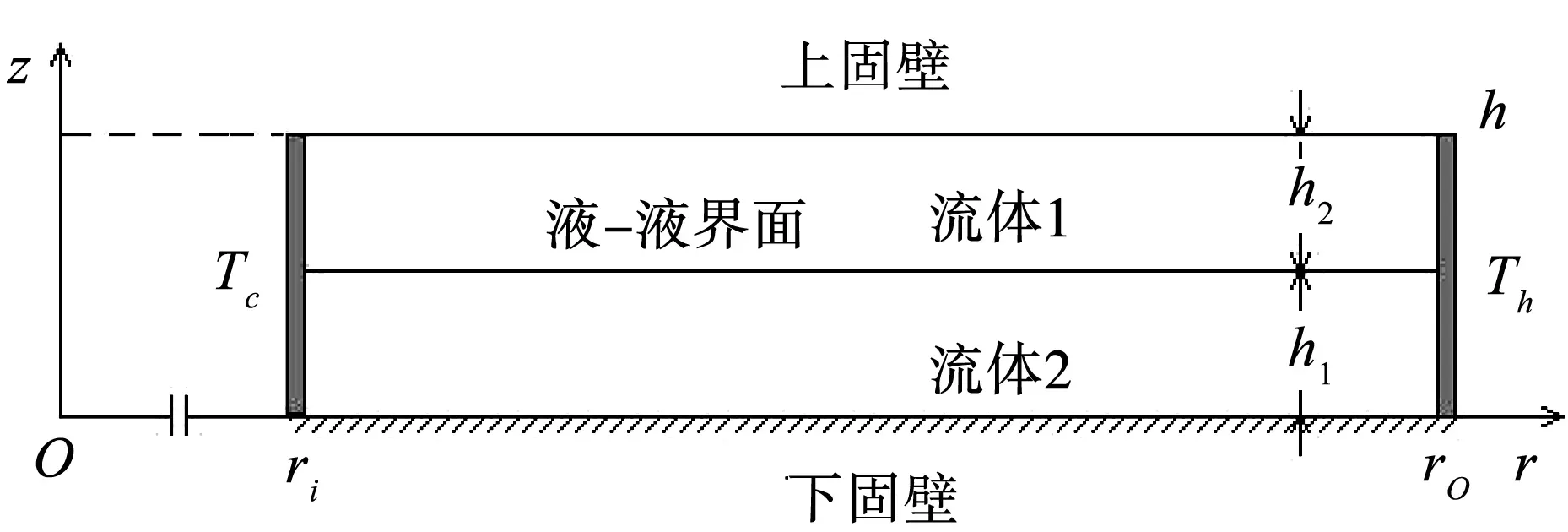


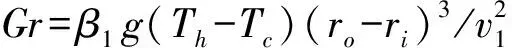
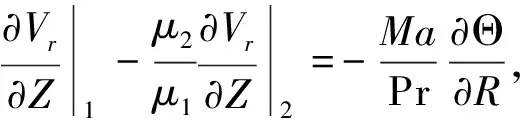
2 线性稳定性分析

3 结果与分析



4 结束语
