抓住基本图形 凸显模型意识 直击数学本质——一道中考几何压轴题的解法赏析及思考

蓝文英

(福建省厦门市海沧中学 361028)

新课标对几何教学的要求是能引导学生从复杂图形中分解出基本图形，并能分析基本图形中的基本元素及其关系，利用几何直观来进行思考,凸显模型思想，进而发展数学学科核心素养.本文通过对一道中考几何压轴题的解法探究，既呈现通性通法也展示巧思妙解，追溯几何问题本质，并引发几何解题教学的几点思考，思考解题思维与学科育人价值.

1 试题呈现

图1

(2021年福建省数学中考24题)如图1，在正方形

ABCD

中，

E

，

F

为边

AB

上的两个三等分点，点

A

关于

DE

的对称点为

A

′,

AA

′的延长线交

BC

于点

G.

(1)求证：

DE//A

′

F

;(2)求∠

GA

′

B

的大小；(3)求证：

A

′

C

=2

A

′

B.

2 优点解读

2.1 题目结构简洁美观，思维考查目标明确

本题是2021年福建省中考卷的几何压轴题，综合性强，第(2)、(3)问具有一定的难度和区分度.题干简洁优美，选用正方形为背景，结构对称，富含数学味，解法多，不仅能用常规方法解，也能用创新解法解.但要准确完成3问的解答需具备较强的思维能力，思维考查目标明确.本题考查面广，涉及的知识点多，既考查几何基本知识又考查推理运算能力，综合考查了正方形与轴对称的性质、全等三角形与相似三角形的性质、三角形中位线定理、平行线、圆、解直角三角形等基础知识.因此，本题不仅关注到中考的选拔性功能，更注重考查学生的数学能力和学科育人价值，试题立意深远.

2.2 梯度分明学思并重，立足落实核心素养

教育的根本目的是立德树人，而培育学生的核心素养是落实立德树人的有效途径.本题注重学科价值与思维并重，以发展学生的核心素养为落脚点.本题设问分明、巧设梯度、自然连贯，第(1)、(2)问为第(3)问铺设台阶，思维链长且环环相扣，难度呈螺旋式上升.第(1)问设置平行知识，旨在引导学生直观感知、捕捉基本图形的同时能够利用平行线转移角的功能，并结合全等与相似知识解决问题.第(3)问需要在前两问的基础上，借助几何直观综合分析,需具备一定的模型思想，透过现象看本质.因此，第(3)问难度大、区分度高，集中考查运算推理能力、空间观念与直观想象以及转化思想，特别是有序有向思考的能力，有效考查学生的核心素养，具有较强的学科育人功能.

3 解法探究

问题(1)比较基础，大部分学生能够利用三角形中位线知识完成解答；问题(2)、(3)思维含量高，解法丰富，不同思维层次的学生呈现出不同的解法.学生借助几何直观，抓住基本图形或者结合模型思想，能够找到问题的突破口.下面针对问题(2)、(3)，给出几种典型解法.

3.1 建构常规思维，立足自然解法

第(2)问是求∠

GA

′

B

，初中阶段可以直接从特殊角入手，通过构造直角三角形，使待求角成为直角三角形中的一个内角.结合三角函数和勾股定理，发现所构造的三角形正好是等腰直角三角形，进而得出待求角为45°.

解法1 从特殊角入手，构造直角三角形

图2

如图2，过点

B

作

BH

⊥

AG

于点

H

，则∠

AHB

=90°.在正方形

ABCD

中，

AD

=

AB

,∠

DAB

=∠

ABG

=90°.设直线

DE

与

AA

′交于点

O

，因为点

A

和

A

′关于

DE

对称，所以

DE

垂直平分

AA

′，即

DE

⊥

AA

′，

AO

=

OA

′.所以∠

AOD

=90°，即∠

ADE

+∠

DAO

=90°.又因为∠

BAH

+∠

DAO

=90°，所以∠

ADE

=∠

BAH

，△

DAE

≌△

ABG

，

AE

=

BG.

不妨设

AE

=

a

，则由

E

和

F

为

AB

边上的两个三等分点，得

AE

=

EF

=

FB

=

BG

=

a.

在Rt△

A

′

HB

中，设

BH

=

x

，因为则

AH

=3

x

，所以

AH

+

BH

=

AB

,即(3

x

)+

x

=(3

a

),解得同理，由第(1)问可知∠

AA

′

F

=90°.在Rt△

AA

′

F

中，不妨设则

A

′

A

=3

y.

所以

A

′

A

+

A

′

F

=

AF

，即(3

y

)+

y

=(2

a

)，解得所以所以Rt△

A

′

HB

是等腰直角三角形，即∠

GA

′

B

=45°.

解法2 利用相似三角形

如图2，过点

B

作

BH

⊥

AG

于点

H

，则∠

AHB

=90°.由

DE

垂直平分

AA

′，得

OA

=

OA

′，∠

AOE

=∠

AHB

=90°，所以

DE

∥

HB.

又由第(1)问知

DE

∥

A

′

F

，故

DE

∥

A

′

F

∥

HB

，不妨设

AE

=

a

，则由

E

和

F

为

AB

边上的两个三等分点，知

AE

=

EF

=

FB

=

a.

所以又因为

OA

=

OA

′，故

A

′

H

=

AO

=

A

′

O.

易证△

AOE

∽△

DAE.

所以所以Rt△

A

′

HB

是等腰直角三角形，∠

HA

′

B

=45°，∠

GA

′

B

=45°.

3.2 抓住基本图形，探寻创新解法

复杂几何图形是由多个简单的基本图形叠加或者组合而成，借助几何直观和空间想象思考图形之间的关联，从整体到局部地观察图形的结构特征，抓住基本图形，就等于握住了解题的“金钥匙”，也就打开了通往解题的康庄大道.波利亚在《怎样解题》中说过：“当我们的问题比较困难时，我们可能感到很有必要进一步把问题再分解成几部分，并研究其更细微的末节.”因此，解决几何问题的一个基本策略就是仔细推敲题目条件，寻找与其关联的基本图形，感知基本图形所获得的相关结论及其隐含的线索.从图3(1)中发现，四边形

A

′

FBG

中有一组对角为直角，很容易通过作垂线段构造矩形.同时该四边形有一组对角互补，联想到四点共圆，从而能得出创新解法3和特殊解法5.由图3(2)、3(3)的发现，较容易想到可以通过旋转△

A

′

FB

或△

A

′

BG

，进而得到创新解法4.可见，通过基本图形可以将陌生的、复杂的图形转化为熟悉的图形，从而发现解题方向，这不仅是几何教学的基本策略，也是本题特殊解法的重要源泉.

图3

解法3 旋转全等

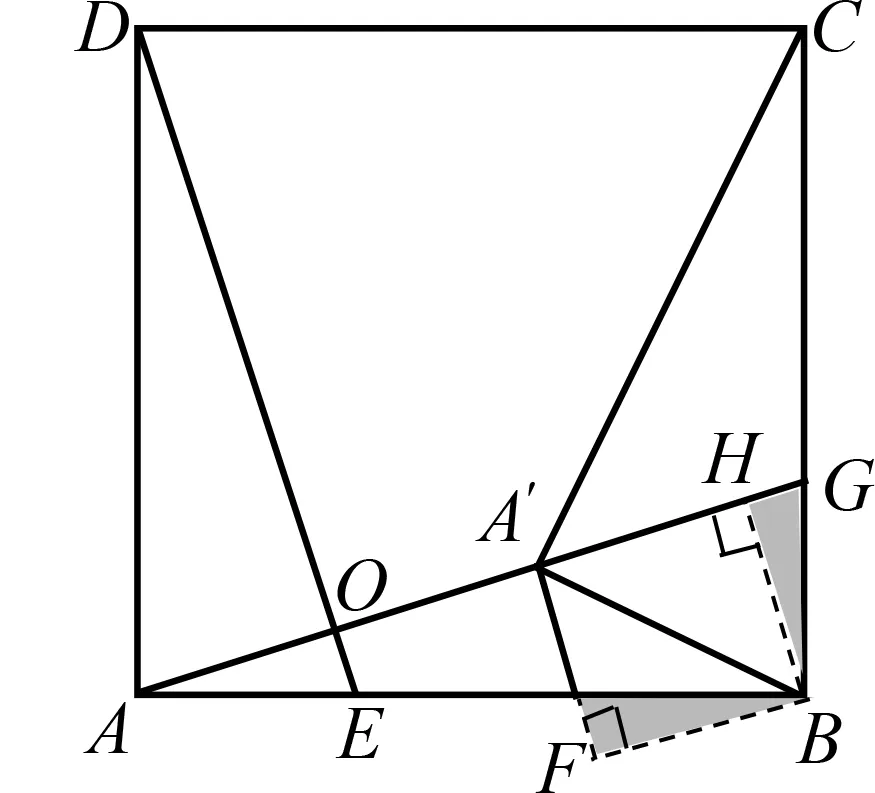
图4

如图4,分别过点

B

作

BH

⊥

AG

于点

H

，作

BP

⊥

A

′

P

于点

P

，则∠

A

′

HB

=∠

A

′

PB

=90°.由第(1)问知∠

GA

′

P

=90°，所以四边形

A

′

PBH

是矩形，∠

PBH

=90°，即∠

PBF

+∠

FBH

=90°.又因为在正方形

ABCD

中，∠

ABC

=90°，得∠

HBG

+∠

FBH

=90°，∠

HBG

=∠

PBF.

又因为∠

BHG

=∠

BPF

=90°，由解法1可知

FB

=

BG

=

a

，则△

BHG

≌△

BPF

(AAS)，所以

BH

=

BP

，所以矩形

A

′

PBH

是正方形，

A

′

H

=

HB

，Rt△

A

′

HB

是等腰直角三角形，即∠

GA

′

B

=45°.解法4 如图5，过点

B

作

BA

′的垂线交

A

′

G

的延长线于点

H

，∠

A

′

BH

=90°，得∠

A

′

BG

+∠

GBH

=90°.因为在正方形

ABCD

中，∠

ABC

=90°，所以∠

FBA

′+∠

A

′

BG

=90°，∠

FBA

′=∠

GBH.

在四边形

A

′

FBG

中，∠

ABG

=∠

FA

′

G

=90°，则∠

A

′

FB

+∠

A

′

GB

=180°.又因为∠

BGH

+∠

A

′

GB

=180°，所以∠

BGH

=∠

A

′

FB.

由 解法1可知

FB

=

BG

=

a

，所以△

A

′

FB

≌△

HGB

(ASA)，

A

′

B

=

HB

，Rt△

A

′

BH

是等腰直角三角形，即∠

GA

′

B

=45°.

图5 图6

当然，如图6，如果过点

B

作

BA

′的垂线交

A

′

F

的延长线于点

H

，∠

A

′

BH

=90°，则∠

A

′

BF

+∠

FBH

=90°.因为在正方形

ABCD

中，∠

ABC

=90°，所以∠

FBA

′+∠

A

′

BG

=90°，∠

FBH

=∠

A

′

BG.

在四边形

A

′

FBG

中，∠

FBG

=∠

FA

′

G

=90°，所以∠

A

′

FB

+∠

A

′

GB

=180°.又因为∠

A

′

FB

+∠

BFH

=180°，得∠

BFH

=∠

A

′

GB.

由解法1可知

FB

=

BG

=

a

，则△

A

′

GB

≌△

HFB

(ASA)，

A

′

B

=

HB

，Rt△

A

′

BH

是等腰直角三角形，∠

HA

′

B

=45°，∠

GA

′

B

=45°.

解法5 构造辅助圆，四点共圆

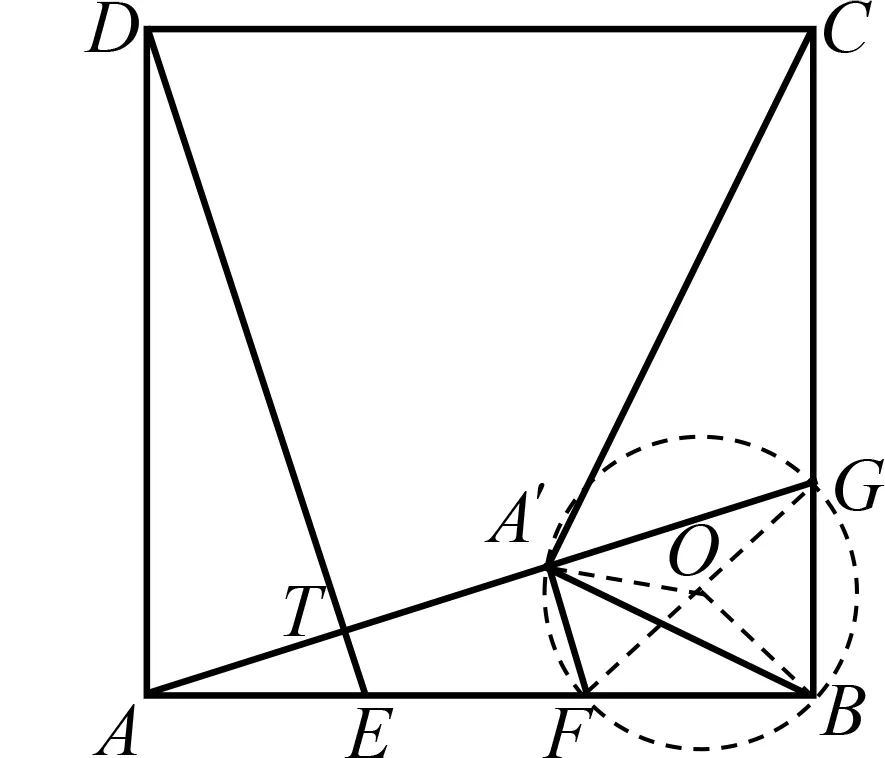
图7

如图7，取

FG

的中点

O

，连结

OA

′，

OB.

由第(1)问可知

DE

∥

A

′

F

，则

A

′

F

⊥

AA

′,所以∠

FA

′

G

=90°.在正方形

ABCD

中，∠

ABG

=90°.在Rt△

FA

′

G

和Rt△

FBG

中，所以

OF

=

OB

=

OG

=

OA

′，点

A

′，

F

，

B

，

G

四点在以

O

为圆心、

OA

′为半径的同一个圆上.根据同弧所对的圆周角相等，∠

GA

′

B

=∠

GFB

，由解法1可知△

DAE

≌△

ABG

，

AE

=

BG.

又因为

E

和

F

为

AB

边上的两个三等分点，得

AE

=

EF

=

FB

=

BG

，所以Rt△

FBG

是等腰直角三角形，∠

GFB

=45°，∠

GA

′

B

=∠

GFB

=45°.

3.3 借助几何直观，直击问题本质

余文森教授提出的“读思达”教学法同样适用于解题教学，数学解题过程其实就是一个阅读、思考、表达的过程.几何题阅读的不仅仅是题干信息，更是一个阅图、思图的过程.在阅图的过程中，几何直观发挥了不可或缺的作用.几何直观主要是指利用图形描述和分析问题,其本质是对几何图形产生的一种强烈的直觉感知.比如本题第(3)问要证

A

′

C

=2

A

′

B

，即证明两条线段的数量关系，依然要回归图形，从图形中发现蛛丝马迹，仔细观察图形，通过敏锐的直觉容易联想到相似.看到图形直观感知到的联想往往是解题的方向，顺着解题方向获得猜想，进而再结合第(2)问的结论，容易获得证法1.同样，此问证法2和3依然是依托强烈的直观想象和空间观念，利用相似这一基本知识叠加轴对称性完成解答.证法1、2、3本质是一样的，都是证明相似得到线段的比例关系.因此,借助几何直观，不仅能感知问题解决的方向和思路，更能预测可能的结果，直击几何问题的本质.第(3)问的解法展示如下：

证法1 勾股定理+三角函数+相似

图8

如图8，由第(2)问中的解法1，可得△

DAE

≌△

ABG

,则

AE

=

BG.

不妨设

AE

=

a

，则由

E

和

F

为

AB

边上的两个三等分点，得

AE

=

EF

=

FB

=

BG

=

a.

在Rt△

ABG

中，由勾股定理可得同理，由第(1)问可知∠

AA

′

F

=90°.在Rt△

AA

′

F

中，不妨设

A

′

F

=

x

，tan∠

A

′

AF

=则

A

′

A

=3

x

,

A

′

A

+

A

′

F

=

AF

，即(3

x

)+

x

=(2

a

),解得所以又因为在正方形

ABCD

中，∠

ABC

=90°，由(2)得在四边形

A

′

FBG

中，∠

FBG

=∠

FA

′

G

=90°.由四边形内角和可得∠

A

′

FB

+∠

A

′

GB

=180°，又∠

A

′

GC

+∠

A

′

GB

=180°，所以∠

A

′

FB

即

A

′

C

=2

A

′

B.

证法2 如图9，连结

A

′

D

，在正方形

ABCD

中，

AD

=

DC

,∠

ADC

=90°.因为

DE

垂直平分

AA

′，所以

AD

=

A

′

D

=

DC

，从而∠1=∠2，∠3=∠4.在四边形

ADCA

′中，由∠1+∠2+∠3+∠4=270°，得2(∠2+∠3)=270°，∠

AA

′

C

=135°，∠

CA

′

G

=45°.由第(2)问得∠

GA

′

B

=45°，∠

FA

′

G

=90°，所以∠

FA

′

B

=45°，∠

CA

′

G

=∠

FA

′

B

=45°，又因为∠

A

′

FB

+∠

A

′

GB

=180°，∠

A

′

GC

+∠

A

′

GB

=180°，所以即

A

′

C

=2

A

′

B.

图9 图10

证法3 如图10，连结

A

′

D

，过点

B

作

BM

∥

A

′

C

交

A

′

G

的延长线于点

M

，由本问的证法1可得∠

CA

′

G

=45°，由第(2)问得∠

GA

′

B

=45°，所以∠

CA

′

B

=90°，∠

A

′

BM

=180°-∠

CA

′

B

=90°，△

A

′

BM

是等腰直角三角形，

A

′

B

=

BM.

又因为

BM

∥

A

′

C

，所以从而即

A

′

C

=2

A

′

B.

3.4 紧扣基本模型，挖掘特殊解法

“数学家波利亚在《怎样解题》中说：‘解题的成功，要靠正确的转化’”.如果能将一些常见的、重要的基本模型进行提炼并深入研究，在解题中往往能起到化难为易的效果.比如常见的手拉手模型、角平分线模型、平行下的相似、一线三垂直模型等.模型思想是直观想象素养的重要组成部分，解题过程中有意识地去分解或者构建模型，不仅能拓展思维、开拓思路，更能培养创新性思维和多角度思考问题的能力，进而挖掘出多种灵巧的解法.有时题中呈现的基本模型与条件并不吻合，这时需关联相关知识，通过添加辅助线构建与之匹配的基本模型，以达到顺利解题的目的.本题第(3)问中的特殊解法的探究思路是聚焦基本模型，如图11，证法4中的角平分线基本模型是解决本问的一个题眼，在得到

A

′

G

是角平分线的时候，很自然地想到其性质，通过构造两条垂线段，利用面积法顺利解决问题.如图12，证法5则综合运用等腰三角形以及正方形背景下的一线三垂直模型，成功突破思维瓶颈.纵观本问的多种解法，无论是常规解法还是创新解法，基本图形与基本模型从始至终都贯彻于整个解题思维过程中.

图11 图12

证法4 如图11，过点

G

作

GM

⊥

A

′

C

于点

M

，作

GN

⊥

A

′

B.

由本问证法3可知∠

CA

′

B

=90°，四边形

A

′

NGM

是矩形.由第(2)问得∠

GA

′

B

=45°，则∠

CA

′

G

=45°，△

GA

′

N

是等腰直角三角形，所以

A

′

N

=

NG

，矩形

A

′

NGM

是正方形，于是即

A

′

C

=2

A

′

B.

证法5 如图12，连结

A

′

D

，过点

D

作

DM

⊥

A

′

C

于点

M

，则∠

DMC

=90°.在正方形

ABCD

中，

AD

=

DC

=

CB

,∠

DCB

=90°.因为

DE

垂直平分

AA

′，得

AD

=

A

′

D

=

DC.

又因为

DM

⊥

A

′

C

，得

A

′

C

=2

CM

(三线合一).因为∠

DCA

′+∠

A

′

CB

=90°，在Rt△

DMC

中∠

DCA

′+∠

CDM

=90°，所以∠

A

′

CB

=∠

CDM

， △

DMC

≌△

CA

′

B

，

A

′

B

=

MC

，

A

′

C

=2

CM

=2

A

′

B

，

A

′

C

=2

A

′

B.

4 教学思考

4.1 凸显模型意识，促成解法多元

本题第(2)、(3)问从学生最为熟悉的正方形十字架模型切入，不论是构造垂线还是从熟悉的平行线证相似,从始至终贯穿了数学模型思想.从基础的十字架、平行线模型到叠加型模型，如一线三垂直模型、四点共圆等模型.第(2)问的难度逐渐增大，若没能做好铺垫，就很难突破第(3)问，借助模型思想可有效缩短思维链，提高解题效率，快速生成通性通法及一系列的巧解.求∠

GA

′

B

，通过构造直角三角形把求角问题转化为求边的比例关系，再结合正方形十字架模型巧妙构造旋转变换，充分连通条件与结论的通道，使思路成型.在实际教学中教师应善于渗透模型思想，紧扣基本图形和基本模型，以教材中的基本知识和中考题中的常见基本图形为蓝本，以基本模型为桥梁，感悟模型的本质，并将解法和题型及其对应的模型归类，通过对基础模型追根溯源、融会贯通构造复合模型，不断地培养学生的数学创造性思维，进而提高解决问题的能力.

4.2 扎根直观想象，提升数学思维

《义务教育数学课程标准(2011年版)》提出的十个核心关键词中包含了空间观念、几何直观、模型思想和应用意识，这是数学学科核心素养的关键组成部分.而直观想象则是中学数学六大核心素养之一.本题第(3)问的常规解法与多种巧解均是建立在强烈的直观想象的基础上，要证明

A

′

C

=2

A

′

B

，需要仔细观察图形特征，猜想△

A

′

FB

∽△

A

′

GC.

同时，在第(2)问的基础上发现

A

′

G

平分∠

GA

′

B

，能快速联想到角平分线基本模型，构造垂线段完成证法4.直观想象好比灯塔，为解题指明了方向，扎根直观想象能感知图形的形态与变化，通过已有数学经验、直觉思维和数形结合思想，建构几何问题的直观模型,合情合理探寻解题思路，预测结果.因此，在双减背景下，教师在日常的几何解题教学中应注重培养学生的直观想象能力，引导学生抓住图形的特点，紧扣基本模型分析问题、推敲题意、感悟模型中所蕴藏的思想方法，借助几何直观与空间观念，大胆构建与题干关联的基本模型，锁定解题策略，提高解题能力，更好地培养学生思维的灵活性，真正做到减负不减质.