有机融合线上线下教学优势着力提升常态课堂教学质量*
2022-08-19童先峰
童先峰
(江苏省张家港市教师发展中心 215600)
壬寅年初,突如其来的疫情打乱区域开学节奏,学生不能如期返校上课后,各校第一时间制定了“一校一策”线上教学方案,瞬间就将线上教学从原先的外挂或应急角色转变为与线下教学并行的教学方式.
但在多数师生家长的潜意识中,线上教学的效果与线下教学相比肯定是打一定折扣的.也确实如此,从对线上教学的问卷调查来看,学生们反馈线上学习存在的主要问题是听讲时容易走神分心,师生、生生交流受限(图1).与此同时,学生们一致认为,通过回看视频实现“哪里不会点(倍速、拖动、暂停)哪里”的学习方式是线上教学最大优势所在(图2).

图1 线上学习缺陷 图2 线上学习优势
反观线下教学优势,主要体现在:对学生而言,有与同伴合作互学的真实情境,能面对面进行语言、表情、动作等多形式的情感交流;对教师来说,有直接抓手组织教学,能最大限度收集学情、利用学情、让学情主导课堂教学.
而从近期教学调研了解的情况来看,回归学校后的常态课堂教学并没有很好地发挥线下优势,却在很大程度上呈现出线上教学的不足:教师“一言堂”“满堂灌”“扶贫式”逐题讲评、就题论题讲解、师生问答“一对一”、其他学生“正襟危坐”……文科教学逐渐“窄化”为反复背诵默写(死记硬背),理科教学慢慢“沦陷”为大量重复刷题(题海战术),一定程度上导致学有余力的学生未能形成突破学习瓶颈的真知识、真技能、真能力;学习能力中等的学生仅仅知道答案“是什么”而不明白“为什么”;学有困难的学生“习得性无助”,大多时间处于“人在心不在”的课堂状态.
分析出现上述现象的原因,依旧与多数教师没有正确认识“教学是一个完整的过程”有关,也与一贯以来“非此即彼”“非黑即白”的思维惯势有关.要么认为教学就应该以“教”为主,但在实践中又缺少高屋建瓴的办法和有效的教学策略,教师不能高水平教直接影响学生高水平学;要么意识到了“以学为核心”却走向了“去教师化”的极端,但事实是在课堂教学的范畴中,如果没有教师真正的教就根本不可能有学生真正的学.因此,本文就在常态课堂教学中如何将线上线下教学优势进行有机融合,聚焦“双减”增效减负,提供几个教学策略,仅供一线教师参考.
1 充分发挥线下小组合作学习优势,通过精心设计“问题链”,搭建学习支架,让“思维可视化”
聚焦知识整合关联,重视思维建构过程,通过大问题小台阶设计,在障碍处提供支持,引领学生从旧知走向新知、从新知走向未知,夯实“双基”.
课前,教师根据习题批改后的错误统计及对学情的预估,精心设计小组合作学习讨论的“问题链”,并通过投影展示.课上,教师明确任务,组织开展协同学习,指导学生在同伴互动中顺着问题支架拾阶而上.课中,教师就共性问题简明扼要点拨释疑,实现精准“靶向治疗”;同时,对更高水平的见解,分享其优秀解法,注重课堂实时生成.
案例1
基础题教学(片段)如图3和图4所示.

图3 试卷习题(部分)

图4 “问题链”支架(部分)
简评
一般而言,尽管学生基础题部分出错的概率相对较低,但也会出现一些问题.教师常纠结于“不讲不放心、讲了又味同嚼蜡”的困境,但受以学科均分为考核“指挥棒”的影响,于是乎,眉毛胡子一把抓式“面面俱到”,以致学生听得烦、听得累、听得索然无味.方式一变天地宽,有了学习支架的支持,可有效避免课堂上小组讨论的随意性,可充分发挥学生朋辈互助的效能,学生(特别是学有困难的学生)在师生、生生互动评价中全身心投入学习活动,进而激活已有经验、建立知识关联、获得成功体验.
2 充分发挥线上线下协同研修优势,通过精心绘制“施工图”,提炼思维模型,让“知识结构化”
聚焦知识重难点瓶颈,强化教学内容结构化组织,总结提炼学科思想方法,凸显学科核心概念、关键能力,引领学生一起深入研讨,提升“四能”.
日常研修中,教师在整合教材、试卷、习题册等相关内容基础上,精心设计典型例习题的教学“施工图”,做到条理清晰且注意梯度层次,并通过知识点激活、联想、串讲,注重一题多解、多题一解,将高价值、重难点问题讲深、讲透、讲到位,帮助学生理清知识脉络,提升能力素养.
案例2
能力题讲评片段1 如图5,在Rt△ABC
中,∠ACB
=90°,CB
=4,CA
=6,⊙C
的半径为2,P
为圆上一动点,连结AP
,BP
,求的最小值.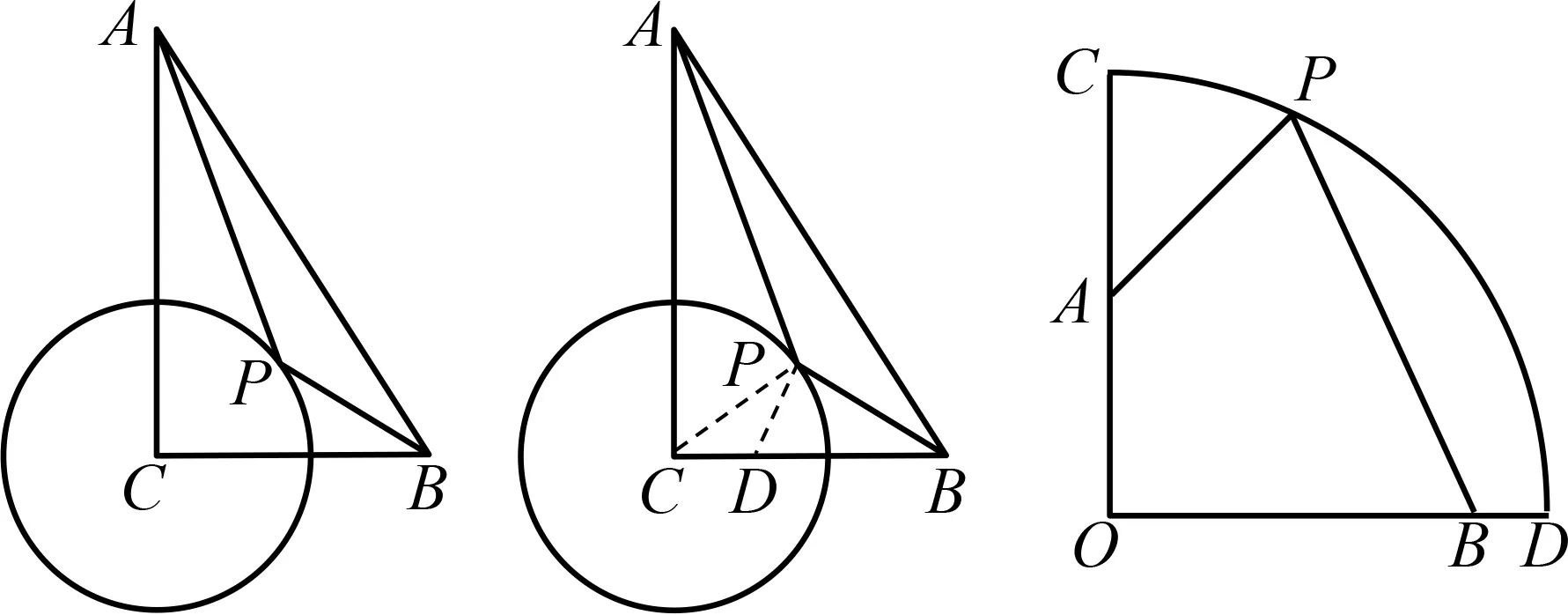
图5 图6 图7
(1)尝试解决:如图6,连结CP
,在CB
上取点D
,使CD
=1,则有又因为∠PCD
=∠BCP
,所以所以故请你完成余下的思考,并直接写出答案:的最小值为.(2)自主探索:在题目条件不变的情况下,的最小值为
.(3)拓展延伸:如图7,已知扇形
COD
中,∠COD
=90°,OC
=6,OA
=3,OB
=5,点P
是弧上一点,求2AP
+PB
的最小值.教学“施工图”如图8和图9所示.
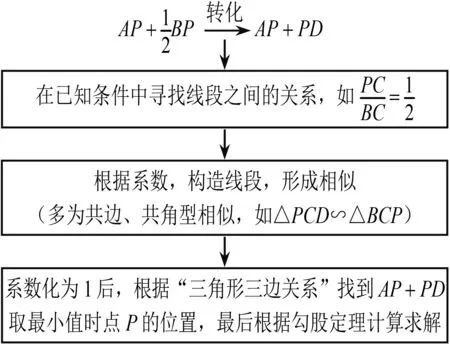
图8 第(1)题
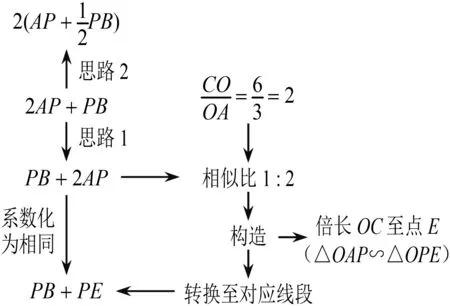
图9 第(3)题
片段2 如图10,已知△ABC
是边长为1的等边三角形,点D
在线段BC
上,DE
⊥AB
,DF
∥AB
,则;的最小值为
.
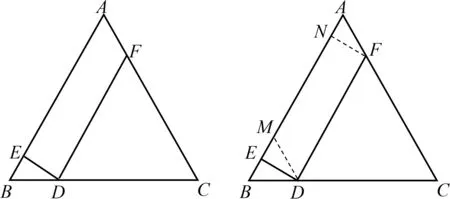
图10 图11
教学“施工图”如图12和图13所示.
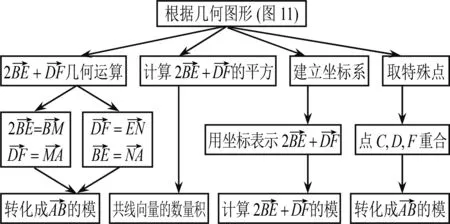
图12 第(1)题
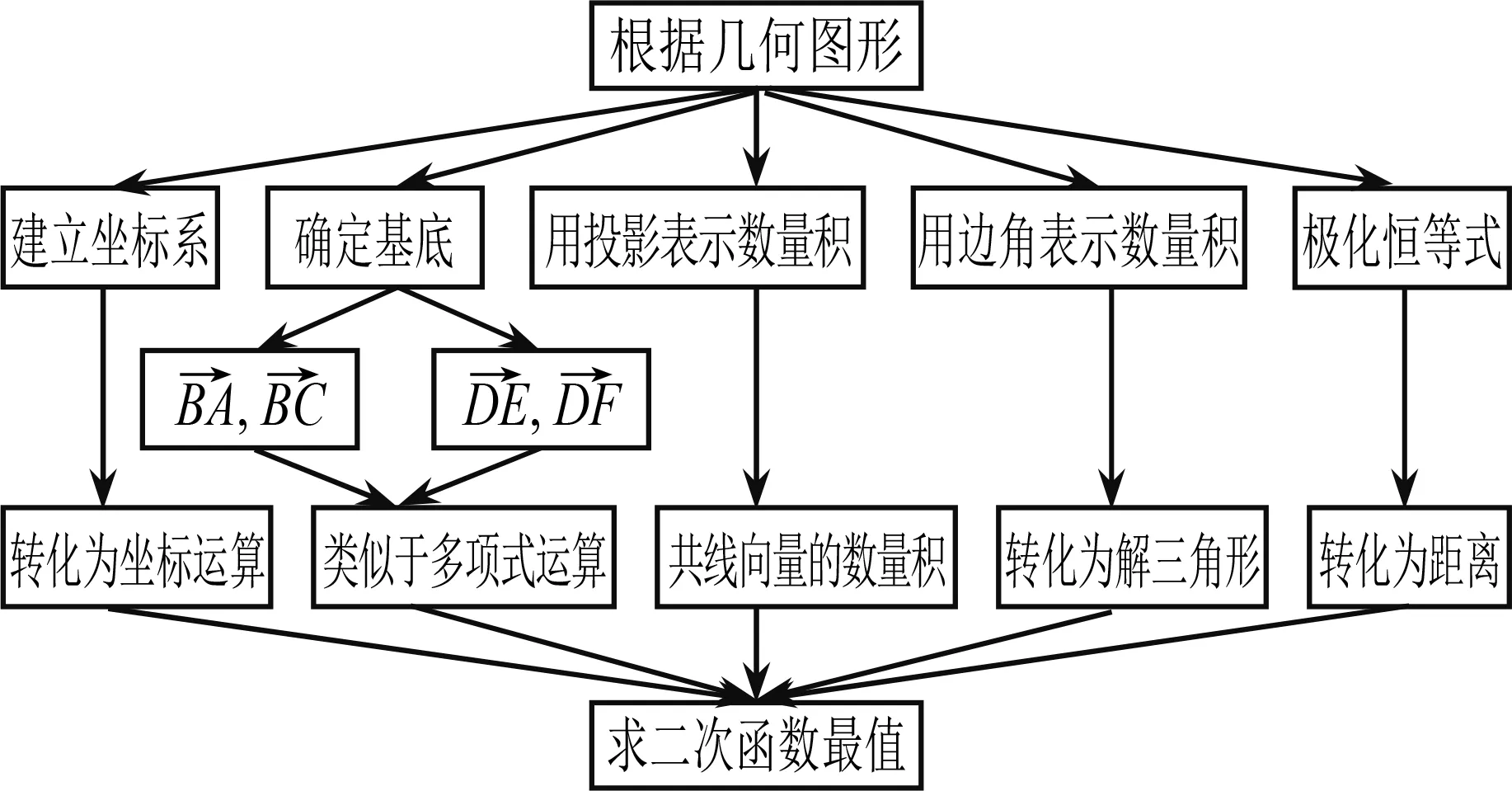
图13 第(2)题
简评
上述两个案例,均围绕主干问题由浅入深进行梳理总结,通过教师提纲挈领讲解、讲演、讲评“放大招”,对不同解题策略进行指点迷津,亦或是另辟蹊径“秒杀技巧”,帮助学生扫除知识盲区、提炼解题方法、形成能力体系架构.从这个意义上来讲,“施工图”就是课堂教学的线路图,可有效避免教学过程中“脚踩西瓜皮、滑到哪里是哪里”,减少无效或低效教学行为的发生.3 发挥线上教学过程可回溯优势,通过精心制作“微视频”,促进思维建构,让“学习个性化”

图14 微视频二维码
满足学生个性化学习的回看需求,依托信息技术,教师精心制作“微视频”(一般每个12分钟左右),提供对教学关键环节可回溯、可翻转的学习途径.如整合课堂教学中学生的独特见解,做好当天重点、难点突破的过程录制;如做好举一反三,录制“三天两压轴题”“每日一中档题”微视频(图14),指导学生借助所学知识、技能来解决更高水平的疑难问题,培养迁移和应用能力.
案例3
已知二次函数y
=ax
+bx
+c
(a
≠0)的图象过点(-1,0),且对任意实数x
,都有4x
-12≤ax
+bx
+c
≤2x
-8x
+6.(1)求该二次函数的解析式;
(2)若(1)中二次函数图象与x
轴正半轴的交点为A
,与y
轴的交点为C
,点M
是(1)中二次函数图象上的动点,问在x
轴上是否存在点N
,使得以A
,C
,M
,N
为顶点的四边形是平行四边形?若存在,求出所有满足条件的点N
的坐标;若不存在,请说明理由.简评
就目前来说,学生学习仍以课堂学习+课后作业为主要方式,做好知识点的循序渐进和深化巩固.白天课堂教学中,一是对于某些难题“囫囵吞枣”听一遍后真不一定能明白,二是局限于一节课时间,难题也研究不了几个(包括不同解法);而在晚上写作业的过程中,如果遇到不会、不懂的问题又不能在第一时间得到帮助解决,导致部分学生的学习障碍像滚雪球一样,不经意间就“深陷泥潭”.因此,需要每天有“鲜活”的问题驱动,学生借助视频讲解,能有自主时间来研究疑难问题的解题方法,开阔解题思路、提升解题能力.此外,以微视频驱动规模化教育与个性化培养方式也有利于校本资源库建设的提档升级,经过备课组一届又一届选编、改编、创编后的优质视频资源可更好地服务于师生发展.后续还可进一步利用信息技术做好日常作业分析诊断,通过精心设计作业的“微清单”来减量提质,进而撬动课堂教学深层次改革创新,实现从“生”“动”到“生动”的蜕变.
