基于改进Dijkstra算法的防冲突最短路径规划研究
2022-08-18黄翼虎于亚楠
黄翼虎,于亚楠
(青岛科技大学自动化与电子工程学院,山东 青岛 266061)
0 引 言
在现代化战争时代,作战环境以及作业任务的多样化已经使得单架无人机不能独自应对严格多变的作战需求,因此,实现多无人机合作完成作业任务已然逐渐成为了专家学者们的关注热点[1-2]。无人机群要想实现协同合作来完成作业任务首先面临的就是路径规划问题,只有为无人机规划出最短且互不冲突的航线才能保证作业任务的顺利完成。国内外的研究人员针对此问题归纳总结了遗传算法[3-4]、Dijkstra算法[5-7]、A*算法[8-9]、人工势场算法[10-11]等多种算法。上述算法里,Dijkstra算法是在有权图里搜寻最短路线已经发展较为成熟的经典算法,其采取的是贪婪搜索策略,由起始点开始逐步地向其他节点搜索,直至目标点停止,利用回溯数组进行节点回溯就必定能够找出一条最短可行路线,由此在路径规划问题中被普遍使用[12-13]。
传统Dijkstra算法在规划多作业任务时,通过回溯数组仅仅可以给出各任务的一条最短可行路线,却不能给出各任务包含总长度相等的全部最短可行路线,而且没有把各任务在执行过程中可能存在的路线冲突问题考虑在内[14-15]。为解决多无人机在执行作业任务时可能发生的冲突问题,本文在经典Dijkstra算法执行的过程中,通过引入变长回溯数组来改进其搜索方式,使其能够回溯出各任务包含总长度相等的全部最短可行路线,再通过引入时间窗冲突判断模型来解决路线冲突问题。应用Matlab来设计并编写程序进行算法验证,结果表明在规划多作业任务时,引入变长回溯数组的改进Dijkstra算法能够找出各任务存在的全部最短可行路线,时间窗冲突判断模型可以有效地避免多任务执行时的路线冲突问题并规划出互不冲突的最短路线。
1 改进Dijkstra算法
1.1 相关概念
进行作业任务时的带权路线图表示为:
G=(N,E,W)
(1)
其中,N为带权路线图中n0,n1,…,nn全部可行航迹节点的集合;E为路线图中e0,e1,…,en所有边的集合;W为路线图中w01,w02,…,wnn所有边的权值集合,本文中特指为相邻两节点间的直线长度。
有权路线图的数学表达式以邻接矩阵A表示为:
(2)
其中,aij为节点ni和nj间的长度。若两节点相邻,其值为wij;若两节点不相邻,其值为∞;若i=j,其值为0。
1.2 改进Dijkstra算法步骤
经典Dijkstra算法以广度优先思想从起始点开始逐步向外扩展直至搜索到全部节点结束,在遍历节点的过程中,通过记录距离该节点最近的前驱节点而后生成回溯向量[16-17],凭借回溯向量找出一条由起始点至目标点最短距离的可行路线。但是经典Dijkstra算法运行产生的回溯向量仅记录各节点的一个前驱节点[18],因此引入变长回溯数组来记录各节点存在的全部前驱节点,以此得到各作业任务包含总长度相等的全部最短可行路线。为便于表述,定义下列变量符号:
1)A为作业任务的带权路线图的邻接矩阵。
2)st为任务的起始节点。
3)e为任务的目标节点。
4)S为已经明确路线的节点所组成的向量。
5)D为最短长度向量。D[i]代表由起始节点st遍历至节点ni的最短总长度。
6)P为作业任务路线中各节点的变长回溯数组,P[i]表示为节点ni的所有前驱节点。
引入变长回溯数组改进Dijkstra算法搜索最短可行路线的步骤如下:
step1S和D初始化。此时S中只包含起始节点st,即S={st},D[i]=ast,i,i=1,2,…,n。
step2从起始节点向外遍历其他节点,找到节点nj,使得D[j]=minD,令S=S∪{nj}。
step3以节点nj为中心点向外遍历,更改D中的最小值以及各节点的变长回溯数组。
即若:
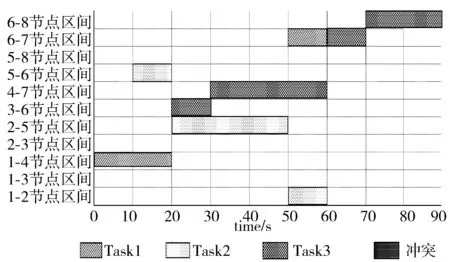
D[j]+ajk (3) 则将D更改为: D[k]=D[j]+ajk (4) 将P[k]存放的前驱节点全部清除,记节点k的前驱节点为j,将j存放到P[k]。 若: D[j]+ajk=D[k] (5) 则在原来P[k]存放前驱节点的基础上,再将j存放到P[k]。 step4循环step2~step3,直到所有节点都被搜索。 引入变长回溯数组后,通过查询回溯数组可得到所要执行任务的总长度相等的全部最短可行路线,但是这不能保证各任务路线在执行过程时不发生冲突矛盾。因此,为了得到各任务之间互不冲突的路线,引入了时间窗冲突检测模型。 时间窗是一种用来表示在有权路线图中执行作业任务的何时处于何地的方法[19-20]。因为具备实现简单和实用性强等特点,时间窗在路径规划问题中被普遍使用[21]。 本文建立时间窗模型的假设条件包括: 1)将无人机在移动过程中视作质点,忽略其形状和大小且都在同一高度上飞行。 2)带权路线图中节点之间为单行道,即同一时间段内每条边只允许一架无人机飞行,但可双向通行,不计节点处的长度。 3)无人机以V0=1 m/s匀速移动,忽略其加减速及转弯时所用的时间。 4)Administrator可以设定作业任务的优先等级,一般默认为产生作业任务的时间序列[22]。 本文中时间窗具体指无人机在所规划的航线上飞行时,到达航迹节点的具体时间点以及在节点之间所占用的时间区间。时间窗模型[23-24]如下: TWn=[ti,ti+1],i=1,2,…,end (6) (7) 其中,TWn为第n架无人机执行任务时的航线时间窗;ti和ti+1为该无人机到达航线中第i个和第i+1个航迹节点的时间点;D(i,i+1)为该无人机任务航线中第i个和第i+1个航迹节点间的长度。根据以上公式,可以得到该无人机从起始点至目标点所产生的时间窗。 多无人机发生航线冲突的本质是多个任务在执行过程中同时占用了同一节点或节点区间,时间窗能详细反映无人机何时在何地的状态信息[25-26],为之后判别及解决航线冲突问题提供了前提条件。 为便于表述,引入以下字母符号: 1)to(i)为已完成的任务中i节点的占用时刻。 2)tn(i)为当前的任务在i节点的占用时刻。 3)starto(i,j)为已完成的任务中i-j节点区间的开始占用时刻。 4)startn(i,j)为当前的任务在i-j节点区间的开始占用时刻。 5)endo(i,j)为已完成的任务中i-j节点区间的结束占用时刻。 6)endn(i,j)为当前的任务在i-j节点区间的结束占用时刻。 改进Dijkstra算法引入时间窗冲突判断模型的步骤如下: step1根据作业任务的带权路线图生成邻接矩阵,设定任务优先等级并生成任务作业列表[27]。 step2运用改进Dijkstra算法对当前任务作业列表中还没有执行的优先等级最高的任务进行规划,生成该任务包含总长度相等的全部最短可行路线的时间窗。 step3依次判断当前任务的所有最短可行路线与任务作业列表里已完成的所有任务路线是否存在相同的节点或节点区间,若存在则引入时间窗进行冲突判断。 若存在相同节点i,节点i处时间窗满足以下条件则无冲突: to(i)≠tn(i) (8) 若存在相同的i-j节点区间,i-j节点区间的时间窗满足以下条件则无冲突: Startn>Endo||Endn (9) step4在当前任务的所有最短路线依次执行时间窗冲突检测过程中,若发现一条最短路线无冲突则停止剩余最短路线的时间窗冲突检测,将这条路线作为该任务的最短可行路线,跳转到step6。若所有的最短路线都存在冲突,则将其中一条路线中的冲突节点临时作为障碍节点处理,改变邻接矩阵,转到step5。 step5循环step2~step4,直至得到无冲突的最短路线,释放临时障碍节点,完成对当前任务的规划。 step6循环step2~step5,直到任务列表中的作业任务全部规划完成。每当无人机到达该任务航线的目标节点时,该任务在任务列表中自动消除[28]。 为验证上述算法的可行性,结合实例应用Matlab进行算法验证。执行作业任务时的带权路线图如图1所示。 图1 带权路线图 图1中包括8个节点,权值代表2个节点之间的直线距离,如节点1和节点2间的长度为20米。假设在t=0 s,t=10 s,t=20 s时刻依次生成Task1、Task2和Task3这3个作业任务,指定任务优先等级Task1>Task2>Task3。作业任务包括:Task1起始节点为节点1,目标节点为节点6;Task2起始节点为节点6,目标节点为节点1;Task3起始节点为节点3,目标节点为节点8。其中U1、U2和U3为3架空闲的无人机,分别停在节点1、节点6和节点3。为了方便上述改进算法的验证,假设作业任务生成时空闲的无人机U1、U2和U3均能被各个任务随时调配使用。 根据图1构建8×8的邻接矩阵A0: 运用改进Dijkstra算法对上述任务集合进行规划,生成的变长回溯数组如表1所示。 表1 变长回溯数组 根据各任务生成的回溯数组,查询到各任务包含总长度相等的全部最短可行路线如表2所示。 表2 Task1、Task2、Task3任务路线 由表2可知,运用改进Dijkstra算法对上述的3个作业任务规划出来的可行路线结果为:Task1有2条最短路线,Task2有2条最短路线,Task3有1条最短路线。由于优先等级Task1>Task2>Task3,Task1选择其中1条最短路线1→4→7→6作为最终路线,则Task2第1条最短路线6→7→4→1和第2条最短路线6→5→2→1的任务路线时间窗分别与Task1任务路线时间窗做冲突检测,结果如图2所示。 图2 Task1、Task2任务路线时间窗 由图2中Task1和Task2任务路线的时间窗冲突检测可知,Task2的第1条最短路线的时间窗与Task1路线的时间窗在20 s-50 s的时间区间内同时占用了4-7节点区间,说明Task2的第1条最短路线与Task1的任务路线在4-7节点区间内发生了区间类型冲突;Task2的第2条最短路线时间窗与Task1路线的时间窗不存在冲突,在算法执行过程中,Task2选择规划的第2条最短路线6→5→2→1作为最终路线。 以上得到了Task1和Task2的任务路线,由表2可知,Task3只规划出一条最短路线3→6→8,Task3与Task1、Task2任务路线的时间窗冲突检测结果如图3所示。 图3 Task1、Task2、Task3任务路线时间窗 由图3各任务路线的时间窗冲突检测可知,Task3任务路线与Task1任务路线第60 s时在节点6处发生了节点冲突,由于任务优先等级Task1>Task3且Task3没有备用的最短路线可选,在算法执行过程中,将节点6作为Task3的临时障碍节点处理,即3-6节点区间视作为禁行区间,更改邻接矩阵,将a36和a63改为∞,对Task3重新规划路线,邻接矩阵更改为A1。 更改邻接矩阵后,Task3任务路线的变长回溯数组也跟随发生改变,生成的变长回溯数组如表3所示。 表3 变长回溯数组 回溯数组的改变使规划的路线发生相应的改变,根据生成的回溯数组,查询到Task3任务的最短路线如表4所示。 表4 Task3任务路线 由表4可知,Task3更改为2条最短路线,第1条最短路线为3→4→7→6→8,第2条最短路线为3→2→5→8,Task3与Task1、Task2任务路线的时间窗冲突检测结果如图4所示。 图4 Task1、Task2、Task3任务路线时间窗 由图4可知,更改邻接矩阵后,Task3的第1条路线与Task1和Task2的任务路线没有发生冲突。由于第1条路线无冲突,算法执行过程中不会再对第2条路线进行时间窗冲突检测,因此Task3选择规划的第一条最短路线3→4→7→6→8作为最终路线。 通过对整个任务集合中的作业任务进行路线规划,实验结果可以看出,在保证各任务路线互不冲突的前提下,Task1与Task2都选择了长度最短路线,Task3选择了次优路线,说明经过算法改进后,在多无人机执行作业任务时,能够解决任务集合中可能面临的路线冲突问题并规划出各任务之间互不冲突的最短可行路线,对任务集合进行规划的效率有了明显提高。 面对经典Dijkstra算法在进行多无人机执行任务路线规划时,其规划的结果只能给出各任务的一条最短可行路线且不会考虑各任务执行过程时可能存在的路线冲突问题,本文提出了一种改进Dijkstra算法的多无人机寻找防冲突最短路线算法。在由当前任务的起始点逐步向目标点搜寻的过程中,通过引入变长回溯数组来得到各任务包含总长度相等的全部最短路线,再引入时间窗冲突判断模型从各任务的所有最短路线中找出互不冲突的可行路线,若所有路线都冲突,则将冲突节点临时视作障碍点处理,通过改变邻接矩阵得到回溯数组来重新查询任务路线,再次引入时间窗冲突判断模型来得到与其他任务互不冲突的可行路线。 仿真实验表明该算法能够规划出各任务包含总长度相等的全部最短路线且能判断出各任务路线之间是否存在冲突,能够有效解决任务执行时存在的节点类型冲突和区间类型冲突,当与所有最短路线都存在冲突时,还能为该任务规划出次优路线,对作业任务集合的规划效率有着明显提升。本文仅针对3个作业任务进行了仿真验证,且同时也适用于多个任务的情况。2 改进Dijkstra算法引入时间窗
2.1 时间窗
2.2 改进Dijkstra算法引入时间窗模型步骤
3 算法的验证
3.1 作业任务描述
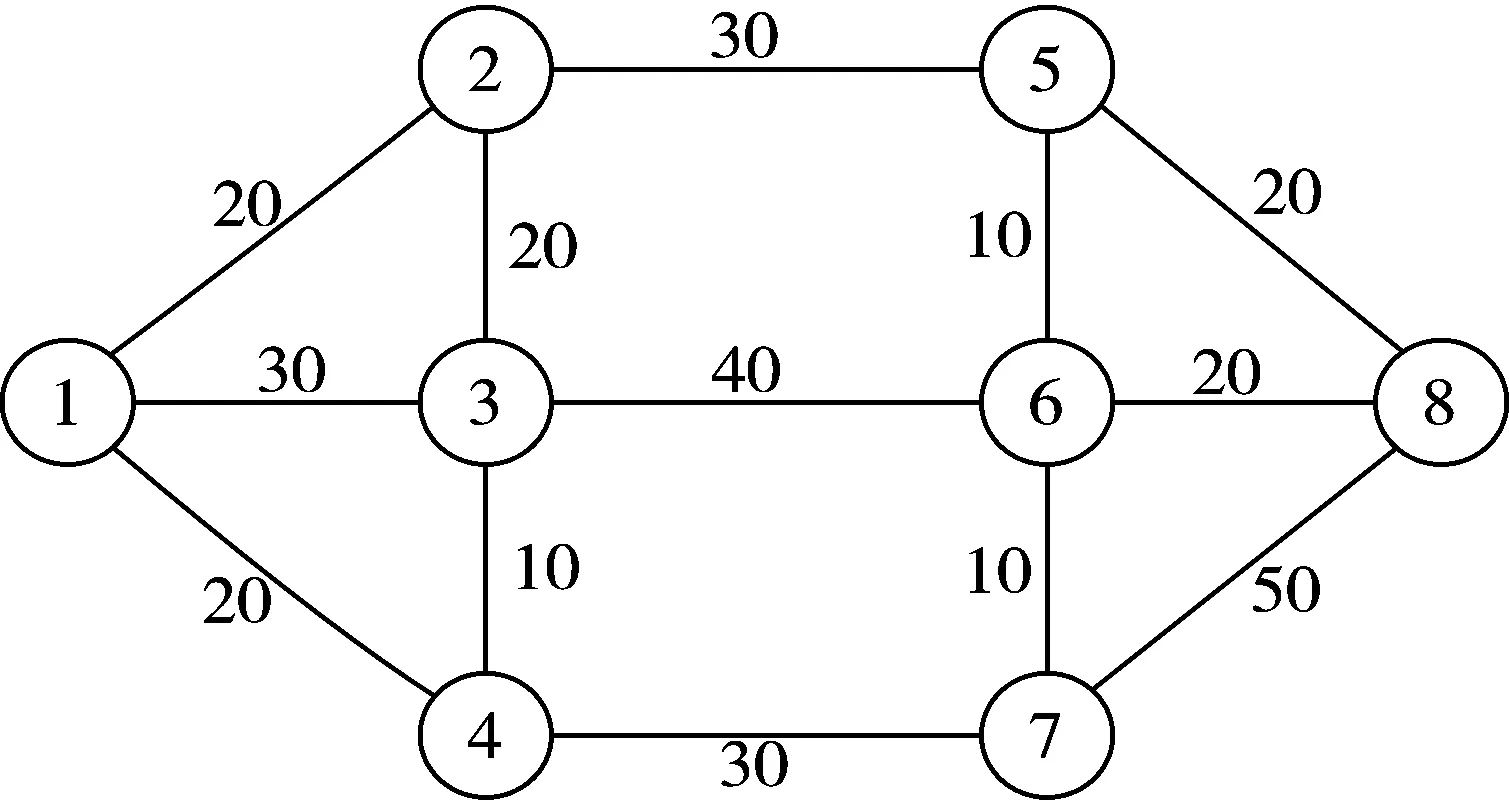
3.2 方案验证

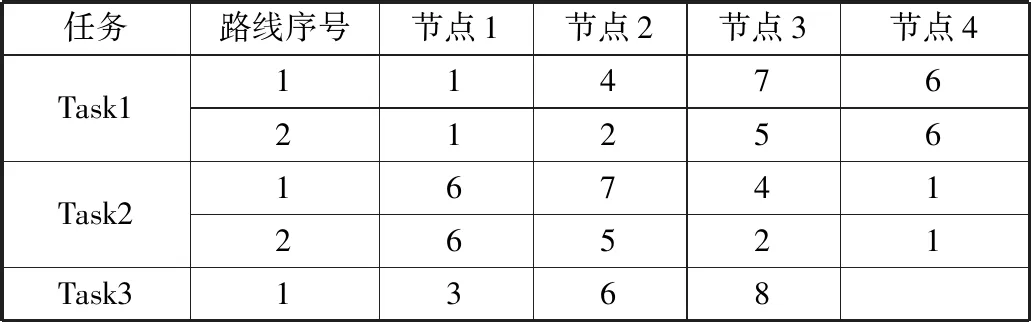
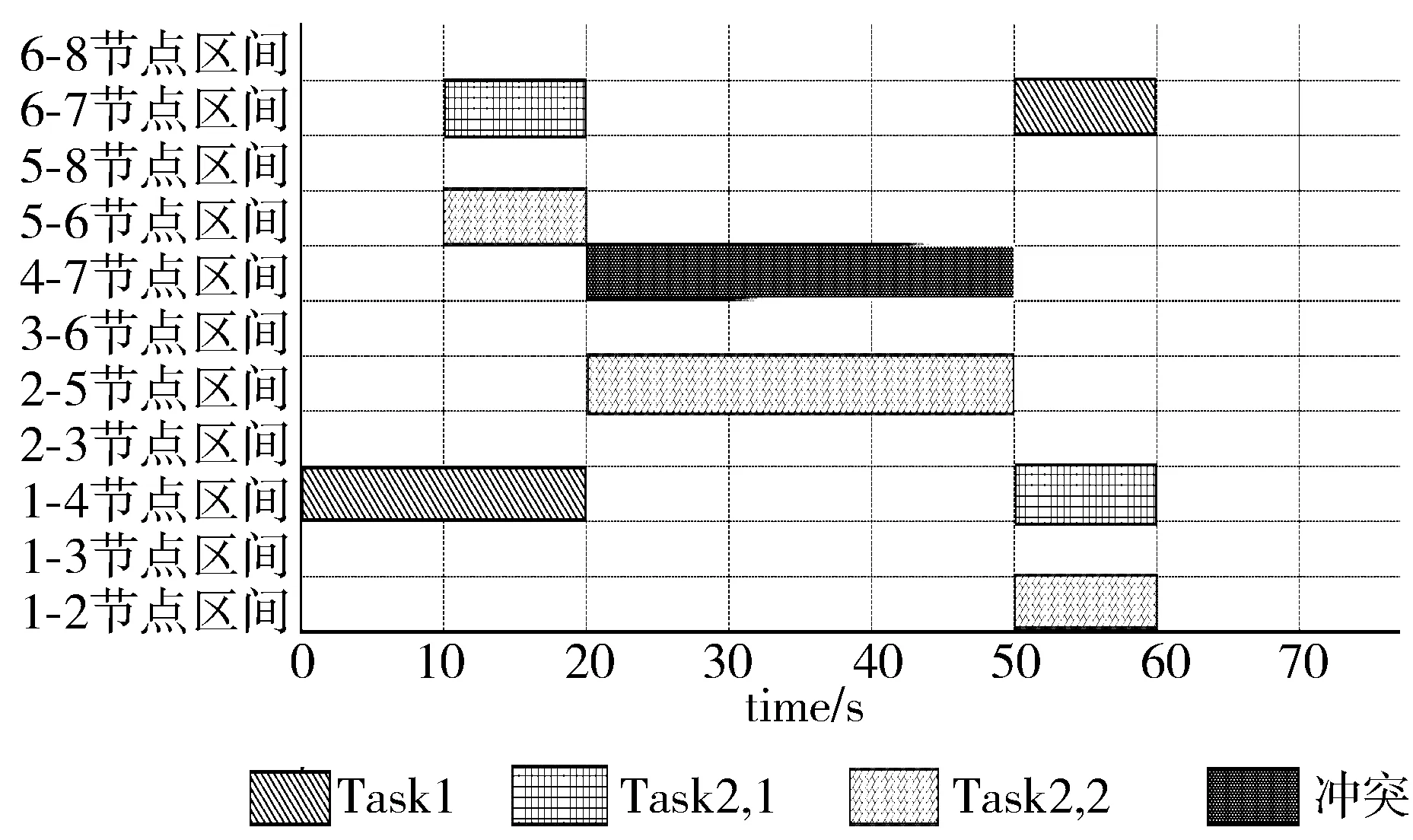
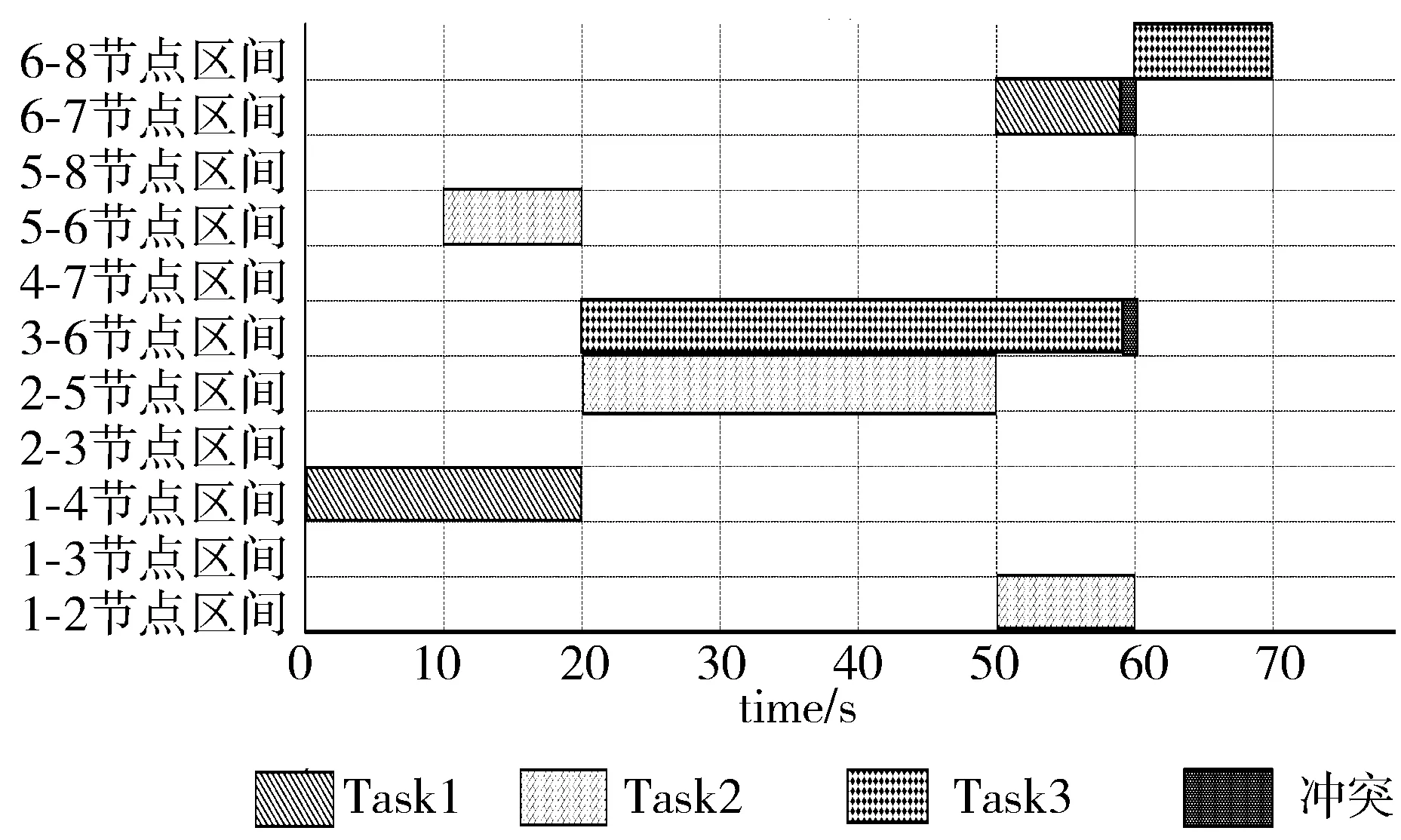


4 结束语
