承轨台与道床板相对高差对轨道结构静力学特性影响

黄 辉，尹华拓，罗信伟，曾志平，肖燕财

(1.广州地铁设计研究院股份有限公司，广东 广州 510010)(2.中南大学土木工程学院，湖南 长沙 410075)(3.中南大学重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

轨道结构作为轨道交通工程的重要组成部分，对其各项参数的研究受到国内外研究人员青睐，如狄怡霏等[1]建立了桥上无缝线路梁轨相互作用有限元分析模型，确定了有轨电车35 m小半径曲线段桥上无缝线路小阻力扣件刚度的合理取值范围；张政等[2]建立了桥上轨枕板式无砟轨道结构有限元模型，研究了轨枕板外形尺寸及板下垫层厚度对轨道受力与变形的影响；齐燕楠[3]基于静力计算模型，分析了列车在竖向、横向荷载共同作用下，高分子阻尼材料、降噪块、调轨组件、弹性垫板等组件的弹性模量对地铁拼装式轨道系统受力与变形规律的影响；夏志强等[4]利用有限元软件ABAQUS对轮轨耦合动力相互作用机理和轨道振动源强特性进行了研究，探讨了浮置板长度、轨道不平顺、扣件刚度、钢弹簧刚度和行车速度对钢弹簧浮置板轨道动力特性的影响；Zeng等[5]通过建立列车-LVT(low vibration track)结构动力学耦合模型，模拟了LVT不同轨、块的横、竖向刚度下车辆及轨道结构动力学指标的变化规律，得到不同轨道结构刚度最优取值范围。但是，对轨道结构部件空间位置的研究，尤其是对轨枕、道床板等混凝土工程的研究，目前尚没有得到足够的重视。

本文以某地铁工程为背景，在地铁A型车的静载作用下，利用有限元法对轨枕承轨台与道床板顶面之间不同相对高差下轨道结构的力学特性进行分析研究。

1 轨道结构有限元模型

我国的板式无砟轨道通常由底座板、CA砂浆层(或自密实混凝土层)、道床板、轨枕、扣件和钢轨等组成[6-7]。本文着重研究列车静载作用下无砟轨道结构轨枕及道床板的静力学特性，为减小计算成本，对轨道结构模型进行了适当简化，道床板以下部分简化为固定约束，扣件简化为弹簧单元。工况设置时，承轨台与道床板顶面相对高差(以下简称相对高差)范围取10～110 mm，级差为10 mm[8]。轨枕及道床板有限元计算模型如图1所示。以道床板中部两块轨枕所对应的钢轨位置作为竖向、横向、纵向三向荷载加载点，分别对不同相对高差下轨枕及道床板受力情况进行分析。

图1 不同相对高差下轨道结构静力学计算模型

2 模型计算参数

1)列车荷载参数。

列车轴重为17 t，竖向荷载动力系数为2.0，横向荷载为0.8倍静轴重，纵向制动系数为0.25。计算可得每股钢轨荷载作用点竖向荷载为8.5 t×10 m/s2×2.0=170 kN，横向荷载为8.5 t×10 m/s2×0.8=68 kN，纵向荷载为8.5 t×10 m/s2×0.25=21.25 kN。将单转向架作用下扣件节点所受竖向、横向、纵向力计算结果作为轨枕承轨台的荷载输入。

2)钢轨及扣件。

轨道钢轨为60 kg/m的标准轨，采用梁单元进行模拟。钢轨截面面积为77.45 cm2，横、纵向惯性矩Ix和Iy分别为3 217和524 cm4。道床轨道采用DZ Ⅲ型扣件，横、竖、纵向均采用线性弹簧单元模拟。

3)轨枕及道床板。

轨枕、道床板分别为C50和C35混凝土，采用实体单元进行模拟。

无砟轨道结构静力学有限元模型主要材料参数见表1。

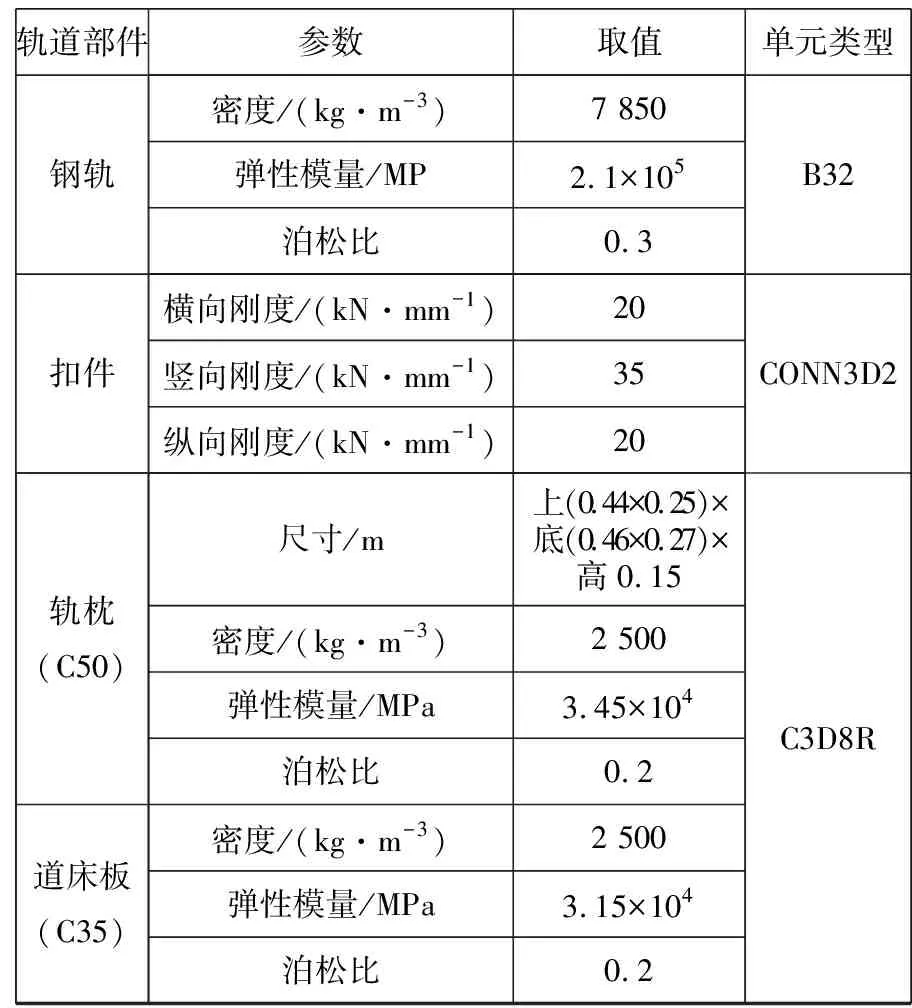
表1 轨道结构静力学有限元模型材料参数

3 不同相对高差下轨枕力学特性分析

3.1 轨枕三向应力分析

在列车静荷载作用下，轨枕最大拉、压应力随相对高差变化曲线如图2和图3所示，由图可知：1)轨枕横向、竖向最大拉应力及变化幅度受相对高差的影响较为显著，各计算工况下，其值分别为0.441～0.992 MPa，0.315～1.239 MPa，变化幅度分别为52.2%、74.6%。轨枕横向最大拉应力随相对高差的增大而减小，竖向最大拉应力随相对高差的增大而增大，纵向最大拉应力幅值波动较小；2)不同相对高差下，轨枕横向及纵向最大压应力变化幅度较为明显，相对差值均大于20%，而竖向最大压应力变化不明显。轨枕横向及纵向最大压应力随相对高差增大而减小，而竖向最大压应力先减小后增大，且在20～100 mm相对高差范围内基本保持不变。

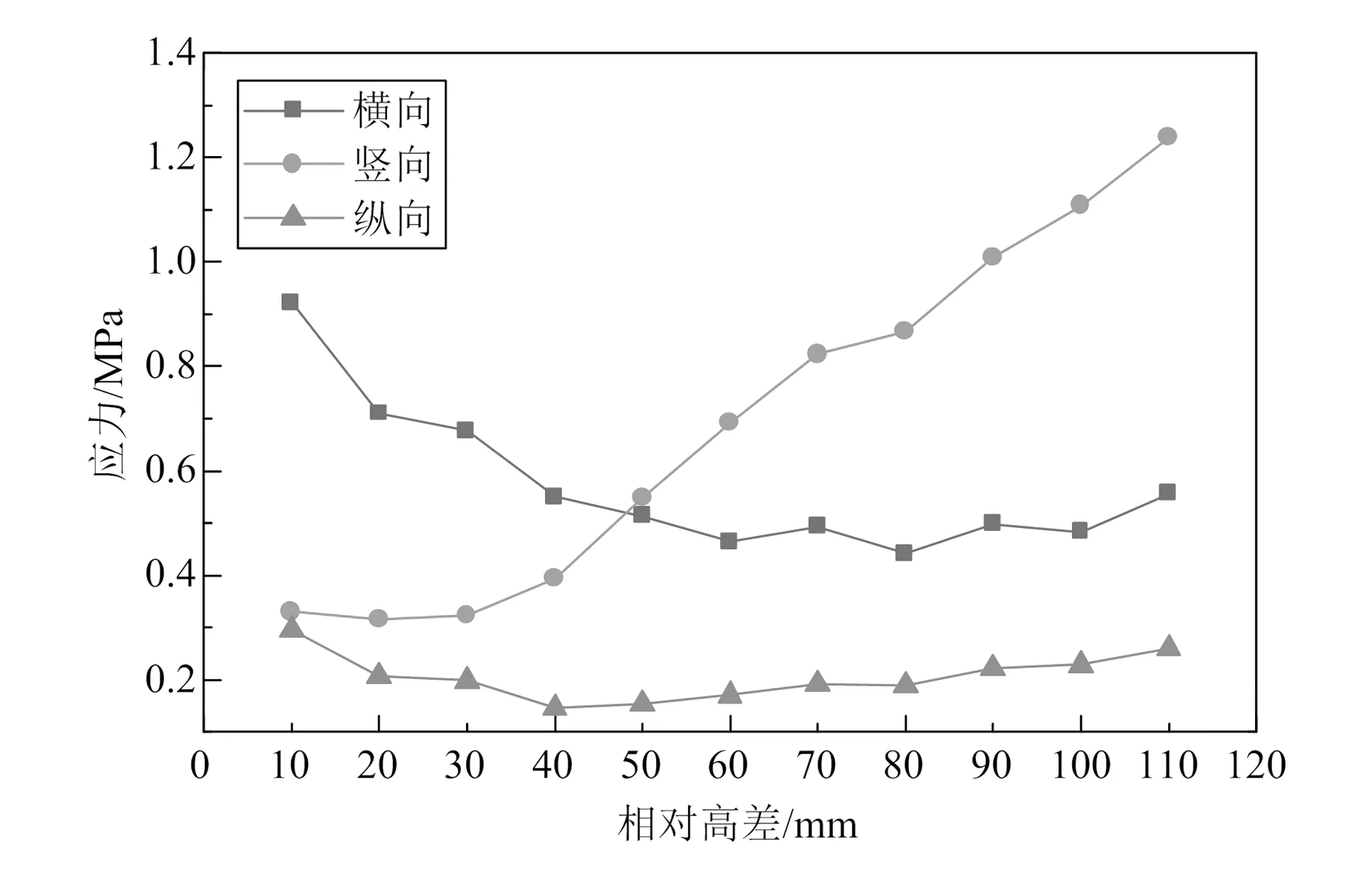
图2 轨枕最大拉应力

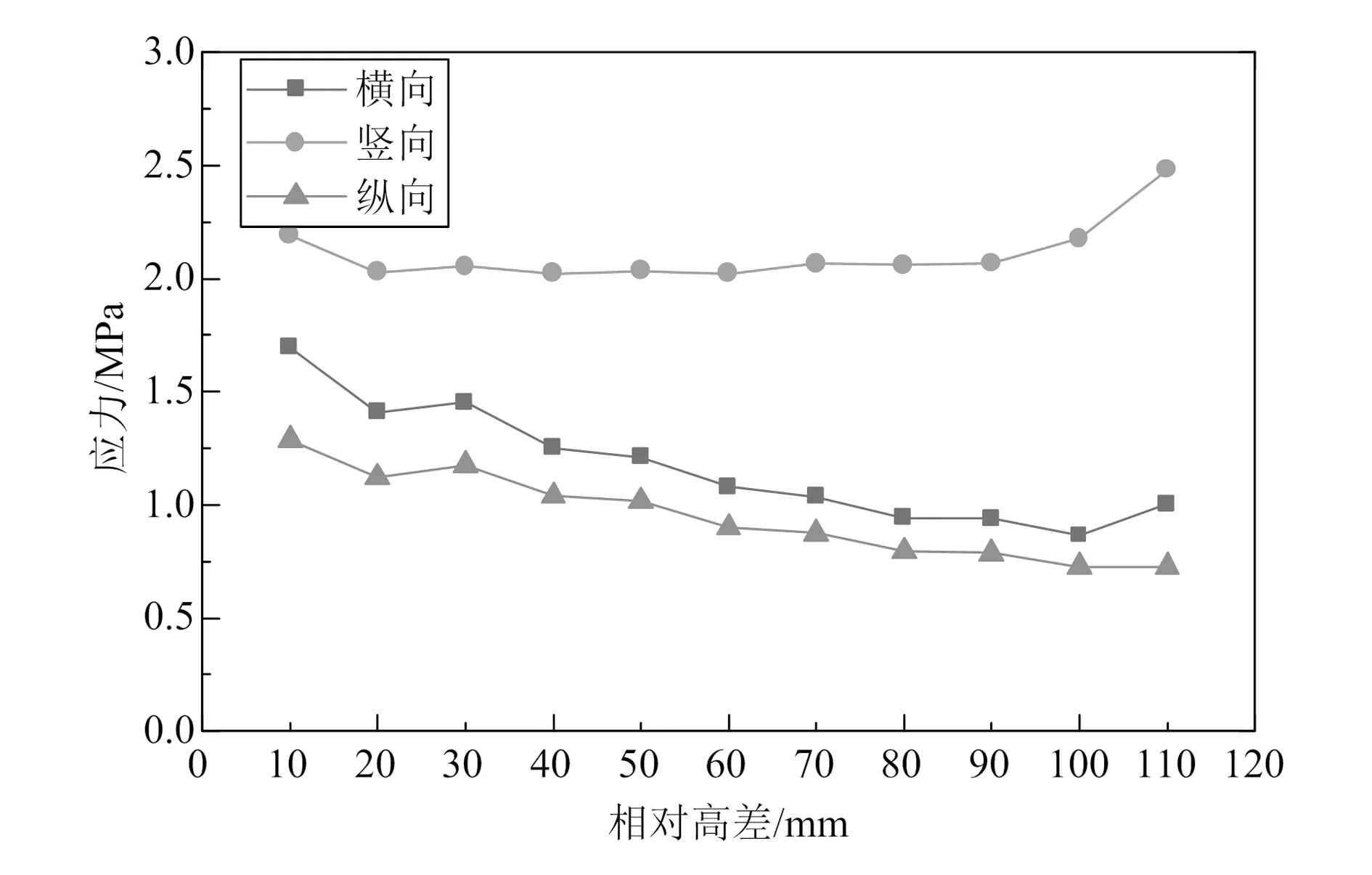
图3 轨枕最大压应力

C50混凝土轴心抗压强度设计值为23.1 MPa，远大于轨枕各向最大压应力；轴心抗拉强度设计值为1.89 MPa，与轨枕最大拉应力较为接近[9]。通常而言，轴心抗拉强度设计值应大于构件的拉应力，方可确保结构安全。为进一步评估轨枕结构的安全性，计算轨枕抗拉强度与最大拉应力之比，绘制其随相对高差变化曲线，如图4所示，由图可知：1)轨枕抗拉强度与最大横向、竖向、纵向拉应力之比值分别为2.05～4.29、1.53～6.00、6.41～12.95，纵向变化最为显著。2)随着相对高差的增大，抗拉强度与横向最大拉应力之比值亦增大，趋于安全，而竖向则相反；抗拉强度与纵向最大拉应力之比先增大后减小，但比值始终不小于6，具有足够的安全性。因此，当相对高差为40～60 mm时，可以保证轨枕抗拉强度与三向应力的比值均保持在较大水平。

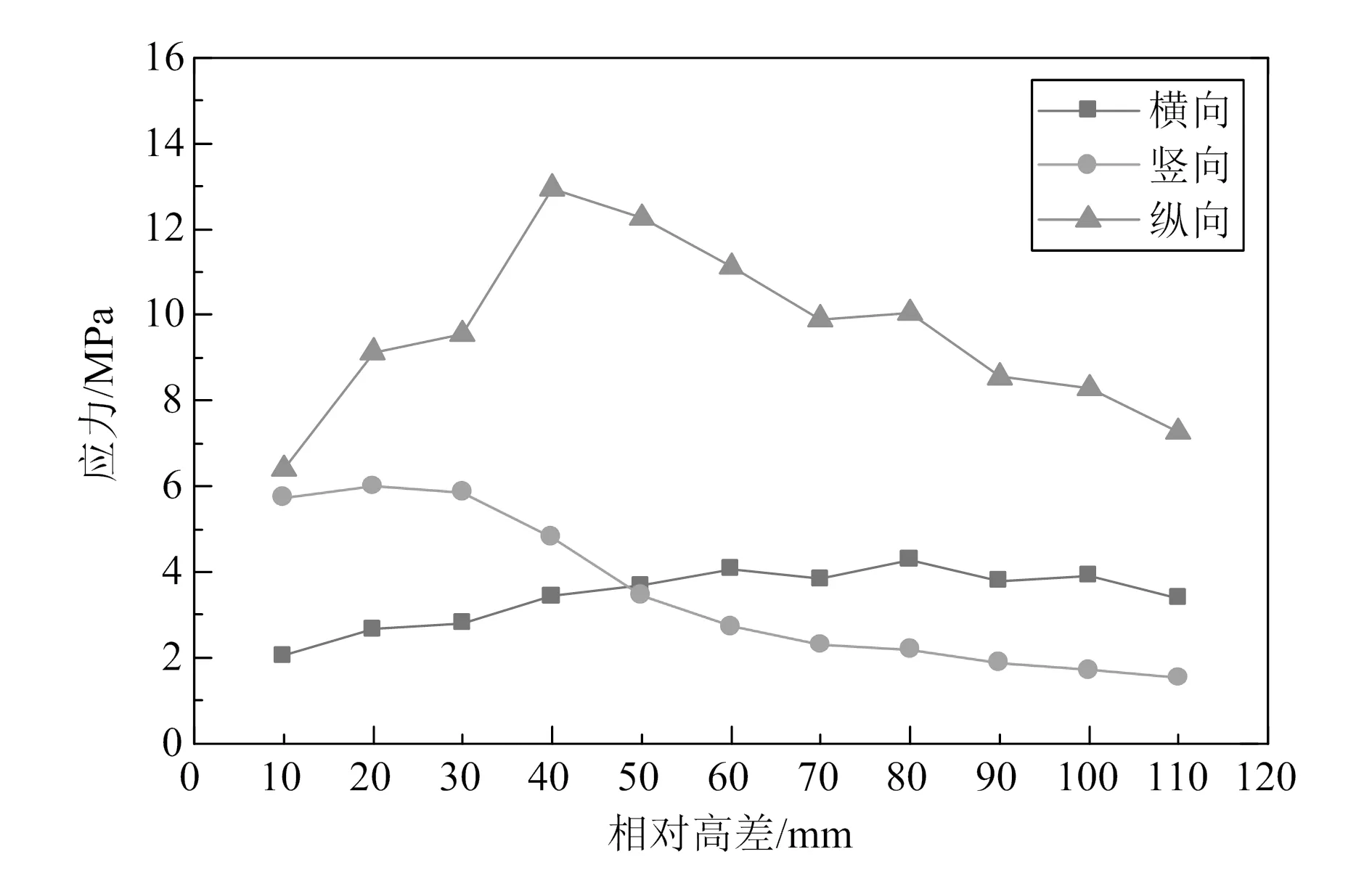
图4 轨枕抗拉强度设计值与最大拉应力之比

3.2 轨枕主应力分析

主应力是研究轨道结构受力的关键因素，依据强度理论，混凝土等脆性材料适用第一主应力，本文简称为主应力[10-11]。不同工况下轨枕主应力随相对高差变化以及轨枕抗拉强度设计值与主拉应力比值变化的曲线分别如图5和图6所示，由图可知：1)轨枕主拉应力、主压应力及变化幅度受相对高差的影响较为显著，各计算工况下其值分别为0.873～1.553 MPa、2.272～3.037 MPa，变化幅度分别为43.8%、25.2%。2)当相对高差增大时，轨枕主拉应力先小幅减小，在相对高差为50 mm后随相对高差的增大而增大；轨枕主压应力先小幅减小，在相对高差为80 mm后随相对高差的增大而增大。与抗压强度相比，轨枕主压应力值较小。3)当相对高差为10～110 mm时，轨枕主拉、压应力均满足混凝土抗拉强度设计值要求，在相对高差约为50 mm时，轨枕抗拉强度与最大主拉应力之比达到最大值。

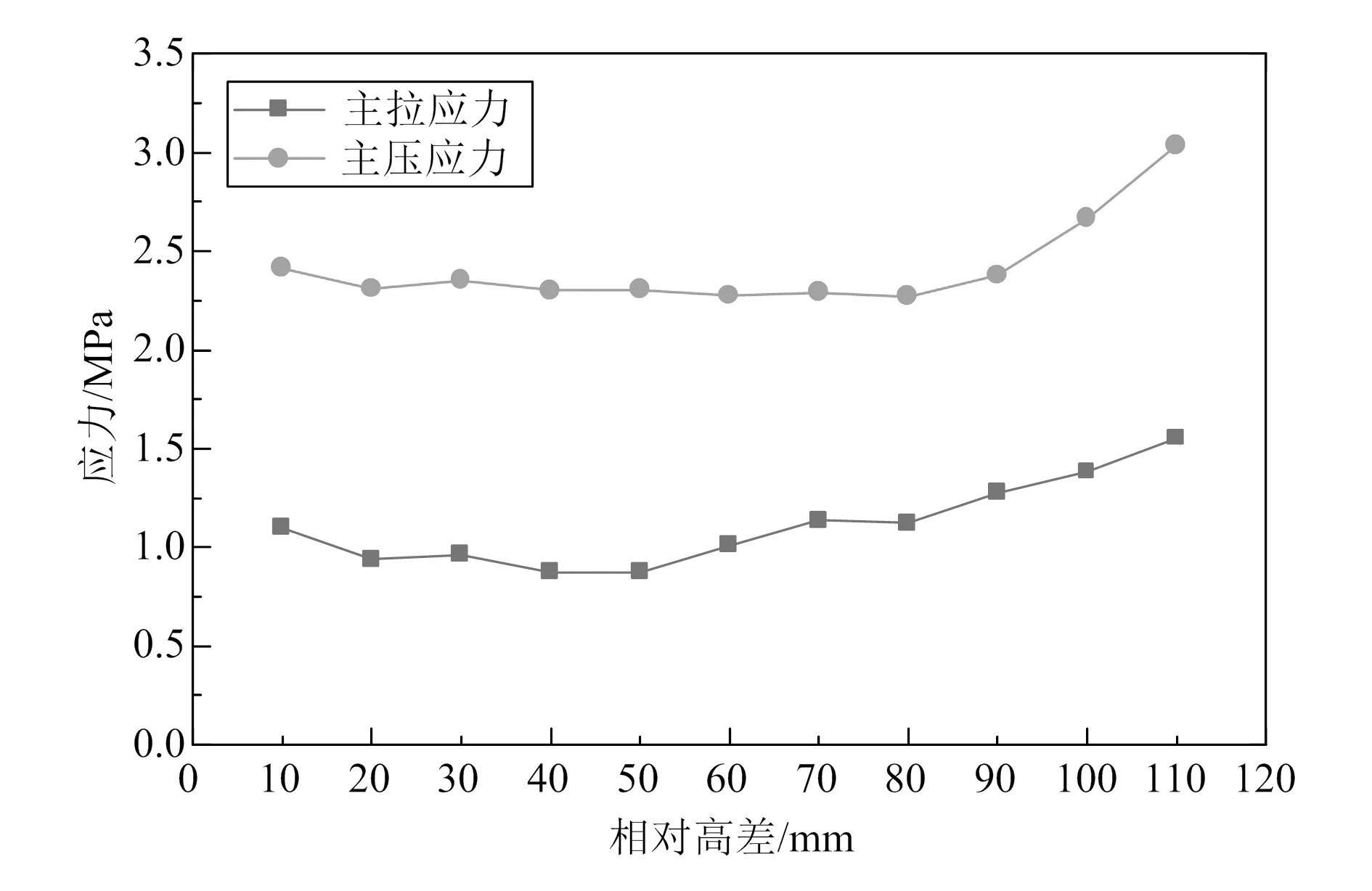
图5 轨枕最大主应力

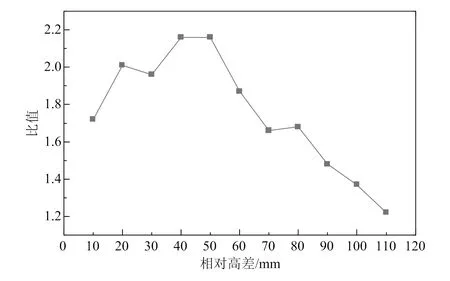
图6 轨枕抗拉强度与最大主拉应力之比

4 不同高差下道床板力学特性分析

4.1 道床板三向应力分析

在列车静荷载作用下，不同工况的道床板最大拉、压应力随相对高差变化曲线如图7和图8所示，由图可知：1)各计算工况下，道床板横向、竖向及纵向最大拉应力的值分别为0.383～0.506 MPa、0.067～0.291 MPa、0.138～0.180 MPa，变化幅度分别为32.1%、77.0%、30.4%。2)各计算工况下，道床板横向、竖向及纵向最大压应力的值分别为0.377～0.828 MPa、0.730～0.967 MPa、0.217～0.505 MPa，变化幅度分别为119.6%、32.5%、132.7%。3)道床板横向、竖向及纵向拉、压应力均随相对高差的增大而增大，横向拉应力、纵向拉应力、竖向拉应力的变化较小，说明轨枕承轨台与道床板顶面相对高差并非拉应力变化的主要影响因素。

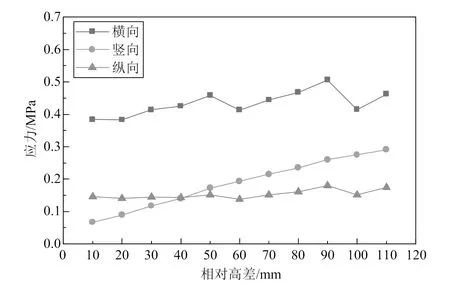
图7 道床板最大拉应力

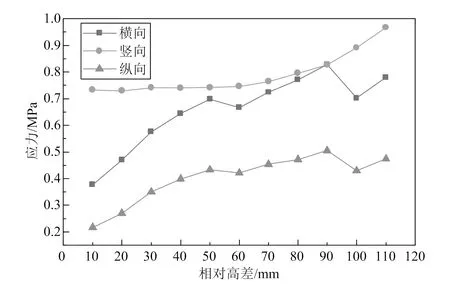
图8 道床板最大压应力

道床板抗拉强度与最大拉应力之比随相对高差变化曲线如图9所示，由图可知：1)当相对高差为10～110 mm时，抗拉强度与道床板最大横向、竖向、纵向拉应力之比值分别为3.10～4.10、5.40～23.43、8.72～11.38。2)抗拉强度与道床板三向最大拉应力之比均随相对高差的增大而减小。其中抗拉强度与最大竖向拉应力之比变化最为显著，但始终大于5，说明在10～110 mm区间内，道床板三向应力均能保持在一个较安全的范围。

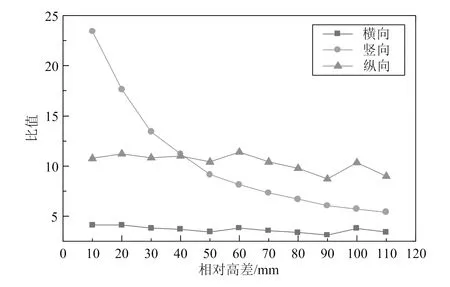
图9 道床板抗拉强度设计值与最大拉应力之比

4.2 道床板主应力分析

道床板主应力随相对高差变化曲线以及道床板抗拉强度设计值与主拉应力比值变化曲线分别如图10和图11所示，由图可知：1)各计算工况下，道床板最大主拉应力、主压应力值分别为0.412～0.676 MPa、0.750～1.231 MPa，变化幅值均为64.1%，二者均满足混凝土强度设计值要求[9]。2)当相对高差增大时，道床板主拉应力随相对高差的增大而增大，与轨枕主拉应力相比，道床板主拉应力幅值较小；道床板主压应力随相对高差的增大而增大，其幅值亦小于轨枕主压应力。其原因在于，列车荷载由轨枕传递至道床板后，受力面积大大增加，荷载迅速扩散。

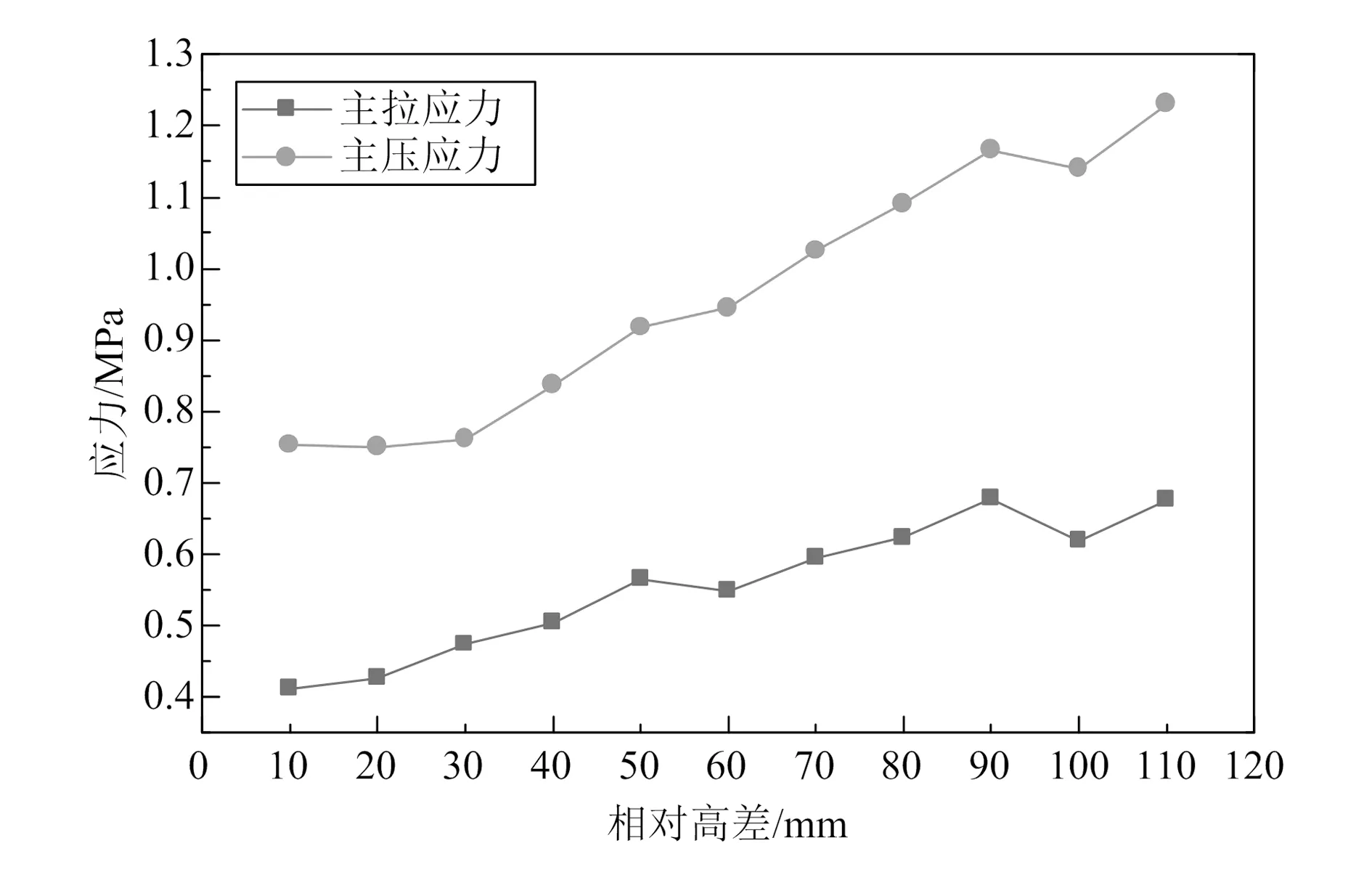
图10 道床板最大主应力

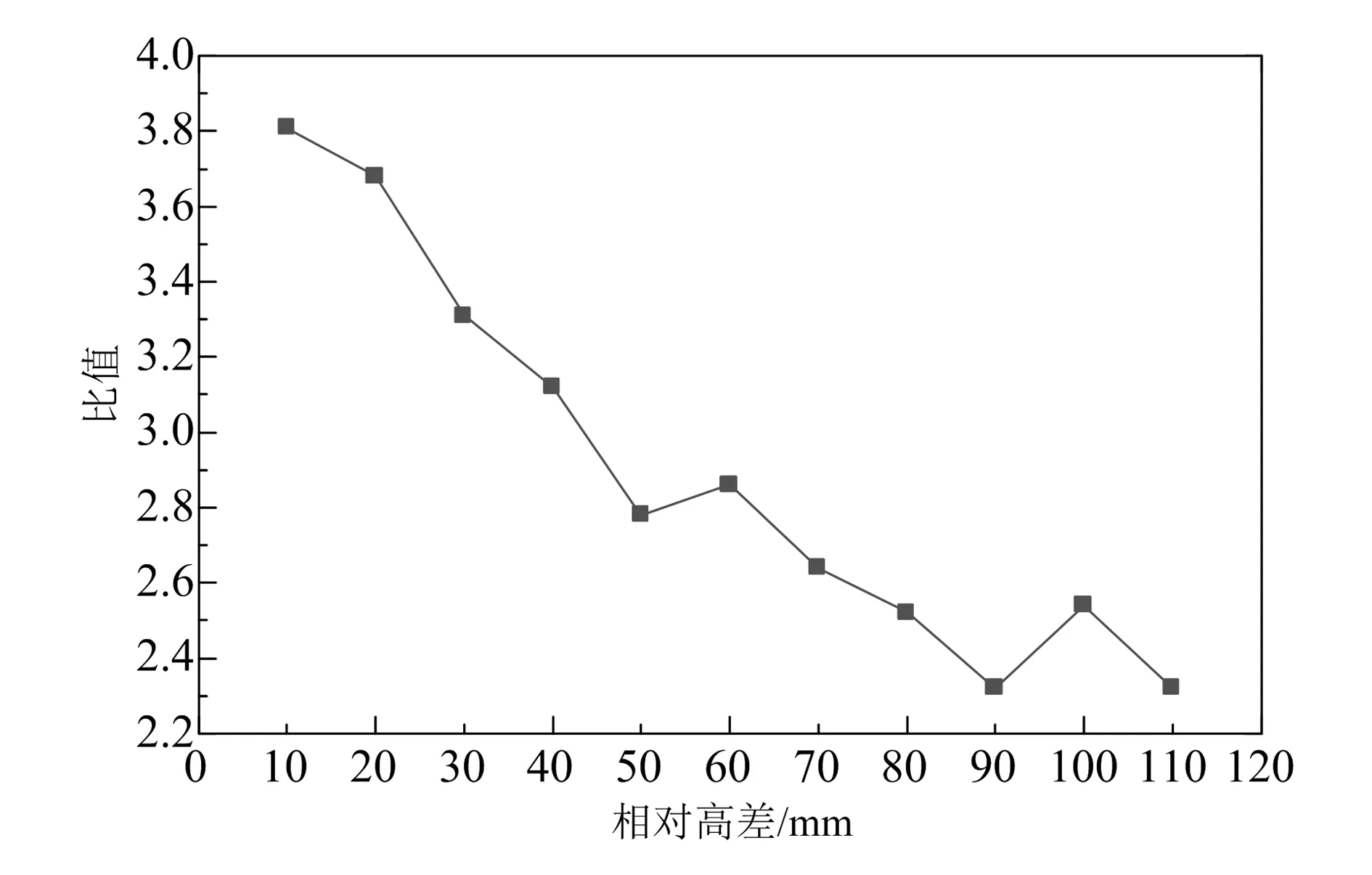
图11 道床板抗拉强度与最大主拉应力之比

5 结论

本文建立了板式无砟轨道的静力学有限元模型，分析了轨枕承轨台与道床板相对高差为10～110 mm时轨枕及道床板的力学特性，得到如下结论：

1)轨枕最大主拉、压应力分别为1.553 MPa和3.037 MPa，道床板最大主拉、压应力分别为0.676 MPa和1.231 MPa，道床板的最大三向应力、最大主应力均小于轨枕。

2)不同相对高差下的轨枕及道床板应力变化分析表明，承轨台与道床板相对高差的施工误差不仅影响轨道的平顺性，对轨道结构受力特性的影响也不容忽视。

3)随着相对高差的增大，轨枕最大主拉应力逐渐逼近抗拉设计强度。综合考虑列车静荷载作用下轨枕及道床板的力学特性，轨枕承轨台与道床板的相对高差约为50 mm为宜。