双梁桥式起重机主梁有限元分析及结构优化
2022-08-18王志斌周国鹏陈国胜
王志斌,张 阳,周国鹏,2,陈国胜
(1.湖北科技学院工程技术研究院, 湖北 咸宁 437100)(2.湖北香城智能机电产业技术研究院,湖北 咸宁 437100)(3.湖北特种设备检验检测研究院咸宁分院, 湖北 咸宁 437100)
桥式起重机是横架于车间、仓库和料场上空进行物料吊运的起重设备,它是目前使用范围最广、数量最多的一种起重机械。主梁是桥式起重机吊运过程中承受载荷最核心的部件,其强度和刚度对于设备的安全稳定运行至关重要。
国内外研究人员针对桥式或门式起重机的主梁做了大量的静力学、动力学研究。2015年Zrnic' 等[1]运用有限元和解析相结合的方法求解了弹性悬挂运动体作用下门式起重机系统的横向和纵向振动。2017年 Delic' 等[2]利用CATIA软件建模,并分析了双梁桥式起重机危险工况下整体的静态特性。2018年易朋兴和马德扬等[3-4]研究了不同的约束条件对主梁垂直静挠度的影响,研究得出,与主梁两侧施加约束相比,在主梁两侧下端面施加约束更接近实际。2020年李荣强等[5]通过对主梁进行分析,指出纵向加劲肋对主梁结构有着不可忽视的影响。上述研究中,为了简化研究模型,研究人员通常不考虑端梁,忽略主梁与端梁间搭接或对接的连接约束特性对主梁挠度的影响,直接将简支梁约束施加在主梁两端的不同位置,这种约束方式与实际约束情况存在一定差异,可能导致分析结果出现一定偏差。
在主梁的结构优化方面,2015年唐辉等[6]综合利用ANSYS和Isight,以拉丁超立方设计、BP神经网络、Hooke-Jeeves算法为理论基础,提出一种主梁截面优化设计方法。同年叶青林等[7]采用粒子群算法结合惩罚函数,建立了主梁优化设计的数学模型,对主梁截面尺寸进行了约束优化设计。2019年梁其传等[8-9]针对主梁截面提出了一种结合稀疏网格模型与MOGA算法的优化方法,可使主梁减重9.6%。2020年秦东晨等[10]依据有限元理论和拓扑优化思想,通过编写的MATLAB程序实现箱形梁的拓扑优化,使箱形梁结构整体刚度得到提高。综上,在主梁的结构优化方面,上述研究人员主要从截面参数优化、整体构型拓扑优化两方面着手,针对主梁腹板的拓扑优化研究较少。
为此,本文拟建立包含主梁和端梁间连接特性的简化桥架有限元分析模型,通过将约束施加于端梁,更真实地反映了主梁所受约束的情况;同时通过对主梁腹板进行拓扑结构优化实现主梁腹板的轻量化,为桥式起重机的结构设计与校核提供参考。
1 主梁静挠度工程计算
1.1 基本参数
桥架是桥式起重机的基本构件,由主梁、端梁以及走台等组成。桥架沿高架轨道纵向运行,起重小车沿桥架上的导轨横向运行,提升机构沿铅锤方向升降,形成的工作空间为长方体。本文研究对象为QD75 t-31.5 m-A3双梁桥式起重机,其制造材料为Q235,主要参数见表1。
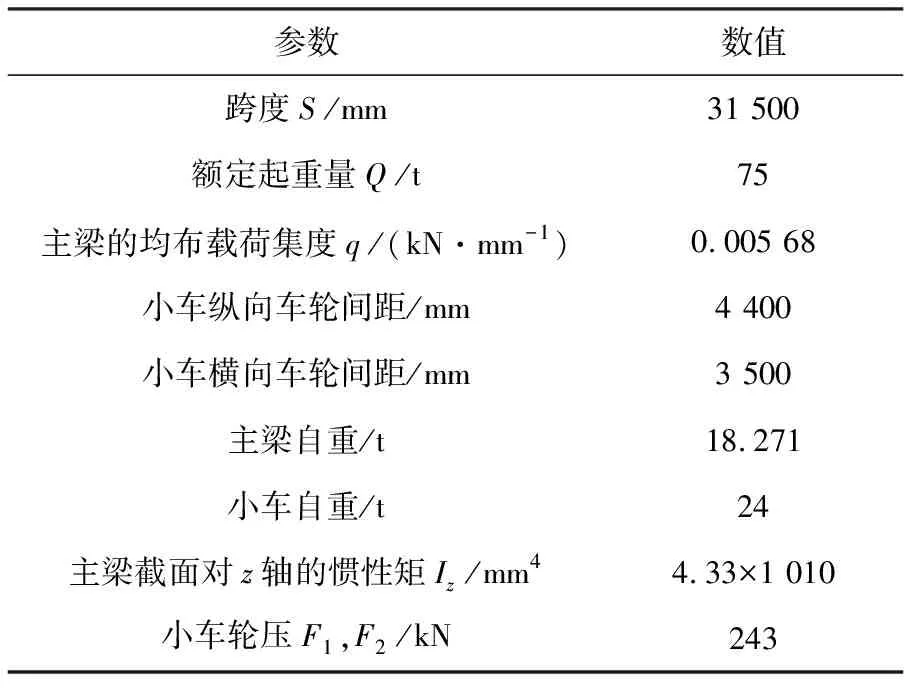
表1 QD75 t-31.5 m-A3双梁桥式起重机主要参数
其主梁属于正轨箱型梁,截面形状如图1所示。图中:t1=20 mm,为设计翼缘板厚;t2=8 mm,为腹板厚度;C=800 mm,为翼缘板宽度;D=720 mm,为主梁腹板间距;H=2 000 mm,为腹板高度。

图1 QD75 t-31.5 m-A3双梁桥式起重机的主梁简化截面
1.2 静挠度工程计算
假设主梁的质量均匀分布,忽略小车轮压差异,主梁主要承受均布的重力载荷和小车轮压集中载荷,将主梁的约束简化为简支梁约束,力学模型如图2所示。图中,F1与F2为由于小车自重及额定起重量产生的小车轮压,a1,b1与a2,b2分别为F1与F2的作用点距两端点A、B的距离,q为主梁均布重力载荷,c为小车的横向车轮间距,S为桥式起重机的主梁跨度。
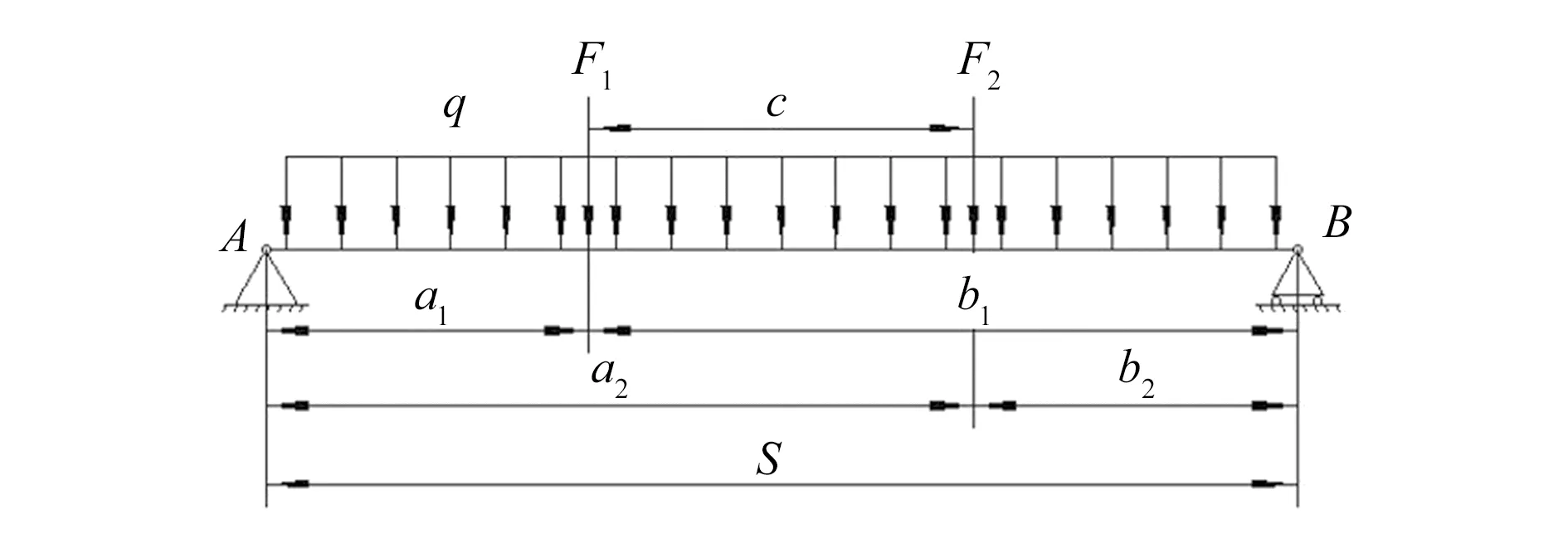
图2 主梁的简支梁模型
在F1,F2及q单独作用下,对应主梁的跨中挠度ω1,ω2和ω3分别为[11]:
(1)
(2)
(3)
根据弯曲变形的叠加法[11],F1,F2及q共同作用时的最大挠度ω为:
ω=ω1+ω2+ω3
(4)
当起重小车在跨中位置,且起重量为额定载荷的条件下,根据式(4)可计算主梁跨中工况下的最大挠度ω。
2 有限元模型的建立
2.1 双梁桥式起重机主梁分析模型
通常情况下,在主梁有限元分析研究中仅建立主梁模型,并且将简支梁约束直接施加在主梁两侧端部。本文考虑端梁和主梁之间搭接因素的影响,建模时保留端梁,建立简化的桥架模型,将约束施加在端梁底部支撑处,以便获取接近实际情况的仿真结果。以QD75 t-31.5 m-A3双梁桥式起重机为研究对象,运用SolidWorks软件进行建模,如图3所示。
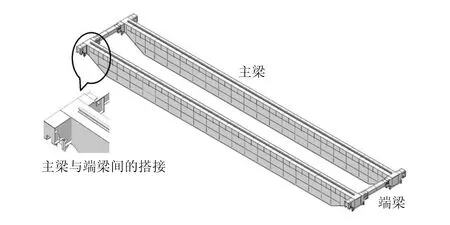
图3 简化桥架的3D模型
2.2 载荷、约束及计算工况
利用ANSYS Workbench的Static Structural模块进行多工况静力学分析,设置材料为Q235,密度为7 850 kg/m3,弹性模量为200 GPa,泊松比为0.3。分析流程如下:
1)导入简化的桥架模型。
2)模型中包含了若干个实体,将实体之间设置为Bond接触类型,形成2 304个接触关系。
3)采用Solid185实体单元划分网格,单元数量为277 118,节点数量为559 136。
4)端梁的大车轮和纵向导轨之间的约束简化为简支梁约束,在大车轮的安装面上添加约束。左侧约束表示约束X,Y,Z方向的移动和X,Y轴的转动(RX,RY),右侧约束表示约束Y,Z方向的移动和X,Y轴的转动(RX,RY),如图4所示。

图4 主梁结构有限元模型及约束条件
5)桥架承受的载荷包括自重载荷和小车轮压形成的集中移动载荷,其中小车轮压包含小车自重和额定起重量。小车运行过程中,主梁导轨承受轮压产生的移动载荷,本文将全过程移动载荷简化为7种小车处于不同位置的工况加载进行静力分析,从距离主梁的简支约束一侧3 500 mm处开始加载,间隔3 500 mm加载一次,共计算7次。
3 仿真结果与分析
3.1 主梁应力与挠度校核
通过对7种工况的计算分析可知,工况4为应力最危险工况,主梁应力分布如图5所示。

图5 跨中工况主梁应力分布
从图5可以看出,主梁最大应力为114.95 MPa,满足最大应力不高于许用应力235 MPa/1.48≈158.78 MPa的要求。由于在主梁腹板和端梁的上下翼缘板接触位置的局部应力集中,该部位最大接触挤压应力为279.97 MPa,易造成疲劳损伤,设计时需局部加强。
最危险工况下,主梁弯曲变形如图6所示。

图6 跨中工况主梁弯曲变形
从图6可以看出,主梁的最大挠度为39.703 mm,出现在跨中位置,满足GB/T 14405—2011通用桥式起重机中最大挠度的要求:不超过S/750≈42(mm)[12]。
3.2 合理性验证
将7种工况下主梁最大挠度的理论计算结果与本文包含主梁及端梁的主梁挠度仿真结果进行对比,如图7所示。

图7 理论与仿真最大挠度对比
从图7可以看出,本文仿真挠度结果略低于理论计算结果,主要原因是理论计算时公式中的截面抗弯惯性矩是由简化截面计算,较真实值偏小,导致理论计算得出的挠度值较真实值偏大7.84%~10.36%,即本文仿真模型及约束方式与实际更为接近,得到的挠度值更准确。
4 结构优化
4.1 主梁腹板拓扑优化
结构优化分为尺寸优化、形状优化、形貌优化和拓扑优化。以材料分布为优化对象,采用拓扑优化可以在均匀分布材料的设计空间中找到最佳的分布方案。在Workbench软件中,拓扑优化在静力学分析或模态分析的基础上进行;进入Topology Optimization分析模块中,首先设置优化区域、优化目标以及约束条件等等,然后进行求解计算,最后查看优化分析的仿真结果。
基于主梁的7种工况静力分析结果,选择主梁的腹板为优化对象,其边界侧面不优化,设置对称约束,以最大刚度为优化目标,设置保留腹板质量80%为响应约束,进行拓扑优化分析,结果如图8所示。
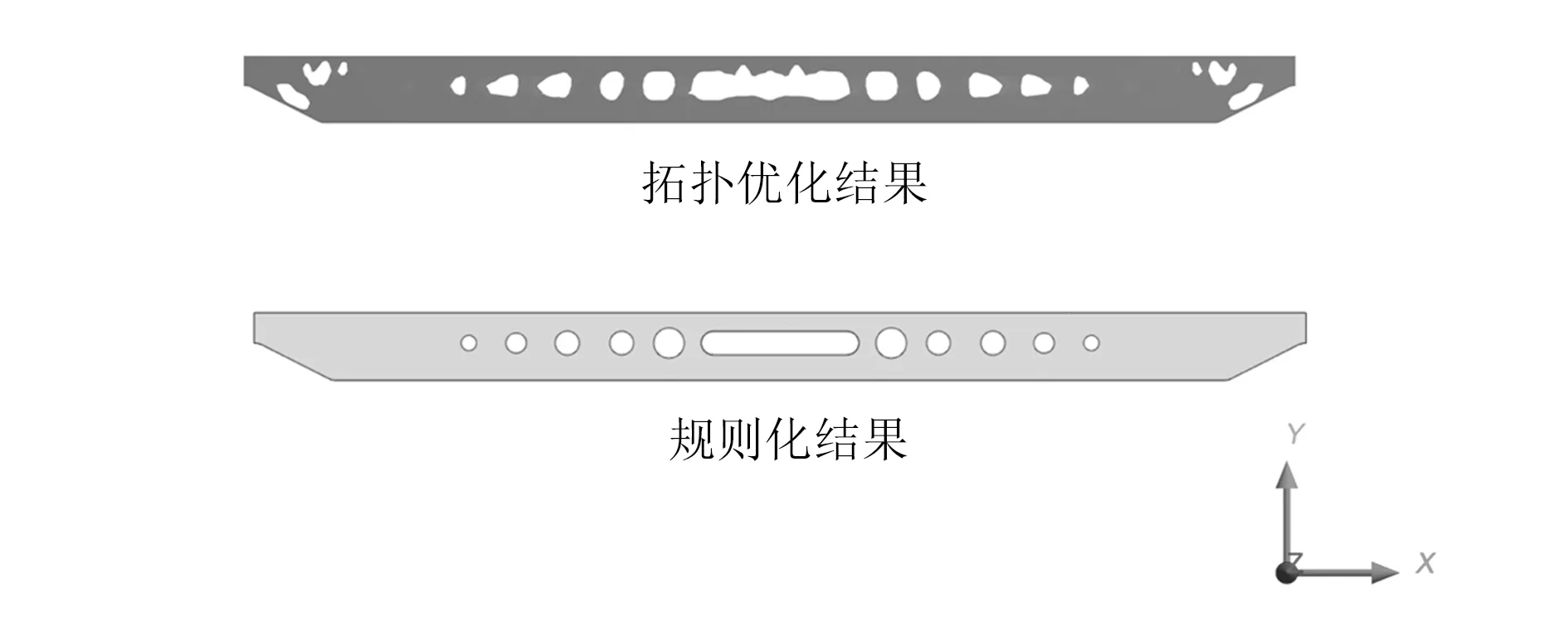
图8 腹板拓扑优化及规则化结构
主梁腹板拓扑优化完成后,腹板结构由一系列不规则的几何轮廓组成,并且存在尖角等可能导致应力集中的几何特征,如图8所示。因此,需要将几何轮廓规则化,并且规则化的几何轮廓边界不能超越不规则的几何轮廓边界。基于腹板两侧的连接关系和受力特点,为避免削弱主梁的性能,基于仿真结果,结合实际情况进一步对腹板结构进行规则化,如图8所示。优化前后腹板的质量分别为3 725.90 kg和3 294.70 kg,轻量化达11.57%。
4.2 优化前后对比
为验证优化结果的合理性,分别对比优化前后主梁的模态、应力与变形情况。其中优化前后对主梁进行预应力模态分析的结果见表2。

表2 优化前后主梁前6阶固有频率对比 单位:Hz
根据GB/T 14405—2011通用桥式起重机[12]相关要求,桥式起重机主梁的固有频率应不小于2 Hz。从表3可知,优化后主梁对应阶数的固有频率略低于优化前,优化前后主梁的最低阶频率分别为4.02 Hz和3.97 Hz,均大于2 Hz,满足要求。
优化后主梁在7种工况下的最大应力如图9所示。
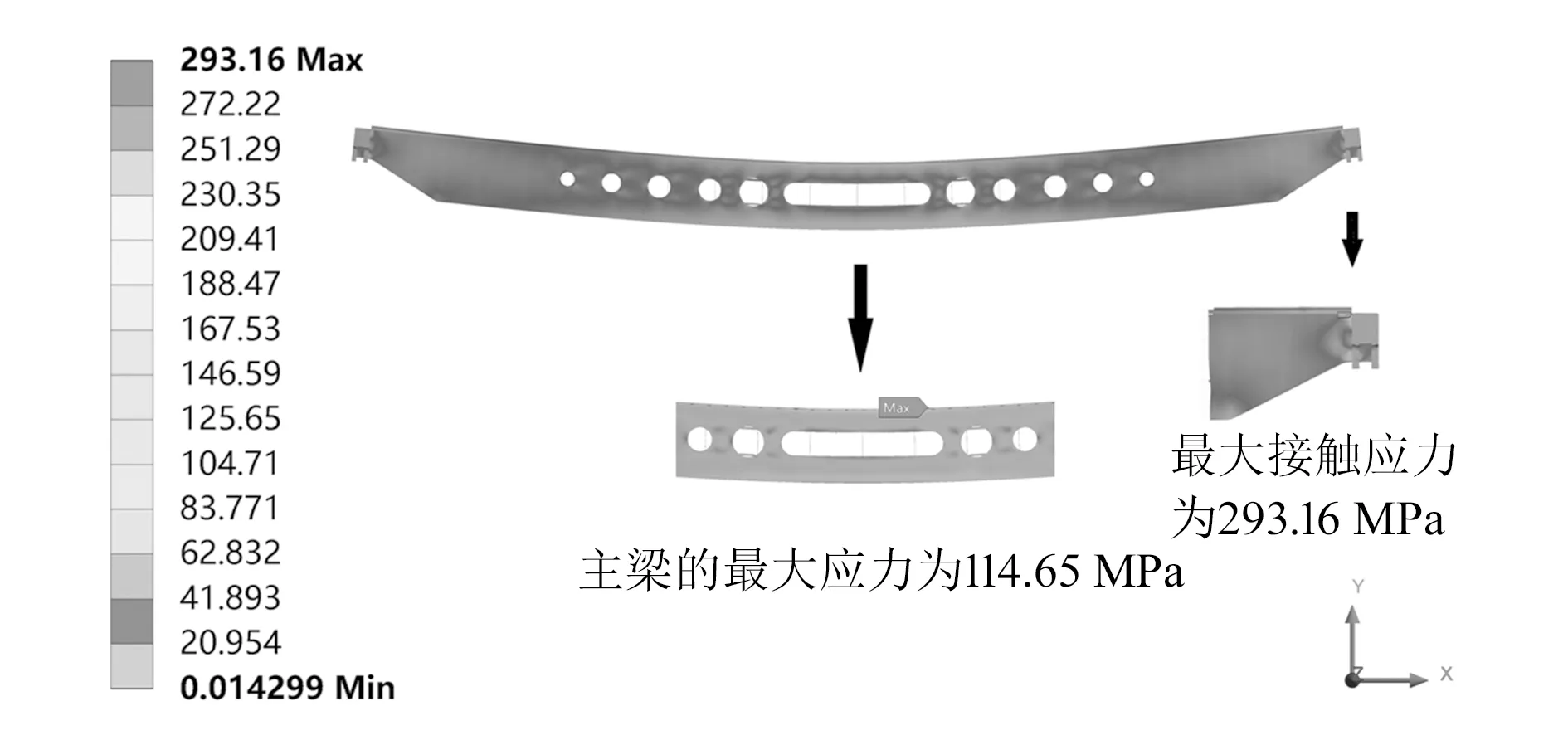
图9 优化后主梁最大应力
由图9可知,优化后主梁的最大应力为114.65 MPa,略低于优化前的114.95 MPa,满足最大应力不超过许用应力158.78 MPa的要求;主梁与端梁结合部位的最大接触应力从279.97 MPa上升至293.16 MPa,即优化后的结构对接触局部的设计优化提出了更高的要求。
优化前后7种工况下主梁最大挠度对比如图10所示。

图10 优化前后主梁最大挠度对比
由图10可知,优化后的最大挠度曲线略高于优化前,优化前后最大挠度分别为39.70 mm与40.20 mm,增幅不超过1.19%,且均低于S/750≈42(mm)。
通过对比分析可知,优化后的主梁腹板在实现轻量化11.57%的同时很好地兼顾了主梁的强度及刚度,即本文的优化方案可为工程设计提供参考。
5 结束语
基于ANSYS Workbench对QD75 t-31.5 m-A3双梁桥式起重机主梁进行了多工况静力学分析及主梁腹板的拓扑优化。结果表明:
1)由于截面惯性矩的计算简化,《通用桥式起重机》(GB/T 14405—2011)中的理论计算公式算出的挠度值偏大7.84%~10.36%,本文包含主梁与端梁的模型仿真得出的挠度值更接近真实值。
2)主梁腹板中部区域是轻量化的首选目标,本文提出的优化结构能在保证强度及刚度的前提下实现腹板减重11.57%。
3)由于主梁与端梁之间采取搭接的连接方式,在主梁腹板和端梁的上下翼缘板接触位置易出现局部应力集中现象,导致局部接触应力超标,该部位易产生裂纹和损伤,设计时需考虑局部加强。
