采用深度迁移学习与自适应加权的滚动轴承故障诊断

贾峰,李世豪,沈建军,马军星,李乃鹏

(1.长安大学道路施工技术与装备教育部重点实验室,710064,西安;2.西安交通大学现代设计与转子轴承系统教育部重点实验室,710049,西安)

基于深度迁移学习的滚动轴承故障诊断方法已经成为研究热点[1-3]。该方法通过领域自适应方式,从有标签的滚动轴承训练样本中学习故障诊断知识,迁移知识并识别相似但不同的轴承测试样本中的健康状态信息,其中训练样本称为源域数据集,测试样本称为目标域数据集[4-5]。迁移诊断方法克服了训练与测试样本集必须服从相同分布的问题,提高了故障识别的准确率与泛化性[6-9]。例如:郭亮等[10]提出领域自适应的迁移诊断方法,实现了轴承之间的跨领域诊断;Kumar等[11]基于稀疏深度学习模型,提高了迁移模型的故障识别能力;Yang等[12]结合领域自适应网络与伪标签学习,实现了滚动轴承的迁移诊断;Qin等[13]通过构建共享分类器,提高了轴承迁移诊断的准确率;Jiao等[14]构建了残差联合域自适应的轴承迁移诊断方法。

上述迁移诊断方法均假设目标域数据样本与源域数据样本必须具有共同的健康状态[15-17],即闭集诊断,如图1(a)与1(b)中源域数据集A向目标域数据集B的迁移诊断。然而,在工程实际中,目标域数据集不仅包含与源域数据集共有的健康状态,而且往往可能包含在源域数据集中未出现的故障状态,即开集诊断,如图1(a)与1(c)中源域数据集A向目标域数据集C的迁移诊断。在解决闭集诊断问题时,传统迁移诊断方法能够有效实现目标域健康状态的准确识别,如图1(d)所示。但是,当传统迁移方法用于开集诊断时,由于在方法训练时没有额外故障的标记,导致无法识别这些故障,将其错分为其它健康状态,致使诊断精度下降,如图1(e)所示。因此,传统迁移诊断方法无法应对轴承开集诊断的难题。

针对滚动轴承开集诊断问题,可行的解决思路是:在训练中,将额外故障标记为未知故障,进而剔除目标域中额外故障的影响,再利用源域故障信息实现目标域中共有健康状态的识别,最终实现准确的故障分类,如图1(f)所示。

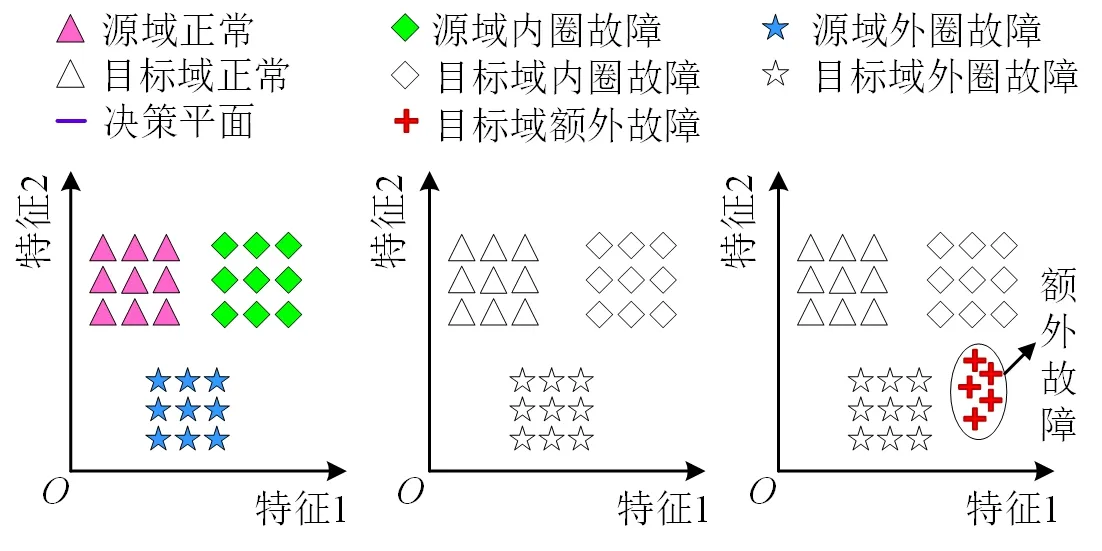
(a)滚动轴承源域数据集A (b)闭集目标域数据集B (c)开集目标域数据集C

综上,本文提出了采用深度迁移学习与自适应加权的滚动轴承故障诊断方法。该方法首先建立特征提取模块,利用深度卷积神经网络将轴承样本映射到高维特征空间;其次,利用迁移学习思想设计加权领域鉴别器,通过对样本进行自适应加权并结合对抗训练,增大目标域与源域共有健康状态样本的领域相似性,抑制目标域额外故障状态样本与源域的领域相似性,进而设定阈值剔除目标域未知故障样本,实现滚动轴承开集迁移智能诊断。最终,利用3个轴承数据集验证了提出方法的有效性。

1 基础理论

领域对抗网络(domain adversarial training of neural network,DANN)由Ganin等[22]提出,通过领域对抗方式增强领域相似性,促使源域与目标域数据在特征空间进行对齐,增强领域数据分布的相似性,实现领域知识的迁移学习。

领域对抗网络主要由3部分构成:特征提取器Gf、领域鉴别器Gd和分类器Gy。首先,特征提取器主要提取数据深层故障信息;然后,利用对抗学习混淆领域鉴别器,达到提升领域相似性的目的;最后,利用分类器进行识别。损失函数为

(1)

(2)

2 故障诊断方法

针对滚动轴承开集迁移诊断问题,引入了共享集与未知集的概念[16],提出了采用深度迁移学习与自适应加权的滚动轴承故障诊断方法。该方法由特征提取模块、训练模块与测试模块构成,如图2所示。其中:特征提取模块利用深度卷积神经网络提取轴承故障特征;训练模块利用迁移学习思想,通过样本自适应加权实现目标域未知故障识别;在测试模块中,将源域故障诊断知识迁移到目标域共有健康状态样本的故障识别中。

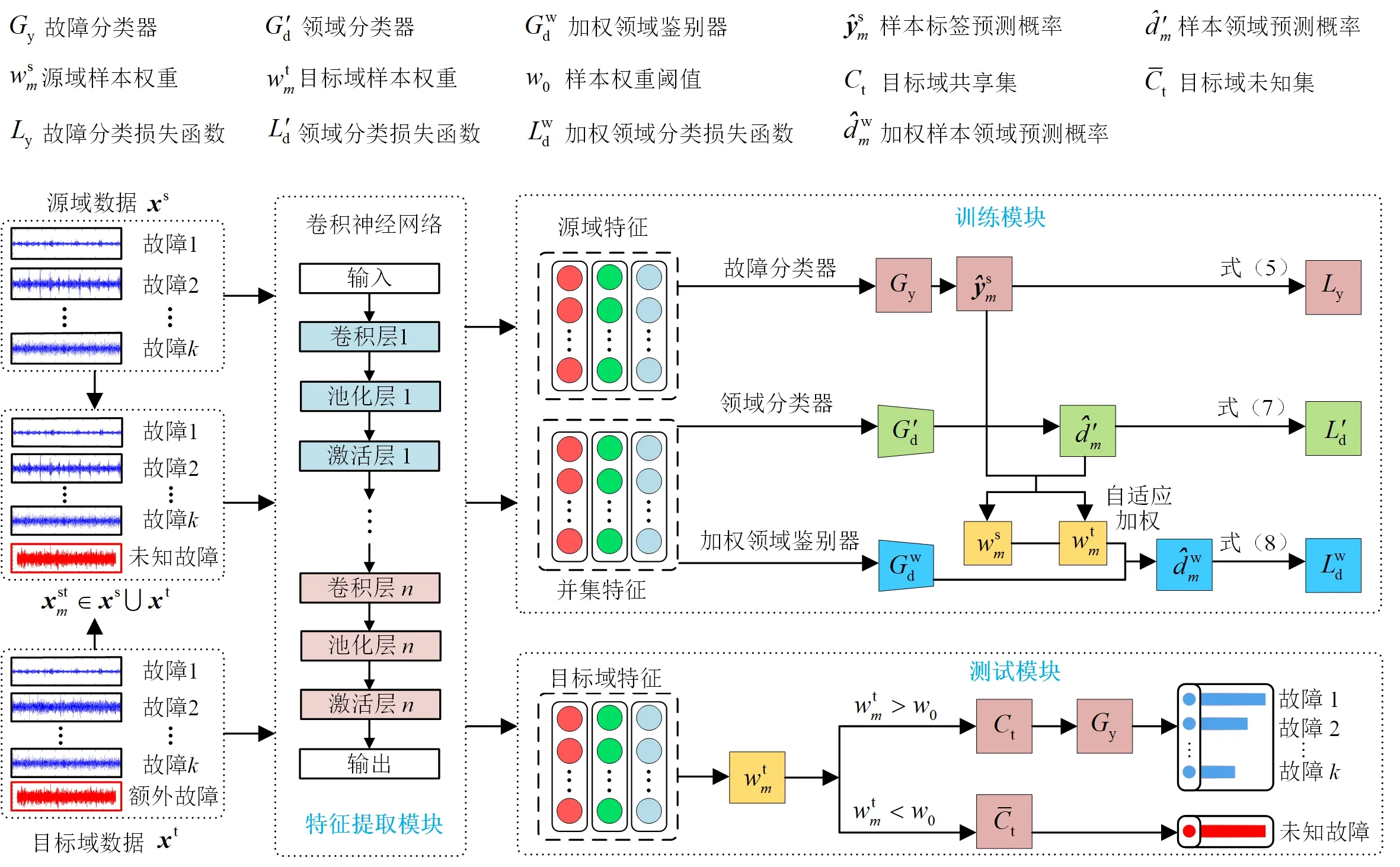
图2 提出的滚动轴承故障诊断方法

2.1 共享集与未知集的定义

2.2 特征提取模块

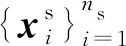
(3)

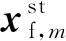
2.3 训练模块

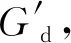
2.3.1 故障分类器

(4)

根据式(4),结合源域特征的真实故障标签,故障分类器的损失函数可表示为

(5)

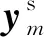
2.3.2 领域分类器

(6)

根据上述领域信息,领域分类器的损失函数表示为

(7)

式中dm表示第m个特征的真实领域标签,当其为0时表示目标域,为1时表示源域。

2.3.3 加权领域鉴别器

识别轴承目标域中未知故障样本的可行思路是[16]:以传统领域鉴别器的对抗训练为基础,在训练过程时,对样本进行自适应加权,通过增大目标域共享集与源域的领域相似性,抑制目标域未知集与源域的领域相似性,控制样本权重所度量的领域相似性程度。再通过设置权重阈值,区分源域和目标域中的共享集样本与未知集样本。因此,参考文献[16],设计加权领域鉴别器,其损失函数如下

(8)

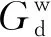
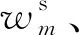
(9)

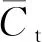
由此可知,若可以利用训练过程中故障分类器的故障预测信息熵与领域分类器的领域预测概率等信息,计算样本权重,自适应匹配出式(9)中样本权重的逻辑关系,则可控制样本的领域相似性程度,进而识别目标域中的未知集样本。

(1)故障预测信息熵。利用该信息熵可度量故障分类器对故障样本识别的确定性。当故障预测信息熵越小时,表明此样本故障标签越容易确定;反之则较难确定。信息熵计算式为

(10)

(11)

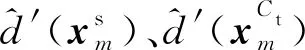
(12)

(3)权重计算方法。依据故障预测信息熵与领域属性预测概率,可得到样本权重计算公式

(13)

式中T表示每次训练时的样本数,使样本故障预测信息熵被归一化至0～1之间,确保其与领域预测概率值在同一尺度下。依据式(11)、(12),可知式(13)计算得到的权重具有关系

(14)

式(14)得到的权重关系与式(9)设计的权重逻辑关系相匹配,因此可通过设置合理阈值,区分目标域共享集与未知集。

2.4 测试模块

在测试模块中,通过设定合理阈值,识别目标域未知集,进而剔除未知样本的干扰,再利用源域数据训练得到的故障分类器对目标域共享集轴承样本进行识别,公式为

(15)

式中w0为区分目标域共享集与未知集的阈值。

2.5 故障诊断方法的目标函数

综合轴承故障分类器、领域分类器及加权领域鉴别器的损失函数,得到诊断方法的优化目标

(16)

在获取滚动轴承源域与目标域监测数据之后,首先使用归一化方法对数据进行预处理,然后采用Adam方法对式(16)进行优化,完成轴承故障诊断方法的训练。

3 实验验证

通过3个案例验证提出的滚动轴承故障诊断方法的有效性。

3.1 案例1:变工况下齿轮箱轴承开集迁移诊断

齿轮箱轴承监测数据采集于如图3所示的故障实验台。该实验台由电机、齿轮箱、磁粉制动器等零部件组成。实验轴承位于齿轮箱输入轴的轴承座内,将加速度传感器吸附在轴承座上方,采集滚动轴承监测数据。

(a)齿轮箱轴承故障实验台

在故障实验中,实验台通过磁粉制动器为系统提供负载,分别在600、1 800 r·min-1两种不同转速条件下采集两组数据,采样频率为5 kHz。根据实验转速条件不同,分别定义为数据集A、B。每个数据集包含4种轴承健康状态:正常(N)、内圈故障(IF)、外圈故障(OF)和滚动体故障(RF),每类轴承健康状态样本为228个,单个样本的数据长度为1 044。针对滚动轴承开集诊断实验,依次剔除数据集A中内圈故障、外圈故障和滚动体故障样本,并定义为A1、A2和A3。同理,数据集B可分别整理为B1、B2和B3。数据集详细信息如表1所示。

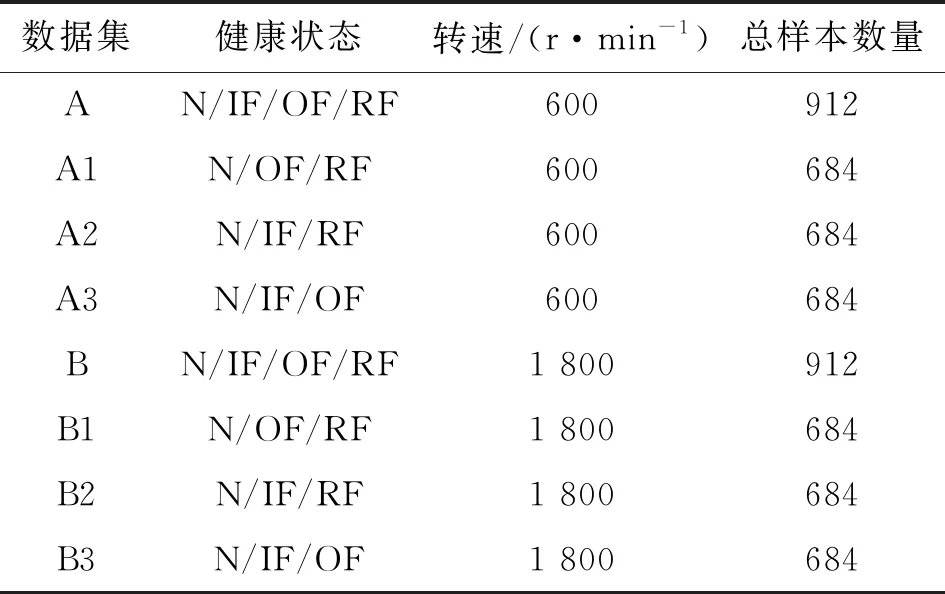
表1 不同工况下的齿轮箱轴承数据

在诊断实验中,分别以A1、A2和A3为源域数据集、B为目标域数据集,以B1、B2和B3为源域数据集、A为目标域数据集,共可设置6组开集诊断任务。为方便表示,使用A1→B表示数据集A1为源域、数据集B为目标域的诊断任务。在训练中,源域数据集的标签已知,目标域数据集的标签未知。使用全部源域数据与60%目标域数据作为训练数据,使用剩余40%目标域数据作为测试数据。齿轮箱轴承开集迁移诊断实验及数据使用比例如表2所示。

表2 齿轮箱轴承开集迁移诊断实验及数据使用比例

在诊断实验前,对影响提出方法诊断精度的主要因素开展研究工作,即:模型网络深度的确定,式(14)样本权重关系的准确性,阈值w0的选择。同时,为保障实验结果具有较好的鲁棒性,在每次诊断任务中,实验重复10次,计算平均诊断精度与精度波动方差作为最终结果。

提出方法使用卷积神经网络进行特征提取,其网络深度对开集迁移诊断具有影响,因此首先确定网络深度。卷积神经网络结构主要由卷积层、池化层与激活层重复叠加构成,在实验中将卷积层、池化层与激活层视为1层网络深度,则2～6层网络深度下的故障识别精度如图4所示。可以看出,当网络深度到达4后,提出方法诊断精度平稳且波动方差不大,但训练时间仍在增加。因此,在后续实验中将网络深度设置为4。

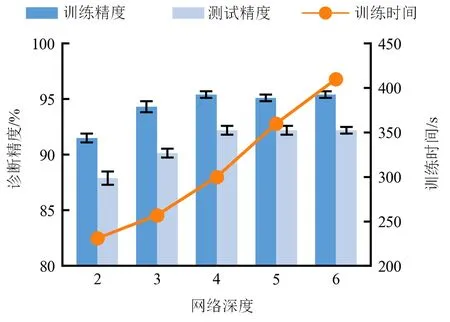
图4 不同网络深度的对比结果

式(14)样本权重关系的准确性是提出方法有效区分轴承目标域共享集与未知集的基础。将单次诊断任务的目标域测试样本权重绘制在图5中。可以看出,目标域共享集与未知集的样本权重在数值上具有明显差异,因而可以通过设置阈值,对轴承目标域共享集与未知集样本进行识别。

图5 目标域测试数据的样本权值

根据图5可知,目标域共享集与未知集样本的权值具有明显边界,其阈值可以设置为0。本文以表2中的6组实验任务为验证对象,获得不同阈值下轴承开集迁移诊断精度的平均值,如图6所示。可以看出,当阈值w0为0时,提出方法具有最高的诊断精度,且方差较小。因此,将0作为区分目标域共享集与未知集样本的阈值。

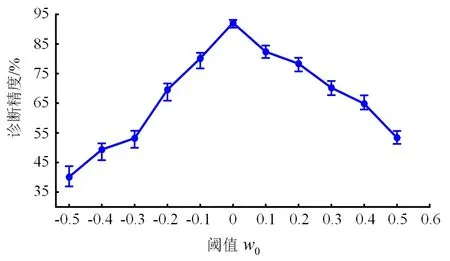
图6 不同阈值w0下提出方法的诊断精度

将提出方法用于表2中的6组迁移诊断任务,并与3种典型迁移诊断方法进行对比分析。3种方法分别为:DANN,Tzeng等[23]提出的对抗性领域自适应网络(adversarial discriminative domain adaptation,ADDA),Wang等[24]提出的迁移注意领域自适应网络(transferable attention for domain adaptation,TADA)。在诊断时,3种典型迁移诊断方法使用的特征提取网络与提出方法相同,以避免特征提取对结果的影响。此外,3种方法的超参数(学习率、训练批次、误差权衡参数等)均参考原文,以避免因参数设置不合理对诊断结果的影响。上述参数设置在其他诊断案例统一使用。

诊断结果如图7所示。可以看出,DANN对6组诊断任务的平均精度为70.84%,ADDA的平均精度为65.12%,TADA的平均精度为74.11%,提出的方法平均诊断精度为91.62%。因此,与传统迁移诊断方法相比,提出方法对滚动轴承开集数据的故障诊断具有显著优势。

图7 不同方法对变工况下齿轮箱轴承的诊断结果对比

以实验任务A1→B为例,展示不同方法的诊断结果混淆矩阵,如图8所示。可以看出:轴承开集数据的故障识别精度,主要在于能否有效剔除目标域中未知故障样本。经典迁移诊断方法DANN、ADDA与TADA可通过领域自适应方法识别目标域共享集故障样本,但在训练过程中直接对齐源域与目标域数据分布,没有针对未知故障样本采取额外措施,使得目标域未知故障样本被完全错分为其它健康状态,造成方法整体故障识别精度的降低。本文提出的方法首先利用样本权重度量领域相似性,剔除了71.8%的未知故障样本,再利用故障分类器实现目标域其他样本的故障识别,使得整体故障识别精度得到明显提升。

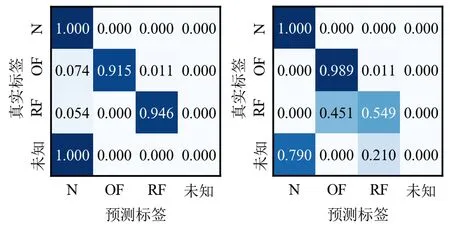
(a)DANN (b)ADDA

3.2 案例2:凯斯西储大学轴承数据验证

使用凯斯西储大学滚动轴承数据集[25]对提出方法进行验证。该数据集包括轴承正常、内圈故障、外圈故障和滚动体故障的样本,每种健康状态样本分别在0、0.75、1.49、2.24 kW共4种工况下进行采集。因此,该数据集涵盖了不同工况、不同健康状态下滚动轴承的监测数据,故障信息全面,很适合利用该数据集设计开集迁移诊断实验,验证提出方法的有效性。同时,由于数据公开使用,也方便其他学者对比诊断结果。

本文依次将上述4种不同工况下的轴承数据集分别定义为数据集D、E、F、G,每个数据集包含轴承正常状态的300个样本、每种故障状态的200个样本,每个样本长度为1 044。针对轴承开集诊断实验,依次剔除数据集D中内圈故障、外圈故障和滚动体故障,并定义为D1、D2和D3。实验中,以数据集D1、D2和D3为源域,以数据集E、F和G作为目标域,进行9组迁移诊断实验,模拟空载工况数据向其他工况数据的迁移诊断。实验设置、参数选择均与案例1相同。

不同方法的诊断结果如图9所示。可以看出:提出方法的平均诊断精度为90.57%,而其他3种方法诊断精度均未超过80%。其主要原因在于提出方法设计了加权领域鉴别器,剔除了未知故障样本对迁移诊断的影响,进而提高了诊断精度。

图9 凯斯西储大学轴承数据的迁移诊断结果

3.3 案例3:机车轮对轴承开集迁移诊断

针对某型电力机车的轴承状态监测,搭建测试台架,并使用液压系统来驱动和加载,模拟实际工况。该机车使用轴承型号为552732QT,其监测数据在两种转速波动区间下采集,采样频率为12.8 kHz,低转速区间约为490～530 r·min-1,高转速区间约为600～650 r·min-1。每种转速区间分别采集轴承正常、内圈故障、外圈故障与滚动体故障的加速度信号,故障照片如图10所示。

(a)轴承外圈故障 (b)轴承内圈故障 (c)轴承滚动故障

将两种转速区间下的轴承数据分别记为数据集H与L,每种健康状态有200个样本,每个样本包含1 044个数据点。针对轴承开集诊断实验:依次剔除数据集H中内圈故障、外圈故障和滚动体故障的样本,并分别定义为H1、H2和H3;同理,数据集L可分别整理为L1、L2和L3。不同迁移诊断任务的故障识别结果图11所示。可以看出:提出方法在机车轮对轴承开集迁移诊断中平均精度为89.77%,高于其他传统迁移诊断方法,与本文其他两个开集诊断案例的结论相同。

图11 机车轮对轴承的迁移诊断结果

4 结 论

针对滚动轴承目标域额外故障样本影响其故障诊断精度的问题,提出了采用深度迁移学习与自适应加权的轴承故障诊断方法,结论如下。

(1)加权领域鉴别器通过对轴承样本自适应赋予权重,控制样本的领域相似性程度,再利用权重阈值,区分源域和目标域中共享集与未知集样本,降低了未知集样本对轴承迁移诊断的影响。

(2)利用齿轮箱轴承、凯斯西储大学轴承、机车轮对轴承的3个故障诊断案例,验证了提出方法的有效性,相比传统迁移诊断方法,提升了开集数据下滚动轴承的故障识别精度。

(3)通过图8(d)可以看出,提出方法识别未知故障样本的精度为71.8%,究其原因是采集轴承样本时,受背景噪声等随机因素影响,部分样本的故障信息被淹没,导致部分未知集样本与轴承目标域共享集样本分布差异性减弱,降低了未知故障样本的识别精度。因此,如何克服随机因素影响、更加有效地计算未知样本权重是后续的重点研究内容。