量子遗传算法对砂类边坡稳定性敏感度的分析

王海龙，刘丽峰

(山东理工大学 建筑工程学院,山东 淄博 255049)

边坡稳定性问题是岩土工程界长久以来的经典技术问题，迫切需要寻找和开发出分析与应对方案[1]。杨俊[2]提出了一种基于多种群遗传算法的边坡研究方法，将遗传算法应用到边坡稳定性问题的分析上，构建了一个广泛且多功能通用的稳定性分析模型；胡培强等[3]利用强度系数折减有限元法，对边坡的多种参数建立影响因子方程，得出边坡稳定性不同影响因素的数值对比，其使用软件进行分析，结果具有可靠性和便捷性。王娅娟[4]利用Matlab软件以转角为搜索依据对边坡进行破裂面搜索，编写了可靠性与敏感度分析程序，程序开源可复刻性高。

由于传统的遗传算法收敛速度较慢，且容易陷入局部最优解，对于边坡稳定性一类拥有多元变量的解算，需要极力避免局部最优情况。针对这类问题，在传统遗传算法中引入量子比特与量子旋转门的概念，使种群编码与进化策略上与遗传算法有所不同，通过量子位同时表达多个染色体状态信息，再通过量子旋转门对量子比特的相位进行变换，实现其概率幅更新，以达到基因变异的效果，增加其进化的复杂度，使易陷入局部最优解的情况得以改善。

1 边坡参数的敏感度计算

1.1 影响程度的数学表达

边坡稳定系数主要与边坡高度h、坡度/坡角β、土体容重γ、土体黏聚力c、土体内摩擦角φ等参数有关，分析参数对边坡稳定性的影响程度可构建敏感度方程如下：

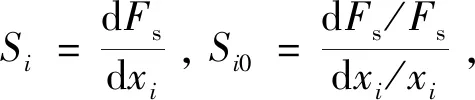
(1)

式中：Si是参数影响系数；Si0为无因次影响因子；Fs为边坡稳定系数；xi为任意参数。

1.2 边坡稳定性分析

设坡高为h，任一破裂角为α，坡角为β，土体重度为γ，L为破裂面边长，可表示为L=W/sina。边坡滑动体截面ΔABC重力可记作W，W=SΔABC×γ，滑坡体受重力分力，从而产生沿破裂斜面下滑的力F下，而坡体内部的内摩擦力等内应力则产生一个与下滑力方向相反沿斜面向上的妨碍下滑的摩擦力，记为抗滑力F抗，F下与F抗在物理关系上可作如下表示：

F下=Wsinα,F抗=Wcosα×tanφ+c×L，

(2)

此时Fs即可表示为

(3)

式中c为土体黏聚力。

以此为基础，可以将边坡最危险滑动面检索问题设计为多元函数寻优问题，而边坡最危险滑动面即为函数寻优的结果。根据参数模拟变化，可进一步推算该边坡在不同条件下的破裂角与稳定性。

2 研究方法

2.1 量子比特编码

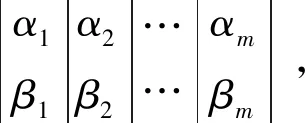
染色体的编码方式通过量子位概率幅进行表达：

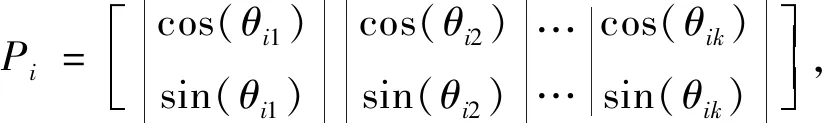
(4)

θij=2π×rand,i=1,2,…,n,j=1,2…，k，

(5)

式中：θ为量子比特的相位；N为染色体数量；k为量子位的位数；rand为[0,1]范围内的随机数。

2.2 量子旋转门

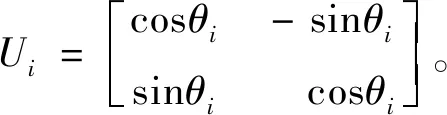
3 算例分析

3.1 边坡稳定性对边坡参数的敏感度实例分析

根据公式(3)，可以将边坡稳定性问题简化为一个以破裂面和稳定系数为基准的多元函数寻优问题，并以边坡极限平衡条件下的稳定系数方程建立边坡的数学模型。通过QGA进行寻优，可以得出在不同破裂面的稳定系数以及同一破裂面在不同参数波动的条件下的稳定系数变化。

如图1、图2所示，坡高和土体容重对边坡稳定性具有负相关作用，但边坡稳定性对土体容重的敏感度较低。坡度与坡高的增加都会直接导致任一破裂体的破裂角增大，下滑力显著提升。容重的上升则会导致破裂体下滑力的增加，使边坡稳定性降低。

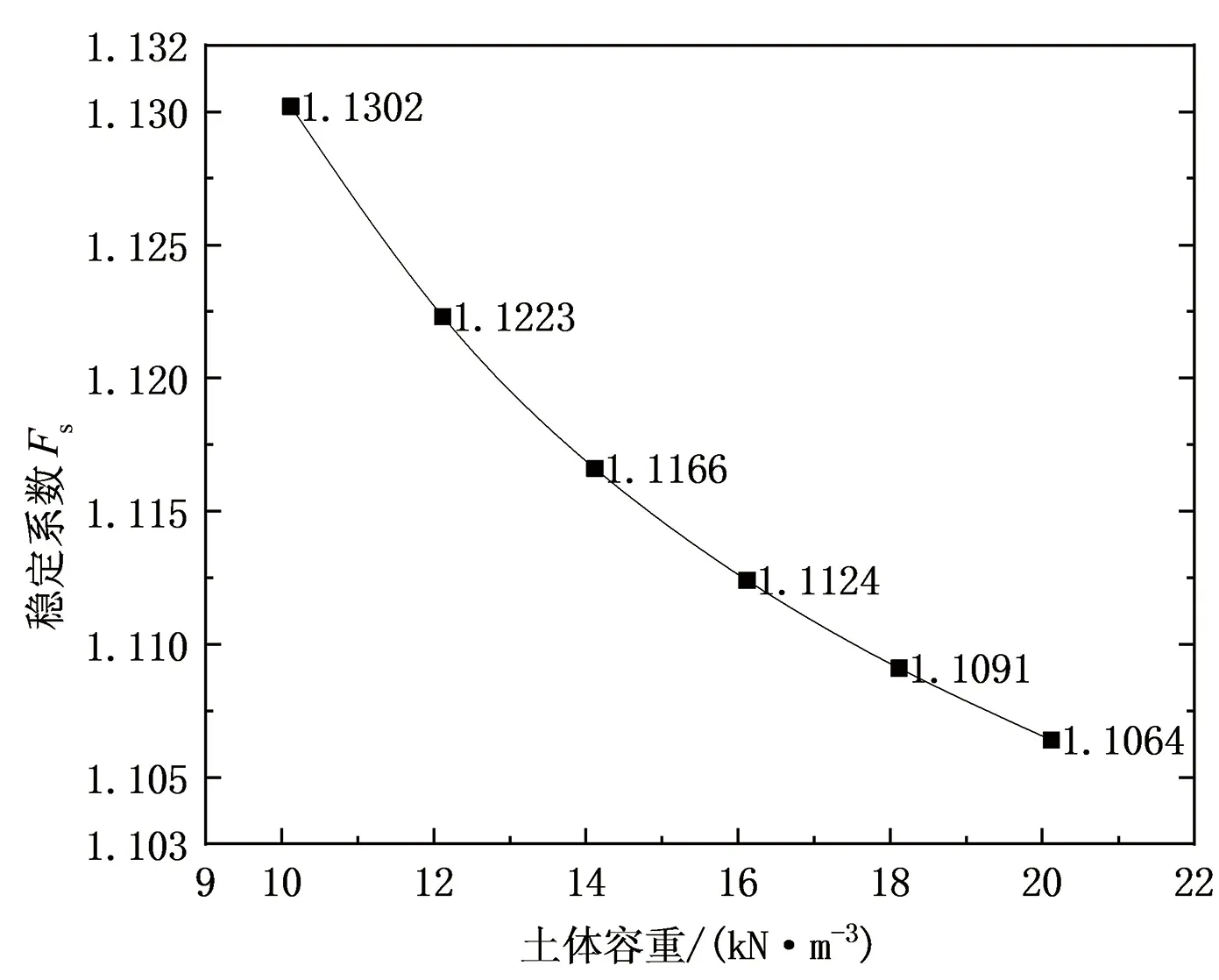
图1 土体容重对边坡稳定性影响程度曲线Fig.1 Curve of influence degree of soil bulk density on slope stability

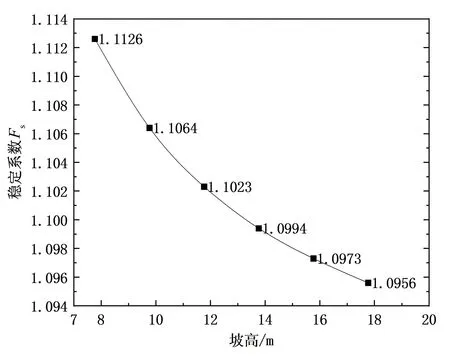
图2 边坡高度对边坡稳定性影响程度曲线Fig.2 Curve of influence degree of slope height on slope stability

通过单个边坡与单个数据的约束变异无法完全显示各参数变化时对边坡稳定性的影响程度，因此，还要让边坡对不同参数改变之间产生的敏感度进行对比分析，以得出进一步的结论。

黏聚力和内摩擦角增大均会引起边坡稳定性的增加，反之二者减少也会削弱边坡的稳定性。那么在同等变化条件下，约束内摩擦角的黏聚力变化导致稳定系数变化量为Δc，约束黏聚力的内摩擦角变化导致稳定系数的变化量为Δφ，对比二者的敏感度，同时不断改变边坡坡度，可以得出不同坡度条件下的敏感度。通过计算，坡角为26.56°的条件下边坡稳定系数对二者的敏感度如图3、图4所示。

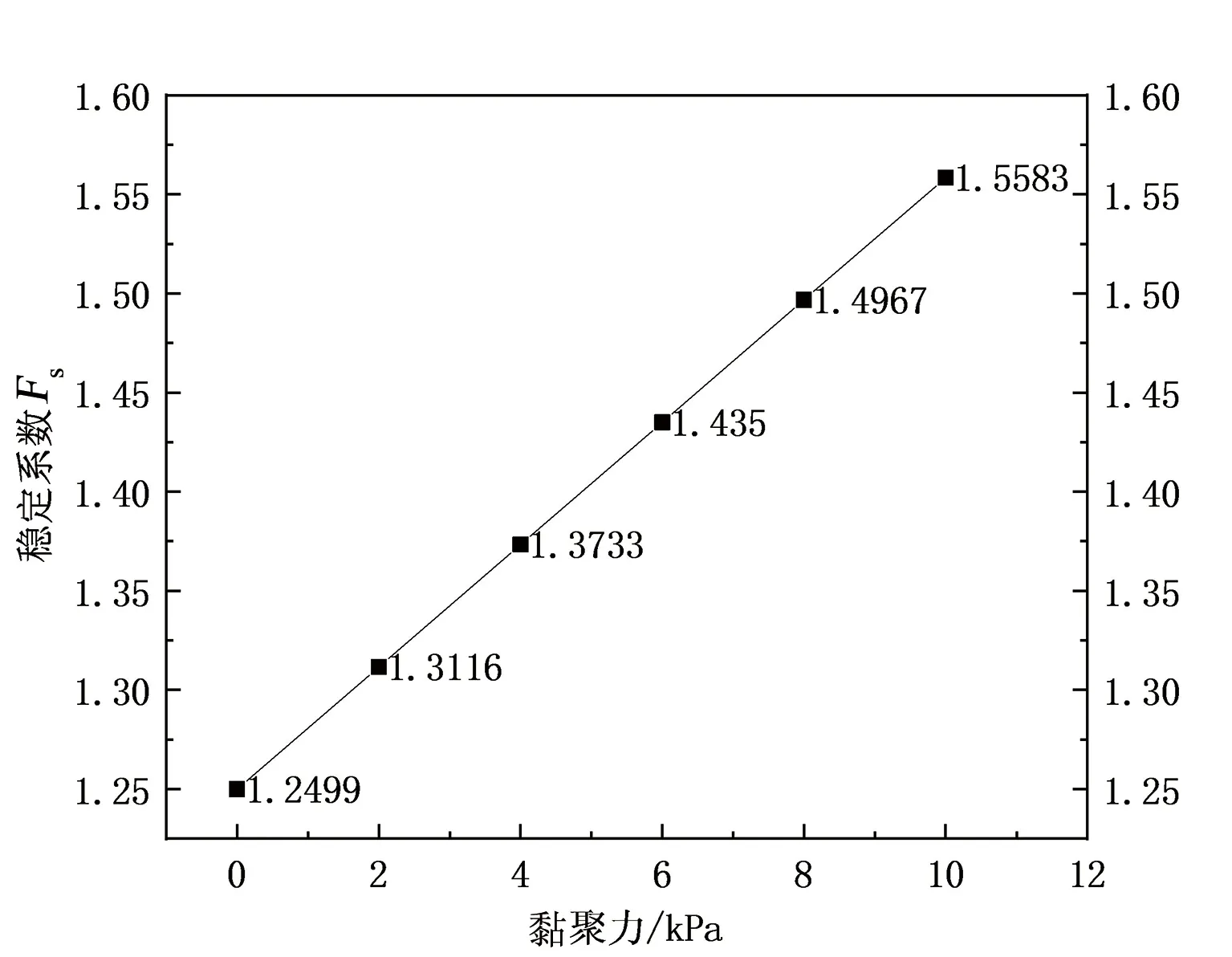
图3 土体黏聚力对边坡稳定性影响程度曲线Fig.3 Curve of influence degree of soil cohesion on slope stability

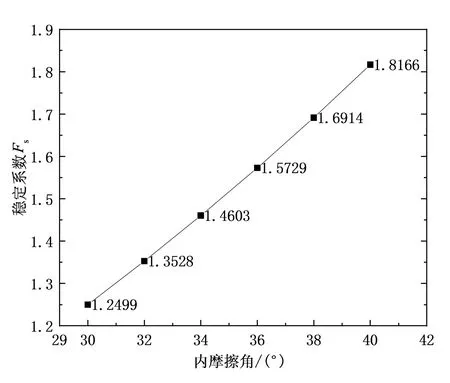
图4 土体内摩擦角对边坡稳定性影响程度曲线Fig.4 Curve of influence degree of internal friction angle on slope stability

黏聚力与内摩擦角对边坡稳定性均具有正相关关系，在此算例同等变异量下，内摩擦角变化时对稳定系数的影响小于土体黏聚力对边坡稳定性的影响。

3.2 不同容重条件下黏聚力的敏感度发生变化

土体容重的改变，不仅会影响稳定系数，还会影响参数的敏感度。土体容重增加会导致土体抗剪强度增加，提升土体稳定性，也会让黏聚力对稳定系数的影响程度增加。当容重降低时，虽然在相同条件下稳定系数的改变并不剧烈，但稳定系数对内摩擦角和黏聚力的敏感度发生了变化，影响程度变化如图5、图6、表1所示。

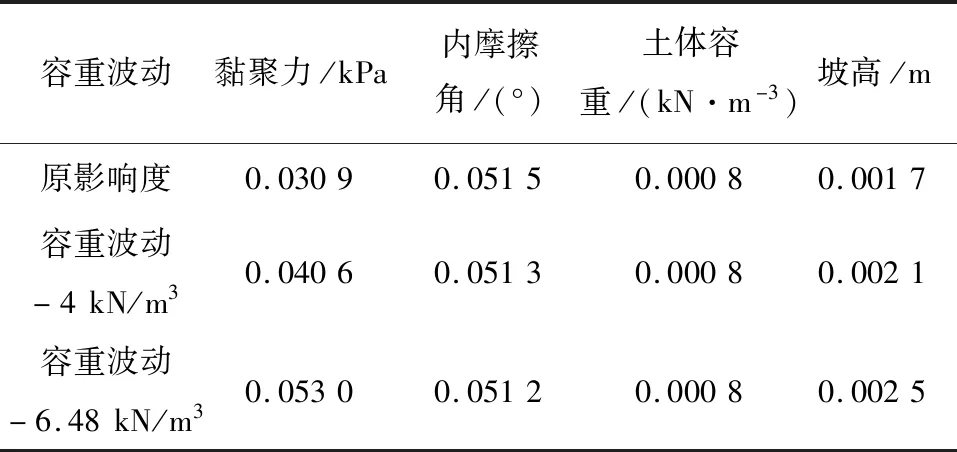
表1 影响程度分析Tab.1 Impact degree analysis

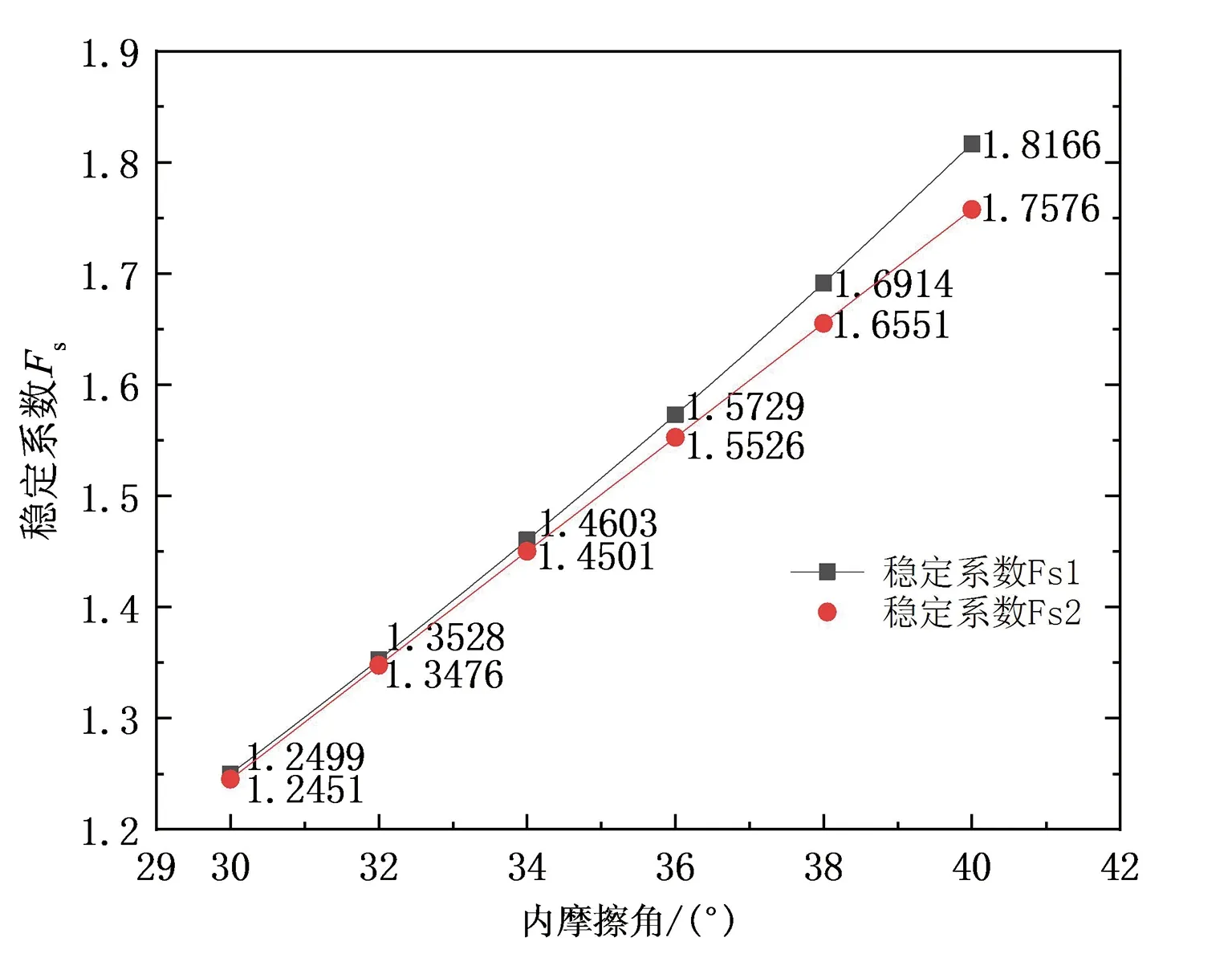
图5 容重波动后的内摩擦角敏感度变化曲线Fig.5 Sensitivity curve of internal friction angle after bulk density fluctuation

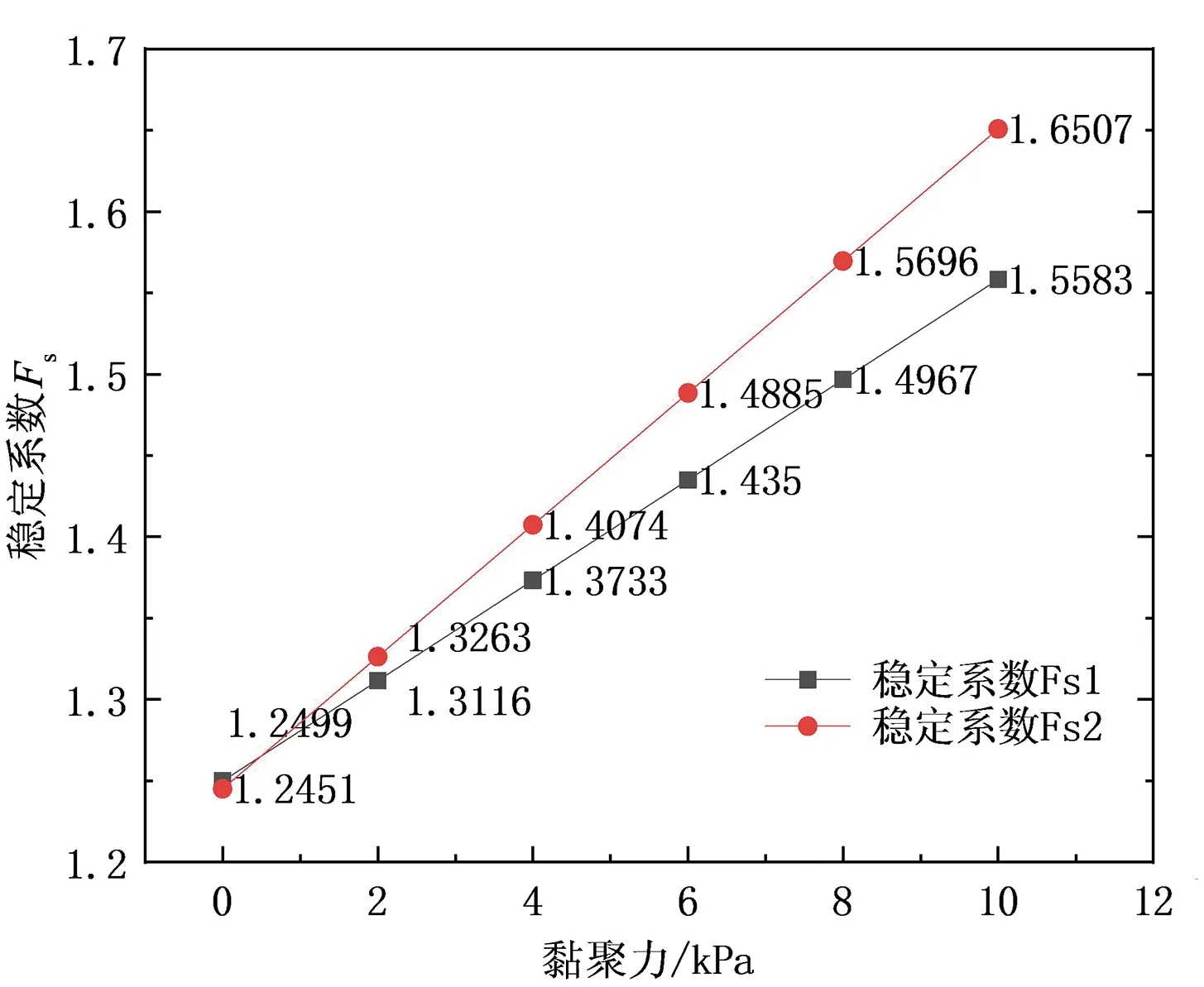
图6 容重波动后的黏聚力敏感度变化曲线Fig.6 Cohesion sensitivity curve after bulk density fluctuation

容重降低了4 kN/m3时，同等变异程度下，内摩擦角对稳定系数的影响度由0.051 5降低至0.051 3，

呈现微弱正相关变化。黏聚力对稳定系数的影响度由0.030 9增至0.040 6，在土体容重发生变化时，黏聚力对边坡稳定性的影响度呈现负相关变化。

土体容重的降低会导致土体抗剪强度降低与坡体滑动力的上升。假设边坡破裂体下滑力函数F(x)=f(γ)·f(φ)+f(c)，其中：f(γ)为破裂体的质量，是土体容重γ与土体体积的乘积；f(φ)为土体内摩擦角φ的正切；f(c)为土体黏聚力c与破裂体斜边长度的积。边坡任一破裂体的容重降低即f(γ)·f(φ)降低时，会导致内摩擦角对稳定系数影响程度的降低，即内摩擦角对边坡稳定性的影响程度与土体容重呈正相关关系。土体黏聚力对稳定性的影响则表示为对破裂体质量函数的和，即当土体容重降低时，内摩擦角的影响程度占比减小，使黏聚力对稳定系数的影响程度占比增大，即黏聚力对边坡稳定性的影响程度与土体容重呈负相关关系。

经过计算，在坡高h=9.77 m，坡角β=24.45°，土体容重γ=10.22 kN/m3，内摩擦角φ=20.84°时，黏聚力对边坡稳定系数的影响度增至0.052 97，此时黏聚力对稳定系数的影响度超过内摩擦角，边坡参数的主导影响因素由内摩擦角转变为黏聚力。在实际环境中，降水、路面压力、地下水位、坡体高度等因素变化时，土体容重并非一成不变，也会导致此类情况的发生。

3.3 与软件模拟结果对比

文献[3]提出了一种基于强度系数折减法与迈达斯GTS软件的边坡系数敏感度的分析方法，构筑了敏感度曲线模拟函数，并提供了实例计算数据。通过与现有软件及其实例的对比，可观察出通过QGA数值模拟进行计算参数敏感度结果的可靠性。在相同实例下，计算的参数平均敏感度得出的结果对比见表2。

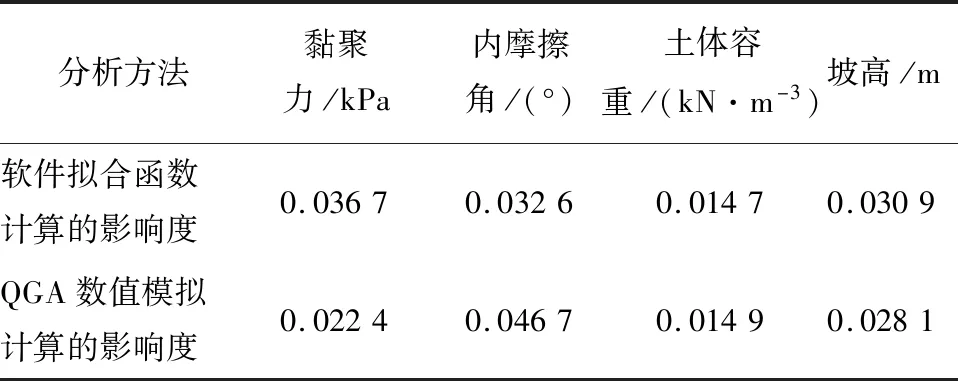
表2 不同分析方法的结果对比Tab.2 Results comparison of different analytical methods

文献[3]中提供的坡高波动区间为8 m至14 m。如图7所示，在这个区间内，QGA数值模拟与边坡分析软件的拟合函数的结果大致相同，最大差异度小于2%,但根据函数拟合额外增加波动区间、即边坡高度范围在小于8 m以及大于14 m后，软件函数模拟出现了奇异值。根据边坡稳定性理论，边坡高度上升会导致边坡失稳，因此在超出原波动范围时，软件函数模拟的结果会出现较大误差；而在软件拟合较为正确的区间内，QGA数值模拟与软件模拟的结果大致接近。

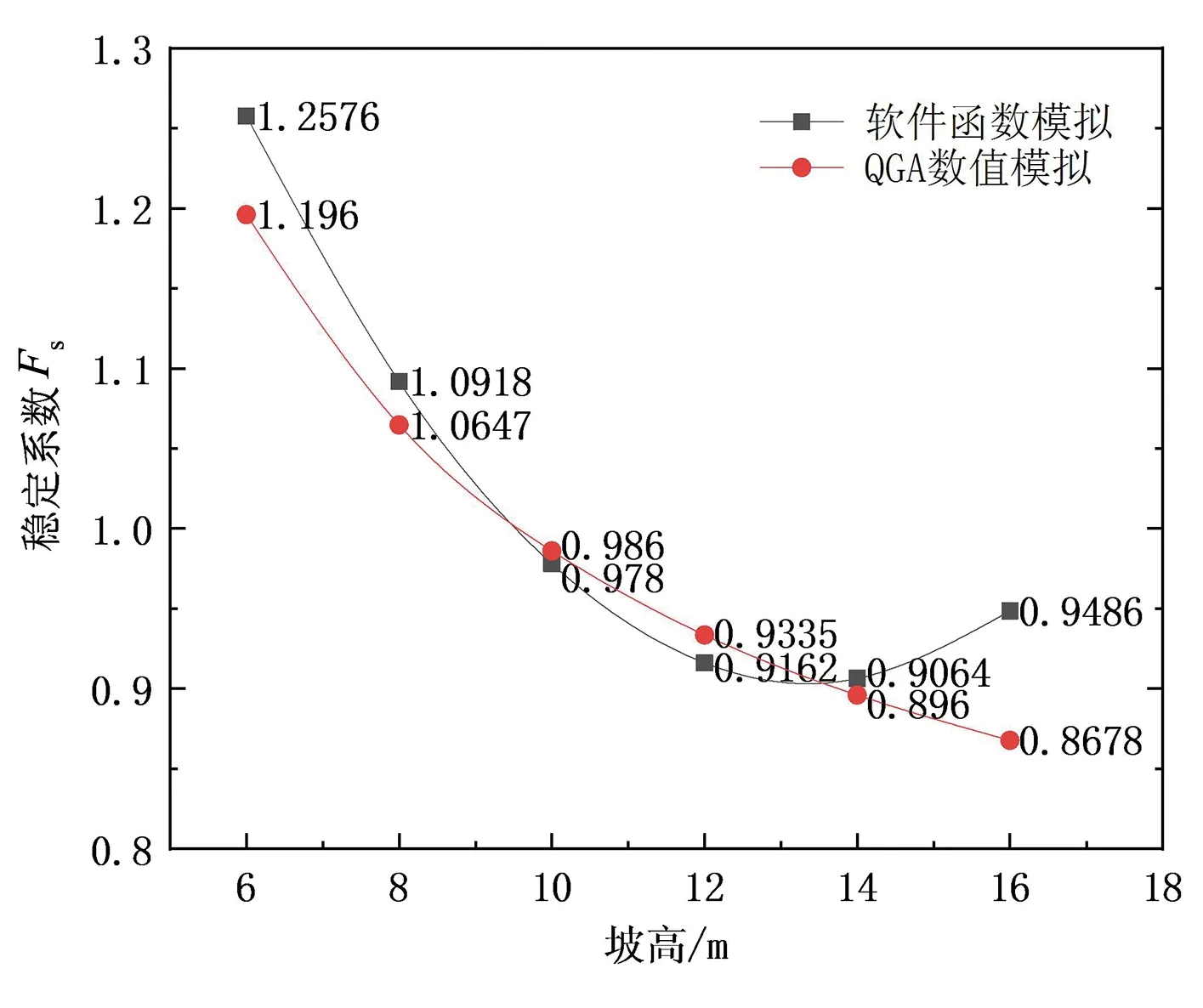
图7 边坡高度对边坡稳定性的影响关系曲线Fig.7 Influence curve of slope height on slope stability

如图8所示，在分析黏聚力时，QGA出现了差异值。原因可能是：由于土体黏聚力对边坡土体的其他因素变化响应较大，而本程序在借用文献[3]算例时，由于土壤性质、函数模型、其他土体参数、搜索方式等的差异，导致了QGA计算的土体黏聚力对边坡稳定性的敏感度发生下降，实际影响度从0.036 7降低至0.022 4。

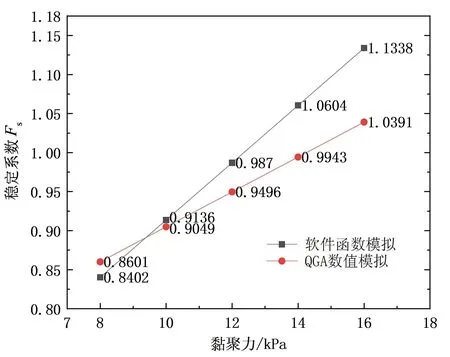
图8 土体黏聚力对边坡稳定性的影响关系曲线Fig.8 Influence curve of soil cohesion on slope stability

如图9、图10所示，在软件指定的参数变化区间内，QGA数值模拟和软件的拟合函数得出的结果具有相似性。

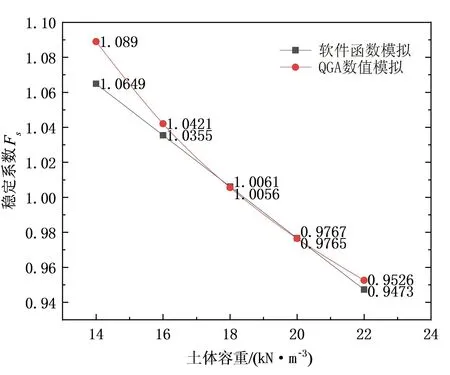
图9 土体容重对边坡稳定性的影响关系曲线Fig.9 Influence curve of soil bulk density on slope stability

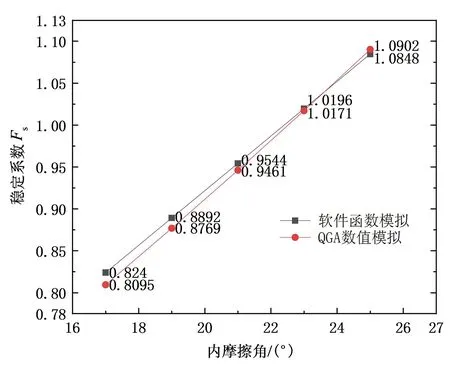
图10 土体内摩擦角对边坡稳定性的影响关系曲线Fig.10 Influence curve of soil internal friction angle on slope stability

4 结论

通过量子遗传算法将边坡问题进行数值模拟，将影响边坡稳定性的不同参数之间的敏感度进行分析，并对比了部分参数的敏感度，分析了不同参数在边坡稳定性上的影响方式，得出以下结论：(1)边坡稳定系数对土体容重的敏感度较低，但会通过影响其他参数的敏感度进而影响边坡整体;(2)同等参数条件下，内摩擦角、黏聚力、土体容重对边坡的影响程度较为均匀，基本呈现线性趋势，具有一定的可预测性;(3)土体黏聚力和内摩擦角的波动几乎不会影响彼此的敏感度;(4)土体容重的降低会使黏聚力敏感度有较大程度的增加。可以推论，在容重低于一定值时，对边坡稳定系数影响的主导因素会发生变化。

综上所述，对边坡稳定性带来的影响即敏感度而言，内摩擦角>黏聚力>土体容重，然而，土体容重尽管对稳定系数的影响相对较小，却会较大程度地改变边坡稳定性对黏聚力的敏感度。这一点具有现实意义，随着土层深度的增加，在重力作用下容重也会发生改变，随之改变边坡稳定系数对不同参数的敏感度。针对不同层土体，对边坡治理过程中要注意分析影响稳定性的主导因素，针对性治理。