基于区间二元语言毕达哥拉斯主成分分析的TODIM方法及其应用

张拴娥

(西安建筑科技大学 理学院，陕西 西安 710055)

毕达哥拉斯模糊集已被广泛应用在解决多属性问题中。Garg[1]研究了犹豫毕达哥拉斯模糊信息的Maclaurin对称平均算子及其应用，Rong等[2]研究了语言毕达哥拉斯模糊信息的Einstein算子及其应用，Deng等[3]研究了二元语言毕达哥拉斯模糊信息的Heronian算子及其应用，Liang等[4]研究了区间毕达哥拉斯模糊信息的Bonferroni算子及其应用。由于实际问题的复杂性和不确定性,已提出的毕达哥拉斯模糊集不能准确地表达评价信息。区间二元语言能够有效避免语言评价信息在集结过程中出现信息损失的问题，提高了语言信息集结结果的精确性。将语言集与毕达哥拉斯模糊集相结合，提出的区间二元语言毕达哥拉斯模糊集不仅可以全面地表达决策信息，而且能更好地反映问题的特点。为满足决策的需要，本文的评价信息以区间二元语言毕达哥拉斯模糊数的形式给出。

目前已有的多属性决策相关方法大多是建立在决策者完全理性的基础上。但在现实中，往往由于问题本身具有的不确定性以及决策者认知的局限性，无法达到完全理性。由此，Gomes等[5]以前景理论为依据，提出了交互式多准则决策方法(TODIM)，该方法一经提出，便受到了学者的关注。Ding等[6]研究了基于区间犹豫模糊环境的TODIM方法，Zhang等[7]研究了基于二元语言毕达哥拉斯环境的TODIM方法，张燕等[8]研究了基于犹豫毕达哥拉斯环境的TODIM方法，Huang等[9]研究了基于区间语言毕达哥拉斯环境的TODIM方法。因为在复杂环境下时间和计算复杂度的提高不利于TODIM实现，所以需要对TODIM方法进行优化。主成分分析模型(PCA) 能够在较大限度保留原始数据信息的基础上，对高维变量进行集成和简化，能够更集中、更典型地反映研究对象的特征，在工程管理、风险投资、城市综合实力评价等众多领域得到广泛研究和推广。Liu等[10]研究了基于直觉模糊主成分分析模型的复杂多属性群决策方法，黄利文[11]研究了基于理想点的主成分分析法在综合评价中的应用，Xian等[12]研究了基于主成分分析模型在地震应急方案中的应用。

目前基于区间二元语言毕达哥拉斯模糊主成分分析的TODIM多属性决策问题鲜有研究，本文为了能够获得更加合理的属性和决策者的权重，并消除多个变量之间的相关性，构造区间二元语言毕达哥拉斯模糊主成分分析模型(I2PFLV-PCA)；提出基于区间二元语言毕达哥拉斯主成分分析的TODIM方法解决复杂的多属性问题；将此方法与传统的TODIM方法以及Wei等[13]提出的聚合算子方法进行比较分析。

1 预备知识

定义1[14]称二元组(si,αi)为二元语言评价值，其中,si表示集合S的第i个语言变量，αi∈[-0.5,0.5)为符号转移变量，用来表示与评价信息si的偏差。

定义2[13]设评价信息λ为实数，可通过函数Δ将λ转换为二元语言信息：

其中round(λ)表示四舍五入取整算子。存在逆映射Δ-1，使得Δ-1(si,αi)=i+αi=λ。

定义3[15]设有二元语言(si,αi)和(sj,βj)，si,sj∈S,αi,βj∈[-0.5,0.5)且(si,αi)≤(sj,βj)，则称[(si,αi),(sj,βj)]为区间二元语言。运用函数Δ可以获得与区间数Δ[λ1,λ2]，λ1,λ2∈[0,1],λ1≤λ2对应的区间二元语言：Δ([λ1,λ2])=[(si,αi),(sj,βj)],其中，i=round(λ1),j=round(λ2),α=λ1-i,β=λ2-j。同样存在函数Δ-1,将二元语言变量转化成[λ1,λ2]，Δ-1[(si,αi),(sj,βj)=[λ1,λ2]。

2 区间二元语言毕达哥拉斯模糊集

[μL(x),μU(x)],[νL(x),νU(x)]|x∈X>。

其中:0≤(μU(x))2+(νU(x))2≤1;α(x),β(x)∈[-0.5,0.5)。

定义5设X是论域，S是有限语言集，区间二元语言毕达哥拉斯模糊集

]|xi∈X>(i=1,2)的运算律：

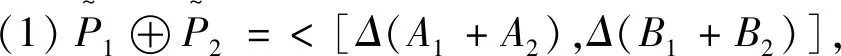
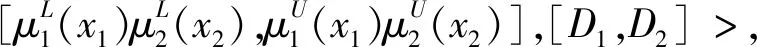
其中:

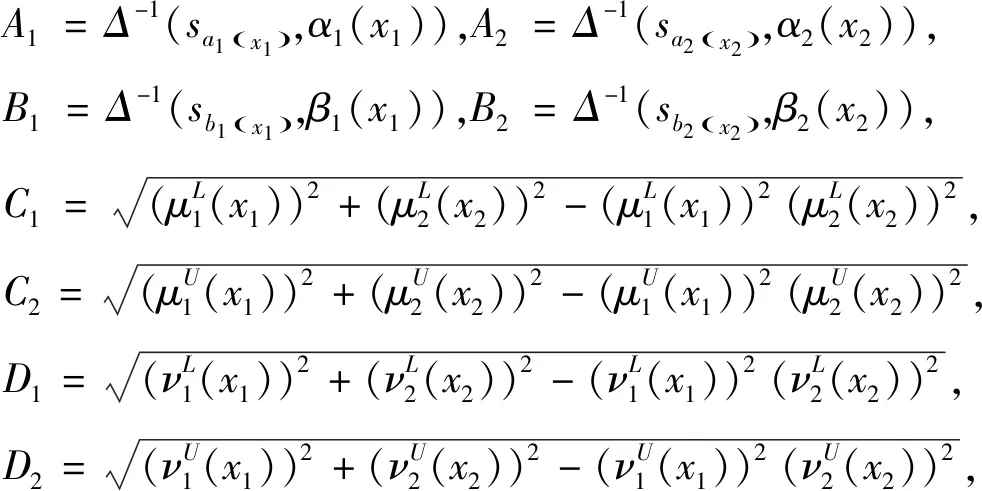
定义6设X是论域,S是有限语言集，

(1)

式中：l为语言变量的值；A1=Δ-1(sa1(x1),α1(x1))；A2=Δ-1(sa2(x2),α2(x2))；B1=Δ-1(sb1(x1),β1(x1))；B2=Δ-1(sb2(x2),β2(x2))；

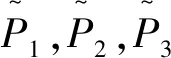
证明性质(1)证明：

性质(3)证明：

|Q1B1-P1B2+P1B2-P1B3|+

|Q2A1-P2A2+P2A2-P3A3|+

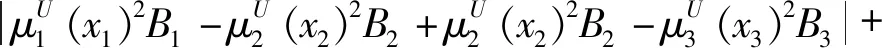
|Q2B1-P2B2+P2B2-P3B3|)≤

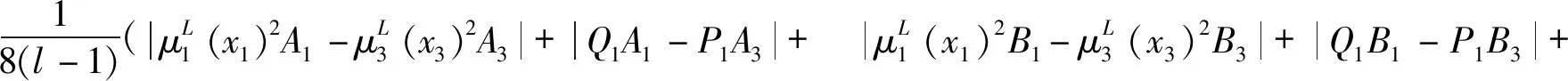
定义7设X是论域，S是有限语言集,

(i=1,2,…,n)是区间二元语言毕达哥拉斯模糊集，区间二元语言毕达哥拉斯模糊加权平均算子(I2PFLWAζ)和加权几何算子(I2PFLWGζ)是

的映射，分别表示为：

(2)

(3)

3 区间二元语言毕达哥拉斯模糊变量的统计特征

给出变量的均值、差值、方差以及协方差的定义及其计算公式。

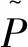
(4)

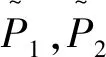
(5)

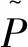
(6)

(7)

4 区间二元语言毕达哥拉斯模糊数的标准化

设

1)语言变量的标准化

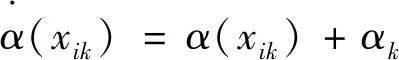
2)区间隶属度非隶属度的标准化

对于矩阵Y第k列，令γk=min{μL(xik),νL(xik)}，通过公式

γk,νU(xik)-γk]转化得到新的变量。然后

通过公式计算

得到新的隶属度非隶属度。

5 I2PFLV-PCA TODIM方法的应用

5.1 I2PFLV-PCA TODIM方法的决策步骤

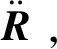
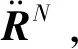
(8)

式中：

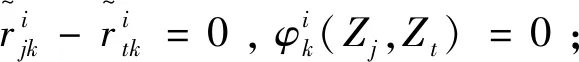
(9)

Zj(j=1,2,…,m)的累积优势度表示为

步骤6计算累积优势度矩阵。

(10)

总优势度φ(Zi)(i=1,2,…,m)为

(11)

步骤7计算总值Γ(Zi)(i=1,2,…,m)。

(12)

总值最大的方案是最理想的方案。

5.2 案例分析

到目前为止，预测火灾发生的时间和地点过于困难，因此火灾应急计划的选择是非常迫切和必要的，这有助于减少损失。本文将I2PFLV-PCA模型TODIM方法应用于紧急决策。

火灾应急决策有四种备选方案。四个决策者Di(i=1,2,3，4),用语言集S={si|i∈[0,8]}对四个初步设计方案Zj(j=1,2,3,4)进行评价，以确保决策的科学性。在评价阶段，每个方案考虑六种属性，这些属性包括：C1准备能力，C2救援能力，C3恢复能力，C4组织能力，C5响应时间，C6经济效率。

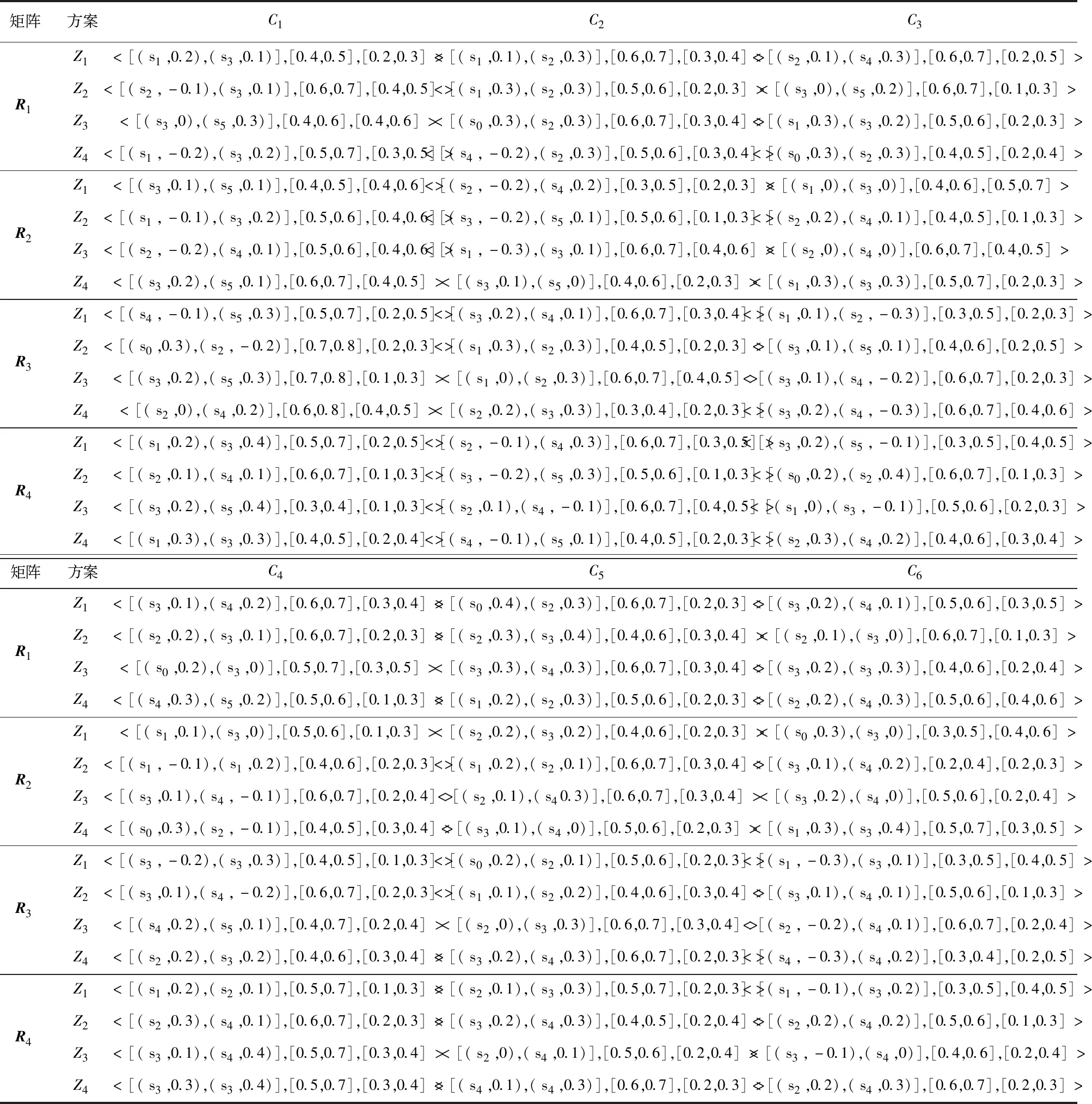
表1 决策矩阵Ri(i=1,2,3,4)Tab. 1 Decision matrix Ri(i=1,2,3,4)

根据公式(7)得到属性的样本协方差矩阵，见表2。基于协方差矩阵，求属性主成分的样本特征值、特征向量和贡献率，见表3。由表3可知前三个主成分的累积贡献率大于85%，充分表达了原始属性中包含的大部分信息。

表2 属性协方差矩阵Tab.2 Attribute′s covariance matrix

表3 属性主成分的样本特征值、特征向量和贡献率Tab.3 Eigenvalues,eigenvectors,and CCRs of attribute PCs

(s0.422,0.072)],[0.046 6,0.053 3],[0.232,0.268 5]>。

根据公式(7)得到决策者的样本协方差矩阵，见表4。基于协方差矩阵，求出决策者主成分的样本特征值、特征向量和贡献率，见表5。由表5可知前2个主成分的累积贡献率大于85%，充分表达了原始决策者中包含的大部分信息。

表4 决策者的协方差矩阵Tab.4 Decision maker′s covariance matrix

表5 决策者主成分的样本特征值、特征向量和贡献率Tab.5 Eigenvalues,eigenvectors,and CCRs of decision maker PCs

(s1.570 1,0.143 9)],[0.302 4,0.320 2],[0.849 4,0.947 3]>。

M1=

M2=

累积优势矩阵

步骤6根据公式(11)计算总优势度φ(Zi)。

(φ(Z1),φ(Z2),φ(Z3),φ(Z4))T=AωD= (-1.778 3,-0.672 9,1.443 7,-1.725 5)T。

步骤7根据公式(12)计算备选方案Zi(i=1,2,3,4)的总体值Γ(Zi)(i=1,2,3,4)。

(Γ(Z1),Γ(Z2),Γ(Z3),Γ(Z4))T=

(0,0.343 1,1,0.016 4)T,

最终排序：Z3≻Z2≻Z4≻Z1。

5.3 对比分析

为了进一步说明本文所提出方法的有效性，将该方法与传统的TODIM方法，以及Wei等[13]提出的加权几何算子聚合方法进行比较。

利用最大离差法确定权重。计算得出属性权重ωC=(0.153 0,0.136 7,0.184 8,0.182 6,0.184 1,0.158 9)T和决策者权重ωD=(0.253 3,0.275 6,0.278 4,0.192 6)T。

首先根据传统的TODIM方法，计算得到总优势度φ(Zi)(i=1,2,3,4)：

计算备选方案Zi(i=1,2,3,4)的总体值Φ(Zi)(i=1,2,3,4)：

(Φ(Z1),Φ(Z2),Φ(Z3),Φ(Z4))T=

(0.381 5,0,1,0.902 7)T。

得到最终排序：Z3≻Z4≻Z1≻Z2。

然后应用Wei等[13]提出的聚合方法计算。由于篇幅限制，本文仅给出C1属性下各方案的聚合结果：

(s3,-0.164)],[0.470，0.611],[0.316,0.667]>,

[0.530,0.656],[0.347,0.483]>。根据得分函数计算每个方案得分值:

得到最终排序：Z3≻Z4≻Z1≻Z2。

对比分析可知，利用I2PFLV-PCA的TODIM方法，传统的TODIM方法以及Wei等[13]提出的聚合方法计算，得出最优方案均为Z3，验证了本文方法的有效性。Wei等[13]采用直接聚合的方法,没有考虑极值对最终结果的影响,可能会得到不合理的结论。而本文所提出的方法在运算过程中将语言评价值采用平均值,这使决策过程更加科学合理。将传统的TODIM方法和I2PFLV-PCA的TODIM方法进行对比可以得出，如果存在多重共线性，传统的TODIM方法可能会得出不同的排序结果。本文提出的I2PFLV-PCA的TODIM方法的优点：(1)I2PFLV-PCA模型不仅有效地对数据进行降维，消除变量之间的相关性，并且可以获得合理的权重，这对TODIM方法非常重要；(2)I2PFLV-PCA的TODIM方法考虑了决策者的心理行为，能够在决策中获得更加精确的排序结果。

6 结论

1)区间二元语言毕达哥拉斯模糊数能够更加准确地描述决策者的评价信息，所以本文的评价信息以区间二元语言毕达哥拉斯模糊数的形式给出。

2)为了克服多重共线性，降低变量间的相关性，本文提出了I2PFLV-PCA模型，可以获得客观的关于属性和决策者的权重。

3)将I2PFLV-PCA模型和传统的TODIM方法相结合，提出的基于I2PFLV-PCA的TODIM方法，不仅用来处理大量的区间二元毕达哥拉斯模糊数数据，并且成功地描述了决策者在决策过程中的心理行为。

4)通过将本文提出的方法与传统的TODIM方法，以及Wei等[13]提出的聚合方法进行对比分析，验证了基于I2PFLV-PCA的TODIM方法的有效性和实用性。本文所提出的方法为解决复杂多属性决策问题提供了一种思路。