一类退化尖点环附近Melnikov函数展开式

尚德生，王政

(山东理工大学 数学与统计学院,山东 淄博 255049)

在平面分支理论研究中，同宿和异宿分支的研究是奇闭轨分支研究中的一个非常复杂而又有意义的课题。当一个给定系统的奇闭轨同宿或者异宿于有限个非退化的双曲鞍点时，已经有很多相对比较完善的理论和应用结果[1-3]。但是当奇闭轨同宿或异宿于非双曲鞍点，或者更加复杂的退化奇点(如退化鞍点或者尖点)时的分支问题研究，却是一个非常复杂而有意义的挑战。对于奇点是幂零鞍点和幂零尖点的情形下的奇闭轨分支问题，学者都进行了比较系统的讨论，并给出了具体的同宿轨附近的Melnikov函数的展开式[2,4-5]，并对一些不同类型的相关微分系统作了讨论和应用[6-8]。但是对更进一步的退化奇点情形的同宿或异宿分支问题，至今还没有见到比较系统的研究。本文在文献[2,4]的启发下，对一类具有退化尖点的同宿轨附近的Melnikov函数的展开式进行探讨，并给出m=1情形下展开式前几项的系数。

考虑微分系统

(1)

式中：φ(x)是次数大于2m的解析函数；p(x,y),q(x,y) 为x,y的多项式。显然原点O(0,0) 是未扰动系统(即ε=0 时)的一个退化尖点，这里假设ε=0时,未扰系统具有连接尖点O(0,0)的同宿轨。

因为未扰系统是一个哈密尔顿系统，且系统的哈密尔顿函数为

(2)

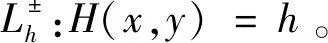
图1 未扰动系统(1)尖点环附近轨线分割图Fig.1 Orbit division near the cuspidal loop of the unperturbed system(1)

在周期区域Lh:H(x,y)=h,0<|h|≪1 内扰动系统(1)的极限环可由周期扰动下的一阶Melnikov函数M(h,δ) 的零点来确定。

下面讨论系统(1)的一阶Melnikov函数

(3)

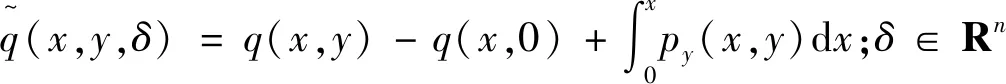
首先，当0<|h|≪1时，在原点附近存在唯一的解析函数x=θ(u) ，使得

(4)

成立。

若设

(5)

则将式(5)代入式(4)后，借助数学计算软件Mathimatica可根据需要递推求得前面各项的系数ej,j=2,3,… 。

(6)

式中：

∈Cω。

记

(7)

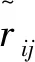
(8)

式中

(9)

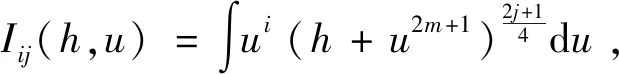
引理1对非负整数i=0,1,2,…,j=0,1,2,…，有Iij(h,u)满足如下递推公式:

(10)

(11)

因为对非负整数i,j存在唯一的k,l,r,s，使得i=(2m+1)k+r,j=2l+s，其中0≤r≤2m,0≤s≤1 成立。这样根据引理1的递推公式，容易得到引理2。

(12)

式中:

由于当i=2m时，有

(13)

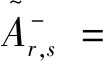
证明首先讨论当h<0 时的情形。对

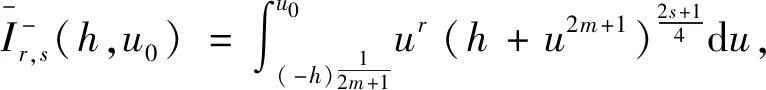
(14)

通过变量变换

(15)

可将式(14)化为

(16)

根据泰勒展开式

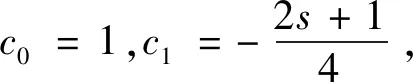
(17)

是与u0无关的收敛级数的和，而

|h|j∈Cω。

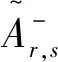
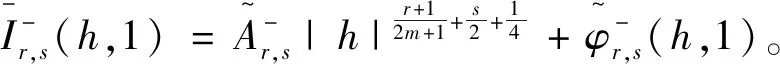
(18)

这样，一方面对式(18)关于h求偏导数，得

(19)

另一方面，由式(14)取u0=1，再关于h求偏导数，得

(20)

同样，经过变换(15)，可将式(20)化为

(21)

这样，当4r+2(2m+1)s<3(2m+1)-4 时，结合式(19)、式(21)得

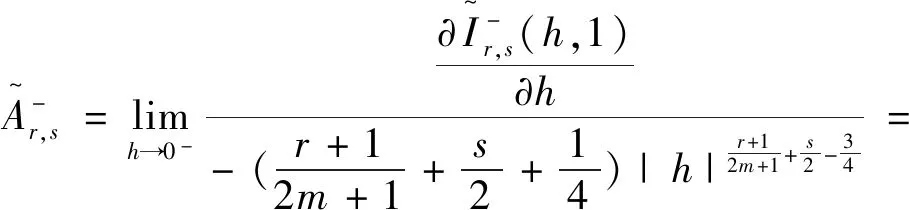
而当4r+2(2m+1)s>3(2m+1)-4时，由于

所以结合式(19)、式(21)，可以得到

下面再讨论当h>0 时的情形。利用

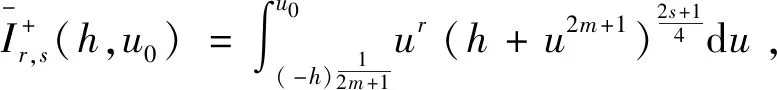
(22)

先经过变量变换

(23)

可将式(22)化为

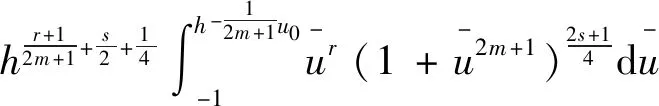
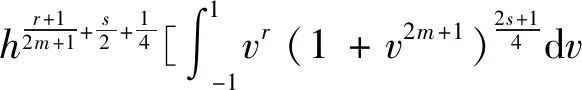
同样利用泰勒展开式

(24)

其中

是与u0无关的值，而

(25)

这样，一方面对式(25)关于h求偏导数，得

(26)

另一方面，对式(22)取u0=1，再关于h求偏导数，得

(27)

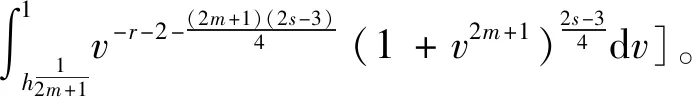
(28)

这样，当4r+2(2m+1)s<3(2m+1)-4 时，结合式(26)、式(28)可得

当4r+2(2m+1)s>3(2m+1)-4时，由于

所以结合式(26)、式(28)，可以得到

这样，根据式(8)，结合引理2及引理3可得

(29)

因此，利用式(6)、式(7)，并将式(29)代入式(6)，可以得到Melnikov函数在h=0 附近的一般展开式。

定理1在未扰系统具有式(1)形式的尖点环的假设下，尖点环附近的Melnikov函数展开式为

M±(h,δ)=

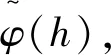
(30)

结合文献[2,4]的证明可知，若取m=1，则可得系统(1)展开到前八项的表达形式。

推论1在m=1时，系统(1)在尖点环Lh=0附近的Melnikov函数展开式为

并且展开式的系数为:

=0 ，