切削液影响BTA钻加工轨迹数值研究

刘晋丽，郑文源

(1. 西安航空职业技术学院，陕西 西安 710089；2. 西安华雷船舶实业有限公司，陕西 西安 710000)

0 引 言

深孔加工技术在装备制造业中应用广泛。随着技术的不断发展，对于深孔零件的要求也不断提升，但是由于深孔加工封闭与半封闭的特殊性，很难检测与控制其加工质量，故一直是一项瓶颈技术[1]。而钻杆在加工过程中出现的扰动现象会导致圆度形貌改变，产生凸角，在孔壁上生成不规则刀痕等，影响孔零件的使用，也大大降低了生产效率。因此，研究钻杆扰动的形成机理和抑制扰动的方法就显得极为紧迫。

切削液是深孔加工过程中不可缺少的物质，起着冷却、排屑等作用，但是其也对钻杆在加工过程中的运动产生了一定的扰动作用。本文以Timoshenko梁模型为基础，并考虑切削液因素，研究钻杆扰动形成的机理和轨迹模型。

1 BTA钻振动模型

1.1 Timoshenko梁模型

考虑到BTA钻杆的惯性和剪切变形的影响，其微分方程为[2]：

(1)

其中，E表示钻杆的弹性模量，G表示剪切模量，ρ表示钻杆材料密度，K表示钻杆的体型系数，I表示钻杆的转动惯量。假设式(1)解的形式为：

(2)

其中，ωi为BTA钻的固有频率，其表达式为：

(3)

从式(3)可以看出，剪切变形和转动惯量影响着钻杆的固有频率。

1.2 流固耦合振动模型

考虑到切削液引起的弯曲变形和惯性力，BTA钻系统的振动将是耦合振动，其微分方程为[3]：

(4)

其中，v表示切削液的流速，ρL为切削液的密度，m是钻杆和切削液组成的系统单元的单位质量，即将切削液及钻杆微观分解后组成的单位体积内的系统质量，则其解的形式为：

(5)

通过分析，由于切削液的变形和惯性力的影响，降低了钻杆的固有频率。

2 BTA钻削力分析

2.1 动态切削力的线性方程

当BTA钻在加工过程中受到理想位置的运动和速度影响时[4]，切削液对钻杆运动的作用也会发生改变，作用力与扰动的关系一般是非线性的，但是当干扰足够小时，周期关系可以表现为线性：

(6)

其中，Δ为位移变化量。式(6)的前提是扰动足够小，切削力与钻杆之间的作用力与钻杆的运动速度成正比，其表达式如下：

ΔFx=Fx-Fx0=kxxΔx+kxyΔy+

(7)

其中，kij表示刚度系数，cij表示阻尼系数，对应于式(6)中。Δ为力的变化量，对应于式(7)中。

2.2 切削液的刚度系数与阻尼系数

钻杆在加工过程中与切削液的相互作用如图1所示。

图1 钻杆与切削液相互作用示意图

使用雷诺方程计算切削液的刚度与阻尼系数[5]：

(8)

(9)

从式(9)中可以得到切削液的压力表达式[6]。结合式(6)和(7)对结果进行分析，则刚度、阻尼的表达式如下：

(10)

其中，Φa和Φb表示切削液压力区域的起始和终止角度。

3 BTA深孔钻运动轨迹方程

如图1所示，在切削液的作用下，BTA钻杆理想中心o的位置在(x，y)，实际中心o1的位置在(x1，y1)。如果钻杆的刚度系数是k，o的微分方程：

(11)

钻杆弹性力与切削液反作用力之间的平衡条件是：

(12)

则切削液作用力的线性表达式为：

(13)

假设解的形式为x=x0e(σ+iω)t，y=y0e(σ+iω)t，x1=x10e(σ+iω)t，y=y10e(σ+iω)t，其中σ和ω可以通过式(11)～(13)计算获得。根据Floquet原理，钻杆发生失稳的边界条件是σ=0，所以将式(10)代入式(11)，通过计算可以得到钻杆实际中心的运动轨迹方程：

(14)

从式(14)可知：钻杆的运动轨迹与钻杆转速和涡动频率有关,使用Matlab对式(14)进行计算，以φ=23 mm的BTA钻为例，根据文献[7]可知，加工孔径为25 mm的孔，钻杆转速为10 rad·s-1时，则钻杆的轨迹根据不同的涡动频率不同，其形状如图2所示。

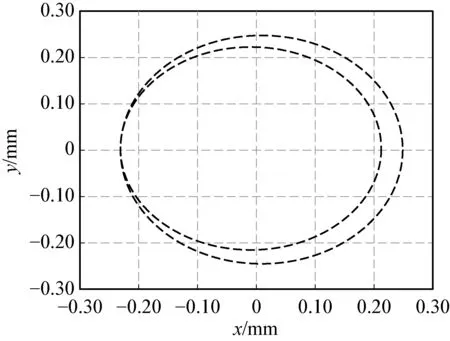
(a) 涡动频率为5 rad·s-1 (b) 涡动频率为10 rad·s-1

(c) 涡动频率为20 rad·s-1 (d) 涡动频率为30 rad·s-1

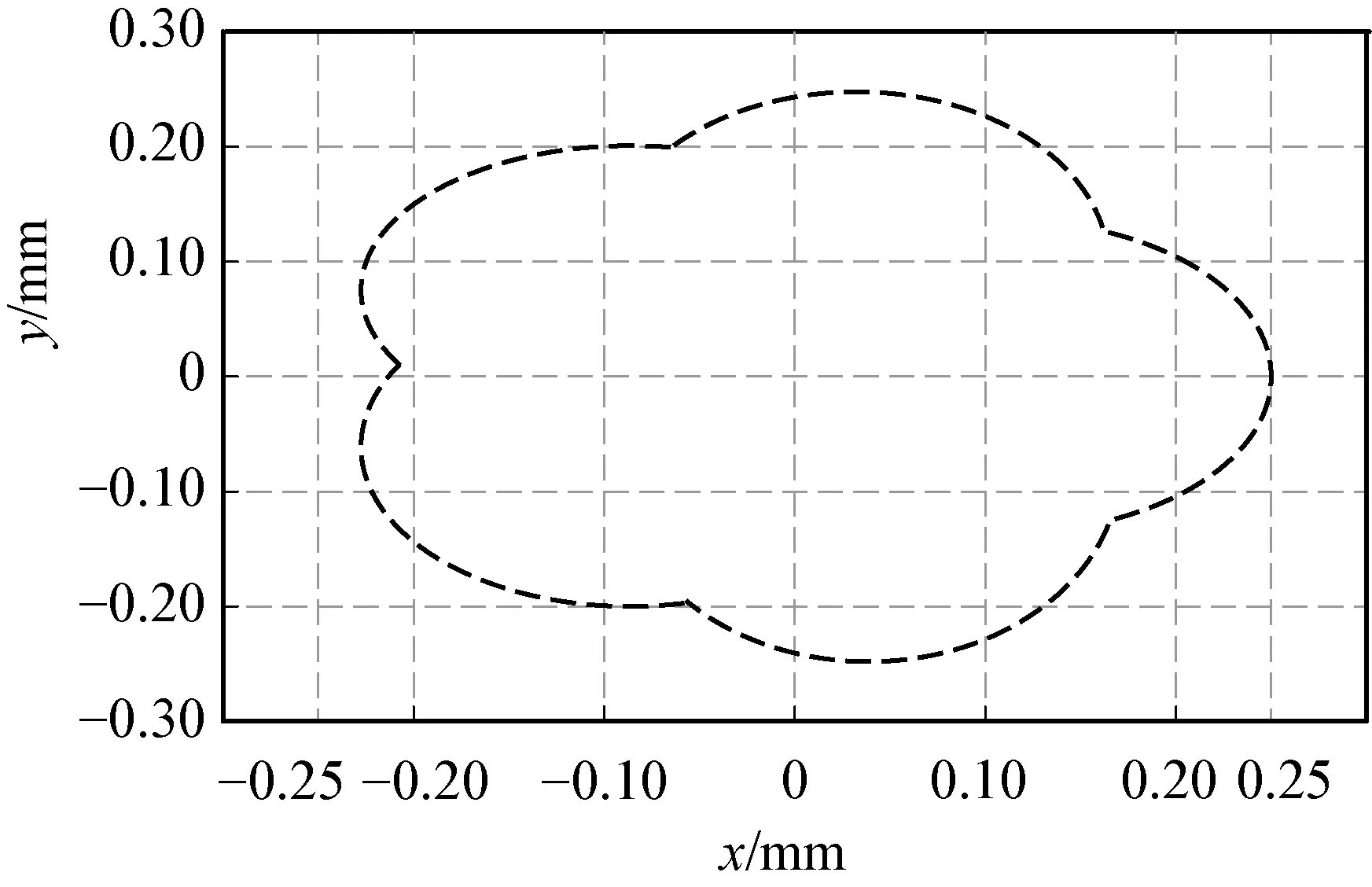
(e) 涡动频率为50 rad·s-1 (f) 涡动频率为60 rad·s-1

由图2可知：钻杆发生失稳现象的临界值为20 rad·s-1，即当钻杆涡动频率小于钻杆转速的2倍时，钻杆的运动轨迹为椭圆形，当涡动频率大于转速的2倍时，涡动轨迹呈现多凸角形式，且凸角数等于涡动频率与转速比值减1。所以在加工过程中，适当增加转速有利于提高钻杆涡动的稳定性。

4 结 论

本文根据BTA深孔加工过程中的实际情况，对钻杆涡动进行研究。使用Timoshenko梁模型对BTA系统进行建模，并加入切削液的影响，建立耦合模型。通过研究切削液对钻杆系统的影响规律，建立了BTA钻杆中心的运动轨迹方程。计算结果表明：钻杆的涡动频率与转速之间的比值是影响钻杆涡动稳定性的指标，且比值为2是稳定性的临界条件。稳定的涡动形状为椭圆形，不稳定的涡动形状为多凸角形状，且凸角个数为比值减1。