基于MCEM算法的多元正态分布均值向量估计

2022-08-17殷雨晨陈兆荣

宁夏师范学院学报 2022年7期

殷雨晨,陈兆荣

(铜陵学院经济学院,安徽铜陵 244000)

在数据收集和处理的过程中,往往会出现数据缺失的现象,不恰当的处理方法将会影响分析结果的可靠性.因此,如何在数据存在缺失的情况下减小估计的误差成了亟待解决的问题.对于缺失的数据,利用数据特征来进行填补是目前统计学中最常用的方法,包括均值插补法、回归插补法和最近距离插补法等.其中,均值插补法就是用所研究样本的已观测数据的均值作为缺失值的替代值,这种方法操作简单,实用性强.不过也存在着明显的弊端,即均值填补忽略了数据的离散程度,可能会造成较大的推断误差.

除了进行传统的方法进行数据填补以外,EM(Expectation Maximization)算法也逐渐被应用到经济、医疗和工程等不完全数据的处理中.孙大飞[1]将EM算法应用到混合密度极大似然参数估计当中,验证了此算法的收敛性和有效性.张梦琇[2]将EM算法应用到左截断右删失数据的几何分布参数估计中.此外,学者们也对EM算法不断进行研究和改进,先后提出了ECM(Expectation Conditional Maximization)、ECME(Expectation Conditional Maximization Either)、PX-EM(Parameter-Expanded EM)和MCEM(Monte Carlo EM)等算法.温艳清[3]在区间型数据条件下利用ECM算法对Weibull分布进行了极大似然估计.严海芳[4]应用MCEM算法给出了对数正态分布的参数的迭代公式,给出了比EM算法更有效、收敛速度更快的模拟结果.本文将MCEM算法引入到含缺失数据的多元正态数据的均值向量估计当中,得到迭代公式,并据此进行数值模拟,验证算法的合理性和准确性.

1 EM算法和MCEM算法简介

EM算法,也称最大期望算法,是一种能够在不完全数据下通过迭代得到参数最大似然估计的算法,最早由Dempster[5]提出,该算法迭代速度较快并且估计结果具有很好的稳定性.它是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量.EM算法的每次迭代包括一个E步和一个M步,两个步骤交替进行计算.其基本思想是:首先根据已经给出的观测数据,估计出模型参数的值;然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前已经观测到的数据重新再对参数值进行估计,然后反复迭代,直至最后收敛,迭代结束.

E步:计算目标Q函数

Q(θ|θ(t))=Ef[l(θ|Yobs,Ymis)|Yobs,θ(t)]

(1)

M步:求目标Q函数的最优解

θ(t+1)=argmaxQ(θ|θ(t))；

(2)

E2步:计算目标Q函数,其中

(3)

M步:求目标Q函数的最优解

θ(t+1)=argmaxQ(θ|θ(t))；

(4)

2 含缺失数据的多元正态数据的MCEM算法

2.1 多元正态分布的定义

多元正态分布是一元正态分布的推广[7].已知一元正态分布的密度函数为

(5)

将式(5)进行推广,可以给出多元正态分布的定义

定义1p元正态变量X=(X1,X2,…,Xp)′的概率密度函数为

(6)

其中,|Σ|为协方差阵Σ的行列式.

2.2 多元正态分布的条件分布

记X～Np(μ,Σ),将X,μ和Σ剖分如下

其中,X(1),μ(1)为q×1维,Σ11为q×q维,(X(1)|X(2))为给定X(2)时X(1)的条件分布[8].

定理1 设X～Np(μ,Σ),Σ>0,则

(X(1)|X(2))～Nq(μ1·2,Σ11·2),

其中

(7)

(8)

2.3 二元正态分布均值的MCEM估计

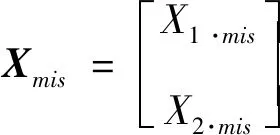
(9)

(10)

最后实现M步,对目标函数求极值

(11)

(12)

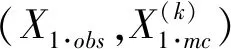
3 MCEM算法的数值模拟

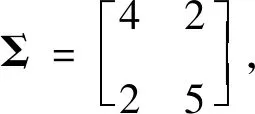
由表1可知,相比于传统的均值插补法,MCEM算法估计的均值离真实值的偏差更小,效果更好.并且随着样本量的增大,MCEM算法的估计精度也有所增加,即当样本量从100增加到1000时,μ1估计偏差的绝对值从0.3938降低到0.0351,μ2估计偏差的绝对值从0.1198降低到0.0721.因此,本文提出的MCEM算法比均值插补法更有优势,在多元正态分布的均值向量估计中是切实可行的.