基于Legendre变换的最优再保险投资策略

陈子旸，王秀莲

(天津师范大学 数学科学学院， 天津 300387)

经典Cramér-Lundberg风险模型自Lundberg首次提出以来，相关问题在精算科学中受到了学者们的广泛关注，大部分文献都假设保费率为常数，如文献[1-3]按照期望保费原则和方差保费原则厘定保费。但对保险公司来说，索赔和保费率是密切相关的，针对这一问题，很多学者对经典的Cramér-Lundberg模型进行改进，考虑索赔率不是常数的情况，如文献[4]研究保费率和索赔率存在一个严格单调的关系下的相关问题，文献[5]研究随机保费和交易费用下的最优投资再保险投资问题。上述保费原则均是在事故发生后进行赔偿，即与未来索赔有关，但对于主观因素较多、损失变动幅度较大的风险，如公众责任保险，厘定费率时仅考虑未来索赔而忽略历史索赔未必是合理的。文献[6]证明了对于保险公司来说，未来索赔与历史索赔是相关的。所以重视相关索赔可以更好地帮助保险公司规避未来的风险，但这方面的研究相对较少。文献[7]第一次提出采用外推偏差测量相关索赔。文献[8]在文献[7]的基础上对外推偏差进行拓展，定义外推期望，用历史索赔和索赔期望的初始估计的加权平均预测未来索赔的期望，在最大化终端财富的期望指数效用和均值-方差效用的目标下，得到最优再保险策略的解析表达式。文献[9]在文献[8]的基础上，增加了金融市场、保险市场的不确定性并且投资了有风险资产，得到了稳健的最优再保险投资策略。

众所周知，金融和保险在社会中越来越重要，许多学者把风险理论和金融数学结合起来，研究了随机控制优化问题，如最优分红、最优投资和最优再保险问题。特别地，再保险参与下的最优投资问题引起了许多学者的关注。文献[10]在Heston模型下考虑投资有风险资产，研究具有跳-扩散风险过程的最优超额损失再保险投资问题。文献[11]基于带漂移系数的盈余过程，考虑投资价格由CEV模型决定的风险资产，在最大化终端财富分数幂效用的目标下，用随机方法确定最优再保险投资问题。文献[12]研究复杂随机环境下具有错误定价和模型不确定性的保险公司的优化问题，在Ornstein-Unlenbeck模型下定义股票的瞬时收益率，通过动态规划原理，导出了以最大化指数效用函数为目标的稳健最优投资再保险策略的解析解。

根据随机控制理论得到的Hamilton-Jacobi-Bellman(HJB)方程通常是非线性偏微分方程，这类方程一般难以得到解析解，而应用Legendre变换可以把最初问题转化为对偶问题，进一步求解线性偏微分方程得到对偶问题的解析解，为最优策略提供了现实意义。文献[13]利用CEV模型研究了固定缴费型养老金计划，通过Legendre变换和对偶理论给出了在退休前后两个时期的最优投资策略。文献[14]研究在Vasicek模型下最大化HARA效用，利用Legendre变换得到最优消费和投资策略的解析解。文献[15]采用期望保费原则收取保费，在CEV模型和Legendre变换下最大化终端财富期望对数效用，得到最优再保险投资策略的解析表达式。

本文在文献[15]的基础上，将相关索赔保费原则考虑进费率定价过程中，考虑在最大化终端财富期望下的最优投资再保险问题，在对数效用目标下，借助Legendre变换得到最优再保险投资策略。

1 模型构造

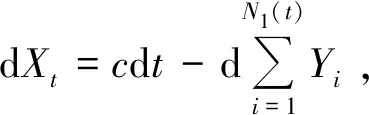
(1)

其中W1(t)是标准的布朗运动。有大量的研究可以表明(如文献[6，16])未来索赔与历史索赔是相关的，那么可以合理地假设保险公司认为索赔的历史趋势能预测未来索赔的变化，借鉴文献[9]，用外推偏差v(t)衡量相关索赔，

(2)

其中v(0)=v0=0，δ是外推强度(0<δ<1)，并且dL(s-ds)=L(s)-L(s-ds)代表从时刻s-ds到时刻s发生的索赔数量。

为确保历史索赔的加权平均是有限的，假设|v(t)|≤M，0≤t≤T，其中M是一个正的常数。对式(2)求导，得到：

dv(t)=-δv(t)dt+δdL(t)。

通过相关索赔保费原则，累计索赔过程(1)的微分形式为

因此

保险公司为了避免更大的风险，采取的再保险类型设为比例再保险，t时刻的自留比例为a(t)，0≤a(t)≤1，即保险公司支付每份索赔额的a(t)，相应的再保险公司支付余下的1-a(t)。为避免套利，保险公司购买再保险的保费率为c1=(1+η2)(e-δtλ1μ11+v(t))，其中η2为再保险公司的安全负荷且η2>η1。因此在购买再保险之后，在t时刻保险公司盈余过程为

保险公司为了资金运转，在金融市场投资无风险资产P0(t)和有风险资产P1(t)，无风险资产P0(t)的定价过程为

dP0(t)=rP0(t)dt，

其中r>0为无风险利率。有风险资产P1(t)的定价过程为

dP1(t)=αP1(t)dt+βP1(t)dW2(t)，

其中α>0，β>0，W2(t)是标准的布朗运动且W1(t)与W2(t)独立。假设保险公司在t时刻投资在风险资产的数量为π(t)，那么在再保险投资策略Π=(a(t)，π(t))下，对应于保险公司的盈余过程表示为

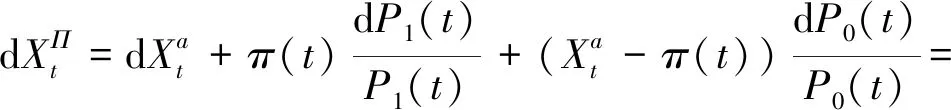
(3)

定义1 称Π={(a(t)，π(t))t≥0}为可行策略，如果Π中元素满足如下条件：

(1) ∀t>0，(a(t)，π(t))是关于{Ft}t≥0循序可测的；

(3) (a(t)，π(t))使式(3)有唯一的强解。

为方便起见，∀t≥0，令a(t)=a，π(t)=π，v(t)=v。

2 相关索赔保费原则下的最优策略

2.1 目标函数

假设V是一个效用函数，对于一个固定时间段[0，T]，定义

VΠ(t,v,x)=E[V(X(T))|v(t)=v，X(T)=x]，

应用随机控制定理，定义

本文目标是找到最优策略Π*，使H(t,v,x)=VΠ*(t,v,x)。由动态优化原理，得到H(t，v，x)满足的HJB方程[17]为

Ht+[rx+π(α-r)+(η1-η2+aη2)(e-δtλ1μ11+v)]Hx+δe-δtλ1μ11Hv+

(4)

且有边界条件H(T，v，x)=V(x)。

根据一阶最优条件，对式(4)关于a和π求导，得到

(5)

再把式(5)代入式(4)得到

(6)

由于方程(6)是非线性偏微分方程，所以利用Legendre变换将其转化为对偶问题，通过求解对偶问题得到原问题的解析解。

2.2 对偶问题

利用值函数的凸性定义如下的Legendre变换：

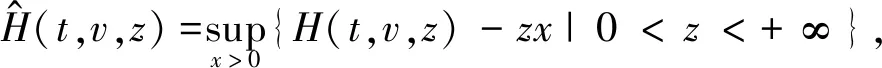
其中z是x的对偶变量。x的值表示为g(t，v，z)，因此

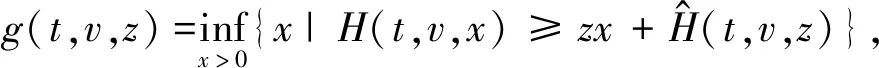
根据上面的表达式，

(7)

在终点时间T，定义

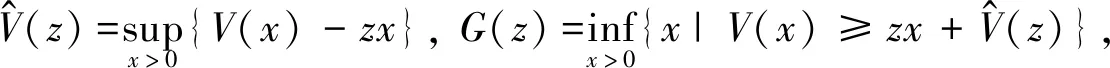
(8)

对应的边界条件为g(T，v，z)=(V′)-1(z)。

因此最初的问题转化为对偶问题。

把式(7)代入式(6)并关于z求导得到

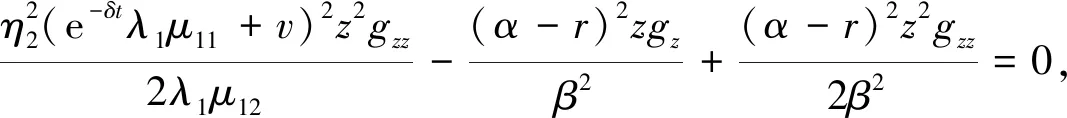
(9)

把式(7)代入式(5)得到最优策略

(10)

因此，对于原问题，通过求解g的线性偏微分方程并从其一阶导数中确定最优策略a*和π*。

选择如下的对数效用函数：

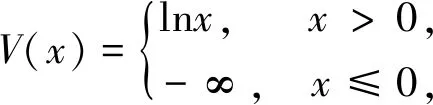
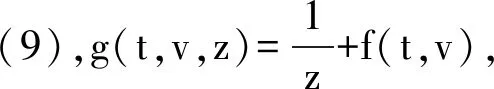
f(t,v)=B(t)v+D(t)，

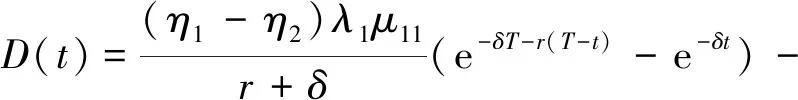
对应的最优再保险和投资策略为

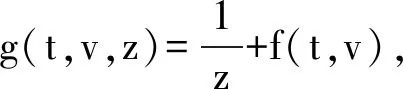
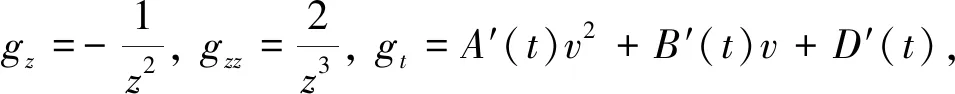
gv=2A(t)v+B(t),gvv=2A(t),gvz=0,

(11)

把式(11)代入式(9)，得到

[A(t)(r-2δη2)-A′(t)]v2+[B(t)(r-δη2)+(η1-η2)-B′(t)]v+D(t)r+

(η1-η2)e-δtλ1μ11-D′(t)-δe-δtλ1μ11B(t)-δη2e-δtλ1μ11B(t)=0,

令v2、v、常数项的系数为0，又因为边界条件A(T)=0，B(T)=0，D(T)=0，可得

A(t)=0，

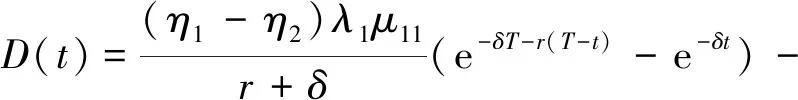
最后将式(11)代入式(10)，得到最优再保险和投资策略的解析解：

证毕。

3 无相关索赔保费原则下的最优策略

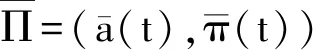
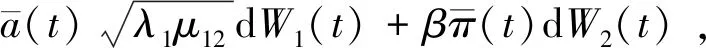
(12)

最优再保险和投资策略为

(13)

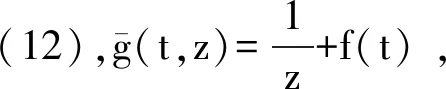
对应的最优再保险和投资策略为

本定理的证明过程与定理1类似，这里不再赘述。

注 将式(10)和式(13)进行对比，最优再保险和投资策略既有区别又有相同之处。的形式更简单，随着η2的增加，a*和都将增加，即保险人愿意通过自己的努力控制风险。π*和是一样的，因为再保险市场和金融市场之间没有相关性，不论考虑相关索赔与否，都不会改变投资策略。

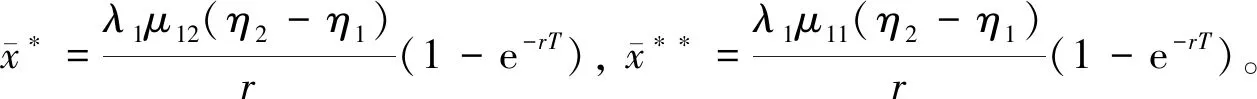
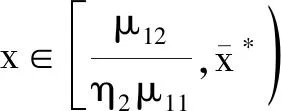
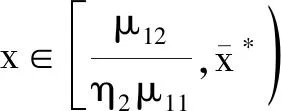
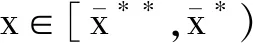
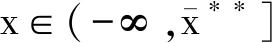
证毕。

4 数值例证

本节分析模型参数对相关索赔原则下的最优投资再保险策略的影响。

在保险市场中，取η1=0.02，η2=0.04，λ1=1，δ=0.12，μ11=1，μ12=1，x=5，v=0.4。在金融市场中，取α=0.04，β=0.5，r=0.02。其他参数取t=0，T=10。

图1和图2给出了外推强度δ对最优再保险a*(t)和最优投资π*(t)的影响。a*(t)与δ呈正相关，这意味随着δ的增加，加权平均v(t)也增加。v(t)与财富过程的风险呈负相关，这说明保险公司面临的风险越少，进而减少对再保险业务的需求，提高风险自留比例。相反地，π*(t)与δ呈负相关，这表明随着δ的增加，保险公司自留比例提高，所以将把更多的资金用于保险业务，减少对风险资产的投资。

图3给出了再保险公司的安全负荷η2和外推强度δ对自留比例a*(t)的共同影响。通常情况下，η2越大，保险公司的自留比例越大，购买再保险量越少，但有外推强度δ的存在，保费根据最近索赔情况，为了减少风险，会增加风险转移，即降低自留比例。图4表明加权平均v(t)越大，保险公司风险自留比例越高，因此再保险需求越少。表明v(t)越大，意味着保险公司可以收取更多的保费，有足够的支付能力来应对未来的索赔。

图1 δ对a*(t)的影响 图2 δ对π*(t)的影响

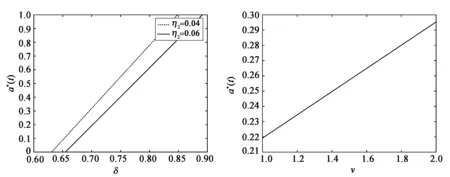
图3 δ和η2对a*(t)的影响 图4 v对a*(t)的影响

5 结论

本文中，保险公司购买比例再保险，同时进行有风险与无风险两种投资方式。保险公司与再保险公司在相关索赔原则下采用不同的参数定价费率，其相关索赔通过一个外推偏差测量。在最大化保险公司终端财富对数效用的目标下，根据随机控制理论，应用Legendre变换解决目标函数的初始问题，求出了两种保费原则下最优再保险投资策略的解析式。在无相关索赔原则下，划分了终端财富的区域，确定了再保险a*等于0和1的特殊情况。通过实例分析了模型中的参数对最优策略的影响。发现，外推强度δ在最优策略中起着重要作用，所得结果符合我们的直观理解。在本文的基础上，可以进一步考虑模型在不确定性下的最优问题，以及考虑保险市场和金融市场在相关性下的最优鲁棒投资策略。