基于GRA和GA-BP神经网络的商品住宅需求预测

邓 英，邹 璐，田学泽

(1.长沙理工大学 经济与管理学院， 湖南 长沙 410114；2.长沙理工大学 交通运输工程学院， 湖南 长沙 410114)

当前城镇化进程的快速推进使得商品住宅需求过旺，房地产住宅市场供求结构关系严重失衡，人民日益增长的住房需求同发展不平衡的商品住宅市场间的矛盾愈演愈烈。因此，识别影响商品住宅需求的主要因素，构建符合房地产住宅市场现状的商品住宅需求预测指标体系，建立预测精度高的商品住宅需求预测模型开展商品住宅需求预测，对促进商品住宅供给科学决策、恢复房地产住宅市场供求结构关系平衡乃至推进商品住宅市场走可持续健康发展道路具有十分重大的意义。

纵观当前国内外学者在商品住宅需求预测上的研究现状，研究内容主要有两个方面——商品住宅需求预测方法的研究与预测数据的选择。

关于商品住宅需求预测的方法主要分为以下几种：(1)以计量统计学为基础的传统预测方法，主要有时间序列分析法[1-2]、多元线性回归模型、灰色理论模型与马尔科夫链模型等[3-7]；(2)以机器学习算法和计算机技术为基础的智能预测方法，主要有反向传播(Back Propagation，BP)神经网络模型、径向基函数(Radial Basis Function，RBF)神经网络模型、支持向量机(Support Vector Machine，SVM)模型、基于粒子群优化算法改进反向传播(Particle Swarm Optimization-Back Propagation，PSO-BP)神经网络模型等[8-11]。

关于预测数据的选择可分为两类：一类是选取与商品住宅需求量关联度较高的影响因素作为自变量，并以其历史数据为数据源，通过建立线性或非线性模型对其商品住宅需求量进行预测，例如，文献[12]和文献[8]分别在采用主成分分析法与邻域粗糙集提取影响商品住宅需求量主要因素的基础上，结合其历史统计数据资料，通过BP神经网络模型对其商品住宅需求量进行了预测；另一类是直接以商品住宅需求的历史数据为数据源，通过建立模型对其商品住宅需求量进行时间序列上的预测，如文献[13]以石家庄市2000—2012年的商品住宅需求量为数据源，采用GM(1,1)模型对其未来5年的商品住宅需求量进行了预测。

由上述分析可知，随着计算机技术与机器学习算法的快速发展与推广，采用机器学习算法结合计算机技术开展预测研究已成为热潮，以计量统计学为基础的传统预测方法已失去优势。此外，考虑到以影响商品住宅需求关键因素的历史数据作为预测数据源要优于直接以商品住宅需求历史数据作为预测数据源，本文将灰色关联分析法(Grey Relational Analysis，GRA)、遗传算法(Genetic Algorithm，GA)与BP神经网络方法相结合，建立基于GRA和GA-BP神经网络的商品住宅需求预测模型；然后以湖北省黄石市为例，结合房地产住宅市场现状与2006—2020年统计年鉴数据开展实证研究，以期为科学合理预测商品住宅需求量提供新方法。

1 传统预测方法

1.1 灰色关联分析法

灰色关联分析法(GRA)是一种适用于在复杂变量因素系统中以定量研究视角，分析多个变量对目标属性变量影响程度的方法[14]。该算法的核心思想是通过计算各影响因素与目标属性变量之间的关联度值，依据灰色关联度值来表达各因素对目标属性变量影响程度的大小，进而使分析结果更为直观清晰，具体实施步骤如图1所示。

图1 灰色关联分析流程图

1.2 遗传算法

遗传算法(GA)是一种效仿自然选择机制和生物进化原理，且具有随机性的新型全局搜索算法。该算法的主要机理是在种群进化的过程中以优胜劣汰的方式选取适应度较高的种群进行交叉、重组与变异，以产生新的子种群，如此不断循环迭代便可进化出最优的个体[15]。图2为遗传算法基本流程图。遗传算法最大的优势在于其不受制于目标函数的类型，具有计算速度快与全局收敛性好等优点。

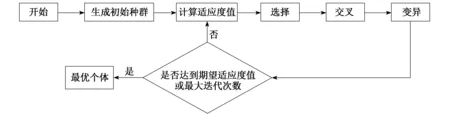
图2 遗传算法基本流程图

1.3 BP神经网络法

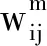
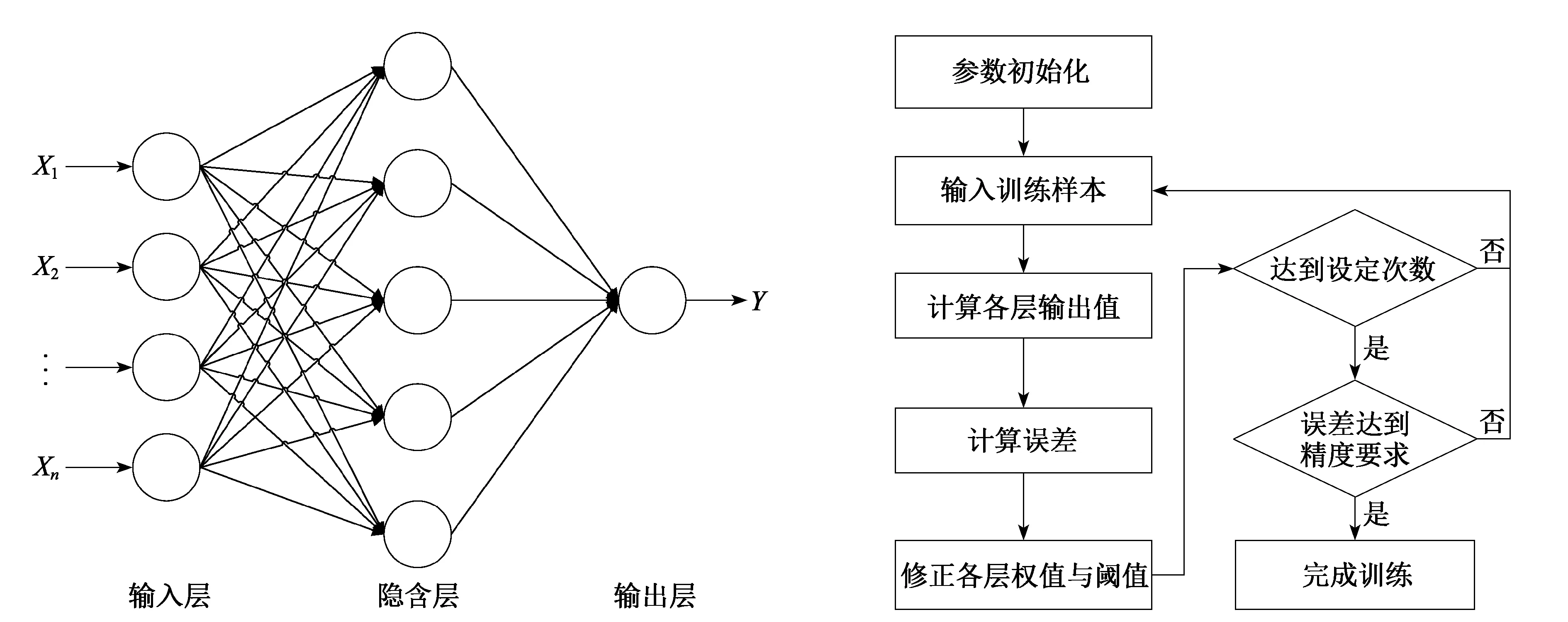
图3 BP神经网络拓扑结构 图4 BP神经网络算法学习流程图

输出层的误差可以表示为

(1)

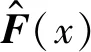
(2)

(3)

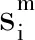
2 基于GRA和GA-BP神经网络的商品住宅需求预测模型的建立

本文在建立商品住宅需求预测模型时，首先，在识别和选取商品住宅需求影响因素的基础上，运用灰色关联分析法(GRA)提取影响商品住宅需求的主要影响因素，并以此构建商品住宅需求预测指标体系；其次，将已构建的商品住宅需求预测指标体系作为BP神经网络的输入向量，商品住宅销售量作为输出变量建立预测模型；但由于BP神经网络具有收敛速度慢、全局搜索能力弱与易出现局部最小值等缺点。故先引用遗传算法(GA)对BP神经网络的各层权值与阈值进行全局寻优，再运用经GA优化后的BP神经网络开展预测。GA优化BP神经网络的基本流程如图5所示，具体步骤如下：

第1步：种群初始化与个体编码。随机生成初始种群后，以实数编码的方式对个体进行编码，个体编码的内容为BP神经网络的权值与阈值。

第2步：选择适应度函数。依据对个体进行编码所得到的BP神经网络初始权值与阈值，采用训练样本数据对BP神经网络进行训练，将网络输出值与真实值之间的均方根误差(Root Mean Square Error，RMSE)作为适应度函数。BP神经网络的适应度值与输入个体的适应度值正相关，其适应度值与预测误差负相关。因此，在计算得出所有个体的适应度值后，选择适应度值最大的个体作为子种群。

第3步：选择操作。通常遗传算法实施选择操作的算子有轮盘赌法和锦标赛法，本文选择轮盘赌法作为遗传算法的选择算子，其原理是依据适应度比例进行选择，每个个体i被选中的概率为

(4)

其中fi=k2/Fi表示个体i的适应度值，k2为常系数，N表示种群个体数量，Fi表示个体i的误差值。

第4步：交叉操作。采用实数交叉法实施交叉操作，若第k个染色体ak和第i个染色体ai分别与第j个基因进行交叉，则交叉操作方法如

(5)

式中b为取值在[0,1]的随机数。

第5步：变异操作。变异操作可利用均匀变异算子实现，如第i个个体的第j个基因可按式(6)和式(7)实施变异操作：

(6)

(7)

其中amax和amin分别表示基因aij的上下界，g为适应度误差值，gmax为适应度误差的最大值。

第6步：计算适应度值。依据每次迭代所得适应度值是否满足精度或是否已达到最大迭代次数判断是否满足迭代停止条件，若满足条件则输出最优权值与阈值，否则继续循环迭代。

第7步：实施预测。将最优权值与阈值输入BP神经网络模型，对测试样本数据实施预测。

图5 遗传算法优化BP神经网络流程图

3 商品住宅需求影响指标体系构建

商品住宅需求是指在一定时期内消费者愿意且能够购买的商品住宅数量，通常以商品住宅销售面积来衡量住宅需求量的大小[20]。商品住宅需求系统是一个复杂的非线性系统，在分析其影响因素时需结合与之相关的经济、政策、人口及社会等因素，因此，本文从经济性因素和非经济性因素两方面识别与选取影响黄石市商品住宅需求的因素，并采用灰色关联分析法筛选与商品住宅需求量关联性强的因素，以此构建黄石市商品住宅需求影响指标体系。

3.1 影响因素的识别与选取

从经济性因素和非经济性因素两方面识别与选取影响黄石市商品住宅需求因素时，考虑到指标因素的可获取性与可量化性，在分析现有研究成果的基础上，结合黄石市房地产发展现状与2006—2020年统计年鉴数据，选取城镇人口数量(X1)、城镇化率(X2)、城镇居民人均GDP(X3)、城镇居民储蓄存款余额(X4)、房地产开发投资额(X5)、商品住宅销售均价(X6)、住宅施工面积(X7)、住宅竣工面积(X8)、住宅新开工面积(X9)、城镇居民人均可支配收入(X10)、城镇居民人均消费性支出(X11)、城镇居民人均居住面积(X12)、城镇居民恩格尔系数(X13)、城镇居民家庭平均每户人口数(X14)、城镇居民家庭人均住房贷款偿还金额(X15)、城镇居民家庭人均缴纳住房公积金金额(X16)共16个指标为黄石市商品住宅需求影响因素，且以住宅销售面积(Y)来表征商品住宅需求量，具体数据见表1。

表1 2005—2019年黄石市商品住宅需求影响因素数据

3.2 关键影响因素筛选

考虑到已识别与选取的影响因素间存在量纲差异，会导致关联性分析结果产生较大误差，在分析各影响因素与商品住宅需求间关联性的强弱前，先对各影响因素进行无量纲处理。通常，采用式(8)对指标因素进行无量纲化处理：

(8)

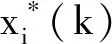
运用式(8)对表1中的各影响指标的数值进行无量纲化处理后，利用灰色关联分析法对商品住宅需求与16个影响因素进行相关性分析，分析结果见表2和图6。依据灰色关联分析原理，若灰色关联度值大于0.7，则表示影响因素与目标变量具有强相关性。

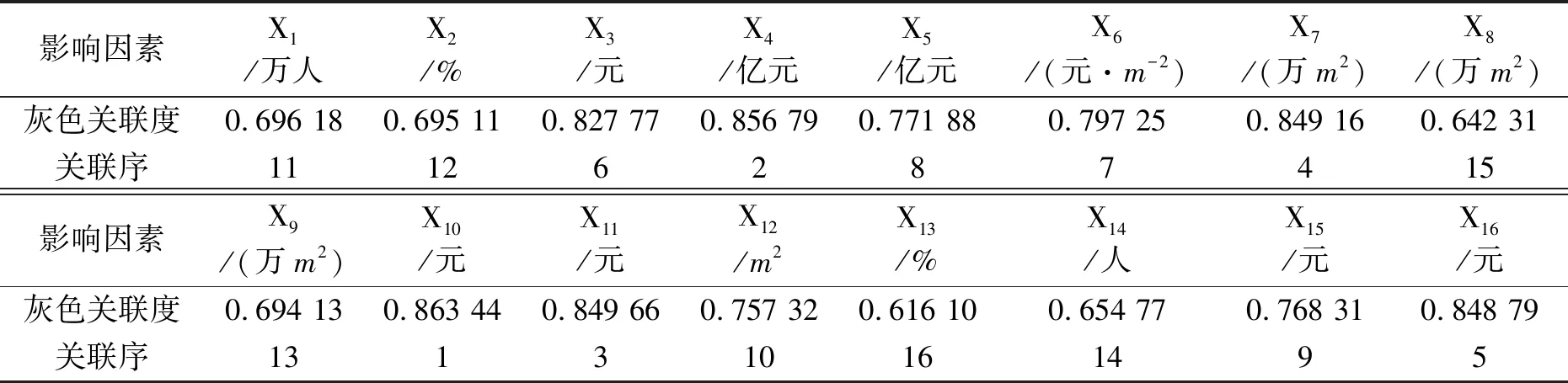
表2 黄石市商品住宅需求与各影响因素间的灰色关联度

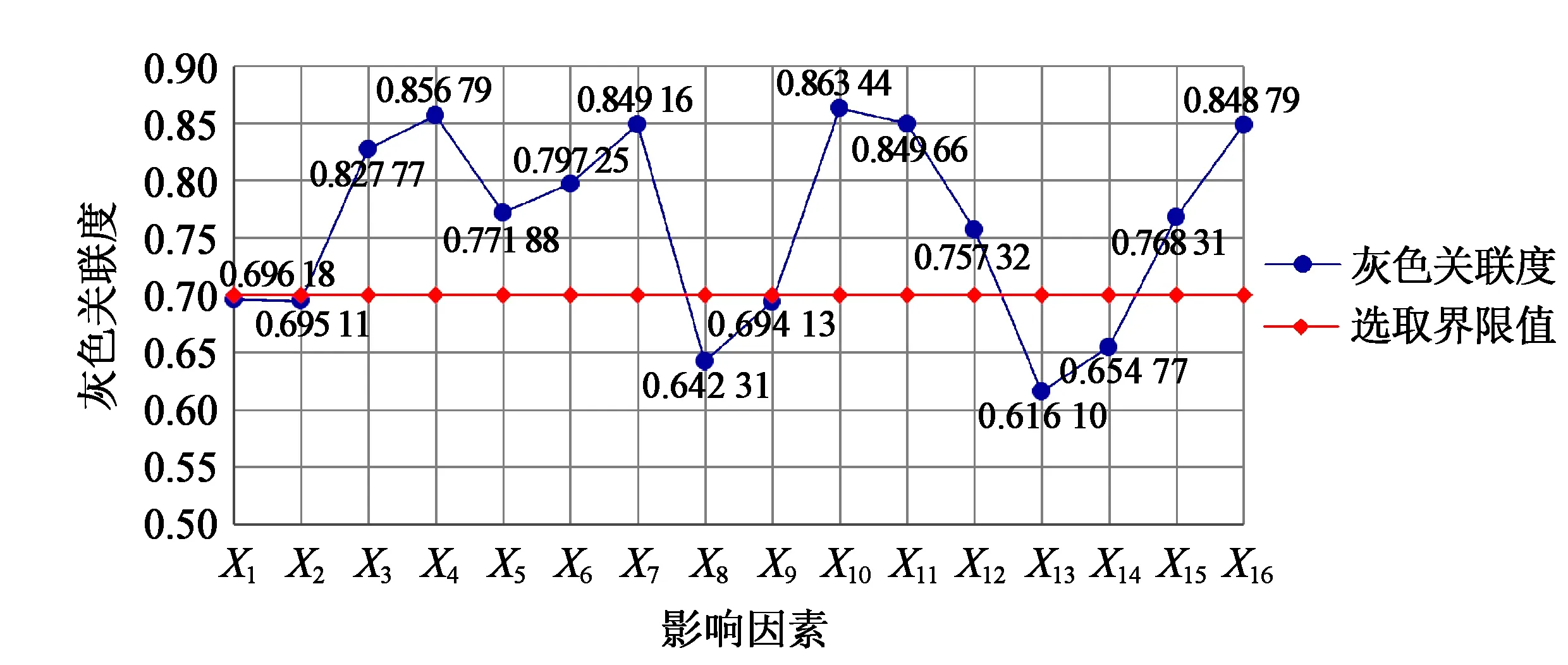
图6 各影响因素灰色关联度结果

由表2和图6可知，城镇居民人均可支配收入(X10)、城镇居民储蓄存款余额(X4)、城镇居民人均消费性支出(X11)、住宅施工面积(X7)、城镇居民家庭人均缴纳住房公积金金额(X16)、城镇居民人均GDP(X3)、商品住宅销售均价(X6)、房地产开发投资额(X5)、城镇居民家庭人均住房贷款偿还金额(X15)、城镇居民人均居住面积(X12)等因素与黄石市商品住宅需求的灰色关联度均大于0.7。因此，本文选取以上10个指标为影响黄石市商品住宅需求的主要因素，并以此构建黄石市商品住宅需求预测指标体系，详细数据见表3。

表3 黄石市商品住宅需求预测指标体系

4 仿真实验分析

4.1 实验环境设计

本文运用MATLAB软件实施仿真实验研究，BP神经网络的拓扑网络结构使用典型的3层结构模式，训练函数使用L-M优化算法trainlm，传递函数使用purelin函数和logsig函数；遗传算法(GA)的种群大小设为20，遗传代数设为100，交叉概率与变异概率分别设为0.6和0.01，适应度函数为RMSE，BP神经网络与遗传算法(GA)的具体参数设置见表4。

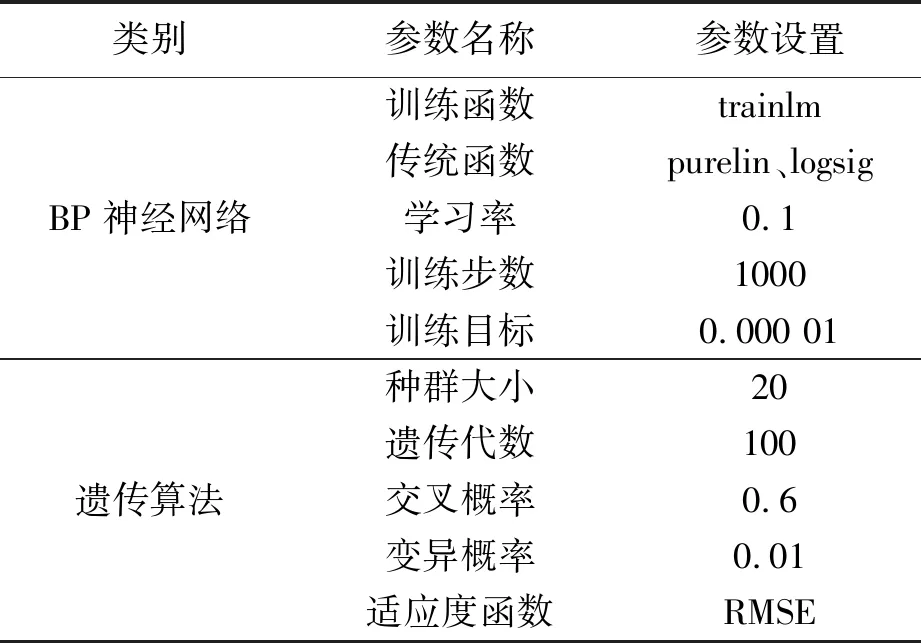
表4 BP神经网络与遗传算法参数设置

4.2 数据处理

为了避免由于数据量纲的差异给BP神经网络学习效率及预测精度带来的不利影响，本文调用MATLAB R软件中的mapminmax函数对表3中的数据进行归一化处理，归一化后的数据见表5。

表5 预测指标体系归一化后的数据

4.3 模型建立

将表5中的数据输入GA-BP神经网络模型，随机选取10个为训练样本，其余为测试样本，并利用训练集样本对GA-BP神经网络进行训练。经反复训练获得GA-BP神经网络模型的最优迭代误差曲线变化图、训练集样本预测值与真实值的对比图，如图7所示。

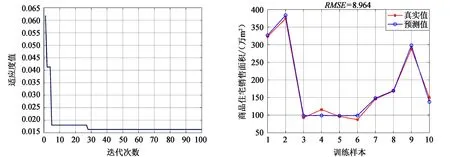
(a)GA-BP模型迭代误差图 (b)GA-BP模型训练效果图图7 GA-BP神经网络模型建立

由图7(a)可知，随着遗传算法迭代次数的增加，适应度值不断趋于稳定，当迭代至第28代时，遗传算法对BP神经网络的权值与阈值寻优及BP神经网络模型精度训练结束，此时适应度值为0.015 2，满足要求。结合图7(b)可知，经训练集样本训练后的GA-BP神经网络模型具有较高的线性拟合精度，且在训练集样本中的预测值与真实值的平均相对误差为5.32%，均方根误差(RMSE)为8.964，均满足要求。GRA和GA-BP神经网络模型建立完成。

4.4 模型应用与精度分析

为了验证GRA和GA-BP神经网络模型的有效性，将建立并训练完成的网络应用于黄石市商品住宅需求预测测试集样本的仿真预测，其仿真预测结果见表6，测试样本预测值与真实值的结果对比见图8。为进一步验证GRA和GA-BP神经网络模型预测能力的优越性，基于相同的输入数据，分别运用BP神经网络模型、多元线性回归模型(Multiple Linear Regression，MLR)、GM(1,1)模型与对黄石市商品住宅需求进行仿真预测，并将仿真预测结果与GRA和GA-BP神经网络模型预测结果进行对比分析。各模型预测结果及测试样本预测值与真实值的对比图见表6和图8，各模型测试样本预测结果平均相对误差与均方根误差见表7。

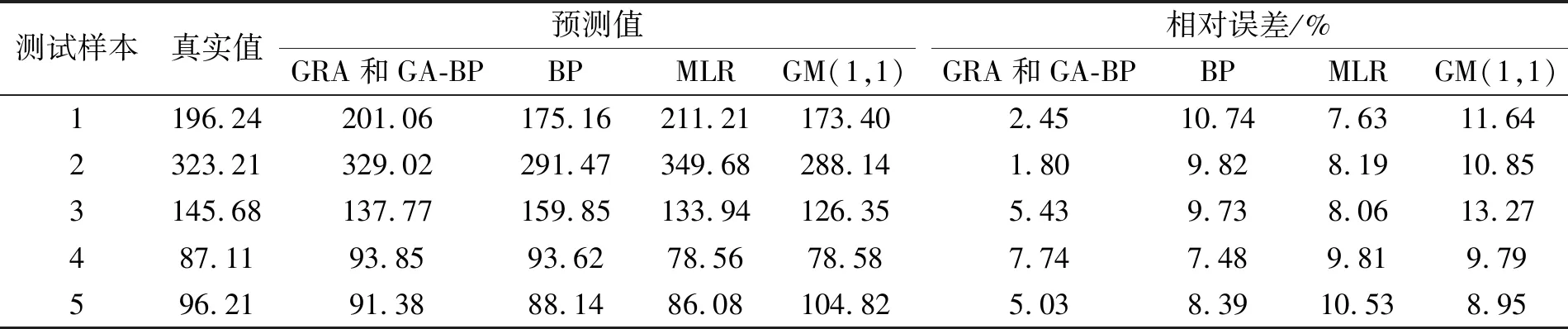
表6 各模型预测结果及误差

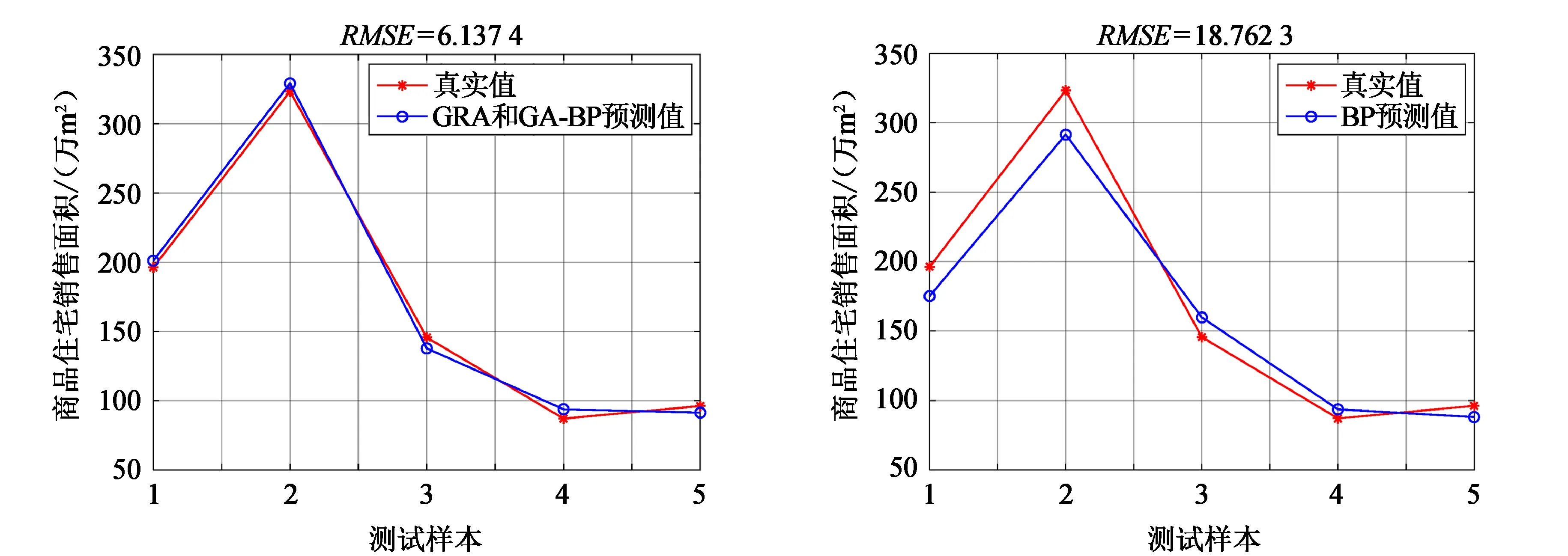
(a)GRA和GA-BP模型预测效果图 (b)BP模型预测效果图

(c)MLR模型预测效果图 (d)GM(1,1)模型预测效果图图8 各模型测试样本预测结果对比

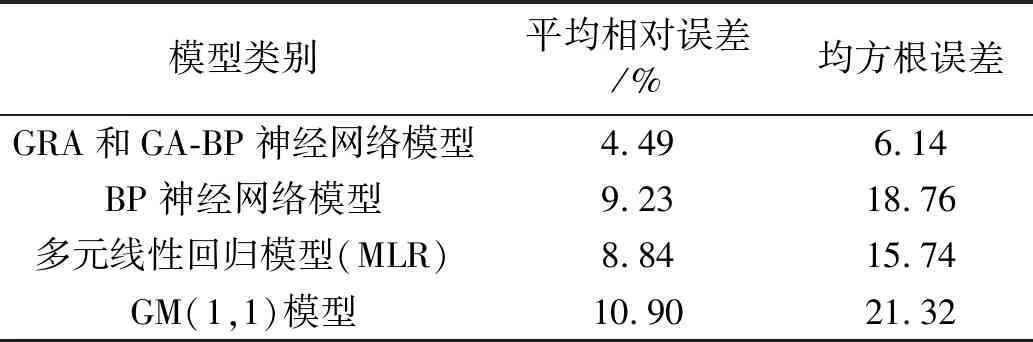
表7 各预测模型的统计误差

从图8可得知，GRA和GA-BP神经网络模型预测值曲线与测试样本真实值曲线基本吻合，拟合精度最优，仅在第4个测试样本处出现了些许偏差；BP神经网络模型预测值曲线与测试样本真实值曲线在前两个测试样本处偏差较大，后三个测试样本处偏差较小；多元线性回归模型(MLR)预测值曲线与测试样本真实值曲线在后三个测试样本处拟合相对较好，在其余两个测试样本处拟合较差；GM(1,1)模型预测值曲线与测试样本真实值曲线的拟合程度最差。

通过分析表6和表7可知，GRA和GA-BP神经网络模型的测试样本相对误差均在2%～8%范围内，且其测试样本的平均相对误差和均方根误差皆最小，分别为4.49%和6.14；虽然BP神经网络模型和多元线性回归模型(MLR)的测试样本相对误差皆位于7%～11%，且两者的测试样本平均相对误差与均方根误差都大于GRA和GA-BP神经网络模型，但多元线性回归模型(MLR)预测精度优于BP神经网络模型；GM(1,1)模型预测精度最差，测试样本相对误差位于9%～14%，测试样本平均相对误差和均方根误差分别为10.90%和21.32。因此，通过对比分析可知各模型的预测精度比较结果：GRA和GA-BP神经网络模型>多元线性回归模型(MLR)>BP神经网络模型>GM(1,1)模型。

综上所述，遗传算法用于BP神经网络的权值和阈值寻优切实可行，有利于提高BP神经网络模型的预测精度；本文构建的GRA和GA-BP神经网络模型适用于黄石市商品住宅需求预测，且预测精度高于其他预测模型。

5 结论

本文结合黄石市房地产市场现状与2006—2020年统计年鉴数据，将建立的GRA和GA-BP神经网络模型用于黄石市商品住宅需求预测分析，并将预测结果与BP神经网络模型、多元线性回归模型(MLR)及GM(1,1)模型进行对比，得出以下结论：

(1)从经济性因素与非经济性因素两个方面识别与选取16个黄石市商品住宅需求影响因素，将其与商品住宅需求进行灰色关联度分析。结果表明城镇居民人均可支配收入、城镇居民储蓄存款余额、城镇居民人均消费性支出、住宅施工面积、城镇居民家庭人均缴纳住房公积金金额、城镇居民人均GDP、商品住宅销售均价、房地产开发投资额、城镇居民家庭人均住房贷款偿还金额与城镇居民人均居住面积共10个因素灰色关联度大于0.7，因此，这10个因素为黄石市商品住宅需求的主要影响因素。

(2)在黄石市商品住宅需求测试样本的预测中，GRA和GA-BP神经网络模型测试样本相对误差的范围为2%～8%、平均相对误差为4.49%、均方根误差为6.14，与BP神经网络模型、多元线性回归模型(MLR)及GM(1,1)模型相比均最小；4种模型的预测精度比较结果：GRA和GA-BP神经网络模型>多元线性回归模型(MLR)>BP神经网络模型>GM(1,1)模型。

(3)通过对比GRA和GA-BP神经网络模型与BP神经网络模型的测试样本相对误差所处范围、平均相对误差值及均方根误差值可知，采用遗传算法对BP神经网络进行权值与阈值寻优切实可行，有利于提高BP神经网络预测精度。