基于广义多项式混沌法的圆柱壳自由振动不确定性分析

陈炉云,邓乃旗,杨 念

（1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.中国舰船研究设计中心，武汉 430064）

0 引 言

理论分析和数值计算是舰船结构声振特性预报的主要方法。对于舰船系统这样的复杂对象，即使实施精确的数字建模也存在一定的偏差，这些偏差不是由于设计或建造的错误因素所导致的，而是由结构固有属性所决定。由于存在着不确定性因素，结构响应参数仅是真实结果的近似值，两者间的偏差可能超出设计许可，并可能导致重大工程风险。在舰船结构建造过程中，存在着影响其声振特性的固有的、具有随机特性的影响参数，即建造因素不确定性。由于存在建造因素不确定性，使得舰船结构声振特性参数实质上是一个具有一定概率密度分布的随机变量，这表明在一定建造工艺水平下，不能消除该不确定性对系统的影响，即使提高工艺水平也只能使不确定性区间变窄而不能消除。建造因素不确定性包括材料参数不确定性、几何尺寸不确定性、边界条件不确定性、初始条件不确定性、操作环境不确定性、载荷不确定性等[1-4]。当结构中存在多个不确定性输入参数时，结构响应的预测值与实际值会存在巨大的偏差[5-7]。

对于结构声振特性不确定性问题，需评估各参数的不确定性对最终响应的影响，并用概率统计方法对这些影响进行描述以获得综合影响程度。针对已知概率密度分布的不确定性输入，采用数学模型将输入不确定性参数传导给输出响应，获得输出参数的概率分布特征。不确定性问题的主要计算方法包括摄动法[8]、蒙特卡洛法[9]、可靠性分析法[10]、响应面法[11]和谱分解方法[12]等等。谱分解方法在处理高斯分布和非高斯分布问题的计算效率方面有一定优势。为解决非高斯分布和参数协方差未知问题，广义多项式混沌方法（generalized polynomial chaos,GPC）成为当前研究热点。

本文将GPC 法应用于圆柱壳结构自由振动的不确定性分析，将自由振动不确定性研究范围从随机载荷不确定性方面扩展到考虑建造因素的不确定性问题。在文中建立自由振动不确定性分析模型，将结构建造因素中的不确定性传导并反映到圆柱壳结构自由振动特性概率密度分布。研究成果可用于考虑建造质量影响的舰艇结构声振特性的预报与控制。

1 广义多项式混沌方法

1.1 广义多项式混沌方法概述

在不确定性分析中，标准随机变量的选择将影响计算收敛性和截断项数，选择最佳匹配多项式可提高计算效率，如表1 所示。在声振特性不确定性计算中，采用Hermite 多项式拟合不确定性参数较为合适，其最高阶为3次。

表1 不确定参数对应的最佳多项式类型Tab.1 Uncertain parameter types and the corresponding orthogonal polynomials

1.2 广义多项式混沌方法的随机投影

选定多项式类型后，定义随机空间(Ω,γ,P)，其中Ω是总样本空间、γ是样本空间中的σ域、P是事件概率。对于随机空间，空间中任意不确定性变量χ可表示为

式中，Ψi为随机正交基，xi为待定系数。随机正交基Ψi是一组含有随机向量ξ的多项式，它们满足正交性条件：

1.3 广义多项式混沌方法的求解

应用广义多项式混沌方法，将结构中建造非确定性因素作为输入参数通过结构控制方程传递到输出的响应结果中，开展非高斯分布的随机问题求解。

应用GPC 法求解不确定性问题的步骤为：（1）将不确定性参数表示成多项式混沌展开式形式，求解该展开式系数；（2）用广义多项式混沌表达式表达不确定性输入参数和所求解响应结果；（3）将输入参数不确定性通过结构的随机控制方程传导至输出参数中，求得响应表达式中的未知系数。GPC法求解过程如图1所示。

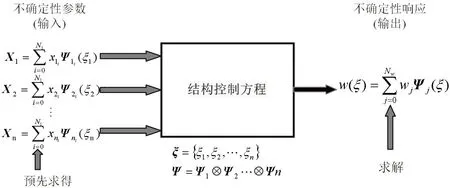
图1 基于GPC的求解过程示意图Fig.1 GPC-based solving flow chart

设结构声振方程满足线性条件，将图1所示的求解步骤应用于结构声振特性不确定性分析中，需获得结构中输入参数（如材料密度、板壳厚度、肋骨型号等）的概率密度分布。

通过不确定性传导功能，将结构参数不确定性特性传导至输出参数（即结构声振特性），获得结构声振特性概率密度分布，求解过程如图2所示。

图2 基于GPC的结构声振特性不确定性求解Fig.2 Dynamical solution based on GPC

2 不确定性输入参数

在应用GPC进行结构声振特性不确定性求解中，需求解式（4）中待定系数xi。设变量χ和ξ处于同一随机空间中且具有相同的概率分布，采用Galerkin投影法描述待定系数xi：

式中，a、b是标准随机变量上、下限。设式中χ(ξ)为未知函数，需进行随机空间转换以获得不确定性变量χ关于参数ξ的表达式χ=F(ξ)，变换方程如图3所示。

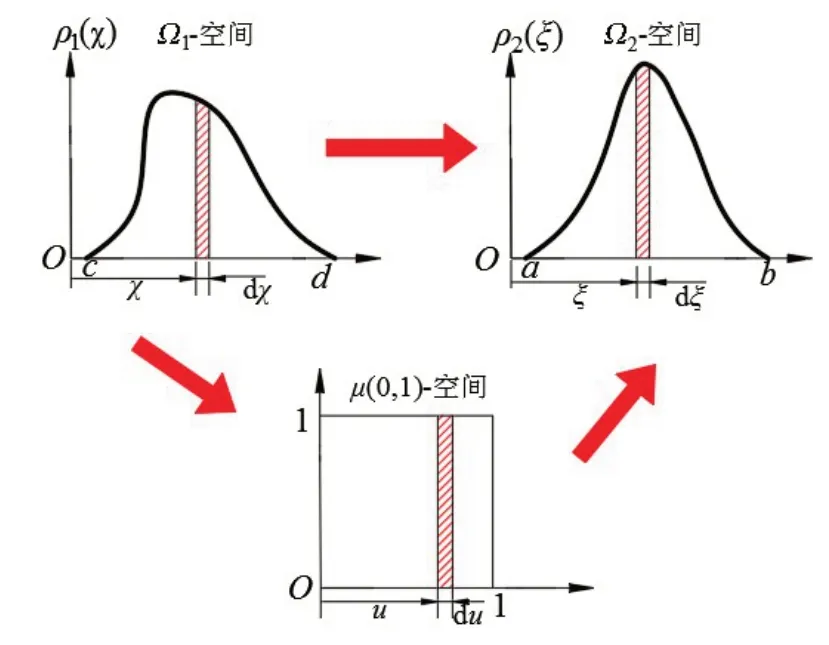
图3 不同随机分布之间的变换Fig.3 Conversion between uncertain parameters

在图3 中，不确定性变量χ在随机空间Ω1中，概率分布为ρ1(χ)，区间为[c,d]；随机参数ξ在随机空间Ω2中，概率分布为ρ2(ξ)，区间为[a,b]。不确定性变量χ和标准随机变量ξ间的变换满足：

对于大多数随机分布函数，式(7)中随机分布函数F(ξ)并不是一个显性表达式，需引入标准平均分布为中间变量实现对待定系数xi的转换方程，将式（7）代入式（6）中，可得

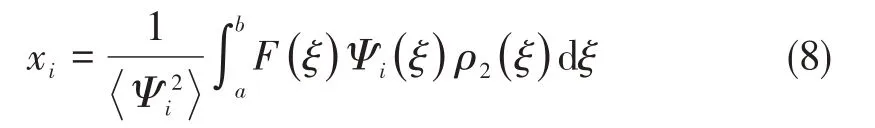
建立不确定性变量χ和标准随机变量ξ对于标准平均分布μ(0,1)的空间变换方程：

3 不确定性传导方程

3.1 不确定性传导

在结构声振特性不确定性分析中，研究输入参数不确定性对声振特性的影响，将输入参数（结构材料、结构几何尺寸等）的不确定性特性通过运动控制方程有效地传导到输出参数（结构响应、声学响应等）概率密度分布中。

在应用有限元法进行确定性固有频率系数λri分析中，涉及确定性刚度矩阵系数ki、确定性质量矩阵系数mi和确定性振型向量系数φri。由于涉及大量积分运算且非常耗时，需对传导方程进行改进。

3.2 配点法概述

对于大多数结构，其变量χ的概率密度分布ρ1(χ)无法通过明确的函数来表示，采用基于配点法（collection method，CM）结合试验数据获得ρ1(χ)的概率密度分布具有一定优势。配点法基本原理是基于最小二乘法原理，使两种预测结果间的误差达到最小，以确定相关的不确定性参数。

求解式（13），获得广义多项式混沌系数xi，进而获得χ的概率密度。配点法可直接避开通过式（8）中复杂积分运算求解系数的过程，减小计算复杂度和计算量。

3.3 配点法求解响应混沌系数

为提高计算效率，将配点法和广义多项式混沌法进行结合，用于作为输入参数的不确定性变量混沌系数及作为输出的结构响应表达式中混沌系数的求解，获得结构响应概率密度分布，其求解过程如图4所示。

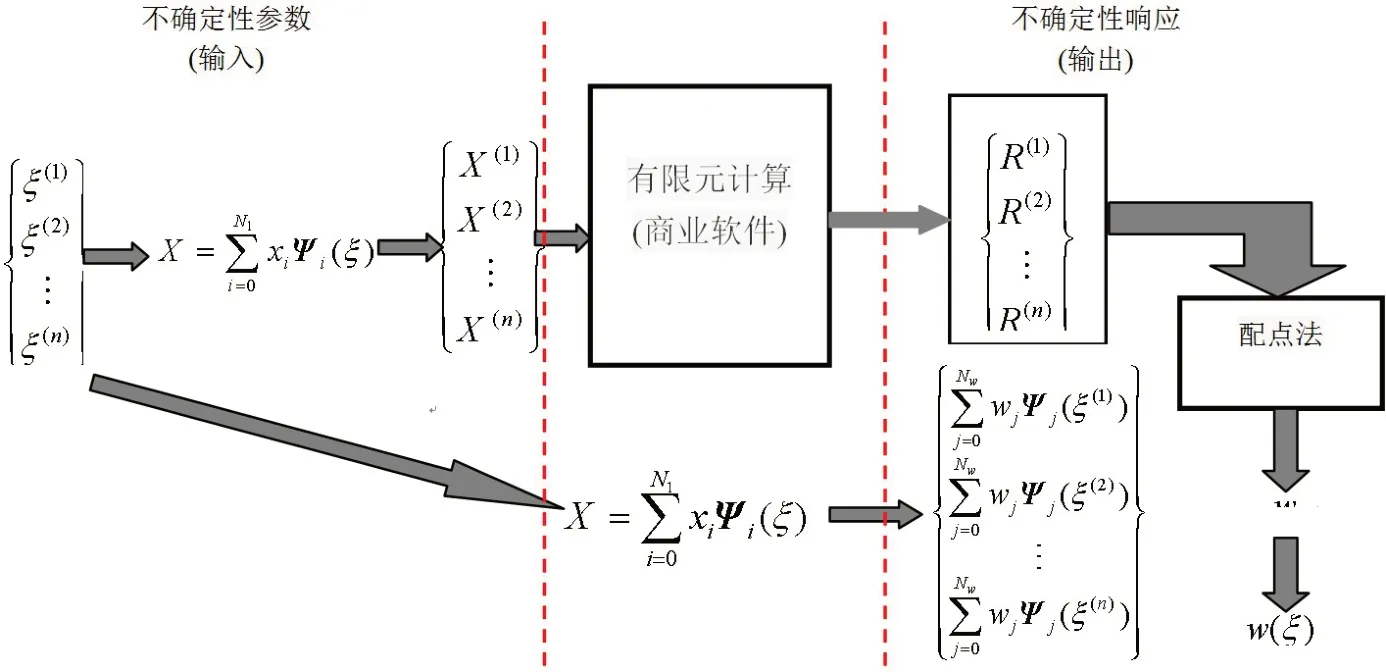
图4 配点法求解响应混沌系数Fig.4 Flow chart for obtaining response coefficients based on collocation method

从图4 可知，应用配点法结合GPC 法求解非确定性问题时，可避免应用确定性刚度矩阵系数、确定性质量矩阵系数、确定性振型向量系数求解确定性固有频率系数中的推导和计算。可直接利用成熟有限元商业软件进行求解，且可依托商业软件的计算优势简化计算过程，使计算效率最大化。

4 数值分析

4.1 模型概述

以圆柱壳模型为例，采用Galerkin 投影方法确定不确定性参数，分别采用GPC 法和蒙特卡洛法计算固有频率，验证GPC法的正确性。

具有两端简支圆柱壳结构的几何参数如表2所示。结构材料为钢，力学特性为：密度ρ=7860 kg/m3，弹性模量Em=2.1×1011Pa，泊松比μ=0.3。

表2 圆柱壳几何参数Tab.2 Cylindrical shell geometry parameters

4.2 弹性模量概率密度

弹性模量概率密度分布图如图5所示。

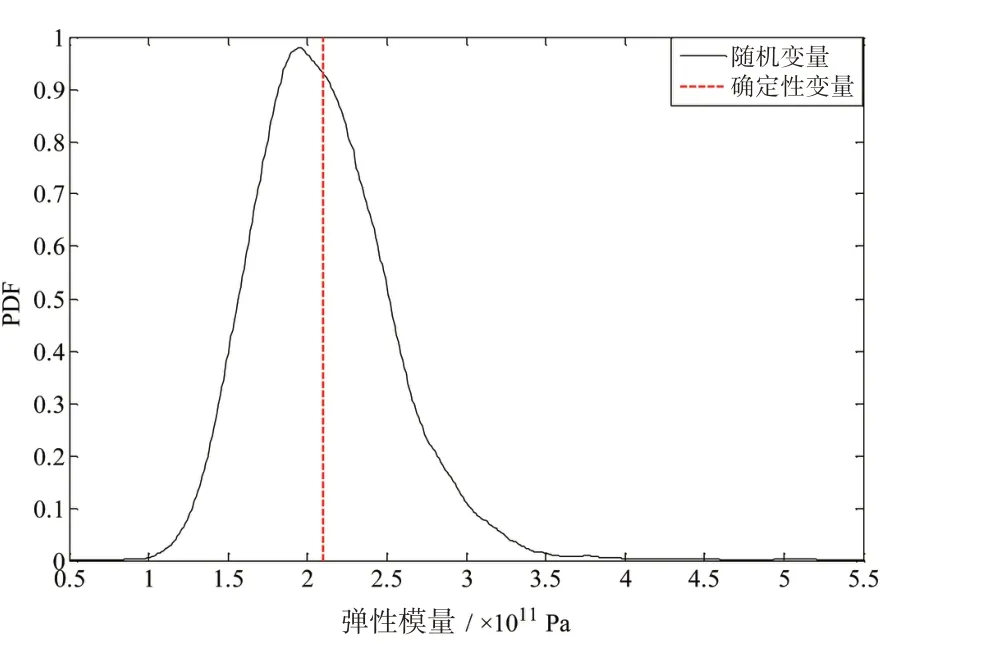
图5 弹性模量概率密度分布Fig.5 PDF of elastic moduli

4.3 固有频率概率计算

基于Hermite 多项式，结合GPC 法和配点法计算圆柱壳结构固有频率不确定性，计算步骤为：（1）定义圆柱壳结构几何参数、材料参数及弹性模量概率密度分布函数；（2）求解圆柱壳结构的确定性固有频率解；（3）将不确定性参数表示成多项式混沌展开式的形式；（4）推导含建造因素的圆柱壳结构自由振动方程；（5）引入随机变量，将建造不确定性参数定义为不确定性变量；（6）基于Hilbert 空间，引入正交基Ψi；（7）应用逆幂法（inverse power method）求解自由振动方程的特征值；（8）设定方程收敛标准，进行收敛性判断；（9）应用Galerkin投影法求解多项式混沌表达式中系数xi；（10）进行结构固有频率非确定性数值计算；（11）将计算结果与蒙特卡洛法进行对比。

图6 所示为用GPC 和不同模拟次数的蒙特卡洛法计算第一阶固有频率值对比，结构固有频率的变化满足正态分布。

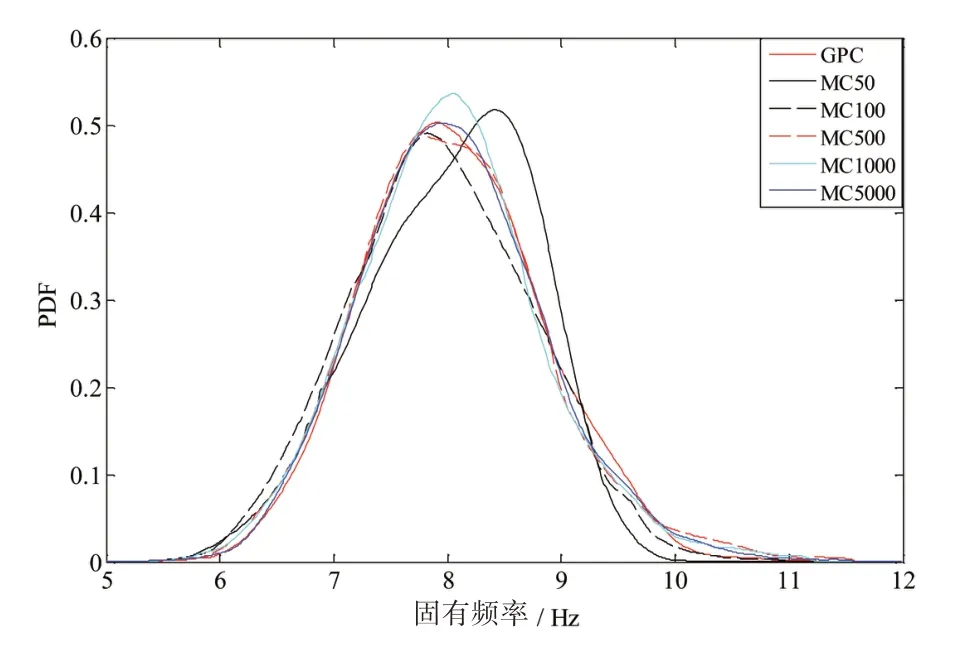
图6 GPC与蒙特卡洛法计算对比Fig.6 Comparison between GPC and different order MC

图7 分别为用GPC 法、5000 次模拟蒙特卡洛法计算的圆柱壳结构前4 阶固有频率的概率密度分布，图中竖直虚线表示为图5 中所定义的弹性模量期望值对应的固有频率。

由图7 可知，不同阶结构固有频率的变化满足正态分布。采用GPC 法计算结果同蒙特卡洛法计算结果具有较好的一致性，GPC 法在求解动力学问题方面的有效性得到了验证。

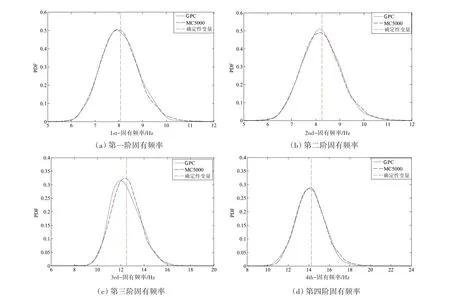
图7 GPC法同5000次模拟蒙特卡洛方法的固有频率对比Fig.7 Natural frequency comparison between GPC method and 5000 MC

4.4 计算效率验证

为验证GPC 法计算效率，对比GPC 法和不同模拟次数蒙特卡洛法的计算时间，如表3所示。

由表3 可知，在计算精度基本相似情况下，采用5000 次模拟蒙特卡洛法需137 247.6 s，而采用GPC 法仅需要184.2 s，计算时间远小于蒙特卡洛法。图7 和表3 表明，GPC 法在求解实际大型结构工程不确定性振动问题时具有明显的优势和潜力。

表3 GPC法同蒙特卡洛法的计算时间对比Tab.3 Consuming time of GPC and Monte Carlo

5 结 语

本文针对舰艇建造过程中的声振特性不确定性问题，推导了GPC 法对不确定性参数的求解公式及不确定性传导公式。以圆柱壳结构为例，将GPC 法与有限元数值方法相结合开展了结构动力学的非确定性分析。通过数值计算，验证了所提出方法的可行性和有效性。研究成果可应用于舰艇结构声振特性的精确预报，并可为舰艇声学质量控制提供策略。