横摇作用下气囊-浮筏耦合船用转子系统的非线性动力学特性
2022-08-17王军伟柳新科
谢 旋,李 明,王军伟,柳新科
(西安科技大学力学系,西安 710054)
0 引 言
船舶在海上航行时会受到强风、海浪等多种因素的影响,发生倾斜和摇摆运动,如横摇、纵摇和垂荡等[1]。在这些牵连运动中,横摇具有运动剧烈、周期短暂的特点,因此在研究牵连运动对船用旋转机械系统的影响时应予以重点考虑。虽然船体横摇频率远远低于气囊-浮筏耦合船用转子系统的工作频率,但是由横摇牵连运动产生的科式惯性力会直接影响到气囊-浮筏耦合船用转子系统的垂向和横向非线性动力学行为,因此研究横摇作用下的气囊-浮筏耦合船用转子系统的动力学特性具有重要意义。
气囊-浮筏隔振系统是一种性能优异的隔振设备,它可以通过充放气来调整各气囊的高度,并且具有固有频率低、承载能力大、驻波频率高和无蠕变等特点,被广泛应用于各种大型机械系统的振动控制。近年来,不少学者在浮筏隔振方面进行了研究,Li[2]建立了具有不同频率和不同幅值的多个激励作用下的浮筏系统的动力学模型,基于多尺度法求解幅频响应方程以及解的不稳定区域;Liu[3]研究了浮筏隔振系统(FRIS)对船用离心泵振动特性的影响;方媛媛[4]采用一种改进的Bingham 模型,推导了非线性磁流变阻尼力表达式,建立了船舶辅机浮筏隔振系统的动力学模型,分析了磁流变阻尼器各参数对隔振效果的影响规律;Zhao[5]考虑到基础激励源与浮筏隔振系统之间的耦合效应,建立了基础激励作用下系统的动力学模型,分析了系统的动力学特性。上述研究在气囊-浮筏耦合船用转子系统的动力学特性及浮筏隔振性能方面进行了比较深入的分析。
目前,关于牵连运动下转子-轴承系统动力学的研究工作主要集中在机载、车载和舰载等领域,例如,Hou[6-7]考虑了飞机悬停和正弦机动飞行两种工况,以不同工况下带有三次非线性弹性支承的转子系统为研究对象,建立方程进行理论、数值求解和分岔分析,详尽分析了机动转子系统的非线性动力学行为;Briend[8]考虑到汽车涡轮增压机和飞机涡轮机上机载转子的振动会受到各种支撑的影响,建立了多种支撑激励作用下机载转子的六自由度运动模型并分析了其动力学特性;Han[9-11]建立了包括旋转、俯仰和偏航运动下的柔性转子系统的动力学模型,分别对只含一个基本运动和两个运动耦合下的转子系统进行了分析,研究了多种参数激励对转子-轴承系统的稳定性的影响,提出并验证了基础纵摇运动作用下行星齿轮的动力学模型;Zhang[12-13]将基底运动和非线性油膜力耦合,研究了基础运动对长短轴承假设下非线性油膜力的影响,建立了考虑船舶横摇和纵摇运动作用下的船用涡轮机转子系统数学模型,分析了系统的非线性动力学行为;刘镇星等[14]考虑到舰船摇摆运动,引入非线性油膜力并利用拉格朗日方程建立了滑动轴承-齿轮副系统的非线性动力学模型以分析其动力学特性,为舰船设计中齿轮箱位置的布置提供参考依据;Han[15]建立了垂荡和非线性油膜力作用下的转子-轴承系统的动力学模型,研究了垂荡作用下船用转子系统的动力学行为。以上研究工作主要考虑了牵连运动对转子系统的影响。
动力系统的振动是船舶重要振动噪声源之一,为了保证舰船的安全性和隐蔽性,一般会采用气囊-浮筏作为隔振装置以实现船用动力系统的减振和降噪。船用旋转机械系统在增加了隔振装置后,由于受牵连运动的作用,船用转子—轴承系统的振动情况变得更为复杂,对隔振也提出了更高的要求,因此隔振系统的动力学行为研究及其参数优化显得非常迫切。本文重点研究横摇作用下气囊-浮筏耦合船用转子系统的非线性动力学特性。
1 横摇作用下系统的动力学模型
1.1 系统动力学方程的建立
横摇作用下气囊-浮筏耦合船用转子系统模型如图1 所示。为了更好地研究此问题,作以下假设:(1)只考虑船舶横摇的作用,船舶横摇时,始终绕着其旋转中心O1Z1轴转动,Z方向的运动应是一致的,q为船舶横摇角度,船舶平动的位移分别为x0、y0和z0,船舶平动加速度为0;(2)实际工况中气囊-浮筏耦合船用转子系统的安装位置到旋转中心有一定的距离,垂向距离用a、横向距离用b来表示,但为了计算简便,取a=0,b=0;(3)转子为刚性轴段,圆盘质量为m1,偏心距为e,转速为ω,转子相对于船的垂向位移和横向位移分别为x1和y1;(4)轴承为短轴承,在船舶横摇时轴承轴向(Z方向)的行为是一致的;(5)轴承支座及浮筏可看成一个整体,质量为m2,在船舶横摇过程中,轴承支座及浮筏整体相对于船的垂向位移和横向位移分别为x2和y2,气囊垂向、横向的刚度及阻尼都是线性的,气囊垂向总刚度为kv,横向总刚度为kh,气囊垂向总阻尼因子为cv,横向总阻尼因子为ch。O0X0Y0Z0是地面上的定坐标系,O1X1Y1Z1是船的平动坐标系,始终与定坐标系平行,O1X1′Y1′Z1′是固定在船上并随船旋转的坐标系,即联船坐标系[16]。
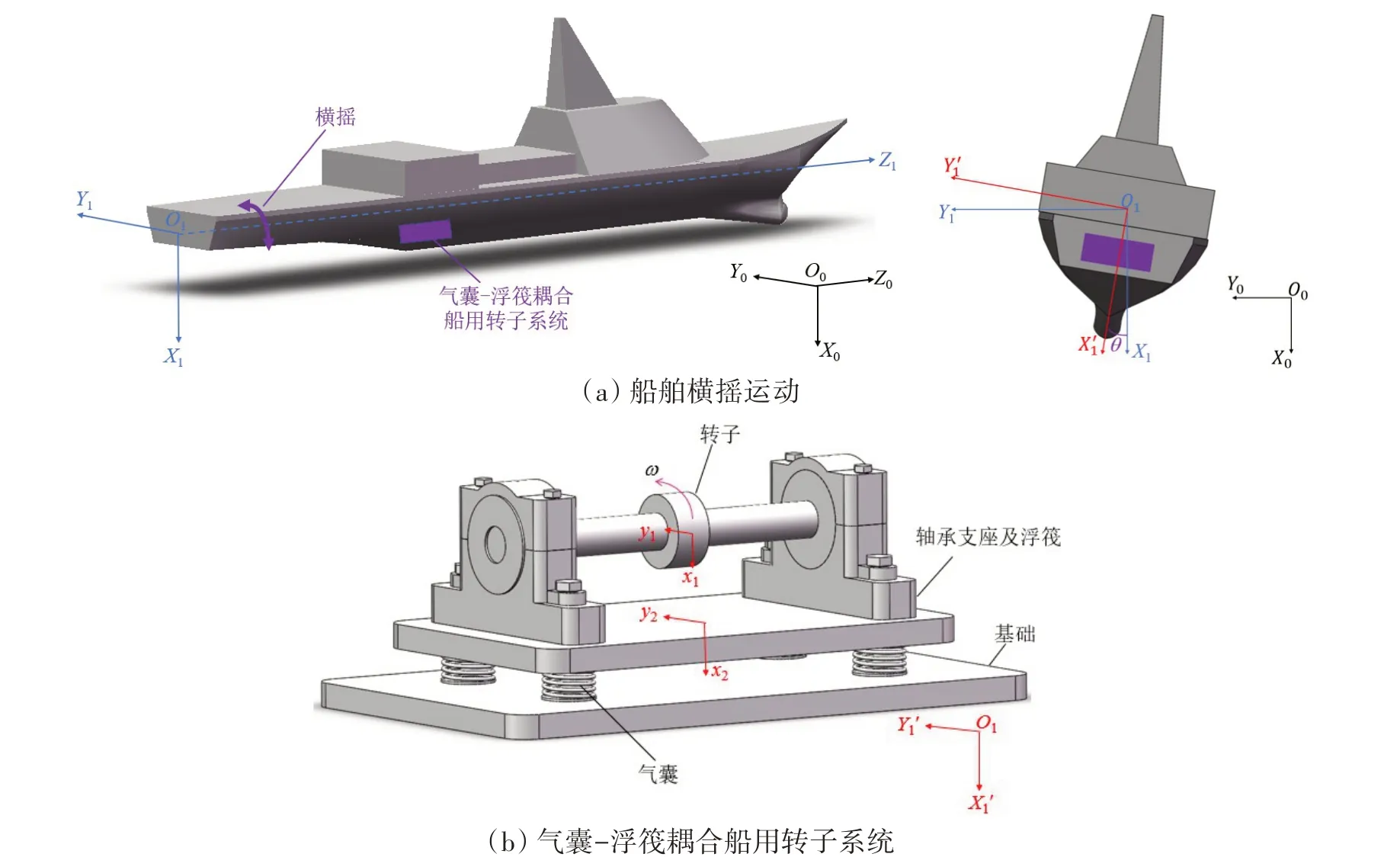
图1 船舶横摇运动和气囊-浮筏耦合船用转子系统示意图Fig.1 Schematic diagram of ship rolling motion and a marine rotor system coupled with air bag-floating raft
船舶横摇时,有坐标转换矩阵

以转子为研究对象,在定坐标系中的绝对位移为
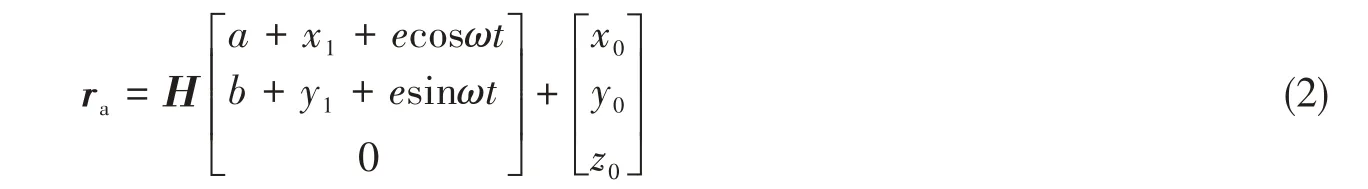
式中,横摇角度θ、转子相对于船位移x1和y1均与时间t有关。转子绝对位移ra对时间t求两次导数得到绝对加速度aa,根据假设(1),船舶平动无加速度,则绝对加速度为

式中,绝对加速度aa是由相对加速度项、牵连加速度项以及科式加速度项组成。由于转子只受重力和轴承油膜力,在定坐标系中有合力


1.2 无量纲方程
为了增强所研究内容的适用性,引入特征长度—轴承油膜间隙c、时间尺度—时间t等物理量,对动力学微分方程中的各个物理量进行无量纲处理,相关参数见表1。

表1 无量纲参数表达式Tab.1 Expression of dimentionless parameters
对方程进行无量纲化,有以下规定:ẋ=dx/dt,ẏ=dy/dt,θ̇=dθ/dt,X′=dX/dτ,Y′=dY/dτ以及θ′=dθ/dτ。假定船体产生横摇运动的横摇位移关系式满足正弦规律[13,20-21]θ=θmsin(ωz t),其中,θm是无量纲横摇幅值,ωz是横摇频率。又由τ=ωt,可以把θ表示成关于无量纲时间τ的函数:

对式(8)进行无量纲化,并与式(11)联立得到系统无量纲运动方程:

式中,Ω是转子无量纲转速,η是转子无量纲转速与无量纲横摇频率之比,α是转子无量纲偏心距,θm是无量纲横摇幅值,n是质量比,Ωvn和Ωhn分别是轴承支座及气囊浮筏整体的无量纲垂向、横向固有频率,fx和fy为无量纲非线性油膜力。
对式(9)无量纲化,得非线性油膜力的无量纲表达式:
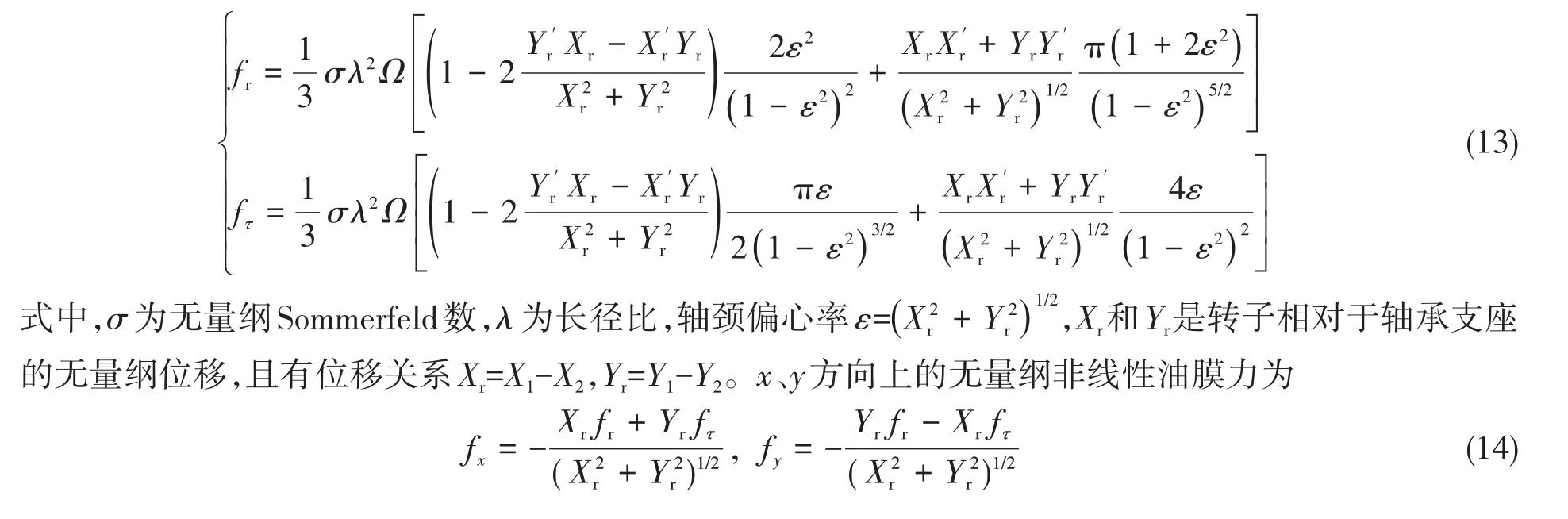
2 非线性动力学分析
考虑到油膜力的强非线性特性,采用4 阶Runge-Kutta 方法对无量纲的动力学微分方程进行求解。气囊浮筏-耦合转子系统无量纲参数取值:σ=3、λ=0.2、α=0.05、n=60、Ωvn=0.5、Ωhn=0.5、ζv=0.1及ζh=0.1,转子转速W取值范围为0.6~3.5。船舶发生横摇时,主要参数有幅值和频率,参数取值范围[22]见表2。

表2 船舶横摇参数取值范围Tab.2 Range of ship rolling parameters
2.1 转子转速变化对横摇作用下系统动力学特性的影响
图2(a)为横摇幅值θm=0 时,即无横摇作用时系统位移随转子转速Ω变化的分岔图。系统随转子转速的增加表现出周期1、周期2、准周期和混沌等典型的非线性动力学特性,具体表现为:转速小于2.29时,系统呈稳定的周期1运动状态;随着转速的增加,系统运动状态由周期1经倍周期分岔到周期2;转速继续增加,系统运动状态由周期2 分岔的两支合为一支,系统呈周期1 运动状态;转速持续增加,系统发生准周期分岔,转子的位移幅值也在持续增大,系统呈准周期运动状态;转速持续增加至大于3.43后,最大Lyapunov指数数值大于0,系统处于混沌状态。

图2 位移Xr随转速Ω变化的分岔图及最大Lyapunov指数Fig.2 Bifurcation diagram of displacement Xr with speed Ω and its largest Lyapunov exponents
图2(b)为横摇幅值θm=0.05、横摇频率Ωz=0.01时,横摇作用时系统位移随转子转速Ω变化的分岔图。横摇作用下的转子系统随着转子转速增加表现出准周期和混沌的非线性动力学特性,表现为:转速较低时,系统处于准周期运动状态;转速增加至2.29处,准周期由一支分岔为两支,系统运动状态仍是准周期的;转速继续增加至2.61处,准周期分岔的两支又合为一支,系统处于准周期运动状态;转速持续增加,系统位移幅值也持续增加,随后转速增加至3.43 处,最大Lyapunov 指数数值大于0,系统进入混沌状态。与无横摇作用的系统相比,横摇作用下系统的运动状态更为复杂。
图3~6是横摇幅值θm=0.05、横摇频率Ωz=0.01时,转子转速Ω分别为1.11、2.57、2.82和3.48情况下系统的动力学稳态响应。转子转速Ω=1.11时,转子轴心轨迹形似“梭形”,对比垂向和横向位移变化,横向的振动幅值更大,庞加莱截面上的点构成了一条封闭曲线;时域响应中转子位移峰值随着时间的波动较小,频域响应中横摇频率f0和工作频率f1=1/2π=0.159 占主要成分,倍频2f1等存在但占比很小,此时最大Lyapunov指数为-0.027 71,系统处于准周期运动状态。

图3 θm=0.05、Ωz=0.01、Ω=1.11时,系统的稳态响应Fig.3 Steady-state response of the system with θm=0.05,Ωz=0.01,Ω=1.11
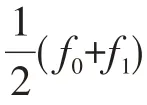


图4 θm=0.05、Ωz=0.01、Ω=2.57时,系统的稳态响应Fig.4 Steady-state response of the system with θm=0.05,Ωz=0.01,Ω=2.57
转子转速Ω=2.82时,系统的稳态响应较之前更为平稳,振动幅值减小并趋于稳定。这时轴心轨迹图中转子的垂向和横向位移变化对比,转子垂向振动幅值略大于横向,庞加莱截面上的点构成了一条封闭曲线;时域响应中位移峰值的波动较小,频域响应中横摇频率f0和工作频率f1=1/2π=0.159占主要成分,还有倍频2f1等存在但占比很小,此时最大Lyapunov指数为-0.008 46,系统处于准周期运动状态。
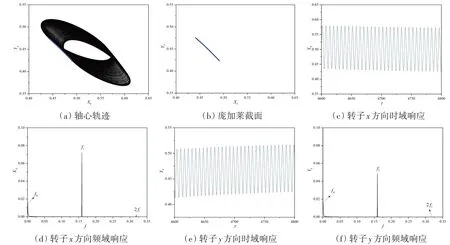
图5 θm=0.05、Ωz=0.01、Ω=2.82时,系统的稳态响应Fig.5 Steady-state response of the system with θm=0.05,Ωz=0.01,Ω=2.82



图6 θm=0.05、Ωz=0.01、Ω=3.48时,系统的稳态响应Fig.6 Steady-state response of the system with θm=0.05,Ωz=0.01,Ω=3.48
图7 为有无横摇作用下转子垂向、横向振动幅值与转子转速关系。这时横摇作用的幅值θm=0.05,对比无横摇作用的系统,有横摇作用的系统垂向、横向振动幅值都更大。转子转速Ω从0.6 至1.11,振动幅值呈增加趋势;Ω从1.11 至2.3,振动幅值有所减小;Ω从2.3 至2.6,振动幅值突然增加后又减小;Ω从2.6 至3.08,振动幅值稍有增加趋势;Ω大于3.08 后,振动幅值增加迅速。低转速时,转子横向振动幅值大于垂向;高转速时,转子垂向振动幅值大于横向。

图7 转子振动幅值与转速关系Fig.7 Relationship of rotor vibration amplitudes with speeds
2.2 横摇幅值对系统动力学特性的影响
图8为横摇频率Ωz=0.01,横摇幅值θm分别等于0.25、0.45时系统的分岔图及其最大Lyapunov指数图。对比图2中无横摇作用和横摇幅值θm=0.05时系统的分岔图及其最大Lyapunov 指数图,在较大横摇幅值的情况下,随着转子转速增加,系统仍是在固定的转速时发生分岔、并以一确定的转速进入混沌,由此可见,横摇幅值的变化并不会影响到系统运动状态的改变。

图8 不同横摇幅值时位移Xr随转速Ω变化的分岔图及最大Lyapunov指数Fig.8 Bifurcation diagram of displacement Xr varying with speed Ω and its largest Lyapunov exponents at different roll amplitudes
图9为不同横摇幅值条件下转子垂向振动幅值与转速的关系。不同横摇幅值下的转子垂向振动幅值随转速变化的曲线具有相似性。在转速变化范围内,大横摇幅值对应的曲线始终在小横摇幅值对应的曲线的上方,说明横摇幅值的增加会使系统的振动幅值增大。
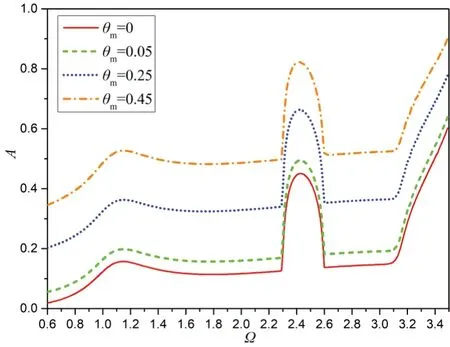
图9 不同横摇幅值时垂向振动幅值与转子转速关系Fig.9 Relationship between vertical vibration amplitude and rotor speed at different roll amplitudes
图10 为不同的转子转速条件下转子的垂向振动幅值随横摇幅值的变化关系图。随着横摇幅值的增加,垂向振动幅值以曲线的形式增大;在转速Ω=3.48 条件下,横摇幅值增加到0.64 时,转子垂向振动幅值为1,垂向振动幅值等于轴承油膜间隙,转子与轴承发生碰撞,大角度的横摇对高转速转子系统运行的安全稳定性影响极大;对比图中转速Ω=2.57和Ω=2.82时垂向振动幅值与横摇幅值的关系曲线,θm小于0.5 时,两条关系曲线几近重合,θm大于0.5 后,Ω=2.57 对应曲线始终在Ω=2.82 对应曲线的上方,系统在转速为2.82时抵抗大幅度横摇的能力较转速为2.57时更强。
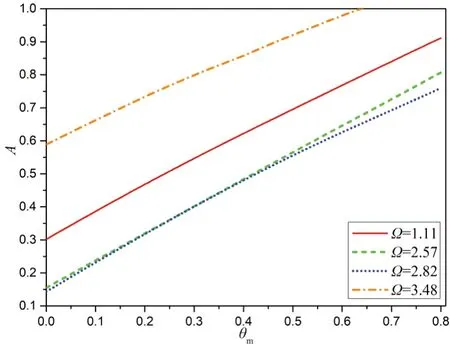
图10 不同转子转速时垂向振动幅值与横摇幅值关系Fig.10 Relationship between vertical vibration amplitude and roll amplitude at different rotor speeds
3 结 论
在对横摇作用下气囊-浮筏耦合船用转子系统的非线性动力学特性进行研究时,本文考虑了船舶横摇运动对气囊浮筏耦合船用转子系统的影响,建立了横摇作用下系统的动力学模型,对动力学方程进行了无量纲化处理,并采用数值方法求解得到了系统的稳态响应,分析了横摇作用下系统的非线性动力学特性。研究表明:
(1)横摇作用下气囊-浮筏耦合船用转子系统的运动状态,随转子转速的增加表现为:准周期→混沌;相较于无横摇作用的系统出现的周期1、周期2等简单周期同步运动,横摇作用下系统的运动状态更为复杂;对比无横摇作用时系统的振动幅值,横摇作用下系统的振动幅值增大明显。
(2)横摇作用下气囊-浮筏耦合船用转子系统,随着横摇幅值的增大,其运动状态仍是由准周期过渡到混沌,一般情况下横摇幅值的增减不会影响到横摇作用下系统的分岔及混沌特性。此外,横摇作用下系统的振动幅值会随着横摇幅值的增大而增大,且这种增大关系是以曲线形式呈现的。
