考虑斜置弹簧阻尼的船舶轴系纵振高静低动隔振器的建模研究
2022-08-17杨志荣李林桃饶柱石
杨志荣,李林桃,赵 含,饶柱石
(1.集美大学 轮机工程学院,福建 厦门 361021;2.厦门市海洋腐蚀与智能防护材料重点实验室,福建 厦门 361021;3.上海交通大学 机械系统与振动国家重点实验室,上海 200240)
0 引 言
由螺旋桨非定常激励力引起的推进轴系纵向低频振动对舰艇声隐身性能的危害性受到国内外学者的广泛关注[1-3]。对于舰艇推进轴系而言,其纵向振动控制的研究重点是减小经推力轴承基座传递至艇体的二次脉动激励力。由于纵向力传递路径为螺旋桨-传动轴-推力轴承-推力轴承基座-艇体,因此只能在此路径上对振源进行隔离或者消减。实际工况中,推进轴系的纵向静推力一般较大,隔振器需承受较大的静载荷,轴系蹿动位移的限制使得隔振器刚度不能过低,这就导致系统整体固有频率比较高,面对低频激励无法有效隔振。高静低动隔振器通过并联正、负刚度机构,可以获得高静刚度、低动刚度的特性,具有良好的低频隔振效果。Carrella 等[4]基于三弹簧并联的准零刚度结构,比较分析了三种初始状态下的斜置弹簧对系统隔振效果的影响;刘兴天[5]讨论了由滑动梁与线性弹簧组成的准零刚度系统带来的新特性;徐道临[6]等设计并分析了一种具有准零刚度的磁力隔振器,该隔振器同时具有磁力刚度非线性与几何结构非线性;Sun等[7]利用剪刀式结构本身的特性,使得线性的弹簧阻尼元件发挥出非线性刚度和阻尼的效果;Liu等[8]则将剪刀式结构与杠杆结构相结合,利用结构自身内在的非线性实现超低频隔振;周加喜等[9]利用高静低动结构,设计出一种分段准零刚度隔振器,避免了激励幅值过大所导致的共振峰值传递率超过等效线性系统峰值传递率。
然而,上述高静低动隔振器均是将隔振载体当作刚体,而在螺旋桨叶频激励力下,推进轴系自身的分布刚度不可忽视,同时大部分的高静低动隔振器的阻尼考虑为线性阻尼,较少考虑具有非线性阻尼作用下高静低动隔振器的隔振特性。本文针对在推进轴系上安装带连杆弹簧并联结构的高静低动隔振装置,考虑斜置弹簧阻尼情况,利用有限元法建立推进轴系-高静低动隔振器纵振隔振系统的动力学模型,分析其在特定参数下隔振器的隔振效果。
1 高静低动隔振器力学模型
对于如图1 所示的连杆-弹簧式的高静低动隔振器,其在承载物重力作用下处于静力平衡状态,且长度为b的连杆朝向水平。此时,竖直弹簧刚度为kv,预压缩变形量为δv;斜置弹簧刚度为kh,原长为Lho,数量为N组,隔振平台至水平弹簧固定端的距离为a,且满足a>b,此时有

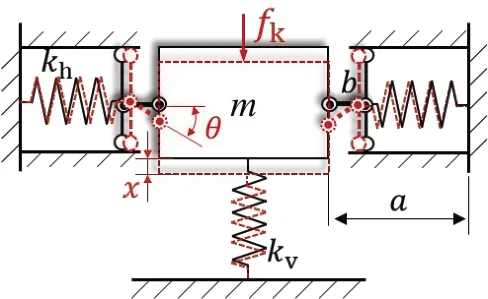
图1 带连杆-弹簧高静低动隔振器Fig.1 Rod-spring typed HSLDs vibration isolator
若此时给该隔振平台一个竖直方向的扰动x,则连杆做旋转运动,并与水平方向产生θ夹角。对于该扰动,产生相应的竖直方向回复力为
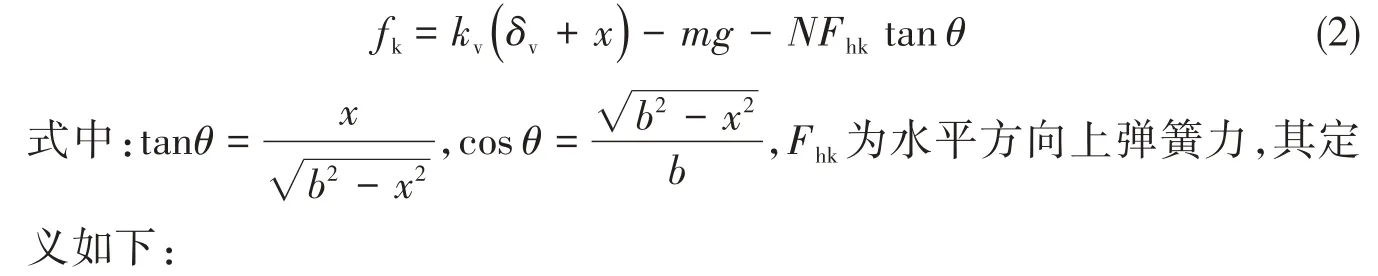

结合式(2)~(3),得

此回复力是仅考虑刚度作用时的整个系统的回复力。将式(4)在x=0处进行泰勒展开,并省略高阶项可得
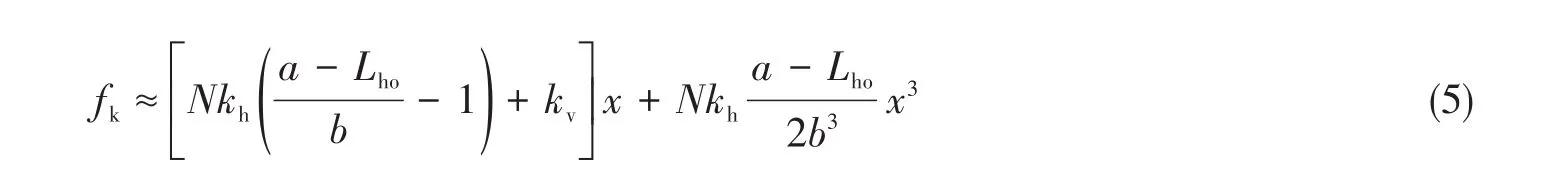
因此,可得近似后的高静低动隔振器的一阶刚度和三阶刚度分别为

2 推进轴系-高静低动隔振器动力学建模
2.1 考虑隔振器为轴向粘性阻尼时的纵振动力学建模
推进轴系主要由螺旋桨、艉轴、中间轴、推力轴、艉轴承、中间轴承和推力轴承等组成。这里将螺旋桨及其附连水质量简化为集中质量mp,推进轴等效为一根直径为d的弹性等截面均质轴,且只考虑纵向激励,忽略弯矩对纵向振动的影响。在推进轴系的推力轴承端配置连杆-弹簧高静低动隔振器,推力由螺旋桨经推力轴传递至该隔振器,再导入到推力轴承上,其系统动力学简化模型如图2 所示,其中轴的横截面面积、弹性模量、长度、以及密度分别用A、E、L和ρ来表示。

图2 推进轴系-高静低动隔振器力学模型Fig.2 Schematic diagram of the propulsion shafting-HSLDs
高静低动隔振器的回复力取如式(5)中的前四阶泰勒展开式,k1和k3分别表示式(6)~(7)中隔振器的一阶刚度和三阶刚度。此外,在图1隔振器的竖直方向上并联阻尼系数为cv的线性阻尼器,则图2中轴系推力轴承端的纵向阻尼系数为

针对该推进轴系-高静低动隔振器系统动力学模型,利用有限元法进行分析。将推进轴系模型划分为图2中的n个单元,即n+1个结点,则系统的动力学微分方程可以写为
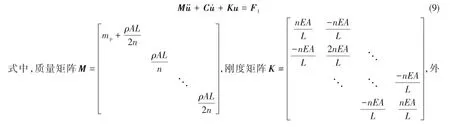

2.2 考虑隔振器斜置弹簧阻尼的纵振动力学建模
一般情况下,高静低动隔振器仅考虑竖直方向上线性阻尼的影响,而在水平方向上配置线性阻尼器时,特殊的几何布置结构会导致竖直方向上的非线性阻尼效果。为了研究此类阻尼的可控性,在图1 所示的原始高静低动隔振器模型基础上,分别给斜置弹簧和竖直弹簧并联一个线性阻尼器,其结构如图3所示。故本节分析配置如图3所示的带斜置阻尼的高静低动刚度隔振器的轴系纵向力学传递特性变化,其中,cv为竖直方向阻尼,ch为斜置阻尼,因此,图2中的c不再是常数,而是关于cv、ch以及轴系纵向位移的变量。
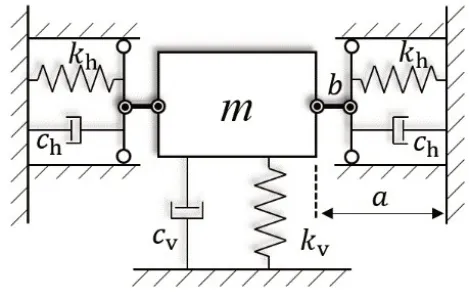
图3 配置阻尼的连杆-弹簧高静低动隔振器Fig.3 Rod-spring typed HSLDs vibration isolator with dampers
考虑斜置的阻尼器为粘性阻尼,在竖直方向产生大小为x的位移时,则水平方向上的阻尼力模型可以写为
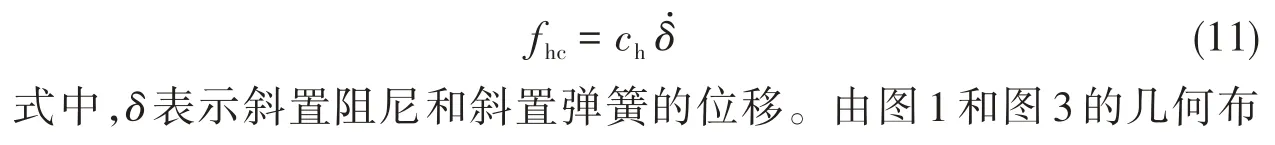


2.3 算例分析
根据上述建立起的系统动力学方程,仿真分析本文提出的非线性隔振器在推进轴系上的隔振效果。由于本文选择的有限元法需要进行网格无关性检验,分别计算推进轴系在等效线性隔振系统下(k1=kv,k3=0,ζh=0,ζv=0.01,kv=108N/m),单元数量选择5、10 和40 时的力传递率曲线,其它的结构参数参考某船轴系进行简化选取,如表1 所示。不同单元数量下的力传递率曲线如图4 所示,由图可知,10 至60 单元计算模型的第一、二阶纵向共振峰基本重合。因此为了保证计算的精度以及避免不必要的计算负担,本文的推进轴系计算模型选择10单元的有限元模型。此外,为了验证本文利用谐波平衡法所得近似解析解的准确性,将龙格库塔法求解式(19)得到的数值解作为精确解与之进行对比,此时,同时考虑非线性刚度和非线性阻尼的效果,参数选择N=2,ζh=0.01,ζv=0.05,kv=109N/m,其它参数按表1 进行选取,计算结果如图5 所示。由图可知,近似解析解与数值解在低频处存在着误差,但整体上基本吻合。
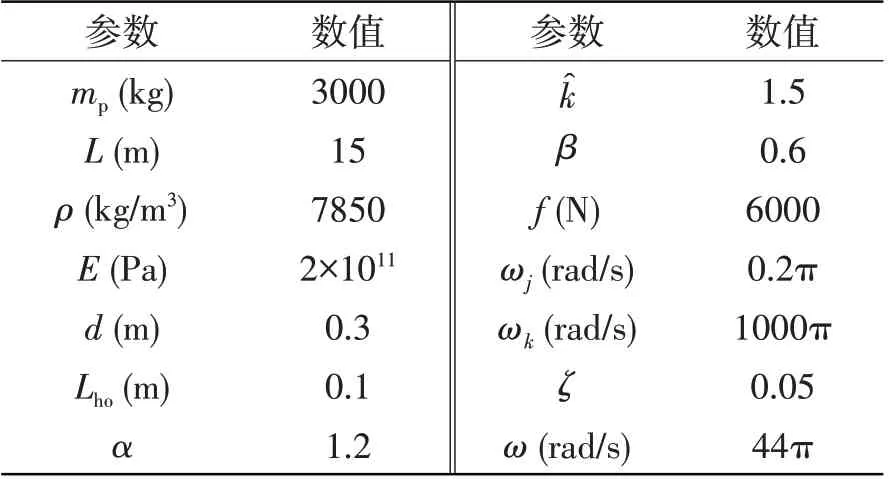
表1 推进轴系系统参数Tab.1 Parameters of propulsion shafting
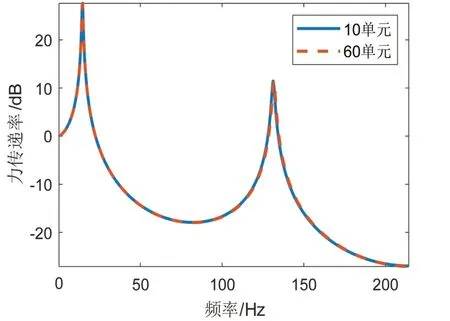
图4 不同单元数等效线性隔振系统有限元模型的力传递率曲线Fig.4 Force transmissibility curves of finite element models of equivalent linear vibration isolation system with different number of elements
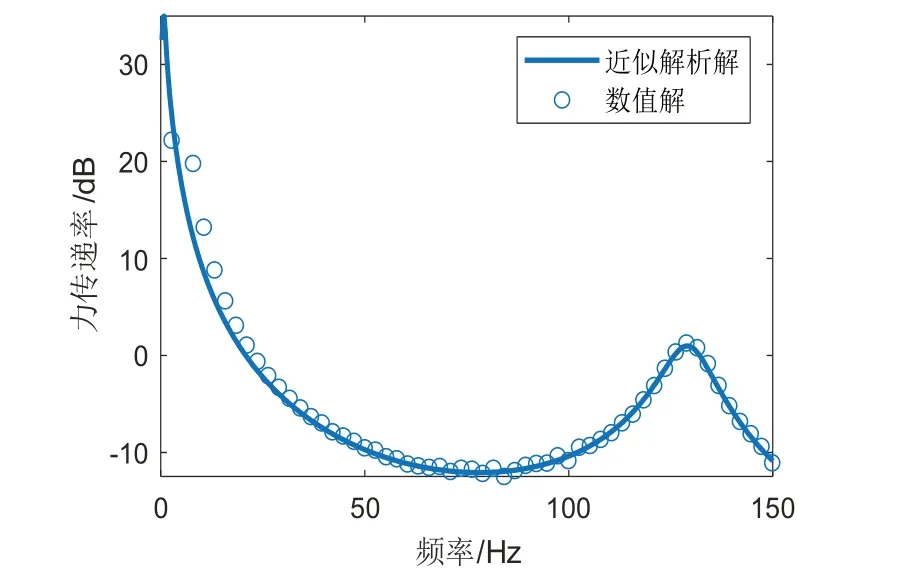
图5 非线性隔振系统力传递率曲线的近似解析解与数值解Fig.5 Approximate analytical solution and numerical solution of force transmissibility curves of nonlinear vibration isolation system
分别计算推进轴系在等效线性隔振系统下和推进轴系带高静低动隔振器隔振系统下的力传递率。系统中存在三种阻尼:推进轴系材料粘性阻尼比ζ、高静低动隔振器轴向阻尼比ζv和高静低动隔振器横向阻尼比ζh。首先对于线性系统,分析ζ与ζv对系统的影响,图6~7为当kv=1×109N/m,不同ζ与ζv取值时,线性隔振系统的力传递率及轴系在推力轴承端的结点位移幅值。图8~9为当kv=1×108N/m,不同ζ与ζv取值时,线性隔振系统的力传递率及推力轴承端结点位移幅值。
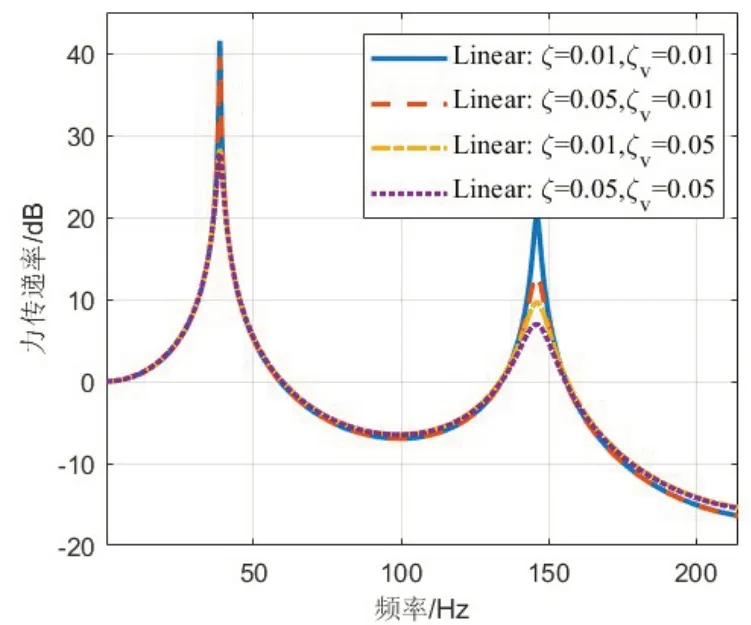
图6 不同ζ与ζv取值时线性隔振系统的力传递率(kv=1×109 N/m)Fig.6 Force transmissibility curves of linear system with different ζ and ζv(kv=1×109 N/m)

图7 不同ζ与ζv取值时推力轴承端的位移幅值(kv=1×109 N/m)Fig.7 Displacement curves of linear system with different ζ and ζv(kv=1×109 N/m)
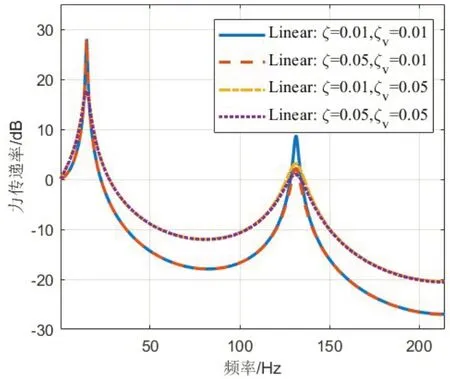
图8 不同ζ与ζv取值时线性隔振系统的力传递率(kv=1×108 N/m)Fig.8 Force transmissibility curves of linear system with different ζ and ζv(kv=1×108 N/m)
由下图可知,随着材料阻尼比ζ的增加,幅频响应的各阶共振峰均会下降,同样随着高静低动轴向阻尼ζv的增加,幅频响应的各阶共振峰也均会下降,即高静低动轴向阻尼ζv对共振响应幅值的抑制更为强烈。对于力传递率而言,增加ζ和ζv都会使得共振峰值下降,其中,增加ζ,对于非共振区域没有影响,而增加ζv会增加非共振区域的力传递率。此外,当ζv下降时,也使得ζv和ζ对共振峰抑制的强烈程度发生改变。进一步分析安装高静低动隔振器的船舶推进轴系系统受阻尼的影响,其中kv=1×108N/m,其他参数取值由表1给出。由图10可知,考虑斜置弹簧阻尼的高静低动隔振器非线性隔振系统在低频段的力传递率均下降,低频隔振效果更好,但是高静低动隔振器的轴向阻尼比ζv越大,在高频段隔振系统的隔振效果越差。对于线性系统,增加ζv会增加非共振区域的力传递率。由图11可以发现,高静低动隔振器低频的响应位移均增大,对于第一个共振峰,增加高静低动轴向阻尼比ζv可以有效地降低响应峰值,而改变高静低动隔振器横向阻尼比ζh,则无明显效果。除此之外,增加ζh可以使得系统的低频响应降低。
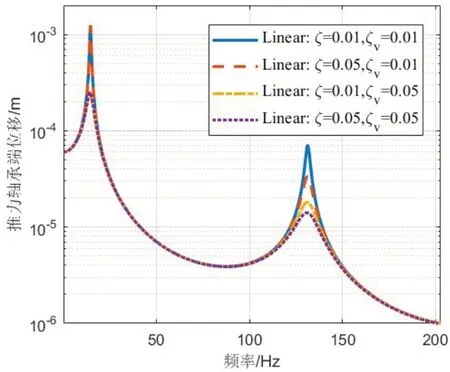
图9 不同ζ与ζv取值时推力轴承端的位移幅值(kv=1×108 N/m)Fig.9 Displacement curves of linear system with different ζ and ζv(kv=1×108 N/m)
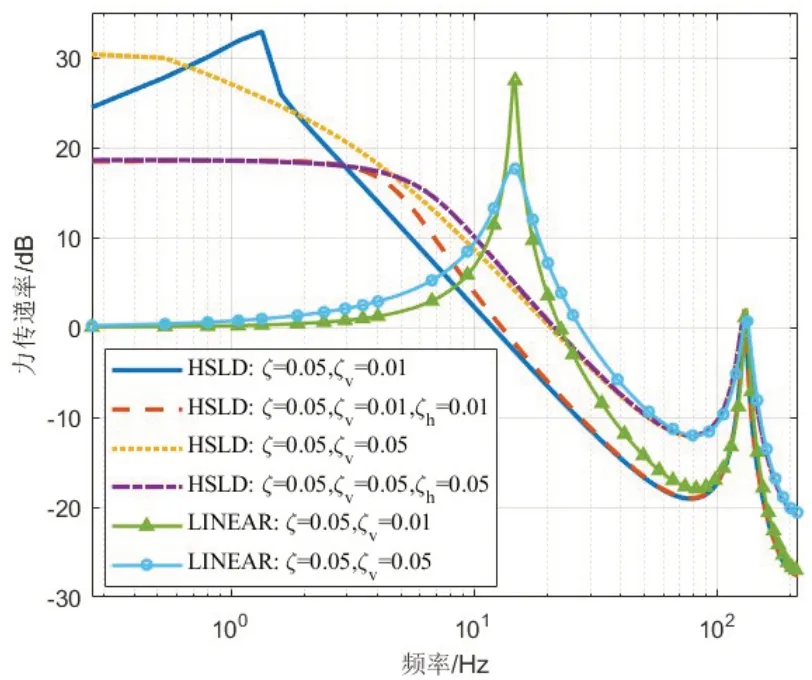
图10 不同ζ与ζv取值时非线性隔振系统的力传递率Fig.10 Force transmissibility curves of linear system with different ζ and ζv
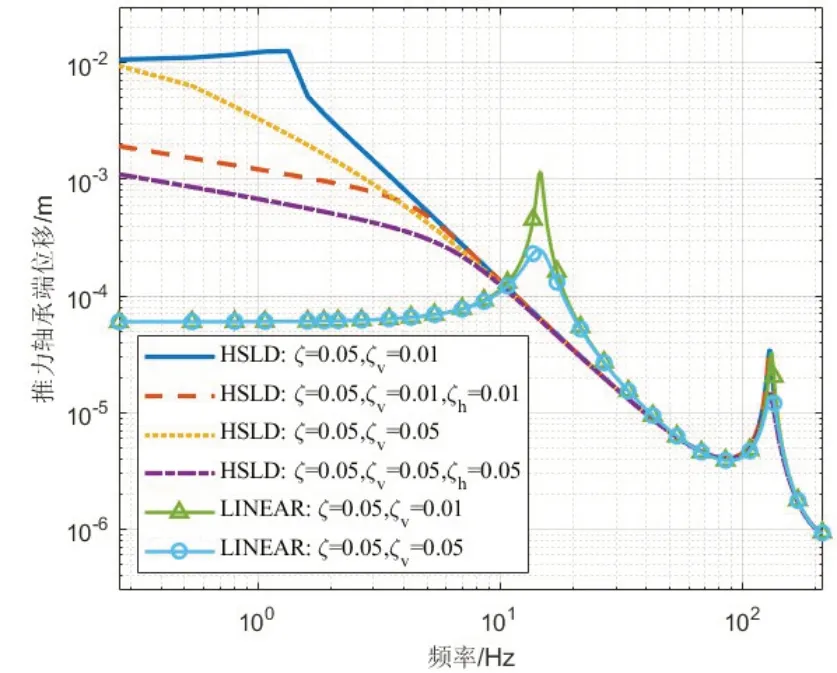
图11 不同ζ与ζv取值时推力轴承端的位移幅值Fig.11 Displacement curves of linear system with different ζ and ζv
3 结 论
本文针对推进轴系上安装的带连杆-弹簧并联结构的高静低动隔振装置,考虑斜置弹簧阻尼情况,利用有限元法建立了推进轴系-高静低动隔振器纵振隔振系统的动力学模型,分析其在特定参数下隔振器的隔振效果,通过分析可以得出以下结论:
(1)建立的考虑推进轴系自身分布刚度和斜置弹簧阻尼作用下的推进轴系-高静低动隔振器系统的非线性动力学模型更为精确;
(2)对于等效线性隔振系统,增加ζ和ζv都会使共振峰值下降,其中,增加ζ,对于非共振区域没有影响,而增加ζv会增加非共振区域的力传递率;
(3)考虑斜置弹簧阻尼的高静低动隔振器隔振系统的低频隔振效果更好,此外,随着高静低动隔振器的轴向阻尼ζv变大,在高频段隔振效果变差。
