基于最大化能效的海上中继通信频谱分配算法

孙 林, 毛忠阳,*, 康家方, 张 磊

(1. 海军航空大学航空通信教研室, 山东 烟台 264001;2. 海军航空大学信号与信息处理山东省重点实验室, 山东 烟台 264001)

0 引 言

在相距过远时,无人艇之间可能会由于传播损耗而出现通信中断,无法维持正常的通信。多跳中继传输技术可以较好地解决这一问题。多跳中继传输与传统单跳传输相比,具有延伸覆盖范围广的优点,可用于降低通信中断的发生概率。此外,由于携带能量有限,无人艇还需考虑如何高效利用能量,从而延长工作时间。多跳中继同时还具有低系统发射功率优点,正好契合节点节约能量的需求。因此,为满足无人艇在中继通信时,降低中断发生概率、合理利用有限能量的目的,需对海上多跳中继通信的频谱分配策略开展研究。

文献[1]提出了一种基于多跳中继的异构超密集网络联合功率分配和中继选择算法,采用了低计算复杂度的迭代注水算法,该算法首先运行集合中的充水过程,生成水位和功率分配向量。然后提取负的分配功率给集合,并在新的集合中重复这个过程,直到不需要负的元素来提取集合。通过这个迭代过程,集合中的水位将收敛到相等的水位,并获得最佳的功率分配。文献[2]针对静态信道分配问题,提出了一种启发式算法来解决优化问题。通过为通信链路分配信道来解决该问题,以最小化整个网络的干扰。针对该问题,提出了一种改进的粒子群优化算法,并采用一种新的合并方法为违反无线约束的节点重新分配信道。文献[3]提出了以最小频谱效率为约束条件的能量效率优化问题。对于能量效率优化问题,通过将目标函数的分子表示为凹函数的差,并利用参数变换,将非凸优化问题转化为凸优化问题。上述文献对商用框架下中继网络的频谱和功率分配做了研究。然而,由无人艇构成的多跳中继链路与上述文献中的多跳中继链路有不同之处。在无人艇链路组成的链路中,没有大型基站或网络骨干节点参与,甚至可能会缺少中心控制节点。并且，由于节点频繁的运动,链路的不确定性大大增加。针对这种情况,研究一种分布式频谱资源分配策略十分必要。文献[4]研究了由无人机构成的网络实时中继分配和频谱分配的策略。文献[5]通过考虑基于双向全双工的放大转发中继的机会选择,分析了底层认知网络中二次用户的性能,推导了各种性能指标的理论闭式表达式。这些都对研究分布式频谱资源分配策略提供了参考意义。

研究分布式频谱资源分配策略,需要对节点间通信中断进行分析。文献[6]对部署中继的最佳数量及位置展开研究,以达到最小化整条链路中断概率的目的。文献[7]通过评估第个中继的中断概率累积分布函数,以封闭形式获得了基于放大转发协议多跳中继网络的中断概率。文献[8-9]提出一种基于解码转发协议的逐跳中继选择策略,在最大发射功率和最大干扰约束下,对中断概率进行了分析。文献[10]对分级海事无线电网络,在确定船舶的QoS需求后,通过数据速率阈值反推得到了中断概率函数并进行分析。上述文献都是从整条链路的角度对总的中断概率进行分析,进而确定频谱分配策略。这是因为基于节点能够掌握整条链路的路由信息。但在由无人艇构成的链路中,路由信息可能会由于节点运动而频繁更改,仍然采用基于节点掌握整体链路的路由信息后再分析中断概率的这种做法并不可取。这不仅会导致消耗过多的网络资源,而且会产生决策滞后于变化的情况。因此,为应对节点运动的随机性,节点对中断概率的分析,需将从整条链路角度出发,转换到从单个节点角度出发。此外,由于海上信道近似服从莱斯分布,因此需要重新计算在莱斯信道衰落下,端到端的中断概率，这将有助于通信资源分配策略的改进与优化。

本文算法针对动态多跳中继网络,旨在研究一种能够在降低节点间中断概率、满足通信需求的条件下,实现节点能效最大化的频谱和功率分配策略。对此,本文首先对莱斯衰落信道进行分析,求出满足端到端中断概率的最低发射功率。之后计算出节点为满足通信需求所需的最多子载波数。引入异步分布式定价算法,对所有子载波进行评估后,选择出合适的子载波组合,作为下一步的优化分配的备选。在上述两项前提的基础上,利用满足KKT条件的拉格朗日乘子法,确定实际所需的子载波数量,及对应子载波上的发射功率。最后在能效、中断率等方面,对本文算法进行了仿真分析。

1 系统模型

本文对低复杂度海上动态多跳中继网络进行探讨，图1给出了系统模型的示意图。

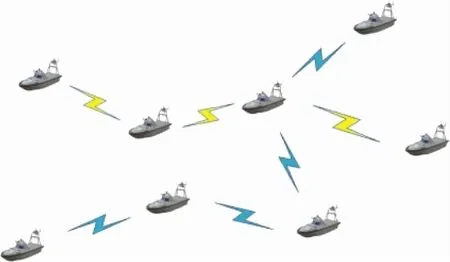
图1 系统模型Fig.1 System model

如图1所示,由于距离较远,源节点与目的节点之间没有直接相连的链路,因此源节点将通过多个中继节点与目的节点通信。网络节点采用频分多址的工作方式。在无线电系统所使用的频谱中,数个频段会被选用为公共控制信道,剩余个频段用作供节点传输信息的子载波。所有子载波均为莱斯衰落下的独立信道,背景噪声方差为。每个子载波具有相同的带宽,且子载波带宽远小于相关带宽。网络中所有节点都具有认知能力,不同节点可对同一子载波复用,记节点选用子载波的集合为。节点采用半双工DF协议,在不同时隙内进行信息的接收和发送。节点配备两根天线,一根用于在发送信息时检测冲突情况,另一根用于正常的接受和发送信号。节点每次转发信息时,会根据通信速率要求与信道质量的感知结果重新选择子载波组,并重新调整发射功率。当网络中的节点在发送信息时,检测到其他节点发来了信息,该节点将通过公共控制信道,告知向其发送信息的节点延时发送。

2 分析满足中断需求的功率

在海上通信时,接收端不仅会接受到一个主导的稳定信号,还会接收到信号的多径分量,故海上信道可近似服从莱斯分布。给出莱斯分布定义为

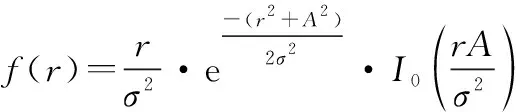
(1)

式中:表示正弦信号加窄带高斯随机信号的包络;表示主信号幅度的峰值;表示多径信号分量的功率;()为零阶第一类修正贝塞尔函数。

定义因子：

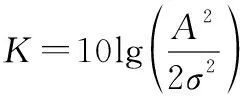
(2)

该因子是主信号功率与多径信号功率之比,反映了主信号起到主导作用的程度。

服从莱斯分布的信号其累计分布函数表示如下：

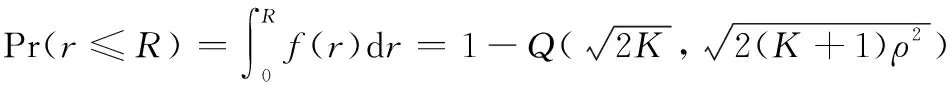
(3)

式中:表示归一化信号电平,定义为

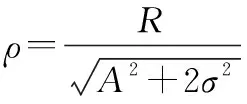
(4)

式中:(,)为Marcum函数,定义如下:

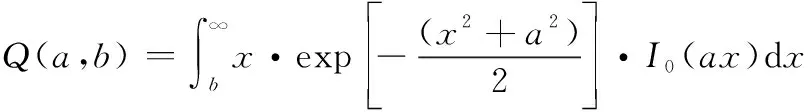
(5)

由于Marcum函数目前尚未找到闭式积分结果,因此采用数值积分方法进行计算。根据华军等人的研究成果,可以得到Marcum函数稳定计算的算式为

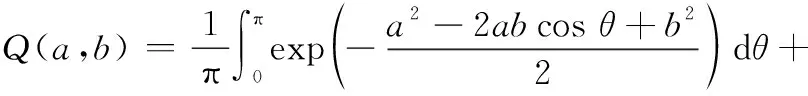
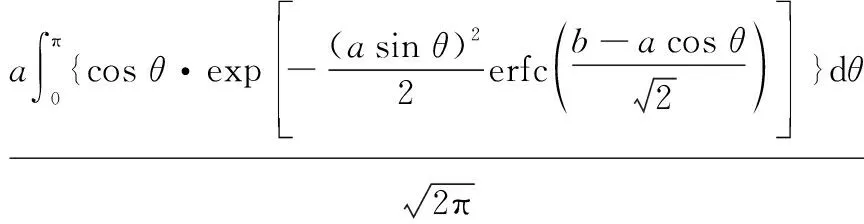
(6)

记表示链路上的路径损耗,表示为

=10lg()+

(7)

式中:为传播损耗指数;为节点间距离;为具有零均值的复高斯随机变量。式(7)的计算结果以分贝为单位。

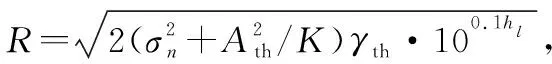
3 选取备选子载波组

节点在求得最小发射功率后,确定其所需最多子载波数,并从认知谱中选出对应数量的子载波,组成备选组。

节点在处于接受状态时,确认下一时隙待传输的信息总量,进而得到下一时隙需求的最小传输速率-。节点在下一时隙待传输信息列表中,找到最远目的节点,计算出与最远目的节点间的信道增益后,发射功率取为相应的,可获得的传输速率为

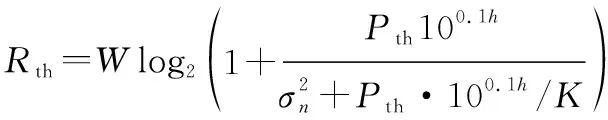
(8)

依据式(8),可求得节点需求最多的子载波数为

(9)

节点对认知频谱进行感知,并从中选择-max数量的子载波。对子载波的选择可抽象为背包问题。背包问题是一种组合优化的NP完全问题,用于描述如何选择最合适的物品放置于给定的背包中,使得背包内物品价值总和最高的问题。依据背包问题的理念,节点在选用子载波时,应使得子载波带来的收益总和最大化。

由于认知频谱中的子载波可多节点复用,对子载波的选取,以减少对其他节点产生的同频干扰为目标。为满足要求,本文引入异步分布式定价算法,对在不同子载波上可获得的收益做出评估：

(10)

式中:表示节点受到的干扰。式(10)反映了节点在子载波上获得的收益。在式(10)中,第1项表示节点在该子载波上可获得的通信速率，第2项为代价,表示节点每使用一单位的发射功率,对其他节点通讯速率产生的影响。其他复用同一子载波的节点提供干扰价格函数,构成节点代价函数。由于节点探测距离有限,若所有节点互相交换干扰价格信息,将耗费大量时间资源,并产生滞后性问题。因此,在计算代价时,节点仅与探测到的节点交换干扰价格信息与备选子载波组。依据式(10),节点通过博弈选取子载波,可实现降低或规避干扰的目的。

对于组内的子载波,节点并不一定要全部使用。未使用的子载波,在分配完成后会给予释放。

4 约束优化问题求解

在确定备选子载波组后,节点从其中选用个子载波,并相应地为之分配功率。

本文算法的目标是,在满足中断概率需求和通信速率需求的基础上,实现网络能效最大化。目标的约束优化问题表示为

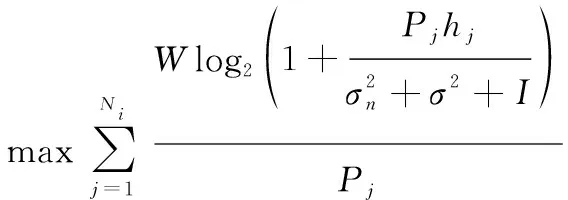
s.t.

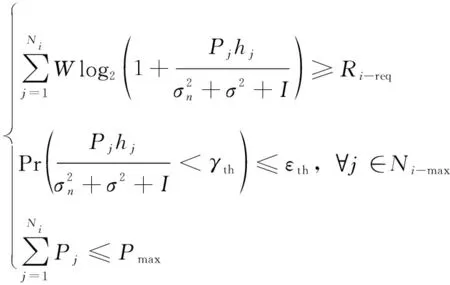
(11)

式中:第1项约束表示节点在所选用的所有子载波上,能够达到的通讯速率总和应大于等于任务需求;第2项约束表示在任意所选用的子载波上,节点通信应满足中断概率需求；第3项约束条件表示节点在所选用的所有子载波上,发射功率的总和应小于最大发射功率。

借由前文中的分析,式(11)中的第2项约束可等价于

≥-th, ∀∈

(12)

式(12)中各子载波上的-th并不完全相同。

针对式(11)所表示的约束优化问题,使用拉格朗日乘子法,可得到封闭形式的表达式。表达式为

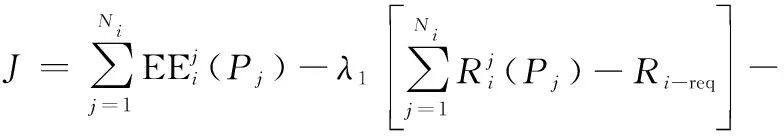
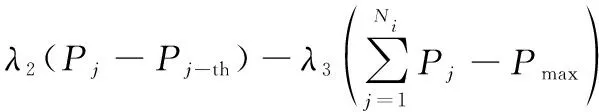
(13)

为求得最优解,对式(13)依次求关于各个,以及,,的偏导数,得

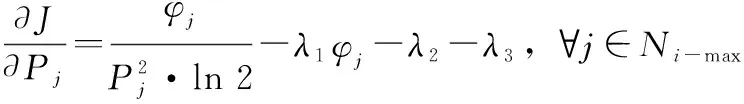
(14)

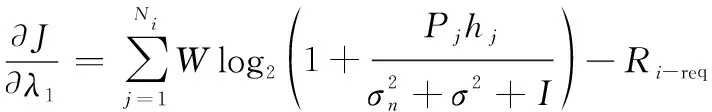
(15)

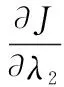
(16)

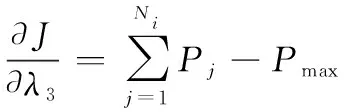
(17)

式(14)中,

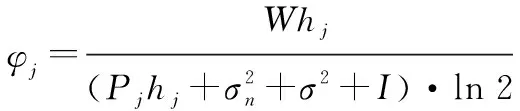
(18)

式(13)本应对所有功率值求偏导数,但由于这些偏导数表达式形式一样,仅针对的子载波不同,故由式(14)表示。

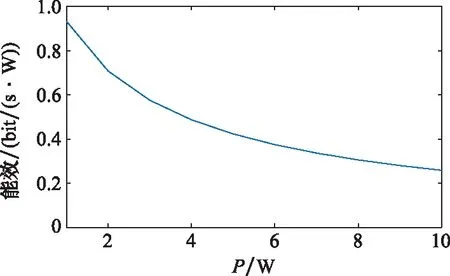
图2 能效函数Fig.2 Energy efficiency function

由图2可知,降低功率可带来能效的增加。对能效函数进行分析后发现,能效函数对功率的一阶导数小于零,二阶导数大于零,这使得节点降低一单位功率增加的能效量,要大于增加一单位功率减少的能效量。故节点均匀分配功率并不能最大化能效。此外,由于载波的莱斯衰落分布是独立的,若盲目采用均匀分配的策略,可能在部分子载波上无法满足中断概率的需求。因此,令式(17)等于零求解时,节点采用均分策略不一定是合适的。

在-max中任取两个子载波与,对于子载波和,令式(14)等于零,联立方程,可计算得

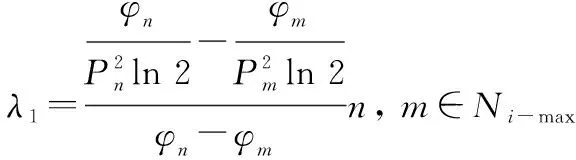
(19)

式(19)中的与,可在对第个和第个子载波分配功率求解时得出,分配功率求解过程如下。将式(19)代入式(14),记+=,为一常数。令式(14)等于零,经化简得

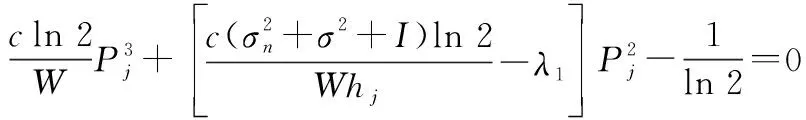
(20)

依据盛金公式法,计算得

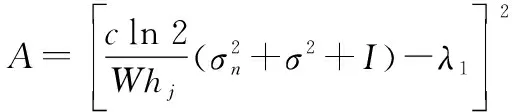
(21)

(22)

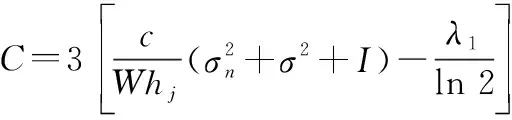
(23)

判别式如下：

Δ=-4>0

(24)

依据盛金公式法的原理,当Δ>0时,式(20)将存在一个实根和一对共轭虚根。该实根可表示为

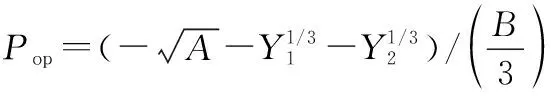
(25)

式中:

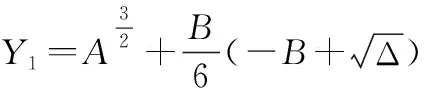
(26)

(27)

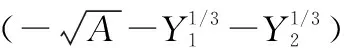
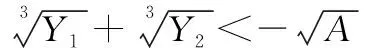
(28)

将式(26)与式(27)代入式(28),并引入不等式

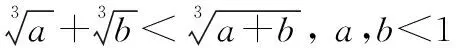
(29)

式(28)转化为

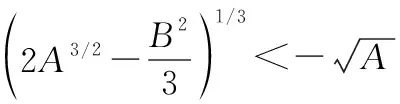
(30)

经过进一步计算可化简为

>932

(31)

将式(21)与式(22)代入式(31),可得

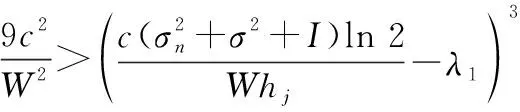
(32)

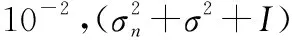
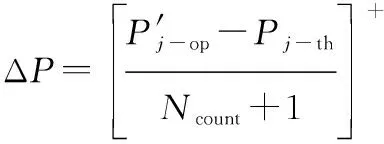
(33)

式中：[]=max{,0}；为迭代次数。令

=+Δ

(34)

依据式(34),对各个子载波上的发射功率取值。依次对不同子载波进行迭代运算,计算在其他子载波上功率为的情况下,各个子载波上可实现能效最大化的功率。在>10后,停止迭代运算。

按照上述的计算方式,在-max中的所有子载波上,节点计算出在各个子载波上的最优发射功率后,可能会出现节点的功率消耗总合大于的情况。若出现该情况,节点需从-max中进行挑选,从中选出个。被挑选子载波上的功耗总和应小于最大发射功率,并且要使得数量最大化。对于未被选用的子载波将予以释放,并通过控制信道,向最大探测范围内的其他节点传递告知信息。至此,完成频谱资源的分配,然后开始传输信息。

5 仿真分析

现考虑一个包含20个节点的多跳中继网络,节点于100 km×100 km范围内随机运动。节点最大时速为25节,节点速度及运动方向会发生变化。对于系统认知频谱,除去公共控制信道,设定剩余16个可供通信的子载波,每个子载波的带宽为25 kHz。所有子载波具有相同的背景噪声,功率为100 mW。节点的最大发射功率为30 W。节点最大探测距离为20 km。设定在接收端处,当信干噪比小于1时,节点间通信中断。节点间通信的中断概率上限阈值为1%。因子取值为10。节点间距离以km为单位,路径损耗指数取值为1.6。假设节点将全部功率用于发射信号,故系统损耗不予考虑。网络内信息的产生服从泊松分布。

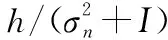
图3给出了两种算法系统吞吐量的对比图。图3中画出了两种算法能够达到的吞吐量以及基本需求。基本需求表示在每个时隙内,网络中所有节点需要传输的数据总量。由于信息的产生具有随机性,故在不同时隙网络能够达到的吞吐量起伏变化较大。从图3中可以看出,本文算法在吞吐量方面相较于对照算法有提升,但是提升程度不大。通过分析对照算法吞吐量小于本文算法的原因,发现是因为在对照算法中,若节点在某个时隙内需要传输消息过多,会导致在某些子载波上分配到的发射功率较小,进而会导致链路中断,损失掉在这些子载波上的数据传输量。在仿真过程中,部分节点确实会面临多路信息汇集的情况。因此,图3也从侧面印证了节点在面对有大量数据包需要传输时,本文算法相较于对照算法是有优势的。

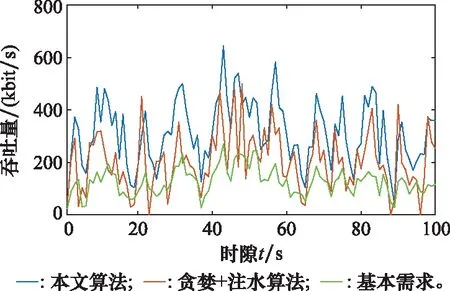
图3 系统吞吐量对比Fig.3 Comparison of systems’ throughput

图4给出了在每时隙内两种算法系统能耗对比图。图5给出了在每时隙内两种算法系统能效对比图。在仿真过程中,节点采用本文算法选用子载波的数量会小于等于对照算法下的需求量。正是因为子载波数量较多,采用注水算法不可避免地要使用更多的功率。故本文确实可以减少发射功率的消耗。因此,采用本文算法节点可减少能量消耗,提高能效。

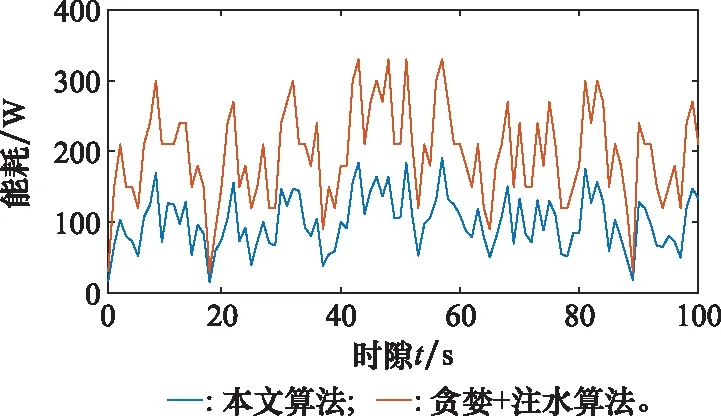
图4 系统能耗对比Fig.4 Comparison of systems’ energy consumption

图5 系统能效对比图Fig.5 Comparison of systems’ energy efficiency

图6给出了在所有时隙内,两种算法中节点平均能耗对比图。图7给出了在所有时隙内,两种算法中节点平均能效对比图。由于节点运动具有随机性,故不同节点在区域内的位置会有较大差异,从而导致不同节点作为中继的次数不尽相同。图6与图7也印证了本文算法在提高能效方面具有优势。

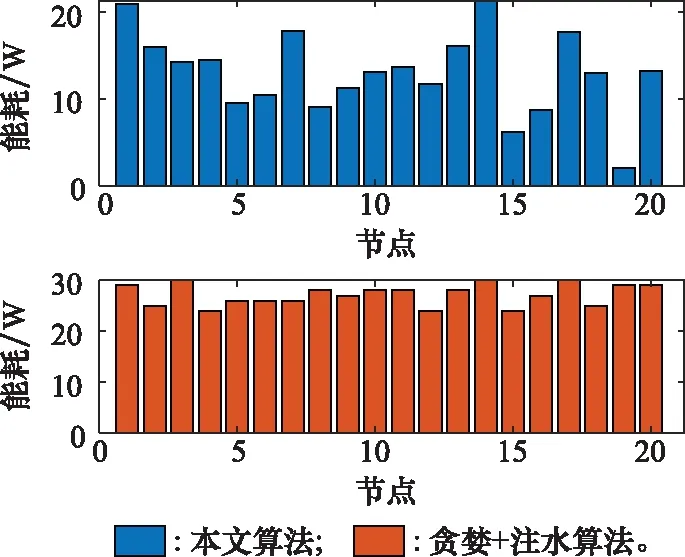
图6 节点平均能耗对比Fig.6 Comparison of nodes’ average energy consumption

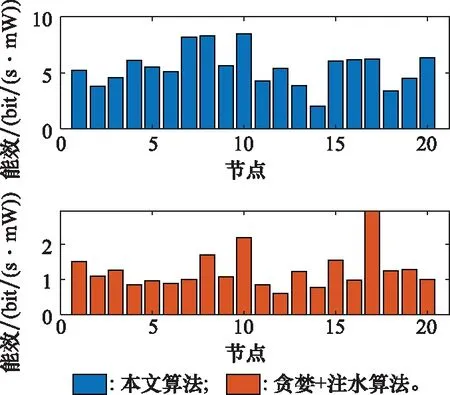
图7 节点平均能效对比Fig.7 Comparison of nodes’ average energy efficiency

图8给出了在每个时隙内,两种算法网络发生中断的次数对比。图9给出了在两种算法中,所有节点在全时隙内的平均中断概率。仿真结果显示,节点间的平均中断概率达到了4%,超过了前文中计算时设定的中断概率阈值1%。通过分析发现,节点在选取子载波时,由于不会与超出界限的节点交换发射功率和干扰价格信息,此时,若某一在发射节点界限以外,接受节点界限以内的节点,使用了与发射节点相同的子载波,则会在接收端处产生较大的干扰,有可能会导致中断。而对照算法产生较大中断率的原因在前文已分析过,不再赘述。

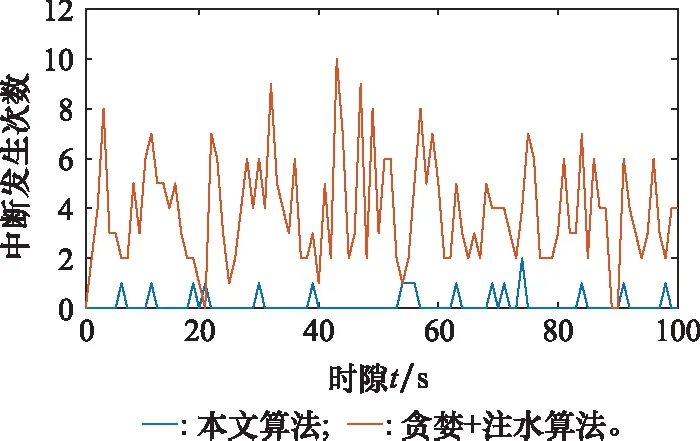
图8 系统中断次数对比Fig.8 Comparison of the number of outage

图9 节点平均中断率对比Fig.9 Comparison of nodes’ average outage rate

对任意节点而言,记其探测范围内其他节点数量为,本文算法与对照算法的乘法运算复杂度如表1所示。可见,本文算法是以牺牲算法复杂度为代价获得了效能上的提升。

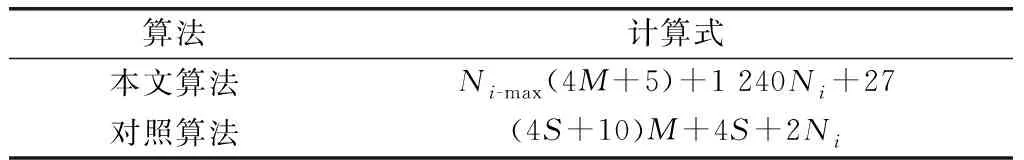
表1 算法复杂度

通过仿真分析可以看出,即使是在节点平均中断率较高的前提下,对照算法在吞吐量性能上的表现依然不是很差,可见对照算法在提升系统整体吞吐量方面依然是有可取之处的。但是其在保证网络链路的稳定性方面有所欠缺,且能量效率比较低。由此可见,在面对不稳定的海上通信时,为保证较高的能量效率,本文算法是有效的。

6 结 论

本文针对海上无人艇构成的多跳中继网络的场景,围绕如何分配通信资源可使能效最大化展开研究。基于对莱斯衰落信道的分析,对满足中断概率需求的最低发射功率进行求解。进而确定节点所需最多子载波数量,并引入异步分布式定价算法,从频谱中选取备选组。最后,利用满足KKT条件的拉格朗日乘子法对频谱和功率资源分配的次优解进行了求解。仿真结果表明,本文算法在保证通信需求的同时,可以大大降低中断发生的概率,且能够有效提升系统整体的能效。