基于a&ω六自由度运动模型的船舶运动参数发生器

2022-08-17卞鸿巍祝中磊王荣颖

系统工程与电子技术 2022年8期

卞鸿巍, 祝中磊, 王荣颖, 马恒, 文者

(海军工程大学电气工程学院, 湖北武汉 430033)

0 引言

航海模拟器是一种用于船舶模拟训练的仿真平台,通过虚拟现实技术、船舶运动仿真与控制技术模拟船舶在海洋中的运动,可以为操作者提供真实环境的感受和操作体验,提升其操纵驾驶能力。船舶运动数学模型是船舶运动仿真与控制的核心,根据船舶自身与海况环境信息生成航海模拟器所需的船舶运动参数。

目前,最具代表性的船舶运动数学模型主要有分离型模型、整体性模型和响应性模型3类。整体性模型和响应性模型结构简单,多使用系统辨识方法进行参数确定;分离型模型则由于具有建模方式灵活、水动力参数意义明确等优点,被应用在一系列复杂船型中。国内外多位学者针对不同类型的船舶,大都基于上述3类模型和改进,开展相应研究。如文献[14]对气垫船的操纵运动进行建模仿真,较详细地分析了回转运动过程中气垫船的侧漂、内倾以及风力对气垫船的影响;文献[15]利用非线性时域条带法对高速滑行艇结构响应以及流体力学和结构惯性载荷和运动响应展开了研究;文献[16]为模拟拖轮协助大型船舶的操纵过程,采用分离型模型的建模思想,建立了相应的船舶运动数学模型等。

对于运动状态模拟仿真精度和操控逼真性要求突出的应用场合,上述方法存在船舶运动数学模型的有效性难以验证的问题。主要原因如下:一是由于实船的六自由度船舶数学模型较为复杂,大多学者根据现实需求建立简化模型,仿真出的船舶运动参数较为理想化,与船舶实际运动效果存在较大差异;二是因实验成本高、周期长,导致建立船舶运动数学模型所需的实验数据较难获取;三是缺乏统一、完备的验证评估体系,如大多学者仅针对船舶模型的旋回性进行验证,未评估模型在船舶加减速等机动情况下的性能。

针对上述问题,本文提出了一种新的船舶运动参数发生器设计方法。该发生器的设计思路为:① 在船舶运动响应模型的基础上,分析船舶在各种机动状况下的线加速度与角速度(linear acceleration and angular velocity,&近似解析表达式,建立基于&的船舶运动模型;② 采取递推最小二乘法估计模型中的未知机动参数,并基于建模得到的线加速度与角速度,通过船舶运动微分方程生成六自由度的船舶运动参数信息;③ 为各船舶运动参数设定相应的模拟仿真精度阈值,根据阈值建立相似度评估指标,以验证采用发生器进行仿真分析的有效性。

与传统船舶运动数学模型相比,该发生器的模型需估计的未知参数少,因此对实验数据的要求低,有效降低了建模难度。通过采集的实船实测数据,对建立的模型在船舶的各种复杂机动下进行了仿真验证和相似度评估。结果验证了方法的有效性。

1 基于a&ω六自由度运动模型

本文采取的船舶运动模型定义为在船舶自身机动作用下船舶加速度和角速度的方程。为展示建立&六自由度运动模型的完整步骤,绘制利用实测数据搭建模型的流程如图1所示。

图1 利用实测数据搭建船舶运动模型的流程Fig.1 Process of building ship motion model using measured data

为方便叙述,本文首先介绍了船舶运动模型的建立,然后在船舶运动参数的求解小节中讲述了采用递推最小二乘法估计模型中的未知机动参数的方法。图1中的实测数据预处理与机动情况分析的主要作用是对采集的实测数据进行降噪处理,并分析采用递推最小二乘法进行参数估计时所需的测量输入值(计划航速变化量Δ和舵角),该部分内容本文暂不赘述。

下面以船舶计划航速变化量Δ、舵角为输入量,针对船舶各种机动情况,分别讨论分析船舶线加速度和航姿角速度的表达式。

1.1 船舶航姿角速度

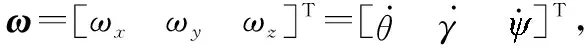
111 纵摇角速度

由于船舶复原力矩较大,船舶在静水中运动时纵摇角通常保持在零附近,可认为船舶纵摇角速度也近似为零,即=0。

112 横摇角速度

船舶在静水中匀速、变速直线运动时的横摇角近似为零,而在回转运动时,由于离心加速度的影响,船舶会横倾一定角度。这一过程中横摇角()可采用下述函数模拟:

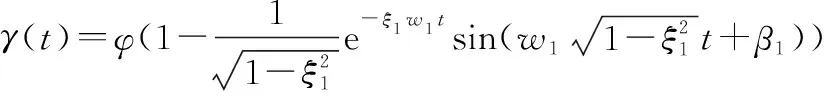
(1)

式中:、、分别表示横摇角变化的阻尼比、振荡频率、初始相位,为自定义参数;为船舶回转运动定常阶段时的横倾角,由文献[28]可知

(2)

式中:表示船舶的纵向加速度；表示重力加速度。

在回转运动结束时,船舶由横倾逐渐恢复为平稳状态,此时横摇角()可表示为

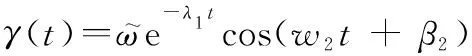
(3)

式中:、、分别表示衰减系数、振荡频率和初始相位,为自定义参数。对式(1)和式(3)求导即可得到横摇角速度。

113 航向角速度

由经典的Nomoto响应模型可知,航向角速度与舵角的关系为

(4)

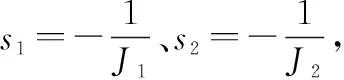
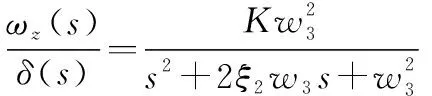
(5)

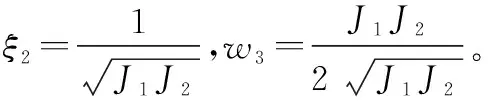
设舵角为幅值为的阶跃响应时,航向角速度时域表达式为

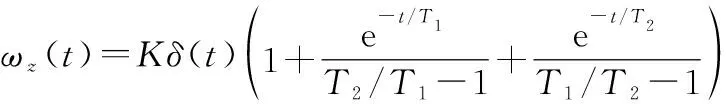
(6)

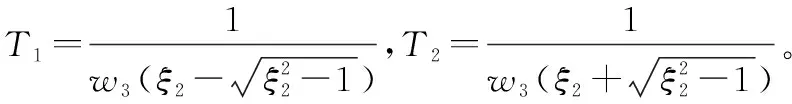
1.2 船舶线加速度

为方便描述、简化分析,定义一个新坐标系系:其坐标系原点为船舶质心,轴在水平面内沿船舶横向指向右方,轴沿船舶纵轴指向船艏,轴方向由右手法则确定。

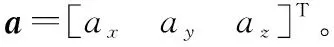
121 横向线加速度

船舶在直线运动时,横向线加速度近似为零;船舶在回转运动时,横向线加速度充当船舶的离心加速度。设此时航向角速度为、纵向速度为,由文献[28]可知

(7)

122 纵向线加速度

船舶在匀速状态下纵向线加速度=0,在变速状态下≠ 0。下面以船舶变加速为例求解的近似解析表达式。

分析大量实测数据可知,船舶加速时的速度曲线与二阶系统阶跃响应曲线较为相似。因此,本文采用二阶系统阶跃响应函数作为船舶加速时纵向速度的近似解析表达式,对其求导后得到船舶线加速度。

设某一时刻(为简化分析设为零时刻)船舶纵向速度为,计划航速增加Δ后,纵向速度近似解析表达式为

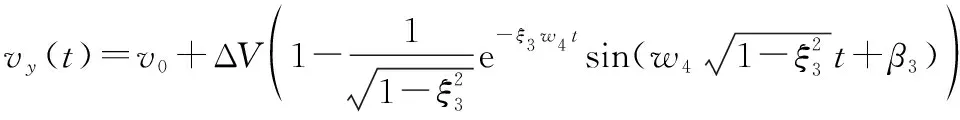
(8)

123 天向线加速度

船舶在静水环境中运动时,在天向上的位移较小,因此船舶的天向线加速度可近似视为零。

由上述内容可知,以计划航速变化量Δ、舵角为输入,可计算出船舶机动线加速度与角速度,各分量求解流程如图2所示(与为零)。

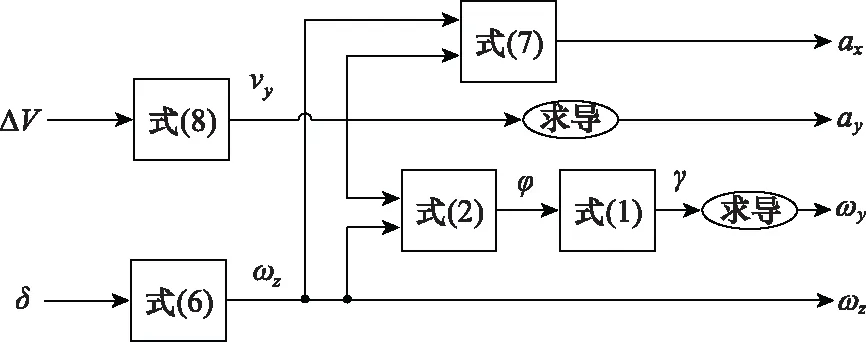
图2 a与ω的分量求解流程Fig.2 Solving process of a and ω component

2 船舶运动参数的求解

2.1 基于递推最小二乘法的参数估计

第1节讲述了船舶关键运动参数——加速度和角速度的模型,针对模型中的未知参数(见表1),可采用递推最小二乘法进行参数估计得到其估计值。

表1 未知参数列表

递推最小二乘法是一种基于无偏估计的辨识方法,其原理简单、易于实现。最小二乘法采用的模型结构为

()=()()+()

(9)

式中：()、()是系统连续输入和输出变量;()是零均值的白噪声向量。

将式(9)写成最小二乘格式,即

()=()+()

(10)

式中:()=[-(-1),-(-2),…,(-),(-1),(-2),…,(-)],为()分母中的未知参数的个数,为()分子中的未知参数的个数;为待估计的参数向量。

基于递推最小二乘法的参数估计算法1如下所示。

算法1 基于递推最小二乘法的参数估计输入:测量输入值u(k)、测量输出值z(k)输出:估计参数θ^步骤 1 设定初值:θ^=θ0步骤 2 估计参数θ^更新:θ^(k)=θ^(k-1)+K(k)[z(k)-hT(k)θ^(k-1)]步骤 3 增益矩阵K更新:K(k)=P(k-1)hT(k)[1+hT(k)P(k-1)hT(k)]步骤 4 矩阵P更新:P(k)=[I-K(k)hT(k)]P(k-1)

2.2 船舶运动微分方程

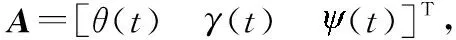
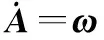
(11)

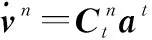
(12)

(13)

式(12)和式(13)中:

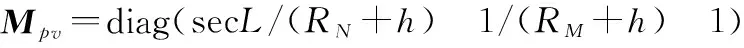
(14)

(15)

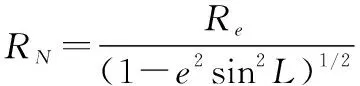
(16)

(17)

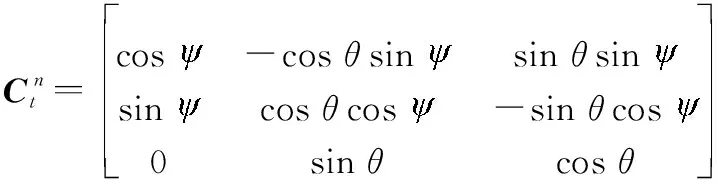
(18)

式(15)和式(16)中,、为地球长半轴半径和扁率,可分别取=6 378 137 m,=1298 257。

3 评估指标

为评判本文的仿真结果与实测数据的相似程度、验证建模方法的有效性,需建立评估船舶各运动参数的基准真值与评估指标。以组合接收机的位置信息、多普勒测速仪的速度信息、惯导的姿态信息作为基准,为减小测量噪声的干扰,采用小波变换对各导航信息滤波。为评判发生器的仿真效果,提出相似度评估指标,下面介绍计算步骤。

(1) 计算每一时刻(记为时刻)仿真数据与实测数据之间的误差:

(19)

除位置误差外,其余运动参数(如航速、纵摇、横摇等)均根据式(19)计算,位置误差的计算方法为

(20)

式中:、为仿真数据的纬度与经度;、分别为实测数据的纬度与经度。

(2) 将误差与阈值Thr进行比较,如果在阈值范围内则视为正确,如果在阈值范围外则视为错误,

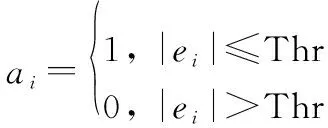
(21)

(3) 计算所有时刻仿真数据的准确率,定义相似度为

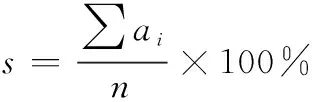
(22)

式中:为数据长度。

4 试验验证

为验证本文方法的有效性,分析船舶在自身机动作用下的船舶运动模拟仿真情况,选取一段海面较为平静且在建模时未用过的实测数据进行仿真(船舶参数如表2所示)。该段数据对应的船舶机动状况如表3所示。表中模拟舵角值由船舶回转运动稳定时的航向角速度,除以式(6)中的值得到;表中“直线”主要是相对于回转运动而言,此时模拟舵角值为零,由于船舶实际回转运动过程的舵角未知,而模拟舵角值与舵角成比例变化,因此以模拟舵角值替代舵角值。由表3可知,该段实测数据中,包含直线匀速、直线加速、回转加速、回转减速等船舶多种机动状况,能够更全面测试本文模型对船舶运动的模拟效果。

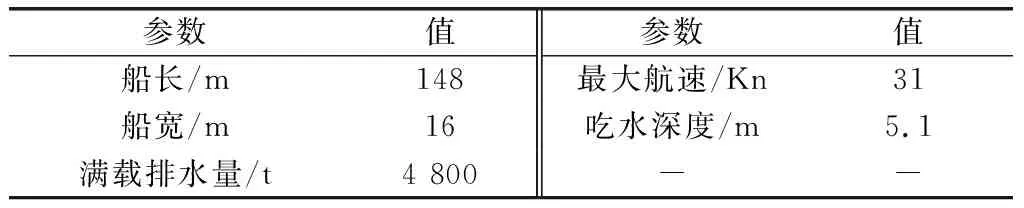
表2 船舶参数

表3 机动状况

船舶初始位置为经度122.904 8°、纬度30.858 1°,初始速度为5.28 m/s,初始航向角为135°,横摇角为1°,纵摇角为0.1°。由表3中的船舶机动状况信息,通过船舶运动参数发生器仿真船舶各主要运动参数,如图3所示。

图3中各运动参数下标为real表明该参数是实测数据,下标为simulation表明该参数是仿真数据。由图3(a)可知,在第一个回转运动以及随后的直线运动时,仿真航迹与实测航迹较为接近,表明模型能很好地根据船舶实际的机动情况仿真出船舶实际的航迹;在第二个回转运动过程中出现一定的偏差,这可能与第二次回转运动过程中多次打舵有关,因为表3中的机动状况是由实测数据分析得到,并非船舶实际运动过程中的机动情况,存在一定误差。由图3(b)可知,除110～260 s仿真速度与实际航速误差相对较大外,其余时间段仿真效果较好,分析可知在110 s时刻船舶开始加速时仿真可能有所滞后。由图3(c)和图3(d)可知,仿真纵摇角和横摇角能很好地模拟出实测数据的趋势。由图3(e)可知,仿真航向与实测航向较为接近,结合图3(b)的航速图,从侧面说明了图3(a)中航迹仿真偏差较小的合理性。

为更直观评判仿真结果与实测数据的相似程度,计算各主要运动参数的相似度指标和均方根误差(root mean square error, RMSE)指标如表4所示。

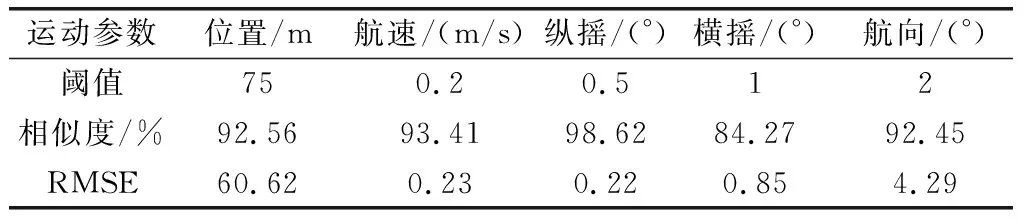
表4 各主要运动参数相似度与RMSE

相似度指标反应了可接受的误差范围(阈值)内的准确率,RMSE指标反应了误差统计规律。从理论上说,RMSE值越小,相似度评估指标越高;同时,相似度的值与阈值有关,其值可根据各船舶运动参数的模拟仿真精度要求设定。与RMSE评估指标相比,本文中提出的相似度评估指标采用百分比的形式展示,更为直观。由表4可知,在针对不同运动参数设置相应的阈值后,各主要运动参数的相似度均达到80%以上,且RMSE维持在阈值附近。这也从指标上说明了采用本文船舶运动参数发生器能较好地模拟船舶在多种机动状况下的运动,比较贴近实际,本文方法的有效性得到验证。

传统整体型、分离型数学模型建模时所需的流体动力导数、水动力系数等参数的测定成本高、实验花费大,且其仿真试验需对船舶的桨力与舵力等进行赋值,然而在实船运动时这些数据难以获得。因此，基于现有导航装备采集的船舶位置、速度、姿态等数据,无法利用整体型、分离型数学模型进行仿真对比分析。为体现本文方法的优越性,本文采用文献[30]中的方法进行对比仿真。文献[30]中,将船舶的运动状态假设为匀速、匀加速(匀减速)以及匀速圆周等理想化运动状态。船舶参数和船舶机动情况仍如表2和表3所示,位置误差的仿真结果如图4所示。

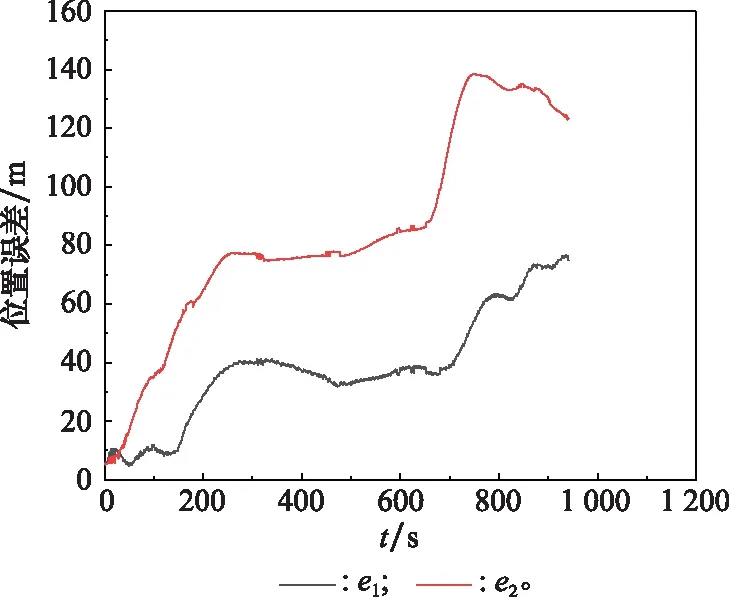
图4 位置误差对比图Fig.4 Comparison diagram of position error

图4中,、分别为采用本文方法和文献[30]方法仿真得到的位置误差曲线。由图4可知,在船舶运动900多秒后,文献[30]仿真得到的位置误差已超过120 m,且经计算位置相似度仅为25.59%,这主要是由于文献[30]采用匀速、匀加速等理想化运动状态导致存在较大的累积误差;而本文方法的位置误差为70 m,位置相似度为92.56%,仿真精度得到极大提高。