混合分数布朗运动下欧式期权模糊定价研究
2022-08-16林先伟秦学志
林先伟, 秦学志, 尚 勤
(大连理工大学 经济管理学院,辽宁 大连 116024)
0 引言
金融市场经常受到一些模糊不确定因素的影响,使得金融衍生产品的定价具有模糊特征。Zadeh提出的模糊集理论很好地解决了这类问题[1]。近年来,模糊集理论作为一种有用的工具在金融衍生产品定价中得到了广泛的应用。Wu[2]基于Black-Scholes模型得到了欧式期权的模糊价格,并给出了任意给定期权价格的置信度。Zhang等[3]提出了标的股票价格、无风险利率和波动率为模糊数时的几何亚式期权模糊价格。Qin等[4]用模糊数刻画到期时标的股票价格的不确定性, 在此基础上研究了长记忆性特征下的两值期权模糊定价问题。马勇等[5]研究了基于模糊环境下欧式障碍期权定价问题, 得到了欧式障碍期权的显示解。Li等[6]提出了一种带模糊参数的欧式期权定价方法,得到了模糊期权价格。Lu等[7]给出了不确定股票市场下欧式期权的定价公式。
根据分形市场理论,长记忆性描述的是序列的高阶相关结构。在股票市场中,长记忆性是指不同时期的股票价格在相隔较远时仍然具有一定的相关性,过去的价格信息会对未来的价格产生长期持续的影响[8]。相关学者通过一系列的实证研究发现金融市场存在显著的长记忆性[9,10]。Peters[11]基于分形理论将Hurst指数引入金融领域,作为衡量长记忆强度的指标。李大夜[12]建议可以用确定时间标度下的局部Hurst指数研究市场趋势。为了刻画金融市场的长记忆性特征,相关学者采用了分数布朗运动模型来描述资产价格的变化。然而, 分数布朗运动不是半鞅,很难定义关于分数布朗运动的随机积分。为了解决这一问题,Shiryae等[13]提出用混合分数布朗运动模型来刻画金融资产的价格变化过程,并进行相应的期权定价。混合分数布朗运动本质上是布朗运动和分数布朗运动的线性组合的高斯过程族。Cheridito[14]证明了在Hurst指数条件下,混合分数布朗运动等价于标准布朗运动,因此金融市场不存在套利机会。Xiao等人[15]讨论了混合分数布朗运动环境下的股权权证定价模型,给出了解析解。Sun[16]研究了混合分数布朗运动环境下的外汇期权定价模型。Rao[17]利用混合分数布朗运动刻画股票价格的变化过程,得到了混合分数布朗运动环境下亚式期权的定价公式。Ahmadian[18]假设股票价格服从混合分数布朗运动,得到了混合分数布朗运动环境下亚式彩虹期权的定价公式。
综上所述,本文提出了一种新的欧式期权糊定价模型,该模型考虑了股票价格的长记忆性特征。在这里,本文假设,相关的实证研究已经验证了这一假设是有效的[19]。本文的学术贡献主要体现在:首先,为了刻画金融市场的长记忆性特征,采用混合分数布朗运动去描述股票价格的动态变化;其次,在混合分数 Black-Scholes 模型的基础上, 基于标的股票价格、无风险利率和波动率均是模糊数的假定下,构建了欧式期权模糊定价模型,进一步的补充了现有文献的不足; 最后,分析了金融市场长记忆性的度量指标Hurst指数H对定价模型的影响,并通过数值实验检验了该定价模型的可行性和合理性。

1 基础知识
1.1 混合分数布朗运动[16]

(1)
其中α和β都是不为0的常数。
混合分数布朗运动有如下性质:

(2)
(3)
(vi)对所有t∈R+
(4)






(5)

(6)

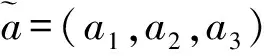
(7)
(8)


(9)

(10)
2 混合分数布朗运动下欧式期权模糊定价模型
2.1 混合分数布朗运动下欧式期权定价模型
设(Ω,p)是一个具有σ-流的完备的概率空间。Ft是由BH(t)生成的σ-流,p表示真实概率测度。现在考虑混合分数Black-Scholes市场有两种资产,设债券价格Mt满足下面方程:
dMt=rMtdt,M0=1,0≤t≤T
(11)
其中r表示无风险利率。
股票价格St满足下列随机微分方程:
(12)
其中μ,σ分别表示预期收益率和波动率。

(13)
那么可以得到
(14)
参考文献[16],以股票价格St作为标的、K为敲定价格、带有到期日T的欧式看涨期权在时刻t的价格为
Ct=f(St,T,t,H,K,r,σ)
=StN(d1)-Ke-r(T-t)N(d2)
(15)
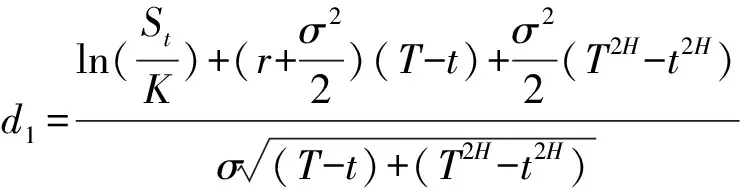

2.2 混合分数布朗运动下一般模糊定价模型
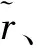
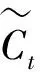
(16)

金融市场的长记忆性可以用Hurst指数H来度量,下面的定理表示了Hurst指数对欧式期权模糊价格的影响。
定理2Hurst指数对欧式期权模糊价格的影响
(17)

(18)

(19)
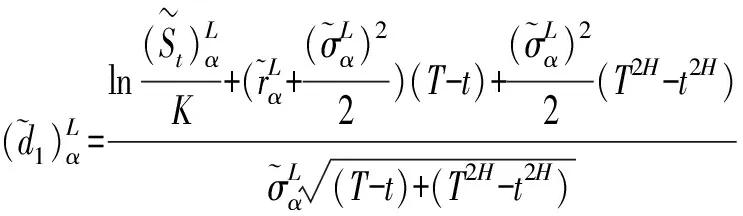


(20)
(21)

(22)

(23)

2.3 混合分数布朗运动下具体模糊定价模型
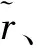


(24)
(25)
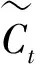


2.4 任意给定期权价格的置信度

(26)
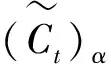
对于等式(26),对于任意给的那个的欧式期权价格c,它的置信度α可以通过以下的优化问题可以得到,具体可以参照Wu[2]。
3 数值实验


表1 基准模型参数的取值
3.1 任意给定的欧式看涨期权价格c的置信度

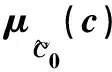
表2 对任意给定的欧式看涨期权价格c对应的置信度

图1 Hurst数对期权价格的影响

图2 Hurst指数,到期日对期权价格的影响
3.2 长记忆性的度量指标Hurst指数对该定价模型的影响

表3 不同下欧式看涨期权模糊价格的α-截集区间

3.3 稳健性分析
为进一步分析模型参数的敏感性,下面通过控制变量法分析模型的稳健性。
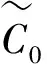

表4 随机模型欧式期权价格和模糊随机模型欧式期权模糊价格的α-截集

这表示欧式期权价格的平均水平是3.4028,风险是0.1699。
4 结论
欧式期权是金融市场上流行的金融衍生产品,对其准确定价具有重要的理论和实践意义。本文研究了基于混合分数布朗运动下欧式期权模糊定价问题,取得的主要结论如下:(1)采用混合分数布朗运动来刻画标的股票价格的动态变化,在股票价格、无风险利率、波动率均为模糊数的假定下, 构建了欧式期权模糊定价模型。(2)分析了长记忆性特征的度量指标Hurst指数H对定价模型的影响:当到期日0
