整体思想在初中数学解题中的应用——以“图形与几何”问题为例

林 芹 陈豫眉 （西华师范大学，四川 南充 637000）

著名数学教育家波利亚认为：“掌握数学就意味着要善于解题”.然而，善于解题并不意味着一味地使用自身熟悉的、做过的题型去“套”.这种只满足于解出答案，不对问题所蕴含的思想、方法进行归纳的学习方式已经无法满足学生内在发展的需要.因此，教师在教学中应该有意识地培养学生运用数学思想方法去分析问题和解决问题的能力，提高数学素养.

整体思想作为数学思想中的重要思想，旨在从已有问题的整体性质出发，认真观察问题的整体结构，对其进行恰当的分析与改造，把握住问题的整体结构特征，运用“集成”的眼光，将其中的某部分看成一个整体，挖掘式子或图形之间的内在联系，再对它们进行有目的、有意识的整体处理，使得原有式子或图形的结构变得更加清晰明了，容易解决.图形与几何问题较为重视推理过程，整体思想非常符合这一要求，它能将学生的思维过程有效地融合在一起，而又不至于太过分散.这种以整体的眼光看待问题、解决问题的方法，在解决图形与几何问题中发挥着不可替代的作用.

1 整体思想在求解图形面积中的应用

通过观察归纳，不难发现中小学阶段在求解图形面积的相关问题是有共通之处的.求解平面不规则图形的面积问题的解题关键其实就在于需将原有的不规则图形转化为规则图形求解，既能考查学生的读图、识图能力，又能考查学生的数学转化思想与思维的灵活性.而数学的整体思想恰好在这一类求解图形面积问题中发挥着不可替代的作用，在求解此类问题时，常常需要学生运用整体的眼光去看待原有的不规则图形，即从原有图形的局部结构特征入手，与其所学的规则图形关联起来，达到解决问题的目的.

如图1⊙⊙⊙两两不相交且半径都是0.5 cm求图中阴影部分的面积结果保留π

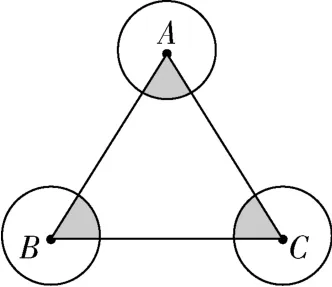
图1

本题若依据常规思路，我们会考虑分别计算各阴影部分的面积，再求和.但是，经过观察我们发现，尽管上述图形的阴影部分是规则图形扇形，但我们不知道每个扇形所对圆心角的度数，故无法顺利求解出每个扇形的面积.然而，若用整体的眼光去看待问题，由于三个扇形的半径均为0.5 cm，那么自然可以将三个阴影部分转换成一个半径为0.5 cm 的半圆，既打通了思维上的阻碍，还简化了计算的过程.

如图2在Rt△中∠＝90°＝4＝2分别以为直径画半圆求图中阴影部分的面积结果保留π

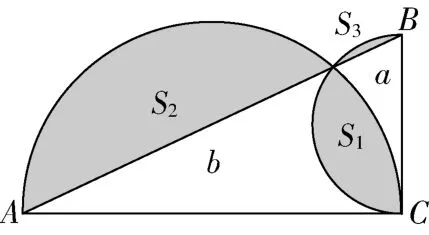
图2

本题若依据常规思路，我们首先考虑分别计算各阴影部分的面积，再求和.但是，经过观察我们可以发现，上述图形的阴影部分均为不规则图形，无法根据标准图形面积的计算公式直接计算.那么，我们可以转换思路，尝试利用差值思想，结合其他标准图形解决问题.然而，经观察思考发现其他图形中仍包含未知的不规则图形，也无法顺利解决问题.因此，先不考虑结论，我们先从已知的可利用的条件入手.将各部分阴影面积分别用，，，，来表示，再利用已知条件，建立三个等式：

如图3矩形被两条对角线分成了四个小三角形已知四个小三角形的周长和为86 cm一条对角线长为13 cm求矩形的面积.

图3

本题若依据常规思路，为求解矩形的面积，则需知道矩形的长和宽.但经过观察思考可以发现，由于已知条件不足，根本无法求解矩形相应的边长.然而，若运用整体思想，根据矩形面积公式＝·，只需求解出·的值.由题可知+++＝86-2（+）＝86-4×13＝34，可以得到+＝17.再将上述式子两边同时平方，可得+2·+＝289.又因为+＝13＝169，所以·＝60.

如图4两个正方形有一个公共顶点已知大小正方形的边长分别为求△的面积用的代数式表示

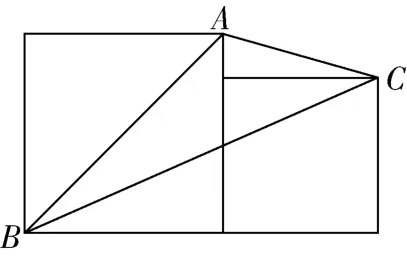
图4

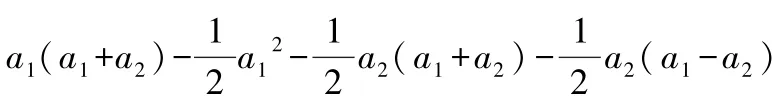
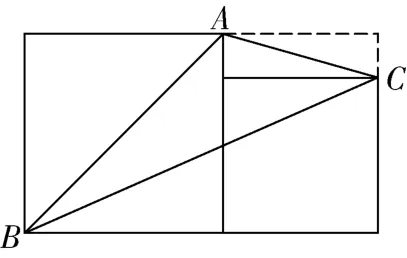
图5

通过观察上述问题，我们不难发现利用整体思想在求解图形面积问题中的关键是善于用“集成”的眼光.在求解此类问题的过程中，若拘泥于常规思路或解法，常常会发现无法运用现有的知识进行求解，即容易走入“死胡同”.但是，如若我们认真思考，从整体上去发掘解决问题的关键，把握图形的整体结构特征，便能使原有的问题化繁为简、化难为易，达到柳暗花明、豁然开朗的效果.

2 整体思想在几何问题中的应用

几何问题，说到底也就是图形问题，旨在研究图形的性质.这就要求学生能够分辨出题目所给出的信息，且能够洞察隐藏在已知图形下的与解决问题相关的另一“子图形”，再利用“局部”或“全局”的整体性，将二者恰当地结合起来，使得原来无从下手的问题，变得简单，解决问题的思路也变得清晰明了.

如 图6求∠1+∠2+∠3+∠4+∠5+∠6＝________.

图6

由图可知，∠1+∠2 ＝180°-∠，而∠＝∠，故∠1+∠2＝180°-∠①.同理∠3+∠4 ＝180°-∠②，∠5+∠6 ＝180°-∠③.由①+②+③可得∠1+∠2+∠3+∠4+∠5+∠6 ＝3×180°-∠-∠-∠而现在若想单独求解∠、∠、∠的度数，将会无计可施.但是，根据题意可知，需要求解的是∠1+∠2+∠3+∠4+∠5+∠6 的值.因此，我们不必拘泥于单个角的度数，应当从整体的角度入手，把握角与角之间的内在联系.∠、∠、∠是△的三个内角，根据三角形的内角和定理，可知∠+∠+∠＝180°.因此，我们只需将上述式子看成一个整体，就可得到∠1+∠2+∠3+∠4+∠5+∠6＝3×180°-（∠+∠+∠）＝3×180°-180°＝360°.

如图7已知在△中∠＝50°分别是∠和∠的平分线求∠的度数.

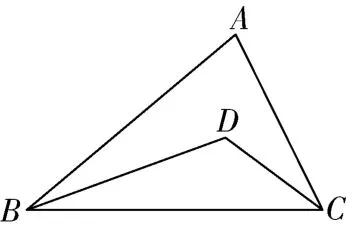
图7

如图8在平行四边形中∠＝70°∠＝∠并且平分∠求∠的度数.

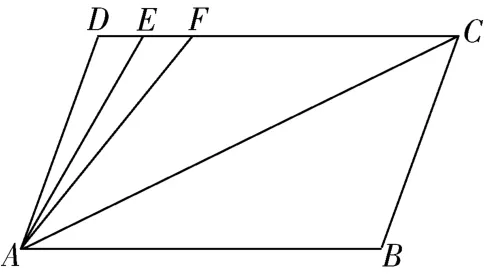
图8

根据图8 可知，∠＝∠+∠但想要求解∠的度数，无须分别求解两个角的度数，只需要运用整体思想，将∠和∠看成一个整体.根据题意可以发现，∠＝∠，又因为平分∠，∠＝70°.故可以得到∠＝∠+∠+∠+∠＝2（∠+∠）＝70°，即∠＝∠+∠＝35°.

图9

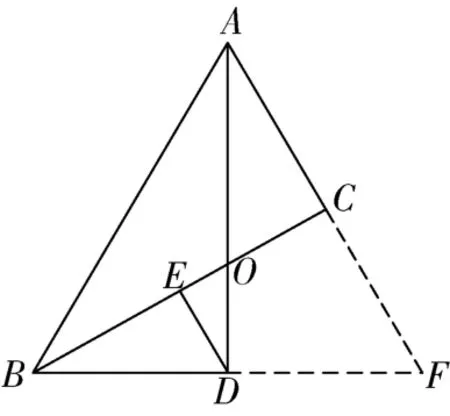
图10

综上所述，在求解某些图形与几何问题时，不要执拗于计算出某部分具体的值.应当从已有问题的整体出发，认真观察图形与几何的整体结构，运用“集成”的眼光，尝试将部分图形与几何看成一个整体，建立起局部与整体的联系，对它们进行有目的、有意识的整体处理，使原有图形与几何的结构变得清晰明了，使问题变得易于解决.