换元法在复合函数求导中的应用
2022-08-16覃桂茳罗秀峰黄丽清赵春茹覃学文梧州学院广西梧州54300长洲中学广西梧州54300
覃桂茳 罗秀峰 黄丽清 赵春茹* 覃学文 (.梧州学院,广西 梧州 54300;.长洲中学,广西 梧州 54300 )
引 言
在新课标理念的倡导下,对数学学科教学工作开展了一系列详细的规定,围绕数学课程设计、课程性质、课程内容与课程目标均有了确切的要求,可以说新的课程标准为教师提供了更清晰的教学思路与更精确的培养方向.高二数学(人教版)选学2-2 第一章“导数及其应用”的教学理念是“实践——理论——实践”,先通过瞬时速度、切线斜率的极限思想导入导数概念,再到导数的应用,让学生在学习数学的过程中由传统的知识理解型学习模式逐渐转变为知识应用型实践模式,推动学生创新能力的发展.
1 案例分析
导数及其应用内容在每年的全国高考数学卷中均有一道大题,分值是12 分,分数占整卷的8 %.学生作为初学者去学习这部分内容是非常困惑的,主要表现在没有记全基本初等函数的求导公式,记错乘法、除法导数运算公式,使用复合函数求导公式缺项或者多项等,即使在进行了多次的强化专项训练后,学生还是没有完全掌握导数计算的技巧.为了帮助学生掌握函数导数的求法,笔者结合教学实践对一道例题进行多种方法的求解.
已知==sincos求导函数
(一)=(sincos)=(sin)cos+sin(cos)=cos-sin
注:首先利用两个函数相乘的导数公式:[()()]=()()+()(),然后用到了两个基本初等函数的导数公式:(sin)=cos,(cos)=-sin
2 利用换元法计算导数
设=(),∈,而=(),∈,当D∩Z≠∅时,将=()代入=()中,得到=(()),称函数()和()构成复合函数(()),简记=°(),其中法则为内函数,法则为外函数,称为中间变量.

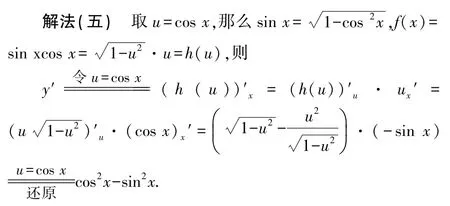
解答完毕后,与学生互动交流,要让学生得出“计算的结果一样”的结论.由具体到抽象,培养学生思维能力,如由列举的具体换元变量=2,=sin,=tan到换元=(),且不论()是关于的何种表达式,复合函数求导公式y′=y′·u′的结果是一样的.那么,需要思考如何选取简洁的、有利的、恰当的表达式(),使得计算复合函数导数的过程最为便捷.
3 选取元的原则
利用换元法是高中数学解题过程中的基本方法,同时也是学生在实际应用中的难点.在复合函数的分解过程中,选取恰当的元相当于选择恰当的中间变量.对任意的中间变量=(),总有y′=y′·u′.在利用多种方法计算导数时,要教会学生识别哪些方法是简洁的、具有优势的,特别是当出现复合函数时,需要进行由外至内的分解,找准中间变量,并落实复合函数求导公式的应用.通过布置课堂练习“例2”,让学生熟练掌握复合函数的分解要领与原则.
复合函数=lnsin由哪些基本初等函数复合而成
构造5 种分解法,具体如下:
①=lnsin=ln,其中=sin=().
②=lnsin=sin,其中=arcsin(lnsin)=().
③=lnsin=tan,其中=arctan(lnsin)=().
④=lnsin=cos,其中=arccos(lnsin)=().

让学生明白这5 种换元法从本质上看都是正确的,然而,部分方案与由繁化简才引入换元法的目的相矛盾.方案①中,变量=()=sin()是关于的1 种法则(正弦法则),在除①外的其他方案中,变量=()都是关于的3 种法则,比函数=lnsin本身的2 种法则(对数法则和正弦法则)多.函数=lnsin是关于的2 种法则,分别是先取正弦法则,再取对数法则.研究复杂的=lnsin转移到研究=(),不难发现,只有方案①具有优势(法则次数少).可以说,复合函数分解的原则是中间变量=()很容易得出,且相比函数()的运算法则少1 次(种)法则.
函数=lnsin由初等函数=ln,=sin复合而成.
注:对复合函数的分解,选取中间变量的原则就是中间变量的表达式关于变量的初等法则次数要少于分解的函数.
4 链式法则求导推广
若复合函数=()是可导的,且函数=()由=(),=(),=()初等函数复合而成,其中,为中间变量,则有链式法则求导公式
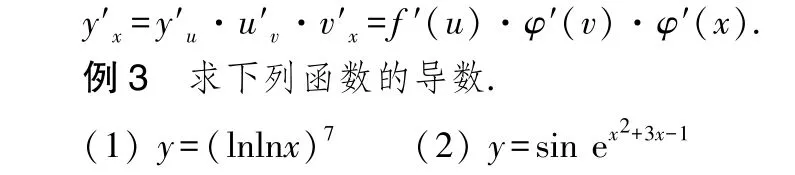
(1)函数=(lnln)由=,=ln,=ln复合而成.由链式法则可知,


5 举例应用
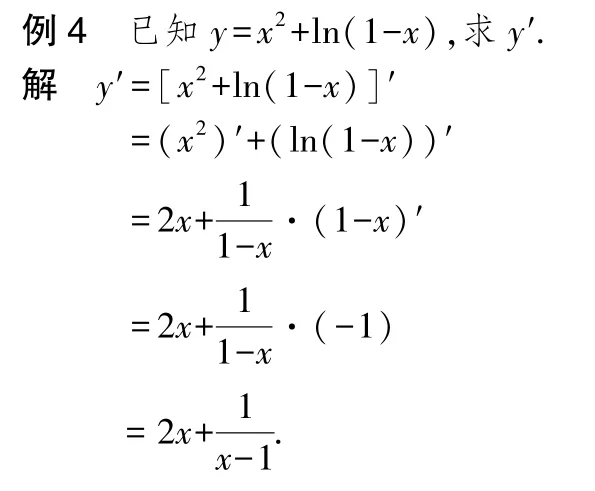
注:复合函数=ln(1-)由初等函数=ln,=1-复合而成.

6 实施有效教学监督
教学质量监控是指监控组织成员(教务处督导、同行教师、班级学生)通过对教学质量的持续监督,在分析整理教学工作质量、教学成果质量等方面信息的基础上发现可能存在的问题,对教学行为及时调控,以稳定和提高教学质量.
以复合函数求导的教学设计为例,利用两次统计检验学生对该教学内容的掌握程度.例1 讲解结束后,给出评分细则,让学生进行自我评分,然后教师统计学生得分情况,详情见表1.从统计表中,可知班级共有47 位学生,有8 位学生获得6 分,占比17.02%,12 位学生获得4 分,占比25.53%,该题满分是6 分,平均分是3.34 分,有57.447%的学生超过平均分,与教学计划中预期的平均分4 分存在一定的差距,这里就不再分析原因了.

表1 班级主观题自测评分统计表
在讲解例2 过程中,让学生选择5 种换元法中正确的数量是多少,共设4 个选项,分别是0 项、1 项、3 项和5 项,学生答题的结果详见表2.从表中看出,47 人的班级中有6 人选择正确,有41 人选错答案,选择正确的占班级人数的12.766%,平均分是0.638 分,有12.766%的人超过平均分.显然,学生对换元法的掌握不够牢固,需要加强换元法的应用,培养学生的创新能力.

表2 班级选择题评分统计表
(选择题设置的分数是5 分)
教学过程中,我们可以在例1 的解法(四)、例2 复合函数的分解方面引导学生独立思考,模仿解题思路,培养学生的创新意识,激发学生的创新性能力,把知识转化为解决问题的能力.因此,在教学中,学生对教学内容的理解情况,将会是老师进行下一步教学至关重要的信息,所以在教学中教师必须要及时利用准确的、多方位的、多角度的信息反馈,引导学生主动探究,进行教学方法、教学手段的改革.
7 小 结
本文通过课堂习题的训练,找出复合函数分解的准则,引入换元法辅助学生理解一元函数的微分不变性,并掌握复合函数的求导公式.教师应当结合布置的课后作业、习题训练,开展循序渐进的教学,巩固学生的基础知识,多留一些时间给学生思考,找规律,自我消化,让学生能够掌握数学思想方法,切不可为了完成教学进度而早早结束本节教学内容.教师应当尽可能多地对学生的作业进行批改以及检查,利用反馈信息,有针对性地调整教学计划.在数学学习、教学过程中,要重视培养学生发现问题、解决问题的能力,让学生用自己的思维,勇于解决数学问题,实现数学的应用.
