拒止场景下单无人机目标节点定位方案

董子贤, 宁 帆

(北京邮电大学 信息与通信工程学院, 北京 100876)

0 引 言

准确的位置信息在军事和民用等方面发挥着重要作用。现有的移动站辅助全球卫星导航系统GNSS(Global Navigation Satellite System)可以实现高精度定位[1-2], 但在地震、 狂风、 海啸等灾害发生时, 由于地面基站受损或卫星信号受到干扰将对定位精度造成很大影响, 甚至无法实现定位。为此, 灵活可移动、 低成本、 实时的无人机(UAV： Unmanned Aerial Vehicle)定位技术应运而生, 成为拒止环境下定位问题的研究热点[3-4]。

现有的UAV定位方法主要有3种： 基于成像模型的共线定位、 基于参考地图的定位和基于无线信号的定位。其中基于成像模型的共线定位方法利用UAV位置、 姿态角等参数对目标节点进行定位。但该方法受地形影响较大, 在地形破坏严重的灾区无法实现高精度定位[5-6]。基于参考地图的定位, 将UAV传感器采集的图像与参考地图相结合定位目标节点, 但该方案的定位精度受地图精度影响较大, 在没有明显参照物的地区定位精度将急剧下降[7-8]。基于无线信号的定位, 利用UAV与不同位置的目标节点之间的无线电传输信息进行定位, 不仅可以忽略地形的影响, 同时还具有灵活、 便捷、 实时性强的特点, 被广泛应用于拒止环境下的灾区定位[9]。

针对UAV无线定位技术, Xu等[10]提出了一种基于卡尔曼滤波的到达时间(TOA： Time Of Arrival)定位校正方法, 实现了对节点间时钟同步误差的校正。Zheng等[11]提出了一种基于加权的到达角(AOA： Angle Of Arrival)信息的室内定位方法, 该方法通过加权多个AOA信息提高定位精度。Torii等[12]提出了一种结合信号强度(RSSI： Receive Signal Strength Indication)指示器和机械学习的多点观测技术, 以实现对运动目标的跟踪和定位。Wang等[13]提出了一种基于AOA和到达时差(TDOA： Time Difference Of Arrival)的混合定位技术, 适用于远近场景的混合定位。

现有的研究多利用无人机组进行定位, 在定位过程中, 多架无人机占用大量资源, 组网过程难以控制[14]。同时多无人机之间的时钟同步误差对定位精度也有很大影响, 如何节省资源并降低时钟误差是一项重大挑战； 而在利用单无人机进行定位的研究中, 多取飞行轨迹上距离较远的等分点作为测距位置, 整个定位过程时间较长, 实时性较差。此外, 现有的基于无人机定位技术的研究主要考虑如何减小时钟同步误差以及如何对定位数据进行如卡尔曼滤波和机器学习等后续处理, 忽略了上行和下行信道之间的双向信道误差也会影响定位精度。为解决上述问题, 笔者设计了一种单无人机定位方案, 控制单无人机使其围绕以参照点为中心的固定轨迹匀速飞行, 并通过初始位置的坐标以及基于地理位置的坐标推算可以得到无人机在不同时刻的位置坐标, 取代多无人机的使用, 有效避免了多无人机之间的组网问题和时钟同步误差。针对测距过程, 在传统双向测距的基础上, 笔者提出了一种加权的双向测距方法, 并推导了双向信道误差和时钟偏移误差。与传统方法相比, 该方法可以将双向信道误差减少一半, 且对定位精度有显著提升。最后, 利用最小二乘法对多组测距信息进行解算得到目标节点相对于参考点的相对位置, 方便灾区场景下救援车对受灾人员或救援人员等目标节点的位置信息获取, 并通过仿真分析了无人机航迹高度和半径对误差的影响。

1 单无人机目标定位方案

为解决地震、 海啸等自然灾害发生后, 对救援人员和受灾人员定位难的问题, 同时为避免多无人机目标定位过程中的复杂组网和精准时钟同步需求, 笔者提出了一种单无人机定位方案, 如图1所示。

图1 无人机目标定位示意图

在目标区域以参考点, 如救援车为原点绘制空间直角坐标系, 控制无人机以坐标系原点为中心, 在固定高度绕半径为R的圆形轨迹匀速飞行,在无人机移动过程中, 采用加权双向测距(W-TWR： Weighted- Two Way Ranging)技术对无人机和目标节点之间的距离进行探测。最后, 利用无人机移动过程中的位置信息结合最小二乘法计算目标节点相对参考点的位置坐标, 实现对目标节点位置信息的获取。定位过程如下。

Step1 救援车行驶到救灾区域, 并对无人机的飞行速度以及高度和半径进行设定, 释放无人机, 使定位节点A(UAV)升空并围绕以参考点(救援车)为中心点的圆形轨迹移动。

Step2 定位节点A发送带有当前时间戳t1的无线定位信号, 并记录自身位置坐标(xi,yi,zi), 其中i为第i次测距时刻。

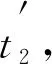
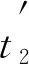
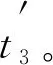
Step7 根据已知的时间信息通过加权双向测距算法计算定位节点A在起始位置与目标节点B之间的距离Si。

Step8 重复Step2～Step7的工作, 获得3组以上的坐标(xi,yi,zi)和距离数据Si, 最后利用最小二乘法求解目标节点B的坐标。

1.1 基于地理位置的UAV位置推算

在灾区拒止场景下, 无法通过GPS(Global Positioning System)等导航系统获得无人机移动过程中的位置坐标, 这将对地面目标节点的定位造成很大的阻碍。在笔者提出的方案中, 无人机相对参考点(救援车)的初始位置是已知的, 利用无人机的固定轨迹和移动特性, 可对无人机移动过程中不同时刻的坐标进行基于地理位置的推算。

如图2所示,将UAV的位置坐标投影到笛卡尔坐标系上。假设UAV在起始时刻的位置坐标为(x1,y1), 在第i次测距时刻的位置坐标为(xi,yi), 利用物理位置信息得到第i次测距位置相对于X轴的角度和(xi,yi)的位置坐标

图2 基于地理位置的位置推算模型

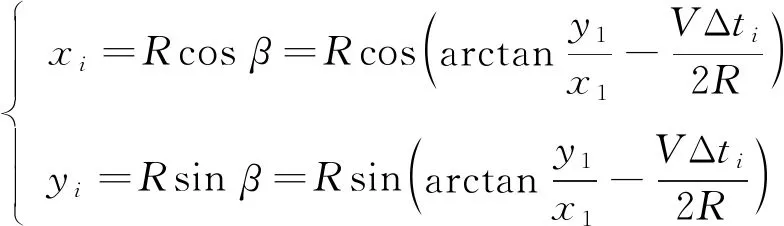
(1)

其中R为无人机飞行半径,V为飞行速度, Δti为UAV从起始位置飞行到第i次测距位置的时间间隔。θ=arctan(y1/x1)为起始位置相对水平坐标轴X的角度, 通过UAV在时间间隔Δti内绕圆飞行的弧度l, 得到第i次测距位置与起始位置的角度α=l/2R=VΔti/2R。

1.2 基于最小二乘法的目标位置解算

最小二乘法的思想是将i个坐标方程相减, 去掉未知的二次项, 将方程转化为线性方程并求解。在测距过程中, 可得到每次测距时UAV的初始位置坐标(xi,yi,zi), 以及从UAV初始位置到目标节点的无线电传输时间TTOFi(其中i=1,2,3,…, 表示第i次测距过程), 将目标节点坐标设为(x,y,z), 然后列出方程

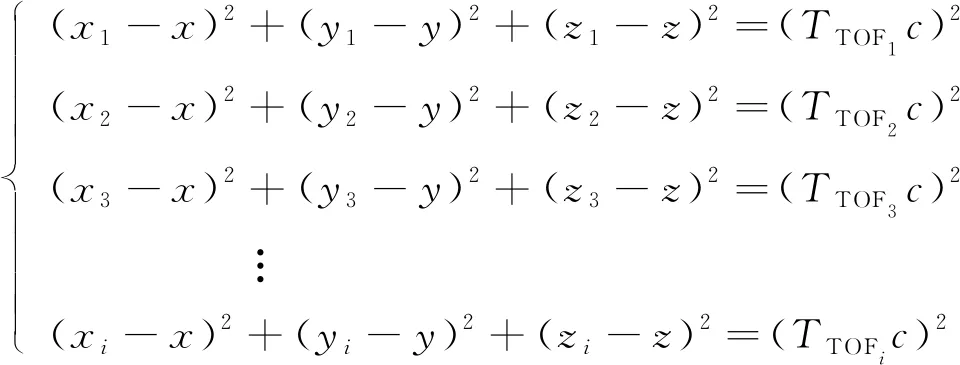
(2)

(3)

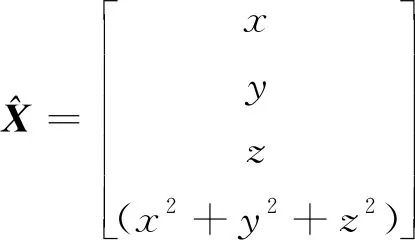
(4)

(5)

2 面向单无人机的改进测距过程

测距是无人机定位中必不可少的过程。笔者研究了双向测距技术, 并对现有测距技术进行了模型和误差分析。双向测距通过将定位节点和目标节点之间的无线信号传输时间(TOF： Time Of Fly)与信号传输速率相乘解算距离。影响测距精度的主要因素有系统延迟误差、 时钟同步误差、 时钟偏移误差以及双向信道误差[15]。为降低这些误差, 国内外学者提出了单侧双向测距(SS-TWR： Single Side Two Way Ranging)、 双侧双向测距(DS-TWR： Double Side Two Way Ranging)、 交替双侧双向测距(AltDS-TWR： Alternate Double Side Two Way Ranging)和奇数双侧双向测距(ODS-TWR： Odd Double Side Two Way Ranging)等测距方法[16]。然而, 这些方法大多面向多无人定位过程中的无人机悬停场景且只考虑了时钟偏移误差的影响, 没有考虑当无人机的移动性带来相对运动时双向信道误差也会对测距结果产生很大影响。基于此, 笔者针对单无人机定位过程提出了一种加权双向测距(W-TWR)算法, 综合考虑了双向信道误差和时钟偏移误差, 旨在提高单无人机定位过程中的测距精度和定位精度。

2.1 系统模型及误差分析

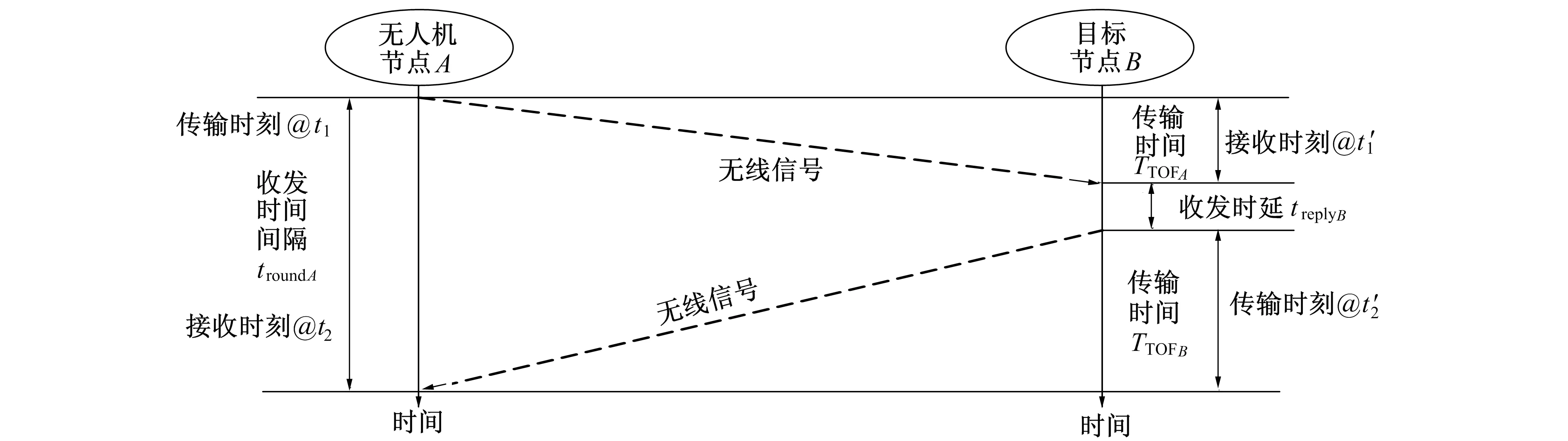
图3 测距信号传输模型

通过使用时间戳信息, 定位节点A的发送与接收信号时间间隔troundA以及目标节点B的时延treplyB为

troundA=t2-t1

(6)

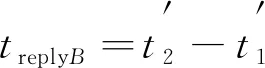
(7)

在测距过程中, 无论节点之间是否有相对运动, 都假设发送路径和接收路径相等, 因此信号的飞行时间(TTOF)为

(8)

为得到更精确的测距和定位信息, 笔者考虑了时钟偏移误差和双向信道误差对测距精度的影响, 当节点之间存在相对运动时, 无线信号在上下行信道传输的时间TTOF(A→B)和TTOF(B→A)不相等, 无人机A到目标节点B的实际飞行时间可估为

TTOF(A→B)+TTOF(B→A)=troundA-treplyB

(9)

2TTOF(A→B)+ΔT=troundA-treplyB

(10)

其中ΔT为TTOF(A→B)和TTOF(B→A)之间的时间差, 结合式(8)～式(10), 估计的传输时间和实际传输时间之间的双向信道误差e1为

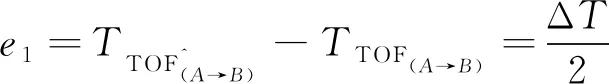
(11)

考虑到时钟偏移误差, 假设定位节点A和目标节点B相对标称时钟频率的时钟偏移分别为eA和eB。则实际传输时间为

2TTOF(A→B)=troundA(1+eA)-treplyB(1+eB)

(12)

结合式(8)～式(12), 时钟偏移误差为

2.2 加权双向测距(W-TWR)算法

针对测距过程中的时钟偏移误差和双向信道误差, 笔者提出了一种基于加权思想的测距方法。首先将传统两次测距过程变为3次, 具体测距模型如图4所示。

图4 基于加权的测距信号传输模型

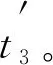
UAV的固定轨迹移动过程示意图如图5所示。A、A1和A2分别为UAVA在发送信号、 接收信号和再次发送信号时的位置, 对绕圆形轨迹移动的无人机, 它与目标节点B之间的距离遵循增大或减小或先增大后减小的趋势, 该趋势在短时间内保持不变(接近时增大, 离开时减小)。

图5 无人机轨迹趋势示意图

以图5右侧为例。SAB>SBA1>SA2B(其中S为距离), 设

(14)

其中Δ1和Δ2为上下行传输信道之间的距离差。由式(14)可得

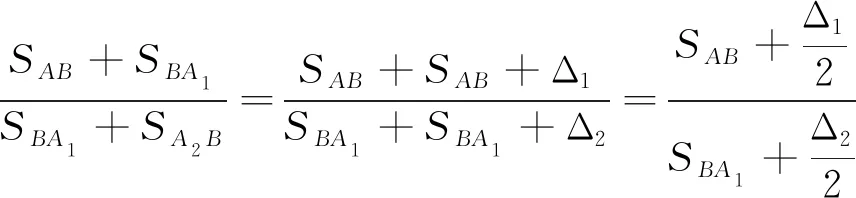
(15)

其中SAB和SBA1之和由troundB-treplyA获得,SBA1和SA2B之和由troundB-treplyA获得。treply和tround可在UAVA处或目标节点B中单独计算, 因此不需要对两节点进行同步运算, 避免了时钟同步误差。此外, 由于距离差Δ相对于距离S较小, 因此式(15)可以简化为

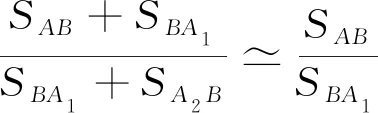
(16)

设W=SAB+SBA1/(SAB+SBA1)+(SBA1+SA2B)为TTOF(A→B)在TTOF(A→B)+TTOF(B→A1)中的权重, 则有

对双向信道误差, 设

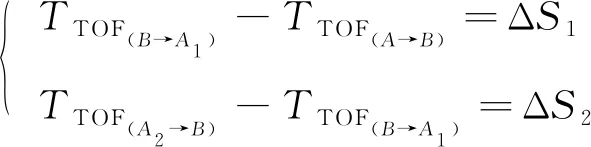
(18)

则式(17)变为

其中ΔS1和ΔS2近似相等, 且远小于TTOF(A→B)。对比式(11)与式(20)可看出, 笔者提出的加权方法可将双向信道误差降低一半以上。下面对时钟偏移误差进行分析, 用treply和tround表示信号的传输时间, 则信号传输时间TTOF(A→B)为

4TTOF(A→B)=troundA-treplyB+troundB-treplyA

(21)

当考虑时钟偏移误差时, 实际传输时间为

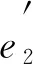
通过以上推导, 可得出结论, 笔者提出的方法可以降低时钟偏移误差, 并且与传统方法相比, 可将双向信道误差降低一半以上。对单无人机测距精度和定位精度的提高有着重要的意义。

3 仿真与分析

为验证笔者所提方案的性能, 利用Matlab对测距过程和定位过程进行仿真。

首先, 对传统方法和笔者所提方案的双向信道误差引起的测距误差进行分析。设置无人机飞行高度为200 m、 飞行半径为500 m、 无人机飞行速度为40 m/s, 在以参考点(救援车)为原点的笛卡尔坐标系上取半径为500 m的圆内随机点作为地面目标节点, 在收发时延10～90 ms的范围内对传统方法和笔者所提方案的双向信道误差引起的测距误差进行仿真, 仿真结果如图6所示。

图6 测距过程的双向信道误差分析

从图6可以看出, 基于加权的双向测距方法可将双向信道误差引起的测距误差降低至传统方案的四分之一, 且收发时延越小, 提高效果越明显。当收发时延增大时, 笔者方案的测距误差随之增大, 但仍优于传统方法。

为探讨无人机飞行高度和半径对测距定位精度的影响, 在控制其他条件与上述相同的情况下, 比较了以200 m,400 m,600 m时模拟不同高度对测距误差的影响。同时, 在相同的控制条件下, 分别以500 m,600 m,800 m为半径模拟了不同飞行半径对测距误差的影响。仿真结果如图7, 图8所示。

图7 无人机飞行高度对测距误差的影响 图8 无人机轨迹半径对测距误差的影响

从仿真结果可以看出, 当收发时延较小时, 飞行高度和飞行半径的变化对测距误差影响较小, 当收发时延增大到一定值时, 双向信道测距误差随飞行高度的增加而增大, 随飞行半径的增加而减小, 并且双向信道测距误差受无人机飞行半径的影响较之高度对其的影响更为显著。

最后, 笔者采用最小二乘法对加权测距信息进行处理, 得到目标节点的定位坐标, 并引入均方根误差(RMSE： Root Mean Squard Error)验证双向信道测距误差对定位精度的影响。RMSE的表达式如下

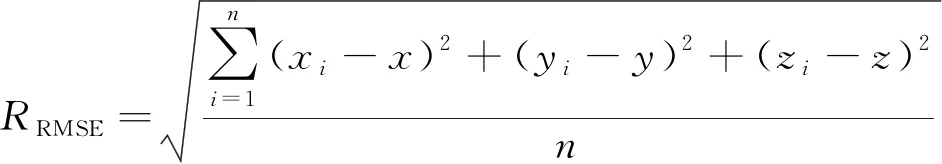
(24)

其中(x,y,z)为目标节点的真实坐标, (xi,yi,zi)为第i次定位过程的定位坐标。在模拟实验中, 设置无人机的飞行高度为400 m, 飞行半径为500 m, 飞行速度设置为40 m/s, 在以参考点(救援车)为原点的笛卡尔坐标系上取半径为500 m的圆内随机点作为地面目标节点, 在收发时延10～90 ms的围内对笔者所提方案进行仿真分析, 并利用前文提到的最小二乘法对多组测距信息进行解算, 重复试验1 000次并计算双向信道误差所带来的定位误差的RRMSE, 仿真结果如图9所示。从仿真结果可以看出, 笔者所提出的加权测距方法有效地降低了双向信道误差所带来的定位误差。

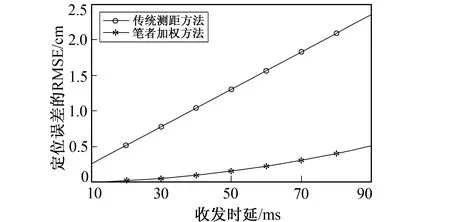
图9 定位误差RMSE比较

4 结 语

笔者提出了一种在灾区拒止场景下利用单无人机获取目标节点到参考点相对位置的灾区定位方案, 并在测距过程中提出了一种加权测距的新方法, 并通过理论推导和实验仿真对其进行了分析。实验结果表明, 笔者提出的定位方法是可行的且具有较高的定位精度, 适用于灾后拒止场景的目标节点定位。由于采用固定轨迹检测, 无人机的飞行高度及半径都会对定位结果产生影响, 因此, 对无人机轨迹参数的选取及相关理论推导将是进一步研究的重点。