分形理论与矩法估计联合的页岩孔隙结构表征

张 瑾

（中石化重庆页岩气有限公司，重庆 408400）

页岩因其发育的大量纳米级孔隙中蕴藏有丰富的天然气资源而受到广泛关注。作为一种非常规致密储层，页岩成因复杂，非均质性极强，孔喉大小达到纳米数量级，具有低孔隙度、极低渗透率等特征。大量纳米级孔隙的存在影响着页岩中油气的储集与运移［1-8］。因此，页岩孔隙结构特征研究对页岩气的评价与开发具有非常重要的意义。目前，高分辨率电子显微镜、核磁共振、小角散射、高压压汞法、气体吸附法被广泛应用到页岩孔隙结构的定性与定量表征［9］。分形维数是描述页岩孔隙结构复杂程度和非均质性的重要方法［10-14］，基于气体吸附法、压汞法、图像分析法、小角散射等数据建立分形模型，可以定量描述储层孔隙微观结构，为储层孔隙和吸附机理的研究提供新方法。

四川盆地及其周缘下志留统龙马溪组是我国页岩气勘探的重点层位之一。龙马溪组页岩有机碳含量高、热演化程度高，其孔隙结构复杂，类型多样，纳米级孔隙占主体地位，2～50 nm 的介孔平均占孔隙总体积的75.0%～83.1%，最高可达92.1%［4，15-18］。本文以龙马溪组页岩为研究对象，基于气体吸附实验，利用气体吸附分形分析方法研究页岩孔隙的分形特征，并采用矩法计算出页岩孔隙孔径均值、标准差、变异系数以及歪度等特征参数，进而分析分形维数与孔径均值、标准差、变异系数和歪度间的关系，探讨分形维数对页岩气体赋存和运移的意义。

1 方法原理

1.1 分形理论

分形理论是由Mandelbrot 在上世纪60 年代提出，自然界中极其零碎复杂，许多事物具有自相似的“层次”结构，理想情况下甚至是无穷多层次的，适合放大或缩小几何尺寸，整个结构并不改变，不少复杂物理现象的背后，是反映这类层次结构的分形几何学［19］，具有自相似性、自反演性的体系可以用分形维数来表示［20］。90年代初，国内众多学者将分形理论应用到断层活动、岩石微观断裂、固体矿床以及油气空间分布等方面的研究中［19，21-23］，分形理论是曲面粗糙度描述的最有效方法，定义为特征尺度大于r的客体数目Ni与ri之间满足幂函数关系：Ni=。

Pfeifer 等［24］利用分子吸附法证明了储集岩石的孔隙结构具有分形特征，并认为分形维数是介于2～3 之间的小数，2 表示绝对光滑表面分形维数，将极端粗糙表面的分形维数定为3。近年来，分形几何学的发展使得对复杂系统进行精确描述成为可能，为油气储层微观孔隙结构提供新的思路。众多学者利用氮气吸附分形分析方法研究了页岩孔隙结构［11，20，25-28］，发现页岩孔隙表面具有明显的分形特征，分形维数一般大于2.6，表明页岩孔隙结构复杂、非均质性较强。

基于气体吸附-解吸等温线计算固体分形维数的方法有很多，主要有粒度法、分形BET 模型法、Frenkel-Halsey-Hill 模型法（FHH）和热力学方法等［24，29-31］。其中，FHH方法适用范围较广，计算方便，应用最为广泛［11］。对在分形表面上的气体吸附，满足

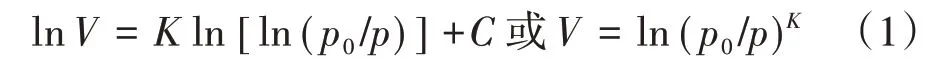
式中，V为气体吸附量，cm3/g；p为系统平衡压力，p0为吸附气体的饱和蒸汽压力，MPa；K为与吸附机理有关的常数，多层吸附时（p/p0＜0.45）为范德华力，多孔介质分形维数D=3（K+1），吸附机理为毛细凝聚时（0.45＜p/p0＜1），D=K+3；分形维数越大，材料表面越粗糙；C为常数。

由式（1），根据测得的氮气吸附等温线，在毛细凝聚区域内以lnV对ln［ln（p/p0）］作图，以最小二乘法拟合趋势线，根据曲线斜率K求得分形维数D。页岩吸附-脱附曲线分支在相对压力为0.45～1.00时出现滞后环，因此采用0.45～1.00的数据进行孔隙分形维数计算。

1.2 矩法估计理论

罗蛰潭等［32］对砂岩与碳酸盐岩进行大量研究后发现，储集岩的孔喉分布并不符合Chilingar 提出的正态分布，其孔喉分布受成岩作用及成岩后生作用影响，是多种成因造成的混合分布，所以按地质混合经验分布的数字特征，使用矩法来确定孔隙结构特征参数更为合理。王长城等［33］将矩法应用到低渗透储层孔隙结构的研究中，获取的特征参数很好地反映出储层的孔隙结构特征，表明矩法是确定低渗透储层孔隙结构特征参数的合理方法。

页岩孔隙结构复杂，以纳米级孔隙系统为主，岩性更致密，非均质性更强。沉积环境、成岩作用、岩石力学性质、构造活动等因素影响着页岩孔隙结构。矩法考虑了成岩作用及后生作用等多种地质因素对岩石孔隙结构的影响。因此，利用矩法确定页岩孔隙结构的特征参数是合理的。Li 等［9］基于矩法原理，结合氮气吸附实验，通过改进观测值分组区间划分标准，优选出可有效表征页岩孔隙结构的重要参数。

均值是位置特征参数之一，它是描述实验数据取值的平均位置。对储集岩的孔隙结构来说，表示全孔径分布的平均位置，用观测值的加权平均法得到，即

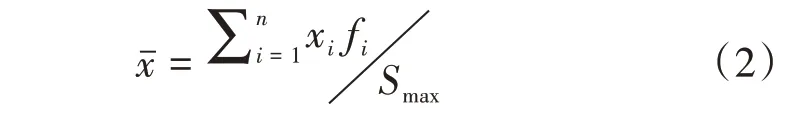
式中，xi为区间起始值（中值、末值亦可），对于储集岩来说用Φ表示，Φ值越大，孔径越小；fi为观测值（ΔSi），即液氮条件下的氮气饱和度，用百分数表示；Smax为最大进氮饱和度；n为分组数，n=15。

1.2.2 标准差（σ）

标准差属于散布特征参数，是一组数据以均值为中心的分散程度的度量，用以描述孔径大小的分选程度，亦称为孔隙的分选系数（Sp）。对于孔隙系统来说，孔隙分选越好，其分选系数越小。

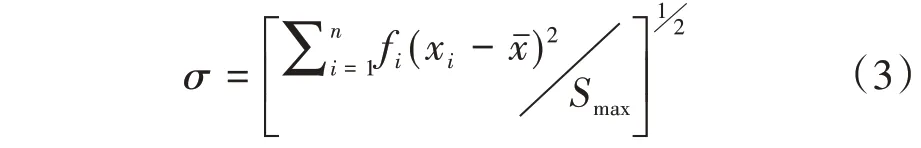
1.2.3 变异系数（c）

变异系数是标准差对平均值之比，是观测值相对变化性的一种很有用的度量，用以描述孔径均值和分选程度的比较。若孔径的平均值（Φ）越大（细孔越多）、分选越好（都是细孔），则c值越小。c值可以反映储集岩孔隙结构的好坏，一般来说，c值越大，则表示储集岩的孔隙结构越好。

1.2.4 歪度（Sk）

歪度是分布特征参数之一，它是分布不对称的测度，又可称为偏度。歪度在地质学上的含义为：孔径分布相对于平均值来说是偏大孔或偏小孔，偏大孔为粗歪度，反之为细歪度。

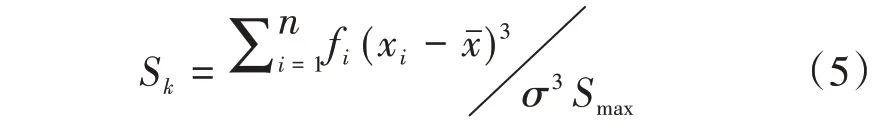
2 样品与数据处理

2.1 样品特征

为探索分形理论与矩法估计在页岩孔隙结构表征中的应用，本文选取四川盆地东南部不同区域的下志留统龙马溪组页岩样品作为研究对象。样品取自龙马溪组一段黑色页岩层系，依据X 射线衍射分析，页岩中石英含量为35%～62%，黏土矿物含量为22%～42%，碳酸盐矿物含量为5%～13%，长石含量为4%～9%，黄铁矿含量为2%～5%。根据矿物组成，本文研究样品属于硅质页岩岩相或混合质页岩岩相。

2.2 数据处理

采用美国Quantachrome 公司QUADRASORB SI比表面和孔隙度分析仪，对9 个页岩样品进行了氮气吸-脱附实验。由公式（1），根据测得的氮气吸附实验数据，在毛细凝聚区域内（p/p0= 0.45～1.00）以lnV对ln［ln（p0/p）］作图（见图1），计算分形维数（见表1）。

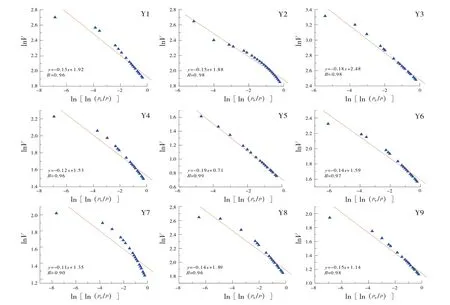
图1 页岩样品lnV与ln［ln（p0/p）］关系曲线

根据吸附等温线（见图2），采用脱附分支计算得出不同相对压力下的氮气脱附体积Vi（g），得出各相对压力下的进氮饱和度（Si）和间隔饱和度（ΔSi）；最终代入公式（2）～（5），计算得出矩法计算的页岩孔隙结构特征参数（见表1）。

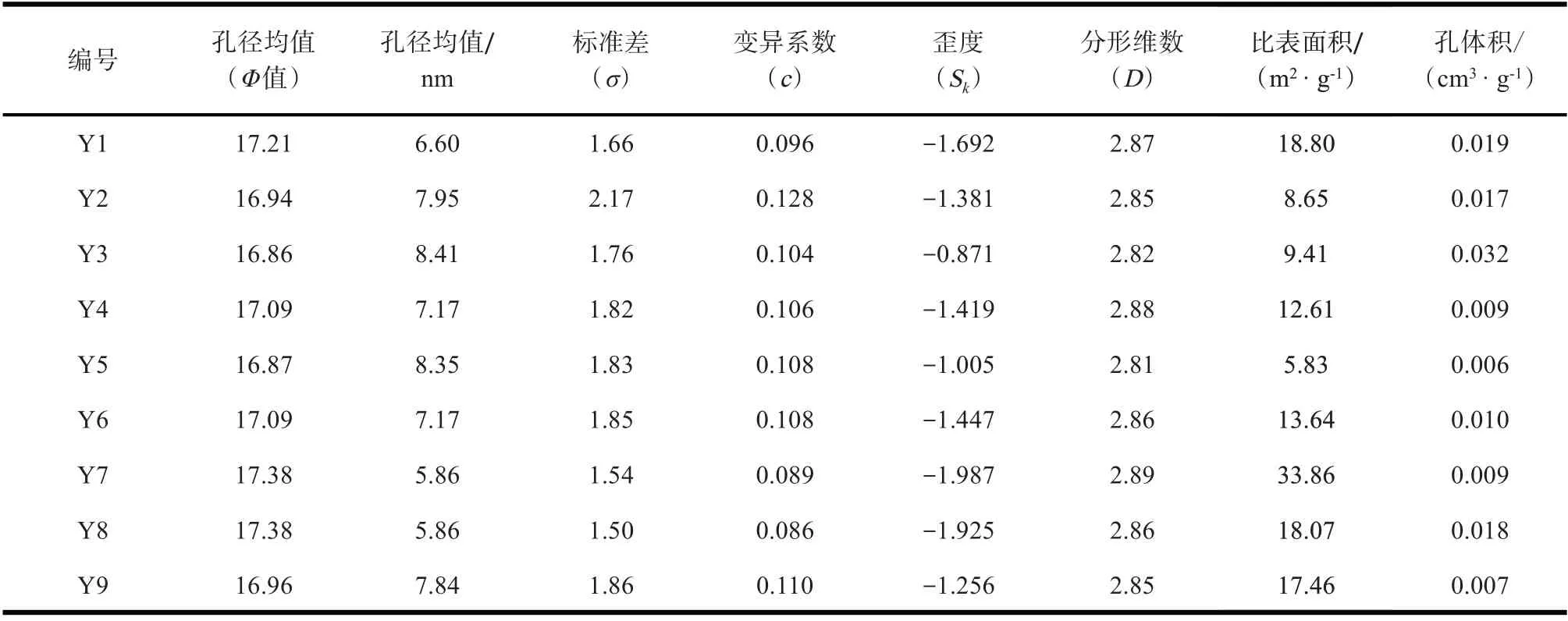
表1 页岩孔隙结构特征参数

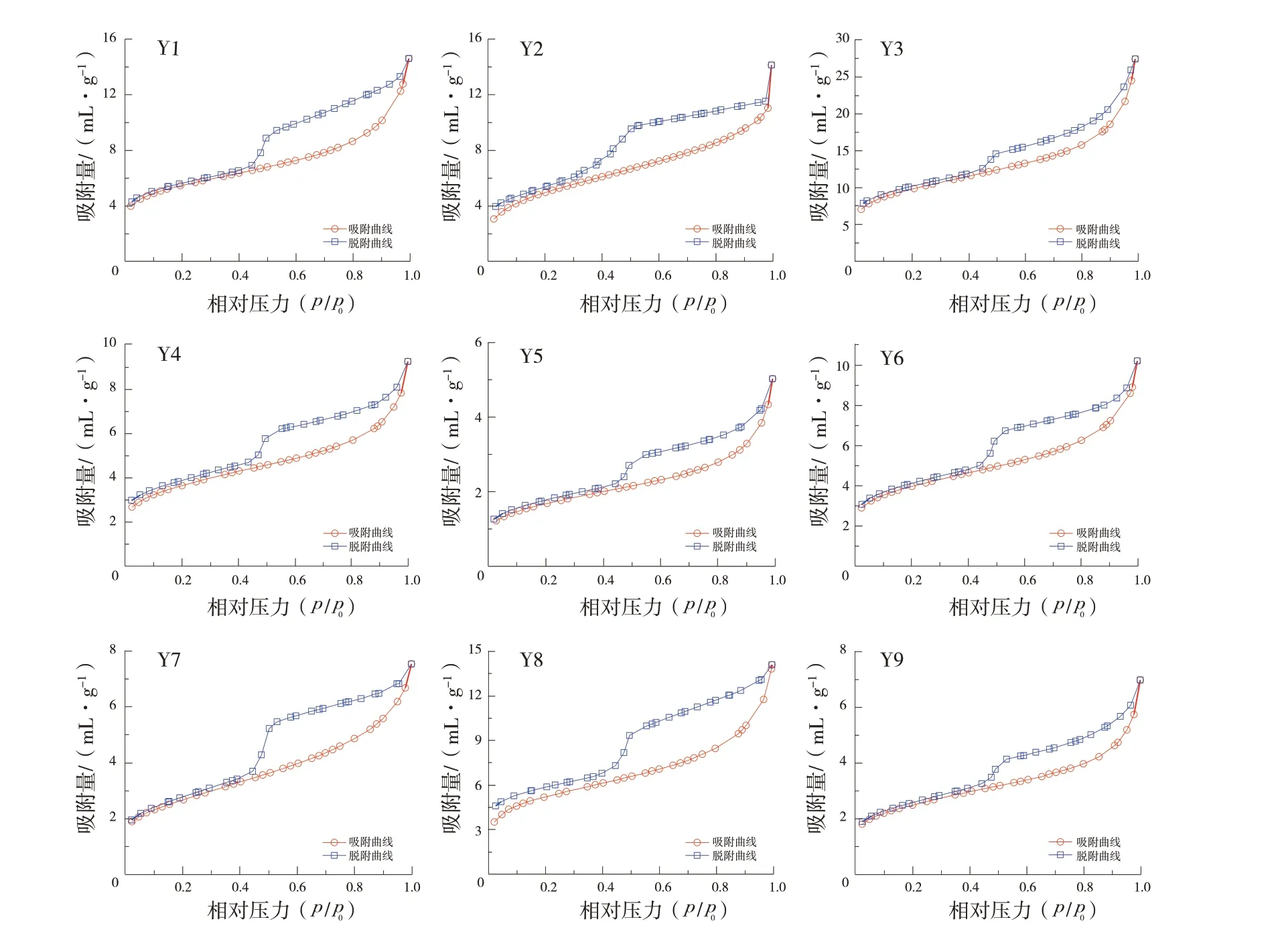
图2 页岩样品等温吸附曲线

2.3 结果

2.3.1 分形维数

由图1 可知，龙马溪页岩lnV与ln［Ln（p0/p）］数据的拟合度较好且线性相关，相关性较高，相关系数介于0.90～0.99 之间，根据分形理论，说明页岩具有明显的分形特征［19］。由式（1）计算获得的分形维数分布在2.81～2.89 的范围内（见表1），显示符合孔隙系统的分形意义（分形维数2～3）［20，24］。分形维数与页岩孔表面的不规则性和粗糙度有关，分形维数非常接近3，表明孔隙系统具有很高的复杂性，反映页岩孔隙表面不规则程度高，孔隙结构复杂，非均质性强。

2.3.2 孔隙结构特征参数

如表1 所示，9 个页岩样品的孔径均值分布在16.86～17.38φ，即5.86～8.41 nm，标准差（分选系数）分布为1.50～2.17，变异系数分布为0.086～0.128，歪度分布为-1.987～-0.871。根据BET 法计算获得的比表面积分布在5.83～33.86 m2/g，平均为15.37 m2/g；孔体积分布在0.007～0.032 cm3/g，平均为0.016 cm3/g。

根据地质混合经验分布与矩法原理，标准差（分选系数）越小，孔隙分选性越好；变异系数越大，表明孔隙间的孔径差异越大，利于油气运移，则孔隙结构越好；歪度则是孔径分布相对于平均值而言偏大孔或偏小孔的度量。矩法得出的特征参数反映出龙马溪组页岩平均孔径小，孔隙分选好，细歪度，孔隙结构较差的特征。

运用SPSS对体系中具体的7个影响因素进行相关性分析，找出影响网购客户物流配送满意度的3个显著影响因素，相关性的分析结果证明网购物流影响因素指标体系的有效性。物流配送价格、物流配送时间、物流配送完好性仍还存在很多的问题，要想改进这三个方面就需要降低物流配送服务价格、减少物流配送时间和提高物流配送商品的完好率，有利于提高网购物流配送客户满意度。

2.3.3 孔隙形态特征

等温吸附曲线的形状是孔隙形态特征的反映［35］。图2 中9 个页岩样品的吸附曲线均为反“S”形，且在相对压力接近1 时，曲线呈现继续上升趋势，没有表现出吸附限制，表明页岩中存在介孔和大孔；中压区，脱附曲线与吸附曲线不重合形成滞后回线，说明发生了毛细凝聚现象，反映平行板状的裂缝型孔、四边开口的锥形平板孔，以及细口广体的墨水瓶孔等开放性孔隙的存在；低压区，吸附曲线和脱附曲线基本重合，说明存在一端封闭的圆筒孔、锥形孔等闭合性孔隙。按IUPAC 的分类标准（见图3），龙马溪组页岩样品表现为H3 型滞后回线，并兼具H2 型特征。H2、H3 型滞后回线是无定形孔的反映，H2 型回线所反映的孔隙类型难以确定，一般认为是细口广体的墨水瓶孔，H3 型反映平行板状裂缝型孔隙［35］。

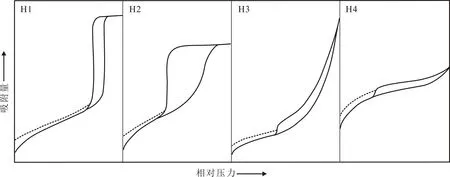
图3 IUPAC滞后回线类型［35］

根据等温吸附曲线表现出的特征，龙马溪组页岩孔隙形态复杂，以平行板状的裂缝型孔隙为主，并发育墨水瓶孔、一端封闭的圆筒孔、锥形孔等。

3 讨论

3.1 分形维数与比表面积的关系

分形维数与比表面积具有正相关关系，相关系数为0.75，即比表面积越大，分形维数也越大（见图4a）。Chalmers 等［36］发现页岩的吸附气量与微孔含量呈正相关性；Ross 等［37］对页岩的吸附实验证实了页岩对甲烷气体的吸附量随微孔含量的增加而增大。这是因为微孔提供了广大的比表面积，微孔含量越高，表面越粗糙，比表面积越大，为气体提供了更多的接触面积。气体在孔隙中的吸附过程解释了分形维数与比表面面积正相关的原因：页岩分形维数越大，吸附孔越多，吸附能力越强，有利于气体的吸附聚集。因此，分形维数可以描述微孔发育程度，反映气体吸附能力的强弱。

3.2 分形维数与孔体积的关系

如图4b 所示，分形维数与孔体积同样具有一定的负相关关系，相关系数较小（0.27），表明随着孔体积增大，分形维数具有变小的趋势。这可能是样品中孔体积主要来源于大孔的贡献，相比于微孔，大孔比表面相应减小，吸附能力降低。如Y3样品孔径均值最大（8.41 nm），歪度最大（-0.871），意味着相对于平均孔径而言，大孔所占比例相对要高，孔体积最大（0.032 cm3/g），但比表面积相对较小（9.41 m2/g），因此其分形维数较低（2.82）。

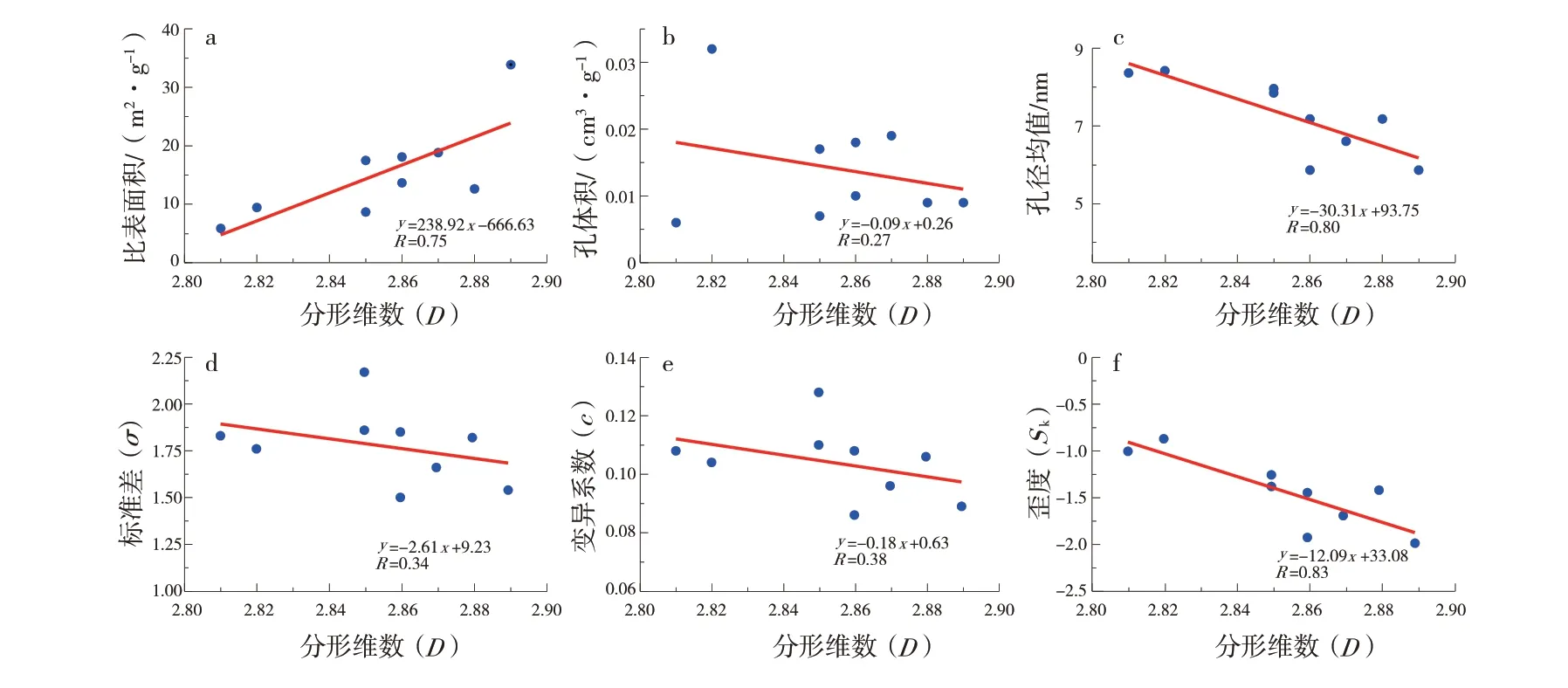
图4 分形维数与孔隙结构参数关系曲线

3.3 分形维数与孔隙形态的关系

由滞后回线类型可以看出，龙马溪组页岩孔隙形态复杂，表现为H3 型滞后回线，并兼具H2 型特征。H2 型回线一般认为是细口广体的墨水瓶孔，H3型为平行板状裂缝型孔隙［36］。H2型墨水瓶孔由于瓶颈限制，不利于吸附气体的逸散，而利于气体的保存，例如有机质中的孔隙，大孔隙可充当墨水瓶瓶体，而小孔隙充当瓶颈（见图5a）。相反，H3 型平行板状裂缝型孔隙则不利于吸附气的保存，但利于气体的运移（见图5b）。按孔隙形态特征，H2 型墨水瓶孔孔径差异大、孔隙大小不一，结构特征更为复杂（见图5a），因此分形维数应该更大。

图5 扫描电镜揭示的龙马溪组页岩主要孔隙类型

样品Y7 具有典型的H2 型特征，矩法估计揭示其具有标准差小（1.54）、变异系数小（0.089）、歪度小（-1.987）的特征（见表1），反映其孔隙结构复杂程度高；同时其分形维数最大，为2.89，同样揭示出孔隙结构最为复杂的特征。而诸如Y3、Y5 具有明显H3 型特点的孔隙，孔隙形态均一，孔径间孔径差异较小（见图5b），矩法估计揭示其标准差相对较大（1.76，1.83）、变异系数相对较大（0.104，0.108）、歪度相对较大（-0.871，-1.005）的特征，揭示其孔隙结构相对偏好，复杂程度相对变低的特性（见表1）；同时分形维数相对变小，分别为2.82，2.81，也显示了孔隙结构复杂程度变低的趋势。因此，随着孔隙形态从平行板状裂缝型孔隙向墨水瓶孔转变，分形维数变大，孔隙结构趋于复杂。

3.4 分形维数与孔径均值的关系

图4c为分形维数与孔径均值相关性分析图，从图中可以看出，分形维数与孔径均值表现出负相关的相关性，相关系数为0.80。随着孔径均值变小，分形维数变大，这是因为随着孔径均值减小，微孔所占比例越大，孔隙结构越复杂，提供的比表面积越大，导致分形维数越大；相反，由于孔径均值变大，大孔所占比例越大，孔壁粗糙度相对变小，比表面积变小，使得分形维数变小。

3.5 分形维数与孔径标准差的关系

标准差用以描述孔径大小的分选程度，对于孔隙系统来说，孔隙分选越好，其分选系数越小。由图4d 看出，分形维数与标准差呈负相关，相关系数为0.34。主要原因为标准差越小，表明微孔所占比例大，致使比表面积变大，对气体的吸附能力更强，分形维数越大。

3.6 分形维数与孔径变异系数的关系

变异系数是标准差对平均值之比，若孔径的平均值（Φ）越大（细孔越多）、分选越好（都是细孔），则c值越小，反之c值变大。若c值越大，表明孔隙间孔径均值变化大，大孔所占比例大，连通性变好，有利于孔隙流体的运移，利于油气开发，表示储集岩的孔隙结构越好。

由图4e 看出，分形维数与变异系数呈负相关，相关系数为0.38。因为变异系数越大，大孔所占比例相对提高，微孔所占比例降低，对气体的吸附减少，但孔隙连通性变好，气体可流动性变强，而孔隙结构复杂程度降低，分形维数变小。

3.7 分形维数与孔径歪度的关系

歪度反映孔径分布相对于平均值来说是偏大孔或偏小孔。由表1可知，样品歪度介于-1.987～-0.871，均表现为细歪度特征，指示相对平均值而言孔径分布更偏向于小孔。

图4f 显示分形维数与歪度之间呈负相关，相关性较高，相关系数为0.83。这是因为孔径分布相对平均值而言，若负偏程度越大，表明微孔所占比例越大，比表面积越大，对气体的吸附更多，吸附能力更强，孔隙结构更为复杂，因此分形维数越大。

4 结论

以分形理论和矩法估计为基础，结合氮气吸附实验，选取川东南地区龙马溪组页岩为对象，以FHH 模型计算出分形维数，并以矩法估计计算出孔隙结构特征参数；在此基础上，分析了分形理论与矩法估计所获参数的相关性，并探索了两种方法对页岩孔隙结构表征的适用性。研究获得以下结论：

（1）页岩分形维数与比表面积正相关，与孔体积、孔径均值、标准差、变异系数和歪度负相关。孔径均值越小，微孔所占比例越大，连通性变差（变异系数越小），孔隙结构变差，但孔内比表面积变大，对气体的吸附能力变强，分形维数变大；反之，孔隙均值越大，连通性越好（变异系数变大），孔隙结构越好，对气体的运移能力变强，分形维数变小。分形维数可以反映页岩对气体的吸附和储运能力的强弱。

（2）页岩分形维数、标准差、变异系数及歪度与孔隙形态特征表现出良好的吻合性，可作为孔隙形态的反映。H2型墨水瓶孔，由于其特殊的“瓶颈”结构利于气体吸附和保存，相应标准差、变异系数和歪度变小，而分形维数变大；H3 型平行板状裂缝型孔隙，孔隙间连通性相对较好，利于气体扩散，相应标准差、变异系数和歪度变大，而分形维数变小。

（3）矩法估计以地质混合经验分布为依据，考虑了地质系统的复杂多变性，计算出的孔径标准差、变异系数以及歪度等特征参数与分形理论和氮气吸附理论所揭示的孔隙特征具有较高吻合度。将分形理论与矩法估计联合，能拓展孔隙结构特征参数的表征方法，丰富页岩孔隙结构非均质性对比的特征参数。