复合固体推进剂高温加速试验理论与方法（1）——Arrhenius 方程的适用性

池旭辉，彭 松，赵程远，杨 根，张峰涛，曹 蓉

（航天化学动力技术重点实验室，湖北航天化学技术研究所，湖北 襄阳 441003）

0 引言

复合固体推进剂是固体火箭发动机的动力源。固体推进剂药柱在发动机工作期间要保持结构完整，对固体推进剂力学性能具有严苛要求。从配方组成上看，复合固体推进剂是一种颗粒填充的交联聚合物材料，贮存期间容易老化。老化一般会引起复合固体推进剂力学性能或其他重要性能下降，严重时导致发动机失效。因此，在发动机设计之初，就要求对复合固体推进剂的老化性能进行定量的评价，预知力学性能或其他性能的老化规律，预估其寿命终点，在失效前作出合适的应对措施，以确保武器使用的安全性和可靠性。

贮存老化贯穿固体火箭发动机整个寿命周期，是非常漫长的过程，国内外通常采用高温加速试验评估复合固体推进剂的老化性能和贮存寿命。基于高温加速试验的预估方法本质上是一种数据外推方法，外推结果的准确性严重依赖于所选用的老化动力学模型。目前复合固体推进剂老化评估广泛使用的模型是Arrhenius 方 程。但 是 近 年 来，一 些 研 究 者［1-5］对Arrhenius 方程的适用性陆续提出了疑问并尝试对该模型进行修正。我们在编写国军标《复合固体推进剂高温加速老化试验方法》（GJB10021-2021）［6］过程中，对方法相关的源流和理论基础进行了较系统的梳理，本文针对Arrhenius 方程在固体推进剂老化性能评估中的应用问题，介绍了该方程的应用现状，从理论源头分析了该方程的应用条件，指出了典型应用问题出现的原因及其解决途径，期望能进一步澄清Arrhenius方程的适用性问题的物理本源，增进行业共识。

1 Arrhenius 方程在固体推进剂贮存老化评估中的应用情况

1.1 国内应用情况

我国各类相关的温度单应力加速老化性能评估标准如表1［6-16］。表1 中，只有火药安全贮存寿命试验以及火工品71 ℃试验［9-10］采用相对保守的Berthelot 方程［9］，其他标准均采用Arrhenius 方程［10］。需要说明的是，GB/T2689.1-81《恒定应力寿命试验和加速寿命试验方法总则》［15］要求：以温度为加速应力时应力水平间隔为绝对温度倒数等间隔。这是预先假定了绝对温度倒数与速率常数的函数是线性关系，即遵循Arrhenius 方程。Arrhenius 方程对数形式如下［6］：

No.standard number standard name scope of application 12 3 4 5 6 7 8 9 1 0 GJB10021-2021［6］composite solid propellant kinetic equation Arrhenius QJ2328［7-8］composite solid propellant Arrhenius GJB770B. 506.1-2005［9］Accelerated aging test method for composite solid propellants Test method for temperature accelerated aging of composite solid propellant Test method of propellant-Prediction of safe storage life-Temperature accelerated aging method Berthelot GJB736.8-90［10］Initiating explosive device method of the test at 71 ℃GJB736.13-91［11］gun propellant ＆ DB propellant initiating explosive device with known acceleration factor initiating explosive device Modified Arrhenius（Berthelot）Arrhenius GJB92-86［12］vulcanized rubber Arrhenius GB/T 20028-2005［13］vulcanized rubber ＆ thermoplastic rubber Arrhenius GB/T 11026.1-2006［14］Method of initiating explosive device test-Accelerated life test-Method of constant temperature stress Rubber，vulcanized-Directives for determination of storage characteristics using accelerated ageing or teat air-oven method Rubber，vulcanized or thermoplastic-Estimation of life-time and maximum temperature of use from an Arrhenius plot Electrical insulating materials-Properties of thermal endurance-Part 1：Ageing procedures and evaluation of test results electrical insulating material Arrhenius JB/T 1544-99［15］Arrhenius GB/T 2689.1-81［16］Rapid heat aging test for electrical insulation impregnated paint and varnished cloth-Thermogravimetric spot-slope method Methods for constant stress and accelerated life test-Part 1：General principle electric insulating coating＆ cloth electronic component Arrhenius

式中，k为速率常数；Z 为频率因子；Ea为活化能，J·mol-1；R 为摩尔气体常数，8.314 J·K-1·mol-1；T为反应温度，K。

可见，应用Arrhenius 方程评估复合固体推进剂及高分子材料的老化性能得到国内业界广泛接受。

1.2 国外应用情况

20 世纪60 年代开始，美国固体推进剂工业界和军方开始对固体推进剂贮存性能进行系统研究。Thiokol 公 司 的Layton 和Christiansen 等［17-22］根 据HTPB 推进剂的贮存失效规律，认为老化引起推进剂基体化学结构变化是决定HTPB 推进剂贮存寿命的主要因素，提出通过高温加速老化预测长期贮存力学性能的技术途径，建立了以Arrhenius 方程为老化动力学模型的贮存寿命预估方法。但是20 世纪80 年代之后，美国军方开始对高温加速方法有疑虑，认为该方法不能正确预测固体推进剂性能的长期变化规律［23］。关于其原因，我们在后面章节中探讨。

前苏联和独联体国家一直使用以Arrhenius 方程为基础的高温加速贮存寿命预估方法。其特点之一是，严格按照Arrhenius 方程对固体发动机相关材料开展系统的试验研究，分别确定了其老化活化能分布范围［24］（表2）。对于固体推进剂，前苏联根据其老化特性分为3 类，见表3［24］。

高分子材料高温加速老化的国际标准也普遍采用Arrhenius 方程，如表1 中GB/T 20028-2005 等同采用的 国 际 标 准ISO11346-1997［25］、GB/T 11026-2006技术内容等同采用的国际标准IEC60216-1-2001［26］。

可见，固体推进剂老化性能研究方面，国际上除美国外，行业普遍认同采用Arrhenius 方程的高温加速预估方法；在高分子材料的热老化评估方面，Arrhenius方程被广泛接受。

material name gum，sealant insulation liner organic case Solid propellant aging-sensitive parameter physical property tensile strength or elongation Gas generation fracture strength-Ea/ kJ·mol-1 50-63 67-100 29-42 63-84 96-142

type Ea / kJ·mol-1 AB C aging characteristics with good chemical stability，their aging-sensitive parameters are mechanical properties（typical one is HTPB propellant）between A and C their aging-sensitive parameter is chemical stability（typical one is NEPE propellant）75-105 108-142 104-126

2 Arrhenius 方程理论来源与物理意义

Arrhenius 方程是瑞典科学家Arrhenius 根据经验总结的描述反应速率与温度关系的化学动力学公式，其一般形式和微分式分别为：

后来人们根据碰撞理论，采用统计力学的方法推导出下式［27］：

式中，Ec为阈能，是与温度无关的量；m为不大于4 的整数或半整数。双分子碰撞时，m=1/2。式（3）中ATm称为频率因子，其物理意义是单位时间发生的碰撞次数；exp（-Ec/RT）为活化因子，其物理意义是发生有效碰撞（能量大于Ec）的概率。

对 照 式（2）和 式（3），令Z=ATm，则 式（3）具 有Arrhenius 方程的形式，活化能Ea=Ec，是与温度无关的量。但是频率因子为温度相关量。

另一种处理方法是将式（3）两边取对数后对温度进行微分，有

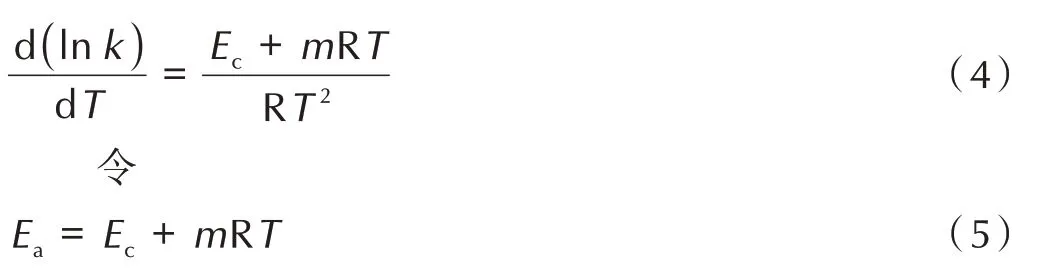
则式（3）也变换为Arrhenius 方程。此时活化能Ea是温度相关量。但频率因子Z=A，为温度无关量。

可见，根据碰撞理论，Arrhenius 方程的频率因子和活化能两个参数中有且仅有一个与温度相关。通行的做法是按照式（5），将活化能定义为温度相关的量，即每摩尔活化分子能量与每摩尔分子的平均能量之差。此时，Z 是与温度无关的常数。

然而，一般情况下mRT比Ec小得多，可以忽略不计，按照式（5）定义的活化能在实践中普遍都是作为温度无关量处理。以复合固体推进剂为例：据标准GJB10021［6］，其最高加速试验温度为80 ℃，与参比温度（一般20～25 ℃）的差ΔT不超过60 ℃，二者Ea的最大差值在0.25～2.00 kJ·mol-1之间。固体推进剂老化活化能通常在100 kJ·mol-1左右或更高（参见表2），温度的影响可以忽略。

根据上述理论分析可知：1）不宜将Arrhenius 方程的频率因子和活化能同时作为温度相关参数处理；2）不宜夸大老化活化能的温度依赖性，正常高温加速试验温度范围内，固体推进剂老化活化能可视为定值。

3 Arrhenius 方程应用的条件

3.1 老化机理一致

应用Arrhenius 方程的前提是研究所涉及的温度范围内老化机理一致。只有在足够小的温度区间内老化机理才能一致。固体推进剂老化是一个复杂的物理、化学过程，老化反应不是简单的基元反应，而是许多化学和物理变化的综合表现。可以假设，在一定的温度区间，老化反应由其中一个基元反应过程主导，即老化机理一致。这个假设，是应用高温加速外推常温老化规律的理论基础。显然，只要温度区间足够小，这个假设总可成立。问题是，只有这个温度区间足够大（不应少于40 ℃），高温外推常温才有“加速”的意义。

实践中若发现lnk-1/T曲线（Arrhenius 图）向上弯曲，首先应考虑是否存在高、低加速温度老化机理不一致的问题。长期以来，研究者［28-29］观察到多种高分子材料高温加速老化的Arrhenius 图出现弯曲。Celina［30］对这类现象进行了回顾与分析，将这类现象归结为两个独立的化学反应的作用结果：低加速温度下，活化能小的反应过程主导；高加速温度下，活化能大的反应过程主导。通过两个温度段老化速率数据，可求得转折温度。Celina 总结了几种典型的双老化反应过程材料的高、低温活化能与转折温度如表4［30］。

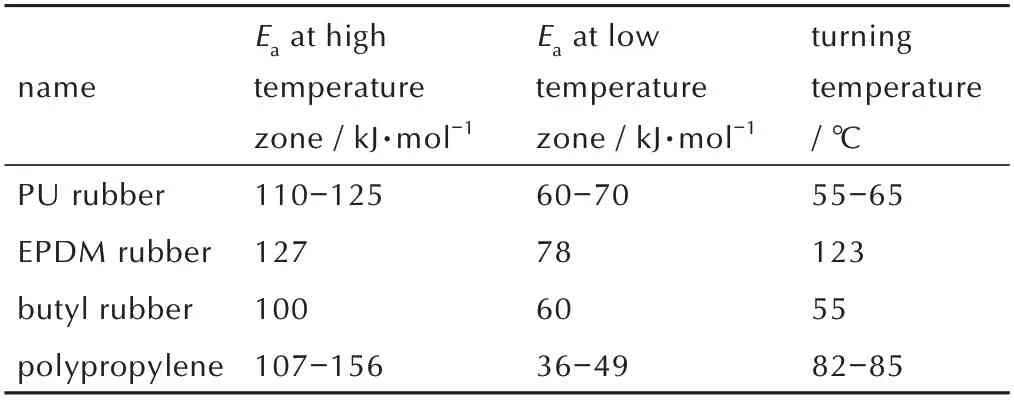
name PU rubber EPDM rubber butyl rubber polypropylene Ea at high temperature zone / kJ·mol-1 110-125 127 100 107-156 Ea at low temperature zone / kJ·mol-1 60-70 78 60 36-49 turning temperature/ ℃55-65 123 55 82-85

由表1 可见只有在不高于转折温度下开展加速老化，才能较准确地外推到常温。研究经验表明，加速温度范围过大时，固体推进剂也存在Arrhenius 图弯曲现象和老化转折温度。现行国内固体推进剂老化试验标准充分考虑了老化机理一致性问题，规定了加速老化温度范围，一般可确保不出现转折温度，即老化机理可视为一致。

3.2 老化程度相当

老化可看作一个封闭系统内的化学反应体系，这个反应体系终将趋于平衡。对于老化反应全程，性能呈现收敛函数曲线变化。一般而言，寿命周期只占整个老化进程初期的一小段（如图1）。

图1 推进剂老化进程与寿命周期的关系Fig.1 The relationship between aging process and storage life of solid propellants

图1 中不同的老化进程，性能变化规律可以用不同的数学模型：在相对全程较短的时间内，可以直线拟合；进程进一步延长，变化过程近似对数曲线。同时不同进程主导老化的基元反应也可能不同。可见，为满足性能随时间变化规律的一致性，应保证试验截止时各加速温度下老化程度相当。

由于试验进度要求的限制和认识的不足，实践中普遍存在最高加速温度过度老化，最低加速温度老化不足的问题。极端的情况是各加速温度下在同一老化时间截止，这时不同老化温度之间样品最终老化程度相差很大，很可能导致Arrhenius 图出现弯曲，数据不遵循Arrhenius 方程。

因此，应在老化程度相当的前提下，验证Arrhenius方程符合性。

3.3 速率常数应是时间的系数

性能随时间变化的数学模型决定老化速率常数。这个数学模型选择是老化预估的关键过程之一。为了数据处理方便，通常采用双参数模型，如直线模型和对数模型。Arrhenius 方程表达的是反应速率常数与温度的关系。式中k是时间的系数，即k是有量纲的，量纲包含时间倒数。

显然从理论上，拟合性能与老化时间关系的模型必须是时间系数模型，对时间取对数的模型都是不合适的。事实上，任何对时间进行变换实现线性化的操作都是违反k的定义。

由于其简单易行、经济可操作性强，是目前广大农村普遍采用的育苗方法，塑料薄膜由于能透过紫外光，昼夜温差较大，对培育壮苗有利，可防止幼苗徒长。

典型的时间对数模型如下：

式中，P为老化敏感性能参量，是老化时间t的函数；P0为P的初始值（t=0）。式（6）在QJ2328 系列标准中得到推荐，其源头可以追溯到1970 年代美国Thiokol 公司的Layton 和Lockheed 公司的Myers 等对民兵导弹固体推进剂的系列研究报告“chemical structure aging effects”和相关的推进剂老化研究报告［17-22］，这些报告都采用对时间取对数的方法处理数据。美国在80 年代之后发现高温加速预测推进剂性能变化规律严重偏离长贮监测结果，认为高温加速不能正确预测固体推进剂性能的长期变化规律（如图2）［23］。图2 老化性能预测按照时间对数曲线变化，实际监测结果基本呈线性变化。有理由怀疑，美国出现预估结果与实测结果的大幅偏离是采用时间对数模型导致的。

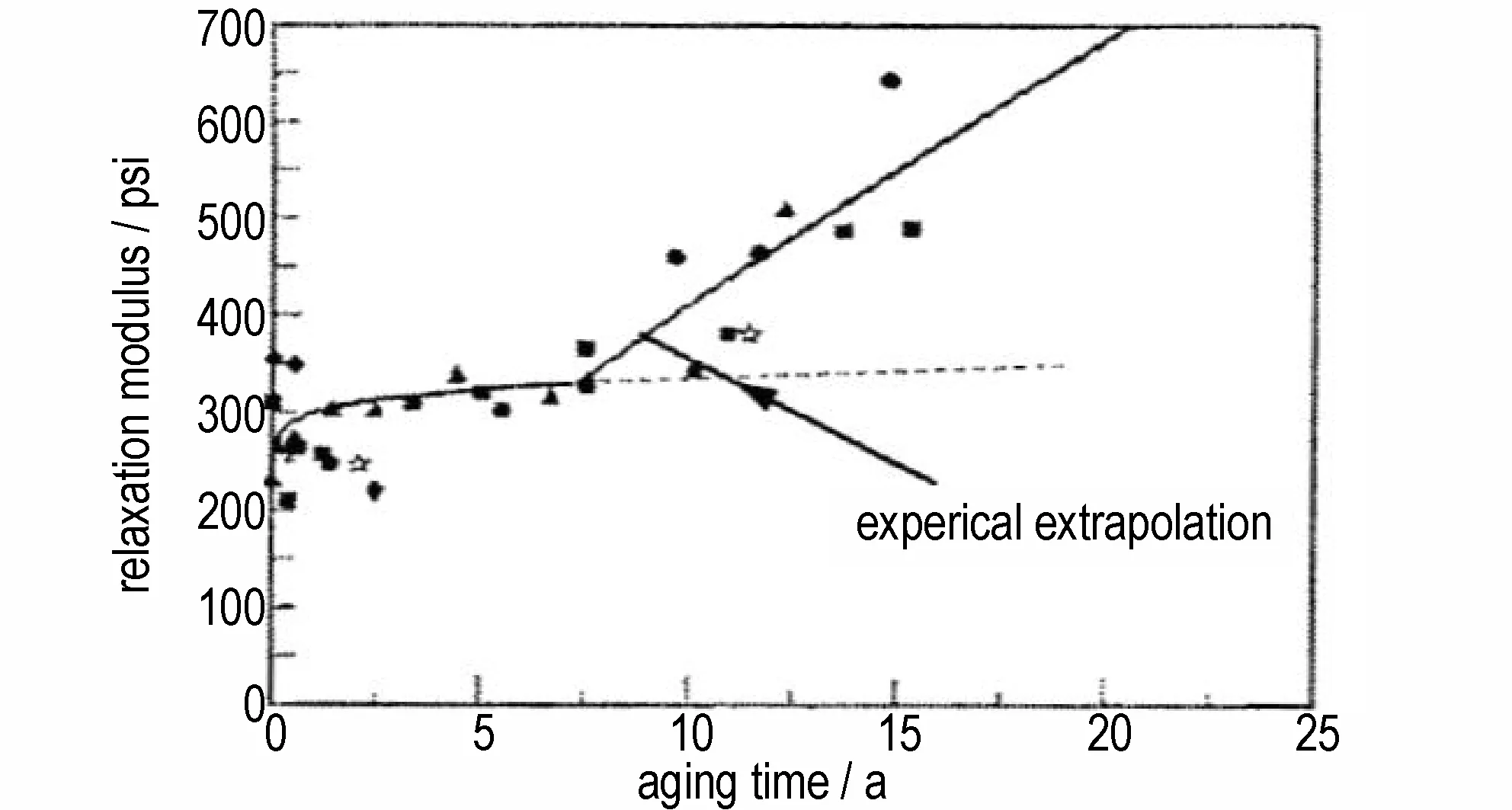
图2 美国固体推进剂老化进程与寿命周期的关系［23］Fig.2 The relationship between aging process and storage life of solid propellants made by USA［23］

4 时间对数模型在应用上的问题及替代办法

上述分析表明，时间对数模型所得老化速率常数k 不符合Arrhenius 方程中速率常数的定义，应慎重使用。人们可能有疑问，如果不考虑参数物理意义，仅用于唯象的数据拟合使用，应该不会用问题，毕竟已经使用了几十年。下面从工程应用角度，分析使用式（6）可能出现的问题。

据式（6）和式（1），求得贮存寿命τ是Ea的双重指数函数，即

其中Pf为性能失效临界值。显然，式（7）右边数值轻微的扰动，将成千上万倍放大到左边的寿命预估值，极易出现不合理的结果。

以QJ2328-92［8］附录C1 数据为例，各老化温度下最大伸长率εm监测数据如表5。按式（6）拟合表5 数据，结果如表6。

t / w 1.4 34 6 8 10 12 14 16 18 20 26 36 70 ℃35.4 33.7 34.4 30.8 33.1-32.4 40 ℃35.4 34.6 35.2 33.6 35.3 32.4 32.6---50 ℃35.4 32.5 32.2 34.1 32.0-31.5-33.1--34.4-33.0 32.5 28.0 26.4 60 ℃35.4 33.8 37.1 34.9 32.6 33.3-30.1-30.6-27.4 30.3--31.4

按照QJ2328A，以Arrhenius 方程拟合表6 数据，求得25 ℃下，εm的反应速度常数k25=0.822，k25的80%置信上限k*25=1.269。以εm下降10%（即（P0-Pf）/P0=0.10）作为失效判据，则可求得：

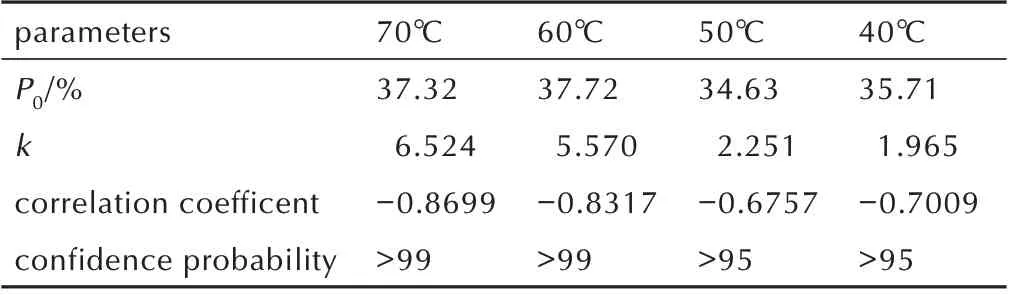
parameters P0/%k correlation coefficent confidence probability 40℃35.71 1.965-0.7009＞95 70℃37.32 6.524-0.8699＞99 60℃37.72 5.570-0.8317＞99 50℃34.63 2.251-0.6757＞95

贮 存 寿 命 预 估 值（50% 置 信 概 率）τ（10%）=103.54/0.822=20256（w）≈390（a）

二者差别超过30 倍，说明寿命分布非常分散，轻微的随机误差就可能导致预估数据的大幅变化。

进一步分析失效判据（P0-Pf）/P0对τ的影响。如图3a，logτ与（P0-Pf）/P0呈 线 性 关 系。（P0-Pf）/P0为20% 和30%时，τ（20%）和τ（30%）分别为790 万年和1600亿年，这显然违反常识。

老化活化能Ea对τ的影响如图3b（以εm下降10%为失效判据）。Ea与logτ近似线性关系。Ea增大1 kJ·mol-1，τ增大几十倍，也是不能接受的。

图3 充分表明，式（6）是不合适的。但是在高温加速寿命预估实践中，经常遇到对数曲线型数据，不能用式（6），如何处理这类数据？事实上，对数曲线型数据一般都可以对性能（纵坐标）数据取对数的方法实现良好的拟合，可称为性能对数模型。性能对数模型如下式：

式（8）的k满足速率常数的定义。此时贮存寿命

τ= ln(P0/P)/Z/exp(-Ea/RT)。

对表5 数据按式（8）拟合，结果如表7。从表7 可见，各温度下εm对数与时间t的线性相关性置信度均大于95%，满足标准要求。其中70 ℃的相关性明显优于表6，其他3 个温度略低于表6，总体上相关性基本相当。

t / w lnP0 k correlation coefficent confidence probability 70 ℃3.565 0.01106-0.9403＞99 60 ℃3.562 0.006581-0.8017＞99 50 ℃3.515 0.002782-0.6751＞95 40 ℃3.548 0.00202-0.6995＞95

根据表7，容易求得25 ℃下反应速度常数k25=0.000648，80% 置 信 概 率 下 的 上 限k*25=0.000880。以εm下降30%作为失效判据，则可求得：

贮存寿命预估值（50% 置信概率）τc=（ln35.4-ln24.8）/0.000648=549（w）≈10.6（a）

贮存寿命置信下限（80% 置信概率）τ*c=（ln35.4-ln24.8）/0.000880=404（w）≈7.8（a）

二者差别在正常范围，预估结果受误差影响较小。

失效判据与老化活化能对贮存寿命预估值的影响如图4。图4 中τ与（P0-Pf）/P0、Ea呈近似线性关系，在合理的范围内变化。可见性能对数模型是可行的。

5 结论

国内外普遍采用Arrhenius 方程处理复合固体推进剂及高分子材料的老化动力学问题。根据统计力学理论，在Arrhenius 方程形式下，频率因子和活化能两个参数之一是温度的函数。对于固体推进剂老化，现行标准允许的试验温度范围内活化能可视为定值。

应用Arrhenius 方程应符合下述条件：a）研究所涉及的温度范围内老化机理可视为一致；b）各加速试验温度下，老化程度相当；c）参数k应符合速率常数的物理意义。性能随时间变化的数学模型所得参数k不符合速率常数定义，使用应慎重，推荐使用性能对数模型替代。